Abstract
De novo protein structure prediction often generates a large population of candidates (models), and then selects near-native models through clustering. Existing structural model clustering methods are time consuming due to pairwise distance calculation between models. In this paper, we present a novel method for fast model clustering without losing the clustering accuracy. Instead of the commonly used pairwise root mean square deviation and TM-score values, we propose two new distance measures, Dscore1 and Dscore2, based on the comparison of the protein distance matrices for describing the difference and the similarity among models, respectively. The analysis indicates that both the correlation between Dscore1 and root mean square deviation and the correlation between Dscore2 and TM-score are high. Compared to the existing methods with calculation time quadratic to the number of models, our Dscore1-based clustering achieves a linearly time complexity while obtaining almost the same accuracy for near-native model selection. By using Dscore2 to select representatives of clusters, we can further improve the quality of the representatives with little increase in computing time. In addition, for large size (~500 k) models, we can give a fast data visualization based on the Dscore distribution in seconds to minutes. Our method has been implemented in a package named MUFOLD-CL, available at http://mufold.org/clustering.php.
Keywords: Bioinformatics, Distance matrix, Dscore, Near-native model selection, Protein model clustering, Visualization of distance distribution
1 Introduction
Predicting the 3D structure for a given protein amino acid sequence remains an important and challenging research topic in computational biology [1, 2]. Generally, a large number of possible conformations (referred to as models or decoys) [3–6] are typically generated in which near-native models are often contained. However, selecting the best near-native model is one bottleneck. Theoretically, the native structure of the target sequence is the conformation with minimum energy [7]. Thus, there is a popular hypothesis that near-native structures are more likely clustered in a large free-energy basin in the free-energy landscape [8, 9]. Under this hypothesis, population-based approaches are often used for near-native model selection [3,9–12].
Population-based model analysis includes clustering and representative selection for selecting and ranking the structural models. Specifically, clustering methods group models into different clusters based on structural similarities, while the representative selections typically take the centers of the clusters (representatives) as the candidates of near-native structures and ranks the candidates according to cluster sizes. There are three major issues involved in such a population-based approach: (i) measure of structural distance; (ii) use of distance information for clustering; and (iii) selection of a cluster representative.
There are a number of methods to measure the structural distance/similarity [13], such as RMSD (root mean square deviation) [14], MaxSub score [15], Global distance test total score [16], and TM-score (template modeling score) [17]. For all of these measures, transformation and optimization are needed, and different pairs of models have different transformations. For optimization, RMSD minimizes structural difference while the other measures maximize structural similarity between models. In this process, structural similarity maximization is much more computationally expensive than RMSD minimization, although the similarity measures are often more useful to describe the relationship between models than RMSD. To save computing time, RMSD is the most widely used in protein structure clustering [9, 11, 12, 18–22] during both cluster determination and representative selection.
Most algorithms for model clustering are based on pairwise C-alpha-atom RMSD distance (pRMSD). All pRMSD-based methods [9, 11, 12] are time and space expensive because the clustering requires N(N-1)/2 RMSD calculations and storage for N models, where N is often on the order of 105 or higher. Some methods were proposed to reduce the number of pRMSD calculations. For example, Calibur [18] uses auxiliary groups with upper and lower bounds and only the pRMSDs among the members in the same group need to be calculated; Durandal [19] estimates pRMSD of (B, C) by the known pRMSDs of (A, B) and (A, C); ONION [20] estimates approximate centers via random samplings and only the RMSDs of models to the estimated centers need to be computed; SCUD [21] proposes a reference RMSD distance to mimic RMSD, i.e. to orientate all of the models to a randomly selected model (named reference), and to calculate pRMSD directly without further translation and rotation; Pleiades [22] uses 31-dimensional Gauss integral vectors [23] to represent protein's 3D structure and perform K-means clustering on these Gauss integral vectors. All these studies made some progress in improving the clustering efficiency, but there is still significant room to speed up the clustering, as we will demonstrate in this paper.
In this work, we propose a novel approach for much faster structural model analysis than existing methods without loss of clustering accuracy [26]. At first, we propose two new measures, identified as Dscore1 and Dscore2, to describe the difference (mimicking RMSD) and the similarity (mimicking TM-score) of two models by a direct distance matrix comparison without using an optimized superimposition search. Both Dscores1 and Dscore2 have good mathematical attributes, leading to a much lower computational complexity and faster computing for large-scale structural clustering and representative selection. Second, different from the common strategy that calculates the pRMSD (or reference RMSD) at first and then conducts clustering our method detects the potential cluster centers from the distribution of Dscore1 and constructs the clusters from the potential centers directly. This method avoids the costly pairwise distance calculation and speeds up the clustering dramatically. Furthermore, instead of using the structural difference of RMSD for selecting structural representative, we take advantage of the structural similarity score, i.e. TM-score mimic, Dscore2 to obtain better representatives. We can obtain comparable clustering and representative selection performance to existing pRMSD methods while taking only a fraction of the computational resource of pRMSD methods. In addition, for large number (>105) of models, MUFOLD_CL still works well and we also can provide a fast data visualization based on the Dscore distribution.
2 Materials and methods
2.1 Data sets
We have two data sets. One is a benchmark that has been used to evaluate clustering and near-native selection performance by existing tools [18–20, 22], i.e. the dataset published on I-TASSER's website, which includes 12 500–32 000 models per protein for 56 nonhomologous proteins (http://zhanglab.ccmb.med.umich.edu/models/model1.html). The other one is to show our performance and visualization on larger-scale data, including 500 000 Rosetta models per protein for two proteins (http://mufold.org/clustering.php). We refer these two data sets as I-TASSER models and Rosetta models in the following.
2.2 Dscore1 and Dscore2
Both Dscore1 and Dscore2 are based on a distance matrix, which contains the pairwise C-alpha distance of a model. The distance matrix is a 2D representation of a 3D structure; it is independent of the coordinate system and contains sufficient information to reconstruct the 3D structure except for overall chirality [24]. We further apply a 1D form, distance vector, to represent distance matrix for convenience.
Given a model of a protein with L residues, its distance vector is defined as D = [dij] = [d11, d12, . . . , d1L, . . . , dij, . . . , dLL], where dij is the Euclidean distance of the i-th and j-th C-alpha atoms of the model. Dscore1 of two models with distance vector of D1 and D2 is defined as
| (1) |
where ∥D1D∥ and ∥D2∥ are the norms of D1 and D2. We normalize to D/∥D∥ and citeD/∥D∥ as D in the following for convenience. Note that Dscore1 between any two models is in the range of [0, 1]. The Dscore2 of two models is defined as
| (2) |
where the functional form is similar to TM-score [17] andd0is also defined as that described in TM-score, i.e. . Note that when the distance vector is normalized by d0asD = [dij], 1 ≤ i, j ≤ L, then we have the simplified formulation of
| (3) |
Although for a given residue pair <i, j>, dij = dji, we can simplify the calculation of Dscore1 and Dscore2, we still keep the definitions for better understanding.
2.3 Mathematical properties of Dscore1
Both centroid and medoid reflect the center of a cluster, i.e. the point whose average dissimilarity to all members in the cluster is the minimum (or the average similarity to all members is the maximum). Mediod is required to be one member of a cluster while centroid is not. In practice, medoid is more useful in model selection than centroid since a centroid may not be protein like. Medoid may not be the one closest to the centroid in general, especially for RMSD, TM-score, and global distance test total score measures. However, for Dscore1, the medoid of a cluster is the one closest to the centroid, as proved in the following.
Given a cluster of structural models, C = [1], where D is the normalized distance vectors of model, if we consider the minimum Dscore1 square, the centroid of C is , where ∥C∥ represents the number of models in C. This can be proved in the following equation. The average Dscore1 square of any distance vector X to all the members in C is
| (4) |
Since is a constant, reaches the maximum and the average Dscore1 square reaches the minimum in Eq (4). when . It indicates , i.e. is the centroid of the cluster C. In addition, the average Dscore1 square of any D in C to all the members in the C is
| (5) |
which indicates that , i.e., the one closest to the centroid is the medoid of the cluster.
We note the normalized centroid as the centroid in the following, i.e. . Given any D in C, the projection of D on is . The difference of the projections of models D1 and D2 on is , thus,
| (6) |
For any D in C, we have∥D∥2 = dot(D, D) = 1, thus,
Thus, Dscore (D1, D2)
| (7) |
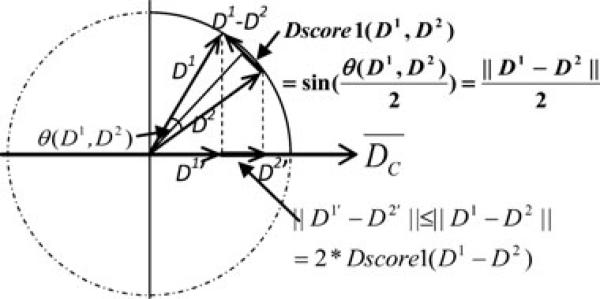
From Eqs. (6) and (7), we obtain that ∥D1’ – D2’ ≤ 2 * Dscore1 (D1, D2), which means the difference between the projections of two models on the centroid is no more than two times of their Dscore1 distance, which is illustrated in Fig. 1. This property provides a basis for a projection-based clustering depicted in the following subsection.
Figure 1.
A schematic illustration of the relationship between Dscore1 value of two models (D1 and D2) and their projection difference on the centroid. Here, Dscore1 (D1, D2) (shown by bold solid oblique line) equals to the half chordal length between D1 and D2. The projection difference between D1 and D2 (shown by bold solid line) is no more than 2 * Dscore1 (D1, D2). Although this graph is a 2D illustration, the relationships represented in the graph hold true for high-dimensional space.
2.4 Projection-based clustering
Instead of the commonly applied strategy that calculates the pairwise distances at first and then performs clustering, our preferred clustering method is to project the models onto the Dscore1 centroid to estimate the potential representatives and then cluster the models by their distances to the estimated representatives.
Specifically, given two models D1 and D2 with small RMSD, RMSD(D1, D2) < δ1, then Dscore1 (D1, D2) < δ2 where δ2 is probably a small value also since Dscore1 is highly correlated with RMSD for small RMSD values; thus, the difference of the projections of D1 and D2 onto centroid is less than 2 * δ2. This means that the models in a cluster (with small RMSD distances) typically have clustered projections on , showing that the distribution of can be used to guide the clustering. However, the opposite is not true, i.e. models with close projections onto may not have small RMSD value. Therefore, we can start clustering by finding the candidate clusters of the projections then apply a filtering process to remove outlier models.
An intuitive way of clustering from the distribution of is to treat the centroid of the whole dataset as a reference to estimate the centroid of the biggest cluster. However, since two models far from each other in terms of RMSD may have similar Dscore1 values to , centroid estimated based on Dscore1 alone may not work well. To address this issue, an iterative purifying and expanding strategy is applied: at first a reference (the estimated center of a cluster) is calculated through those models with similar Dscore1 values to centroid and then the models close to the reference will be collected to a cluster. The algorithm is depicted as follows (an illustration flowchart can be found in Supporting Information Fig. 1):
Input: The model pool P including N models of one protein, and CL = {φ}
Calculate , and obtain . calculate the distribution of DscoreSet
Calculate a Mixture Gaussian fitting for DscoreSet, and determine the best number of Gaussians by Schwarz criterion [25], which takes into account both the data fitting and the number of parameters used in the fitting. Choose the Gaussian fitting N(μ, σ2) with the smallest μ value. // According to the definition of Dscore1, we know that the smaller the Dscore1 value, the closer the two models are. Here, we choose the Gaussian fitting with the smallest μ value, which means that we choose those models that are closest to the center for estimating the potential reference model of the dataset.
Collect .
Calculate , and . to obtain the estimated reference.
C = {D|D ∈ P – C L, Dscore1(D, Dref) < 2σ} is the newly obtained cluster, and is the representative of the cluster C. // to build new cluster according to Dref.
C L = C L υ C, go to step (i) till P – C L ϕ.
Output: the sorted representatives according to the cluster sizes.
In steps (i) and (ii), the Gaussian fitting N(μ, σ2) of Dscore1 to the centroid of the dataset provides a raw bound of the largest cluster, and based on this fitting a purified subset is obtained. In step (iii), Dset1 includes models close to the center of the Gaussian distribution, which is assumed to be close to the center of the biggest cluster. Then Dset2 is calculated to exclude models that are not close to the center of the cluster. Finally, a reference is calculated as the centroid of Dset2, and a cluster is obtained by collecting models close to the reference. The models in the current detected cluster are removed from the model pool and the clustering process is applied on the remaining models until there is no model left. Since we just compare the models to the estimated reference, the clustering time is linear to the number of models. Considered the Dscore1 calculation and the comparison between the models and the estimated reference, the computational complexity is O(N * L2), where N is the number of the models and L is the number of residues of the protein.
2.5 Dscore2 and representative selection
Dscore2 is designed to describe the structural similarity of two models based on their distance matrices. Given a cluster including N models, C = {Dk, 1 ≤ k ≤ N}, the centroid under Dscore2 maximizes its average similarity to the members in the cluster, i.e.
| (8) |
Specifically, . Thus, we have
| (9) |
It means that we can calculate the centroid by calculating xij, 1 ≤ i, j ≤ L independently.
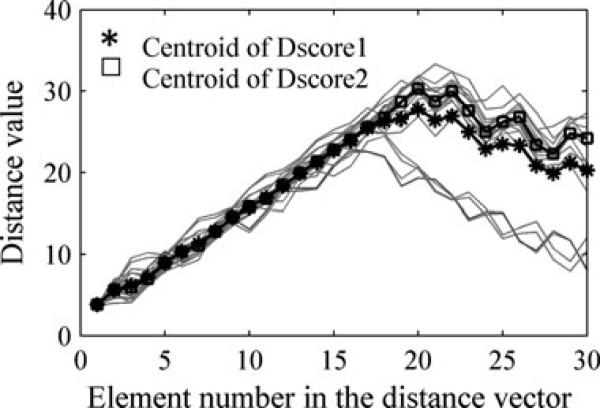
As we have discussed in Subsection 2.3, the centroid of a cluster under Dscore1, , is a mean value of the distance vectors in the cluster. When the data is divergent, the mean value does not reflect the center of the data well. Figure 2 illustrates the difference of centroid vectors defined by Dscore1 and Dscore2. When the values of one element distribute narrowly, the centroids defined by Dscore1 and Dscore2 are very close. However, when the values of one element distribute divergently, the centroid defined by Dscore2 reflects the data center much better than the one by Dscore1. Thus, we apply Dscore2 rather than Dscore1 for representative selection.
Figure 2.
An example to show the difference of the centroids defined by Dscore1 and Dscore2.
The one closest to centroid may not be the medoid of Dscore2 for an arbitrary dataset. However, when the dataset is distributed narrowly, the one closest to the centroid is more likely to be the medoid. We tested on a nonredundant subset of I-TASSER models (http://zhanglab.ccmb.med.umich.edu/models/model2.html, where each set includes 300–500 models). In 4 of 56 (7.1%) subsets, the one closest to the centroid is not the medoid. We also tested on clusters of I-TASSER models in which models of each target were clustered up to 20 clusters and the clusters were ranked according to their sizes. In general bigger clusters have tighter distributions, and bigger clusters are typically used in near-native model selection in practice. In total, there are 354 clusters for 56 targets in which 22 models (6.2%) closest to the centroids are not medoids (details are shown in Supporting Information Table 1). The average violation rate is similar to that in the above nonredundant subset. However, there is only one violation out of 56 No. 1 clusters and three violations in total out of 168 top-3 clusters (1.8%), while the remaining 19 violations come from the other 186 smaller clusters (10.2%), showing much less violation rate for bigger (tighter) clusters. Considering the low computational cost to calculate the centroid and the low violation rate on big clusters, we select the one closest to the centroid as the representative of the cluster although it may not always be the exact medoid.
3 Results
Dscore1 and Dscore2 are designed to mimic RMSD and TM-score, respectively. We calculated the correlation coefficients of Dscore1/RMSD and Dscore2/TM-score on randomly selected 500 I-TASSER models for each protein (details are shown in Supporting Information Table 2). The average values for all data from 56 proteins are 0.9226 (Pearson) and 0.8922 (Spearman). The low correlation is mostly attributed to cases with large RMSD. When RMSD ≤ 4Å, the Pearson/Spearman correlation coefficients are 0.9490/0.9305, showing a significantly higher correlation for small RMSD values [26]. Since only models with small RMSD values are expected to be clustered, this provides a basis for replacing RMSD with Dscore1 in clustering. Similarly, Dscore2 has a very high correlation coefficient with large TM-score. Such a high correlation between Dscore2 and TM-score provides a basis for replacing TM-score with Dscore2 in structural representative selection (an example of linear fittings of Dscore1/RMSD and Dscore2/TM-score can be found in Supporting Information Fig. 2).
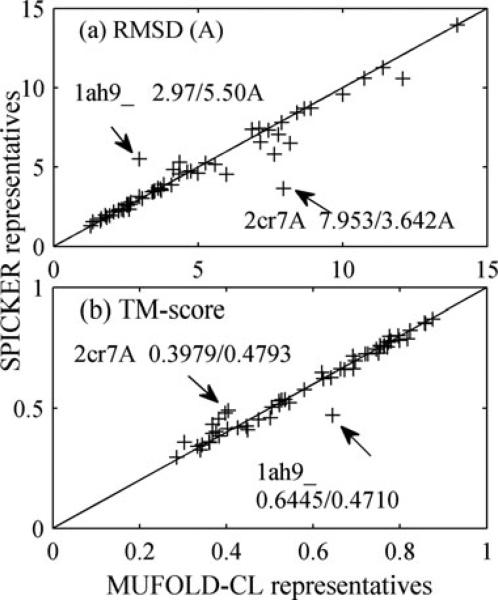
We implemented our new method in a software package MUFOLD-CL, which is available at http://mufold.org/clustering.php. To evaluate performance of MUFOLD-CL, we compared it with SPICKER [12], Calibur [18], ONION [20], and Pleiades [22] in terms of the CPU time and the quality of representatives. At first, we applied Dscore1 for both clustering determination and representative selection. Figure 3 shows the comparison with SPICKER (details of this comparison can be found in Supporting Information Table 3).
Figure 3.
Comparison between MUFOLD-CL and SPICKER by their representatives of the largest clusters in terms of RMSD (a) and TM-score (b) to the native structures for 56 proteins.
For proteins with more than 20 000 models, we cite the RMSD/TM-score of the SPICKER representatives from I-TASSER's website since SPICKER failed to calculate clusters on our computers. For proteins with 20 000 or fewer models, the average computing time (excluding the file processing for both tools) of MUFOLD-CL is 11.73 s, 60 times faster than 727.44 s of SPICKER on average. As the number of models increases, MUFOLD-CL would be much faster than SPICKER since the computing time of MUFOLD-CL is linear to the number of models while SPICKER is quadratic. More importantly, MUFOLD-CL has similar accuracies for the top-1 near-native model selection to SPICKER: 4.94Å versus 4.84Å in RMSD and 0.5910 versus 0.5911 in TM-score on average [26]. We can observe some outliers in Fig. 3; for example, the representatives of 1ah9_ and 2cr7A. For 2cr7A, the two top clusters of MUFOLD-CL have comparable sizes, and the corresponding representatives have RMSD/TM-score to the native structure of 7.95Å/0.3979 and 3.59Å/0.4793, respectively. The two top representatives of SPICKER have RMSD/TM-score of 3.64Å/0.4793 and 7.70Å/0.3392. The situation for protein 1ah9_ is similar to that of 2cr7A, indicating that overall SPICKER and MUFOLD-CL conduct the clustering and select representatives similarly. We also compared the best representatives from the top-3 clusters (details of this comparison can be found in Supporting Information Table 4). The average RMSD/TM-score of representatives of MUFOLD-CL and SPICKER are 4.44Å/0.6023 and 4.59Å/0.5910, respectively, showing a slightly better of representative selection of MUFOLD-CL.
Among the 56 target proteins, seven proteins have more than 20 000 models for which SPICKER failed to report the results. Calibur [18] claimed that it was 4/3 times faster than SPICKER, and Pleiades showed around two times faster than Calibur while Pleiades had a similar accuracy to Calibur [22]. We compared MUFOLD-CL with Calibur on these data as shown in Table 1. We found 88 to 270 (152 on average) times speedup of MUFOLD-CL over Calibur for these cases [26]. In addition, MUFOLD-CL is significantly better than Calibur, thus, much faster and better than Pleiades also, in the quality of selected models, with 3.36Å versus 4.12Å in RMSD and 0.6903 versus 0.6530 in TM-score on average, respectively [26].
Table 1.
Performance comparison between MUFOLD-CL and Calibur on seven large model sets
| Protein | # of models | CPU time (s) |
RMSD to native (Å) |
TM-score to native |
|||
|---|---|---|---|---|---|---|---|
| MUFOLD-CL | Calibur | MUFOLD-CL | Calibur | MUFOLD-CL | Calibur | ||
| 1ah9_ | 27498 | 12.70 | 1125.38 | 2.97 | 3.31 | 0.6445 | 0.6450 |
| 1aoy_ | 32000 | 14.30 | 3144.66 | 4.75 | 4.72 | 0.6727 | 0.6649 |
| 1cy5A | 32000 | 28.40 | 3585.62 | 1.63 | 1.62 | 0.876 | 0.8701 |
| 1gpt_ | 32000 | 7.76 | 1384.36 | 4.37 | 6.29 | 0.5213 | 0.5113 |
| 1tfi_ | 32000 | 7.82 | 2111.49 | 4.99 | 7.87 | 0.5224 | 0.3084 |
| 1thx_ | 32000 | 47.80 | 3939.86 | 2.26 | 2.26 | 0.7966 | 0.7966 |
| 2a0b_ | 32000 | 39.00 | 3804.93 | 2.54 | 2.78 | 0.7989 | 0.7745 |
| Average | 22.53 | 2728.04 | 3.36 | 4.12 | 0.6903 | 0.6530 | |
Among the 56 proteins in the test set, there are many “easy” cases, for which most models are very similar to the native there is one dominant model cluster. Hence, all clustering methods obtain very similar clustering and representative selection results. There are also nine “hard” proteins with less than 20 000 models each, for which the models are much more divergent, and more clusters with comparable sizes exist. We compared the best representatives of the top-5 clusters in term of RMSD obtained by different methods (details of the comparison can be found in Supporting Information Table 5). The average RMSDs of MUFOLD-CL, SPICKER, Pleiades, and Calibur representatives are 5.90Å, 6.43Å, 6.92Å, and 6.95Å, respectively, indicating that MUFOLD-CL performs the best. We also compared MUFOLD-CL with ONION on these nine “hard” proteins (details of the comparison can be found in Supporting Information Table 6). MUFOLD-CL obtained slightly worse representatives than ONION, with average TM-score of 0.3764 versus 0.3822 to the native structure. However, compared to MUFOLD-CL, ONION reported too many clusters (average of 52 of ONION versus 12 of MUFOLD-CL). In addition, MUFOLD-CL used a total of 236.14 s for the nine targets CPU time (including 126.24 s for file processing and 109.90 s for clustering and representative selection), while ONION used a total of 1228.71 s [20], which indicates that MUFOLD-CL is much faster than ONION on clustering and selection.
We also applied Dscore2 for representative selection after we obtained the clusters by using Dscore1 (a detailed comparison in terms of the quality of representative selection by Dscore1 and Dscore2 can be found in Supporting Information Table 7). Dscore1 has an average performance of 4.94Å/0.5910 (RMSD/TM-score) for the representative selection. After we applied Dscore2 on the same clusters, the performance was improved to 4.89Å/0.5939, while Dscore2 did not increase the computing time much. It is obviously that for those proteins with narrowly distributed models, there is basically no room for improvement in the clustering and representative selection. In fact, for 28 of 56 proteins, there is no improvement in TM-score by applying Dscore2. There are 18 improved cases with a total of 0.3265 point TM-score gain, while ten cases become worse with a total of 0.1618-point loss in TM-score. The average TM-score of 0.5939 by MUFOLD-CL is even better than 0.5911 by SPICKER, although MUFOLD-CL is substantially faster.
The above used distance vector in Dscore1 and Dscore2 includes all pairwise residue distances of a model, i.e. L(L-1)/2 distances for a protein with L residues, which are highly redundant. It is estimated that only a small portion of these distances are needed to describe the structure [27, 28]. For large-scale datasets, such as the Rosetta models including 500 000 structural models each for two protein 1aoy_ (with 68 amino acids) and 1abv_ (with 103 amino acids), we randomly selected one-tenth of all pairwise residue distances as the distance vector and did the same clustering and selection process. For data of 1aoy_, it took MUFOLD_CL 457.03 s for loading the data into the program while only 43.92 s for clustering; For models of 1abv_, it took 767.37 s for data loading while 206.51 s for clustering (details of the clustering results can be found in Supporting Information Table 8). The structural models of 1aoy_ are clustered into 14 clusters in which there are four dominant clusters. The best representative of the four clusters has 0.7612 TM-score and is 2.099Å to native; it is even better than the best of the 32 000 I-TASSER models, which has 0.7330/2.410Å, respectively. It means that we can benefit from sampling a larger number of models and selecting the good models very quickly by MUFOLD-CL. The data of 1abv_ are clustered to 22 clusters in which there are two large clusters and 20 other clusters with similar sizes. The best representative of the two large clusters and the best of the total 22 representatives have 0.4873 and 0.5097 TM-scores to the native, respectively, while the best of the 12 500 I-TASSER model has 0.5090 TM-score. The top-1 model selected by SPICKER has only 0.2955 TM-score.
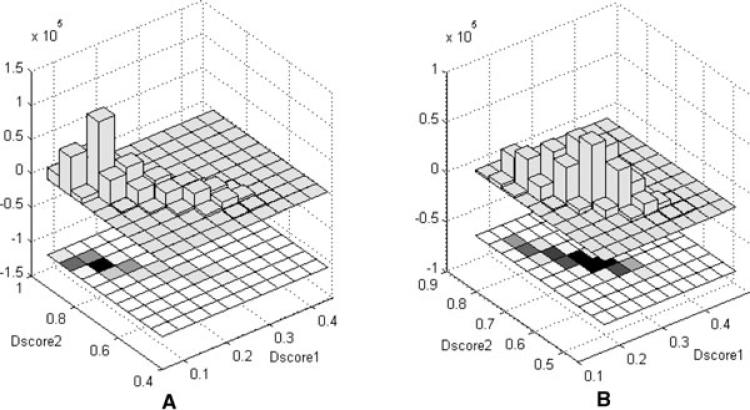
In addition, we can visualize the model distribution by their Dscore distribution in seconds to minutes for 500 k models. As mentioned in subsections of 2.3 and 2.5, the centroids under Dscore1 and Dscore2 can be treated as the centers of the data. We calculate and plot Dscores of all models to these two kinds of centers for the Rosetta models in Fig. 4. Since the smaller of Dscore1 and the larger of Dscore2, the closer of two models are, we can see that the models of 1aoy_ in Fig. 4 distribute narrowly around the centers while the models of 1abv_ distribute much divergently. As a consequently, the models of 1aoy_are clustered to less number of clusters than the models of 1abv_.
Figure 4.
Dscore1 and Dscore2 of all models to the centroids of the dataset under Dscore1 and Dscore2 measures, respectively; (A) distribution of 1aoy_ models and (B) distribution of 1abv_ models. The bottom part of the figure shows the 2D projected view of the data intensities, the darker, the denser. The upper part of the figure shows the histogram of the data.
4 Discussion
This paper has introduced two new measures, Dscore1 and Dscore2, based on the distance matrix comparison of the structures. Dscore1 is highly correlated with RMSD and Dscore2 is highly correlated with TM-score, while both scores have good mathematical properties that enable us to avoid the time-consuming structure superimposition in RMSD/TM-score calculation. More importantly, under the Dscore1 measure, the centroid of a cluster represents the center of the cluster, making it possible to detect the potential cluster representatives from the distribution of Dscore1's projection to the centroid of the dataset and construct the clusters from the potential representatives accordingly. In this way, we avoid the costly pairwise distance calculation and speed up the clustering dramatically. By using Dscore2 to select representatives of clusters, we can further improve the quality of the representatives to the native structure. Test results indicate that our method is much faster than the existing methods while achieving comparable accuracy. This method may also be adapted for other problems, e.g. small molecule structure clustering, clustering 3D objects, etc. [29].
Although distance matrix contains sufficient information to reconstruct the 3D structure, it cannot tell the chirality of structure model, since the model and its mirror share the same distance matrix. Because Dscore1 and Dscore2 are based on distance matrix, a model and its mirror have the same Dscore1 or Dscore2. This is not the case for RMSD and TM-score. Although in practice, one model and its mirror rarely exist as valid models in the same pool; nevertheless, we still need to address this issue in the future. In addition, since the all-pairwise residue distances for a given protein are highly redundant, we need to improve the efficiency of MUFOLD-CL further. We are designing algorithms to optimally select a subset of distance vector elements that can reflect the distance matrix without significant information loss. In this way, we can further decrease the computing time and memory space dramatically using reduced Dscore1 and Dscore2.
Supplementary Material
Acknowledgments
This work has been supported by National Institutes of Health Grants R21/R33-GM078601 and R01-GM100701. Major computing time was provided by the University of Missouri Bioinformatics Consortium.
Abbreviations
- pRMSD
pairwise RMSD
- RMSD
root mean square deviation
- TM-score
template modeling score
Footnotes
Additional supporting information may be found in the online version of this article at the publisher's web-site
The authors have declared no conflict of interest.
References
- 1.Baker D, Sali A. Protein structure prediction and structural genomics. Science. 2001;294:93–96. doi: 10.1126/science.1065659. [DOI] [PubMed] [Google Scholar]
- 2.Floudas CA. Computational methods in protein structure prediction. Biotechnol. Bioeng. 2007;97:207–213. doi: 10.1002/bit.21411. [DOI] [PubMed] [Google Scholar]
- 3.Simons KT, Kooperberg C, Huang E, Baker D. Assembly of protein tertiary structures from fragments with similar local sequences using simulated annealing and Bayesian scoring functions. J. Mol. Biol. 1997;268:209–225. doi: 10.1006/jmbi.1997.0959. [DOI] [PubMed] [Google Scholar]
- 4.Wu S, Skolnick J, Zhang Y. Ab initio modeling of small proteins by iterative TASSER simulations. BMC Biol. 2007;5:17. doi: 10.1186/1741-7007-5-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hamelryck T, Kent JT, Krogh A. Sampling realistic protein conformations using local structural bias. PLoS Comput. Biol. 2006;2:e131. doi: 10.1371/journal.pcbi.0020131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bystroff C, Shao Y. Fully automated ab initio protein structure prediction using I-SITES, HMMSTR and ROSETTA. Bioinformatics. 2002;18(Suppl 1):S54–S61. doi: 10.1093/bioinformatics/18.suppl_1.s54. [DOI] [PubMed] [Google Scholar]
- 7.Go N, Taketomi H. Respective roles of short- and long-range interactions in protein folding. Proc. Natl. Acad. Sci. USA. 1978;75:559–563. doi: 10.1073/pnas.75.2.559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dobson CM, Šali A, Karplus M. Protein folding: a perspective from theory and experiment. Angew. Chem. Int. Ed. 1998;37:868–893. doi: 10.1002/(SICI)1521-3773(19980420)37:7<868::AID-ANIE868>3.0.CO;2-H. [DOI] [PubMed] [Google Scholar]
- 9.Shortle D, Simons KT, Baker D. Clustering of low-energy conformations near the native structures of small proteins. Proc. Natl. Acad. Sci. USA. 1998;95:11158–11162. doi: 10.1073/pnas.95.19.11158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Roy A, Kucukural A, Zhang Y. I-TASSER: a unified platform for automated protein structure and function prediction. Nat. Protocols. 2010;5:725–738. doi: 10.1038/nprot.2010.5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Betancourt MR, Skolnick J. Finding the needle in a haystack: educing native folds from ambiguous ab initio protein structure predictions. J. Comput. Chem. 2001;22:339–353. [Google Scholar]
- 12.Zhang Y, Skolnick J. SPICKER: a clustering approach to identify near-native protein folds. J. Comput. Chem. 2004;25:865–871. doi: 10.1002/jcc.20011. [DOI] [PubMed] [Google Scholar]
- 13.Koehl P. Protein structure similarities. Curr. Opin. Struct. Biol. 2001;11:348–353. doi: 10.1016/s0959-440x(00)00214-1. [DOI] [PubMed] [Google Scholar]
- 14.Kabsch W. A solution for the best rotation to relate two sets of vectors. Acta Crystallogr. A. 1976;32:922–923. [Google Scholar]
- 15.Siew N, Elofsson A, Rychlewski L, Fischer D. Max-Sub: an automated measure for the assessment of protein structure prediction quality. Bioinformatics. 2000;16:776–785. doi: 10.1093/bioinformatics/16.9.776. [DOI] [PubMed] [Google Scholar]
- 16.Zemla A. LGA: a method for finding 3D similarities in protein structures. Nucleic Acids Res. 2003;31:3370–3374. doi: 10.1093/nar/gkg571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhang Y, Skolnick J. Scoring function for automated assessment of protein structure template quality. Proteins. 2004;57:702–710. doi: 10.1002/prot.20264. [DOI] [PubMed] [Google Scholar]
- 18.Li SC, Ng YK. Calibur: a tool for clustering large numbers of protein decoys. BMC Bioinformatics. 2010;11:25. doi: 10.1186/1471-2105-11-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Berenger F, Zhou Y, Shrestha R, Zhang KY. Entropy-accelerated exact clustering of protein decoys. Bioinformatics. 2011;27:939–945. doi: 10.1093/bioinformatics/btr072. [DOI] [PubMed] [Google Scholar]
- 20.Li SC, Bu D, Li M. Clustering 100,000 protein structure decoys in minutes. IEEE/ACM Trans. Comput. Biol. Bioinform. 2012;9:765–773. doi: 10.1109/TCBB.2011.142. [DOI] [PubMed] [Google Scholar]
- 21.Li H, Zhou Y. SCUD: fast structure clustering of decoys using reference state to remove overall rotation. J. Comput. Chem. 2005;26:1189–1192. doi: 10.1002/jcc.20251. [DOI] [PubMed] [Google Scholar]
- 22.Harder T, Borg M, Boomsma W, Rogen P, Hamelryck T. Fast large-scale clustering of protein structures using Gauss integrals. Bioinformatics. 2012;28:510–515. doi: 10.1093/bioinformatics/btr692. [DOI] [PubMed] [Google Scholar]
- 23.Rogen P, Bohr H. A new family of global protein shape descriptors. Math. Biosci. 2003;182:167–181. doi: 10.1016/s0025-5564(02)00216-x. [DOI] [PubMed] [Google Scholar]
- 24.Holm L, Sander C. Protein structure comparison by alignment of distance matrices. J. Mol. Biol. 1993;233:123–138. doi: 10.1006/jmbi.1993.1489. [DOI] [PubMed] [Google Scholar]
- 25.Schwarz G. Estimating the dimension of a model. Ann. Statist. 1978;6:461–464. [Google Scholar]
- 26.Zhang J, Xu D. Fast algorithm for clustering a large number of protein structural decoys. Bioinformatics and Biomedicine (BIBM), 2011 IEEE International Conference on 2011. :30–36. [Google Scholar]
- 27.Clore GM, Robien MA, Gronenborn AM. Exploring the limits of precision and accuracy of protein structures determined by nuclear magnetic resonance spectroscopy. J. Mol. Biol. 1993;231:82–102. doi: 10.1006/jmbi.1993.1259. [DOI] [PubMed] [Google Scholar]
- 28.Doreleijers JF, Raves ML, Rullmann T, Kaptein R. Completeness of NOEs in protein structure: a statistical analysis of NMR. J. Biomol. NMR. 1999;14:123–132. doi: 10.1023/a:1008335423527. [DOI] [PubMed] [Google Scholar]
- 29.Gorgan D, Bartha A, Truta A, Stefanut T. Information Technology and Applications in Biomedicine, 2009; ITAB 2009. 9th International Conference on.2009. pp. 1–4. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.