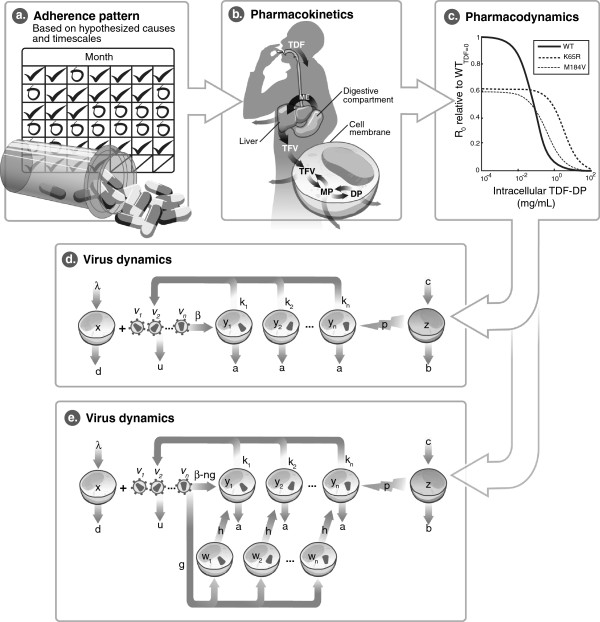
Figure 1.

Model schematic. (a) The model first assumes an adherence pattern, which is translated into a series of taken or missed doses over time. Doses, if taken, are assumed to be taken at a specified interval, e.g., daily for TDF. (b) A pharmacokinetic model of TDF translates the series of doses into a time-varying concentration of TDF-DP in the active intracellular compartment. By including the longer half-life of intracellular TDF-DP compared to TFV, this model captures the “pharmacologically forgiving” properties of TDF. (c) The relationship between the TDF-DP concentration and the replication of WT or mutant virus is assumed to be a Hill function following the median-effect model. WT is better able to replicate in the absence of drug, whereas the drug-resistant mutants are able to replicate at higher drug concentrations. K65R has higher fitness than M184V at all drug concentrations, and thus is expected to predominate over M184V in all simulations. (d) The basic virus dynamics model, governed by Equations 2–5, is depicted graphically. The additional factors of forward- and back-mutation due to error in reverse transcription, not depicted here, are shown in Equations 6–7. (e) The expanded virus dynamics model, which includes a latently infected cell compartment w, is depicted here and in Equations 11–12.