Understanding the Structural Ensembles of a Highly Extended Disordered Protein

Abstract

Developing a comprehensive description of the equilibrium structural ensembles for intrinsically disordered proteins (IDPs) is essential to understanding their function. The p53 transactivation domain (p53TAD) is an IDP that interacts with multiple protein partners and contains numerous phosphorylation sites. Multiple techniques were used to investigate the equilibrium structural ensemble of p53TAD in its native and chemically unfolded states. The results from these experiments show that the native state of p53TAD has dimensions similar to a classical random coil while the chemically unfolded state is more extended. To investigate the molecular properties responsible for this behavior, a novel algorithm that generates diverse and unbiased structural ensembles of IDPs was developed. This algorithm was used to generate a large pool of plausible p53TAD structures that were reweighted to identify a subset of structures with the best fit to small angle X-ray scattering data. High weight structures in the native state ensemble show features that are localized to protein binding sites and regions with high proline content. The features localized to the protein binding sites are mostly eliminated in the chemically unfolded ensemble; while, the regions with high proline content remain relatively unaffected. Data from NMR experiments support these results, showing that residues from the protein binding sites experience larger environmental changes upon unfolding by urea than regions with high proline content. This behavior is consistent with the urea-induced exposure of nonpolar and aromatic side-chains in the protein binding sites that are partially excluded from solvent in the native state ensemble.

Introduction

It is well established that intrinsically disordered proteins (IDPs) have fewer stabilizing intramolecular interactions and are more dynamic than ordered proteins.^1–13 This is because they do not contain a high enough fraction of nonpolar residues to form a hydrophobic core.^4,5,14,15 However, many IDPs do exhibit some degree of collapse relative to a classical random coil and in general IDPs have a broader range of compactness as a function of polymer length when compared to chemically unfolded proteins.^4,16 It is necessary to understand the forces responsible for this behavior before a comprehensive picture of the ensemble structure of IDPs can be developed.

A random polymer model has been successfully used to describe the hydrodynamic dimensions of chemically unfolded proteins that are ordered in their native state.^17–21 A simple power law relationship can be used to predict the radius of gyration (R_g) for such proteins based solely on polymer length.^17,18 There is a growing consensus that this model cannot be accurately applied to IDPs because of the obvious compositional and physicochemical differences between the chemically unfolded states of ordered proteins and the native states of IDPs. For instance, IDPs generally have a higher net charge and proline content than most ordered proteins and it is likely that these differences will play a prominent role in defining their hydrodynamic dimensions. This was recently investigated by Forman-Kay and colleagues where they showed that accounting for proline content and overall net charge improved the prediction of the hydrodynamic dimensions for IDPs.¹⁶ When these attributes are taken into account many IDPs are more compact than expected for a classical random coil.

If IDPs are not random coils then what are they? Several groups have used a variety of techniques to investigate the structural ensembles of IDPs but a general approach to characterize and classify these structural ensembles has not emerged.^3,10,22–32 Only a handful of IDP structural ensembles have been determined so it is too early to tell if they are providing a robust and realistic representation of the equilibrium ensemble. However, there are some notable features that the experimentally determined structural ensembles of some IDPs share. For instance, short segments of transient helical secondary structure are commonly observed, and these short helical segments often correspond to protein binding sites.^9,33–35 Transient long-range contacts have also been observed for a few IDPs.^{24,31,32,36,37}

Most investigations of IDP structural ensembles rely heavily on nuclear magnetic resonance (NMR) spectroscopy because of its ability to provide atomic level information on IDP structure and dynamics. Small angle x-ray scattering (SAXS) is also an important tool because it provides a comprehensive, low-resolution picture of the equilibrium ensemble. SAXS is also the premiere solution state tool for investigating protein compactness. Defining the degree of compactness for IDPs is an important step that can be taken to understand their equilibrium structural ensembles. In particular, understanding how the relative compactness of an IDP is affected by chemical denaturants will help identify the forces that contribute to their marginal stability.

The transactivation domain of the tumor suppressor protein, p53, was selected as a disordered model system for this study. Residues 1–73 of p53 form a transactivation domain (p53TAD) that is responsible for regulating its transcriptional activity and cellular stability.^38–40 This domain contains binding sites for the ubiquitin ligase, MDM2, and the 70 kDa subunit of replication protein A, RPA70. This domain also contains thirteen prolines and has a net negative charge of −14e. When bound to MDM2, p53 becomes ubiquinated and targeted for proteosome-mediated degradation. When bound to RPA70, p53 may be stabilized and available to amplify the cellular response to DNA damage.⁴¹ Several studies have shown that human p53TAD is intrinsically disordered but there is no consensus description of its equilibrium structural ensemble.^{31,32,41–45} One model of the p53TAD structural ensemble was based on distance restraints from paramagnetic relaxation enhancement (PRE) experiments and another was based on a combination of SAXS data and angular restraints from residual dipolar coupling (RDC) experiments^31,32,45. The model based on the PRE restraints was probably more compact than the true equilibrium ensemble but it did reliably identify an interesting asymmetry in the distribution of negative charge that helped rationalize the recruitment of basic factors to the site of transcription. The model based on SAXS and RDC restraints was less compact than the PRE model but the backbone dihedral angles of the structures in that ensemble were biased toward values observed in the coil and loop regions of ordered proteins.

In this study, SAXS, size exclusion chromatography (SEC), and dynamic light scattering (DLS) were used to show that the radius of gyration and the hydrodynamic radius of p53TAD significantly increase when the protein is chemically unfolded with urea. This increase in the hydrodynamic dimensions of chemically unfolded p53TAD means that the native state of p53TAD has an inherent degree of compactness that is disrupted in the presence of urea. This hypotheses is supported by results from a new protocol we developed to generate structural ensembles of IDPs. Structures with the largest contribution to fitting the SAXS data show persistent features in the native state of p53TAD that are eliminated in the unfolded state.

Materials and Methods

Preparation of p53TAD samples

Samples of p53TAD, residues 1–73 of human p53 with the R72 polymorphism (molecular mass 8205 Da), were prepared as previously described.⁴¹ In summary, a pET28a clone containing the cDNA for p53TAD was overexpressed in Escherichia coli BL21(DE3) cells for six hours. The cells were pelleted, resuspended in a buffer containing protease inhibitors, and lysed using a French press. The clarified lysate was loaded onto a column containing Ni-NTA Superflow resin and eluted with a buffer containing 300 mM imidazole. Fractions containing p53TAD were combined and dialyzed into a buffer suitable for SEC. The Histidine tag was cleaved using thrombin and the solution was loaded onto a HiLoad 16/60 Superdex 75 prep grade column (Pharmacia, 17 1068-01). The p53TAD protein was eluted at a flow rate of 1.0 ml/min. The fractions containing p53TAD were pooled, dialyzed into an appropriate buffer for SAXS, SEC, or DLS, and concentrated to 2–10 mg/ml.

SAXS measurements of p53TAD

SAXS experiments were performed on ID02 beamline at ESRF synchrotron, Grenoble, France, as previously described.⁴⁶ The sample-to-detector distance was set at 1.5 m, and the wavelength (λ) at 1.0 Å, giving access to scattering vectors q ranging from 0.018 to 0.39 Å⁻¹, where q = 4πsinθ/λ, and θ is the scattering angle. Ten successive frames of 0.5 seconds were collected for each sample. Between each frame the protein solution was circulated through an evacuated quartz capillary. Measurements on the buffer solution at the same urea concentration as the protein were performed before and after each protein sample.

The individual frames were averaged if no radiation damage or bubble formation was observed. The buffer signal was then subtracted from the protein scattering curves after proper normalization and correction from detector response. All the experiments were conducted at 20°C. SAXS data was collected on p53TAD samples at 4 mg/ml and at 10 mg/ml, in the presence of 0, 2, 4, 6, and 8 M urea. The initial buffer solution was 50 mM NaH₂PO₄ (pH 6.5), 50 mM NaCl, 1 mM EDTA, 0.02% NaN₃. Data at 4 mg/ml protein and 4 M urea had to be discarded because of the presence of a bubble in the capillary during data acquisition.

The R_g was inferred for p53TAD, at all protein and urea concentrations, from the Guinier law, in the appropriate q-range (qR_g ≤ 1) : I(q) = I(0) exp(−q² R_g²/3), where I(q) is the scattering intensity and I(0) is the forward scattering intensity⁴⁷. The 4 mg/ml data was used for subsequent analysis because it was less affected by interparticle repulsion. The distance distribution function P(r) was calculated from the scattered intensity by indirect Fourier-transform using the program GNOM.⁴⁸

The SAXS data for p53TAD was also modeled as a Kratky-Porod chain, using the following relationship⁴⁹:

$$\text{I}(\text{q})/\text{I}(0)=2/x^2(x-1+{\text{e}}^{-x})+b/L[4/15+7/15x-(11/15+7/15x){\text{e}}^{-x}]$$ (1)

where x = q²Lb/6, L is the contour length, and b is the Kuhn statistical length, which is twice the persistence length. This equation is valid for L/b > 10 and in the q-range q < 3/b. The persistence length is a measure of the rigidity of the polypeptide and is defined for polymers as the length over which the polymer naturally stays straight. A higher persistence length reveals a higher rigidity of the polymer. The persistence length therefore accounts for the rigidity of the polypeptide, and for local interactions. The contour length is the length of the fully extended chain. The contour length of a fully unfolded protein cannot exceed the product n · l₀ · f, where n is the number of residues, l₀ is the distance between two consecutive residues (l₀ = 3.8 Å), and f is a geometrical factor equal to 0.95 for a polypeptide chain. When the SAXS data for p53TAD was fit using the Krakty-Porod model, L values larger than the upper bound were observed. Since this is not physically possible, the value of L was constrained to not exceed the upper bound. It is unclear why L values larger than the upper bound were observed but the perfect linearity of the Guinier plots and the presence of repulsive interactions based on a systematic decrease in R_g as the protein concentration is increased argues strongly against aggregation. The large values of L might be due to eqn (1) that is mathematically more sensitive to the product L*b included in the adjustable parameter x = q²Lb/6, than to each parameter L and b individually, leading to a possibility of a correct L*b product with too large a value of L.

Size Exclusion Chromatography

Hydrodynamic radii for p53TAD were determined using SEC. A prepacked 16/60 Superdex 75 column (GE Healthcare, Piscataway New Jersey) with a V_o of 39.81 ml was attached to an AKTA FPLC system (GE Healthcare, Piscataway New Jersey) and equilibrated with five column volumes of 50 mM TrisHCl (pH 7.5) and 300 mM KCl. Molecular weight standards were purchased from Sigma (MW-GF-70) and included Aprotinin, Bovine Serum Albumin, Carbonic Anhydrase, and Cytochrome C. V_e was determined for each of the standards at a flow rate of 0.14 ml/min. A standard curve was generated by plotting log(MW) for the standards versus V_e/V_o. Least squares fitting of the data to a linear function gave a standard equation with a correlation coefficient of 0.997. V_e was also determined for p53TAD at 0, 2, 4, 6, and 8 M urea. Three replicate experiments were run at each concentration of urea. The elution volume, measured at the point of maximum absorbance in the elution profile, never deviated by more than ±0.4 ml at a given urea concentration, which corresponds to a change in the Stokes radius (R_h) of less than 0.4 Å. The V_e values were averaged and used to calculate an apparent molecular weight based on the standard curve and this was used to calculate the R_h based on an empirical relationship between the two quantities.⁵⁰ The elution volumes of blue dextran and acetone were measured at all urea concentrations to determine whether the permeation properties of the Superdex 75 changed in the presence of urea.⁵⁰ The elution volumes of blue dextran and acetone did not change significantly when the concentration of the urea was changed (data not shown).

Static and Dynamic Light Scattering Measurements

Both static (SLS) and dynamic (DLS) light scattering measurements were carried out using a Zetasizer Nano S (Malvern Instruments, Worcestershire, UK) with a 4 mW He-Ne laser at λ = 633 nm. The unit collects back-scattered light at an angle of θ = 173°. Sample temperature during measurements, controlled by the built-in Peltier element, was 25 ± 0.1 °C. Stock solutions of human p53TAD were sequentially filtered through 220 nm and 20 nm pore size syringe filters. The resulting samples had no large aggregates and the polydispersity obtained from DLS was less than 0.1. Actual p53TAD concentrations where obtained from uv absorption measurements at λ = 280 nm (a₂₈₀nm = 1.364 ml mg⁻¹ cm⁻¹). Scattering intensities and autocorrelation functions were determined from the average of eight to ten correlation functions, with a typical acquisition time of 180 s per correlation function. A viscosity value of η = 0.9026 mPa·s was used for the 50 mM NaH₂PO₄/50 mM NaCl buffer. This value accounts for the contributions of both salts to the water viscosity.⁵¹

Static Light Scattering Analysis

SLS measures the excess scattering due to the dissolved protein. This value is obtained by comparison against a standard of known scattering cross section (in our case, toluene), and is expressed as Rayleigh ratio R_θ.

$${\text{R}}_{\theta }=[({\text{I}}_{\text{tot}}-{\text{I}}_{\text{sol}})/{\text{I}}_{\text{tol}}]{[\text{n}/{\text{n}}_{\text{tol}}]}^2{\text{R}}_{\theta ,\text{tol}}$$ (2)

where I_tot, I_sol, and I_tol are the measured scattering intensity of the protein solution, the salt/buffer background, and of the toluene standard, respectively. R_θ,tol is the Rayleigh ratio for toluene at λ = 633 nm and the ratio n/n_tol accounts for the difference in scattering volume imaged onto the detector due to the refractive index differences between the aqueous solvent and toluene. For our set-up, the manufacturer quotes a Rayleigh ratio of R_tol = 13.52 × 10⁻⁶ cm⁻¹. The normalized Rayleigh ratio R_θ can be related to the properties of the protein in solution via

$${\text{KC}}_{\text{p}}/{\text{R}}_{\theta }=1/\text{M}+2{\text{B}}_{22}{\text{C}}_{\text{p}}$$ (3)

where KC_p/R_θ is the Debye Ratio, M is the molecular weight of the protein, C_p is the protein concentration in mg/ml, and B₂₂ is the virial coefficient, which accounts for the net effect of all intermolecular protein interactions on the thermal fluctuations. The ellipsis indicates that non-linear terms can become important at higher protein concentrations. The instrument constant K in eqn (3) is given by

$$\text{K}=(2{\pi }^2{{\text{n}}_0}^2/{\text{N}}_{\text{A}}{{\lambda }_0}^4){({\text{dn}}_0/{\text{dC}}_{\text{p}})}^2$$ (4)

where n₀ is the solvent’s refractive index, N_A is Avogadro’s number, λ₀ is the wavelength of incident light, and (dn₀/dC_p)_λ is the refractive index increment of the solvent due to p53TAD. We used the value of (dn₀/dC_p)_λ = 0.185 which is typical for many proteins.⁵² The molecular weight of p53TAD obtained from eqn (2) was 8.1 ± 0.2 kDa.

Dynamic Light Scattering Analysis

The autocorrelation function of scattered light measured in DLS yields the decay rates, G, of local concentration fluctuations for macromolecules in solution.^53–55 For data analysis, the experimentally measured (and normalized) autocorrelation function of intensity fluctuations g₂(τ) is first converted into the field autocorrelation function g₁(τ) via the Siegert relation.⁵⁴

$${\text{g}}_1(\tau )=\surd [{\text{g}}_2(\tau )-1]$$ (5)

For the essentially homogeneous distributions of monomeric protein molecules we are concerned with, the field autocorrelation function g₁(τ) will decay with a single rate

$$\mathrm{\Gamma }={\text{D}}_{\text{m}}{\text{q}}^2,$$ (6)

where D_m is the mutual diffusion coefficient and q is the magnitude of the scattering wave vector given by

$$\text{q}=(4\pi {\text{n}}_0/{\lambda }_0)sin(\theta /2)$$ (7)

Here, n₀ is the solution’s refractive index, λ₀ is the wavelength of the incident laser in air, and θ is the in-plane angle at which the scattered light is detected. Since all measurements are performed at elevated protein concentrations, both direct (e.g. electrostatic, dipole-dipole, van der Waals, hydrophobic interactions) and solvent-mediated hydrodynamic interactions among the protein molecules will alter the decay rates compared to purely thermally driven concentration fluctuations.^56–58 At moderate protein concentrations, the mutual diffusion coefficient D_m is related to the single particle diffusivity D₀ via

$${\text{D}}_{\text{m}}={\text{D}}_0[1+{\text{k}}_{\text{D}}\phi ]$$ (8)

where k_D is the sum of direct and hydrodynamic protein interactions, φ is the protein volume fraction, and D₀ is the single-particle diffusivity of the protein given by the Stokes-Einstein relation

$${\text{D}}_0={\text{k}}_{\text{B}}\text{T}/(6\pi \eta {\text{R}}_{\text{H}})$$ (9)

Here, k_B is the Boltzmann constant, T is the absolute temperature, η = η (Cs,T) is the (salt- and temperature-dependent) solution viscosity, and R_h is the hydrodynamic radius.

NMR of unfolded p53TAD

¹H-¹⁵N HSQC experiments were performed on uniformly ¹⁵N-labeled p53TAD samples in 0-6 M urea at 1 M increments. The p53TAD concentration for all samples was 0.3 mM and the buffer was 50 mM NaH₂PO₄ (pH 6.5), 50 mM NaCl, 1 mM EDTA, 0.02% NaN₃ plus the different concentrations of urea. Backbone resonances assignments for p53TAD in 0M urea were previously reported.⁴¹ Assignments of amide ¹H and ¹⁵N resonances in 1-6 M urea were determined by following the movement of the peaks at the different concentrations of urea. Amide ¹H and ¹⁵N chemical shifts were measured for each assigned residue at each urea concentration and the average chemical shift differences were calculated. These residue-specific chemical shift differences were plotted against urea concentration. The plots were best fit using the formula for a straight line and the correlation coefficients for all of the fits were greater than 0.99. The slopes for each of the residue specific fits were then plotted to show how the magnitude of the chemical shifts change as a function of urea.

Generating structural ensembles

All atom structures of p53TAD were determined using our new approach termed broad ensemble generator with re-weighting (BEGR). The BEGR method is inspired by the previous work of Ytreberg and Zuckerman and was developed to determine structural ensembles for IDPs.⁵⁹ For the current study the following three steps were utilized: (i) Generate a large pool of plausible p53TAD structures. (ii) Calculate the simulated spectrum for each structure in the pool (in this case SAXS spectra were simulated but other types of spectroscopic data can be used). (iii) Determine the probability (i.e., weights) for each structure in the pool such that the average simulated spectrum best fits the experimental spectrum.

For the first BEGR step a pool of 100,000 p53TAD structures was generated. The BEGR software uses a random build-up scheme to generate structurally diverse conformations with no bias toward structures contained in the protein data bank (PDB).⁶⁰ This is in contrast to other methods such as RANCH and ROSETTA.^27,61 The RANCH algorithm uses randomly selected amino acid conformations from a library derived from a database of coil conformations found in high-resolution X-ray structures while ROSETTA generates structures using an empirically optimized procedure to select protein fragments from the PDB. For the BEGR approach, single amino acids with optimized side-chain geometries are used as building blocks. Starting from the N-terminus, the first two amino acids of p53TAD were joined together with randomly generated Φ-Ψ angles. A test is then performed for a steric clash between the two amino acids. If a steric clash is detected then a new pair of Φ-Ψ angles is randomly generated. This process is repeated until this clash is eliminated. Using this procedure, subsequent amino acids were added until the C-terminal amino acid was reached. Generating 100,000 structures for p53TAD required less than a day of simulation on a modern desktop computer.

For the second BEGR step, the simulated SAXS spectrum for each of the 100,000 structures in the pool was generated using CRYSOL.⁶² These simulated spectra were then normalized to the experimental spectrum by multiplying the intensity values for each simulated spectrum by the mean experimental intensity averaged over the full scattering angle and then dividing this value by the average simulated intensity.

For the third BEGR step, a weight is assigned to each structure in the pool such that the weighted average simulation spectrum best fits the experimental SAXS spectrum. In order to assign these weights, the fit between the 100,000 simulated spectra and the experimental spectrum was optimized. Mathematically this corresponds to minimizing the following quantity:

$${\chi }^2=\frac{1}{k-1}\sum _{j=1}^k\left(\frac{I_j^{\mathit{sim}}-I_j^{exp}}{{\sigma }_j^{exp}}\right),\text{where}{I}_j^{\mathit{sim}}=\sum _{i=1}^N{w}_i·I_{i,j}^{\mathit{sim}},\text{and}\sum _I^N{w}_i=1.0$$ (10)

N is the number of structures in the pool (100,000 for this study), w_i is the weight of structure i, k is the number of data points from the SAXS curve (420 for this study), the experimental data points are $I_j^{exp}$ with error ${\sigma }_j^{exp}$ and the simulated SAXS data points are $I_j^{\mathit{sim}}$. To minimize χ² a Metropolis Monte Carlo simulated annealing approach was implemented.^63,64 Simulations were performed for 50 million Monte Carlo steps and the pseudo-temperature was lowered such that the temperature change decreased exponentially during the simulation. Trial moves consisted of randomly changing a single w_i value by ±0.01/N.

The numerical analysis performed for BEGR is severely underdetermined since the number of degrees of freedom is 100,000 (number of weights to be calculated) and the number of constraints is 421 (number of experimental data points plus one since the weights must sum to 1.0). However, there are several reasons that the weights obtained from BEGR are expected to be reasonable. First, solutions can be found via optimization, such as the Monte Carlo approach used here, since most of the weights are zero and the weights must be positive⁶⁵. Second, the Monte Carlo approach will not necessarily produce a unique solution but it will produce a valid solution. This is indicated by the excellent fit to the SAXS data obtained using BEGR and the consistency of these results with NMR experiments. Recent work by Stultz and collaborators confirms the notion that many different sets of weights can fit the experimental data equally well but this does not detract from the validity of the solutions determined using BEGR, especially when these solutions can be used to rationalize multiple forms of independent experimental measurements^66,67. Third, repeating BEGR using five independent pools of structures gave consistent results (data not shown).

Analyzing the structural ensembles

To test for the presence of local compactness or stiffness in the reweighted ensembles, the following analysis was performed: 1) Count the number of alpha carbons within 15 Å of a given alpha carbon for a single structure from a reweighted ensemble. This results in a value for the number of neighbors within 15 Å of each alpha carbon. These values are referred to as X1 for alpha carbon 1, X2 for alpha carbon 2, and so on. 2) Repeat step 1 for each structure in the reweighted ensemble. 3) Compute the X1–X2 correlation. This is the correlation between number of neighbors for alpha carbon 1 and number of neighbors for alpha carbon 2 in all of the structures in the reweighted ensemble. This tests whether the number of alpha carbons surrounding alpha carbons 1 and 2 change in a correlated fashion between the different structures in the reweighted ensembles. (4) Repeat step 3 for all possible pairs of alpha carbons, X1–X3, X1–X4,…, X2–X4, X2–X5,…, X(n−1)-X(n), where n is the number of residues in the polypeptide (n=73 in this study). By definition, the X2–X1 correlation is the same as the X1–X2 correlation and thus does not need to be explicitly calculated. After step 4, there are n×n values representing the correlations between the numbers of neighbors for each pair of alpha carbons in the reweighted ensemble. A high correlation value means that, within the reweighted ensemble, the numbers of neighbors for those alpha carbons tend to change together. If one of these alpha carbons has a large number of neighbors in a given structure, then the other alpha carbon is likely to also have a large number of neighbors in that same structure. If one alpha carbon has a small number of neighbors in a given structure, then the other the other alpha carbon is likely to also have a small number of neighbors. Conversely, a correlation that is zero means that, within the BEGR ensemble, the number of neighbors change independently of each other.

Results and Discussion

Radius of gyration of p53TAD

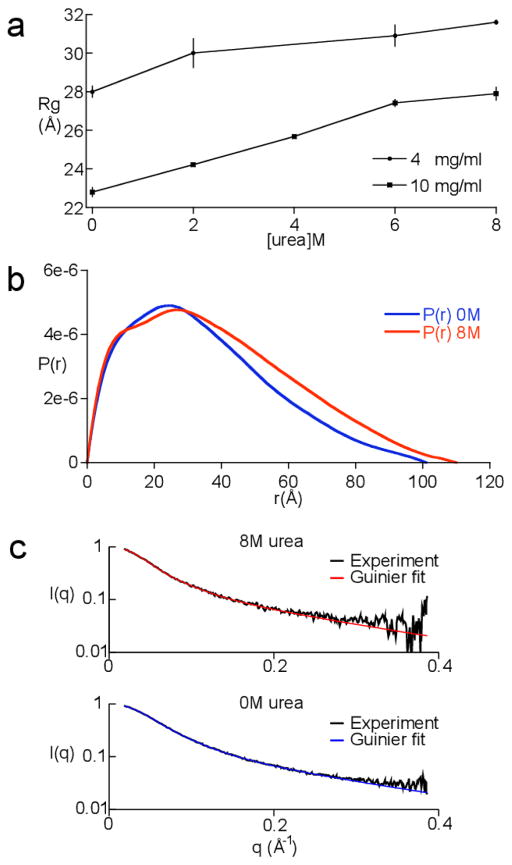
SAXS data was collected on p53TAD and processed as described in the materials and methods. The Guinier plots were perfectly linear and no trace of aggregation was detected (data not shown). Analysis of SAXS data collected over a range of concentrations (2–10 mg/ml) showed the R_g values obtained at high [p53TAD] were systematically lower than the R_g values at low [p53TAD], indicating a repulsive interaction. This is no surprise given the estimated net charge on p53TAD at pH 6.5 is 14e. Figure 1a shows a plot of R_g values for the 4 mg/ml and 10 mg/ml p53TAD scattering data collected at 0, 2, 4, 6, and 8 M urea. The scattering data collected at 4 M urea and 4 mg/ml p53TAD was discarded because the intensity of the buffer sample was so much greater than the protein plus buffer sample that it could not be reliably subtracted. This was probably due to a small bubble entrained in the capillary during data collection. The low contrast between the solvent and the solute and the resulting low signal-to-noise ratio prevented the use of data collected on 2 mg/ml p53TAD at 6 and 8 M urea. Therefore, the data collected at 4 mg/ml was used because the repulsive interactions were still weak and the signal-to-noise ratio was good.

Fig. 1.

SAXS data for p53TAD. a. R_g values for p53TAD at 0, 2, 4, 6, and 8 M urea. R_g values are shown for 4 and 10 mg/ml samples. b. Internuclear distance distributions for 4 mg/ml p53TAD samples in 0 (blue curve) and 8 M (red curve) urea. c. Fits to the scattering curves in reciprocal space. Plot shows the scattering intensity, I(q), as a function of the scattering vector, q. The data is shown in black and the fits are shown in blue and red for 0 and 8 M urea, respectively.

Figure 1b shows the distance distribution for all internuclear distances based on the Fourier transform of the entire scattering curve for a 4 mg/ml sample of p53TAD in 0 and 8 M urea. The value for the maximum diameter, D_max, extracted from this distribution is 100 Å in 0 M urea and 110 Å in 8 M urea. Figure 1c shows the corresponding fit to the scattering curve in reciprocal space, determined using GNOM, for the 4 mg/ml sample of p53TAD in 0 and 8 M urea. The scattering curves for both data sets are shown in black and the fits are shown in blue and red, for 0 and 8 M urea, respectively. This fitting procedure gave the same R _g values as the Guinier approximation. In 0 M urea a value of 28.0±0.3 Å was calculated for R_g and in 8 M urea, R_g increases to 31.6±0.1 Å. According to the power-law relationship between polymer length and the ensemble average R_g, initially proposed by Flory and experimentally validated by Doniach and Plaxco, the R_g value for a random polymer that is the same length as p53TAD should be 25.8±3.0 Å.^17,18 According to our measurements, the R_g value for native p53TAD is at the upper bound of the predicted random coil value and increases upon the addition of urea.

Krakty-Porod analysis of the SAXS data

To gain some additional insight into how the p53TAD ensemble changes in response to increasing urea concentrations, Kratky-Porod analysis was performed on the 4 mg/ml SAXS data. In 0 M urea, p53TAD has a contour length of L = 262±10 Å and a statistical length of b = 22±1 Å. In 0 M urea, the contour length and the statistical length are consistent with the values predicted for a random coil.^68,69 The values predicted for the statistical length of a random coil are between 19 and 25 Å. In 8 M urea, the contour length is L = 261±15 Å and the statistical length is b = 29±3 Å. These values are typical of the values expected for a random polymer with an excluded volume effect, which is induced by the high concentration of urea.⁷⁰

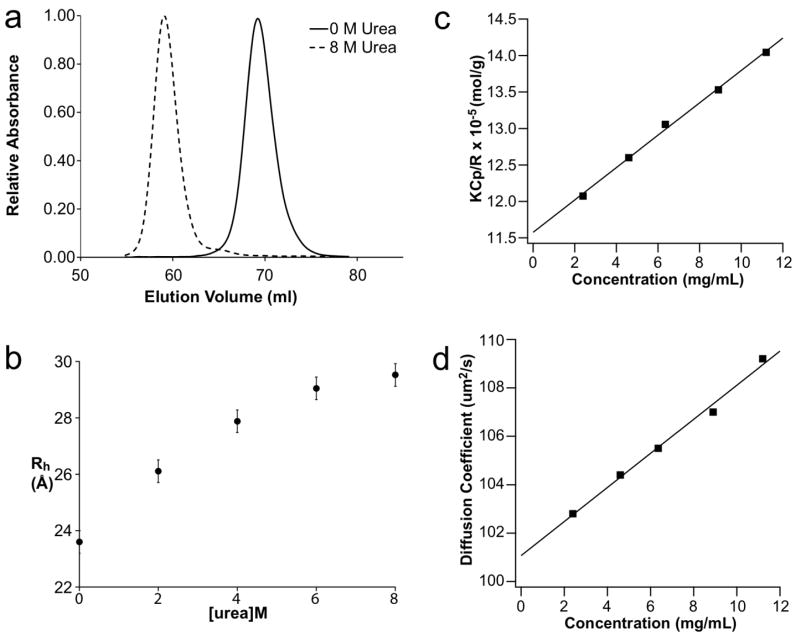
Hydrodynamic radius of p53TAD by SEC and DLS

To determine the hydrodynamic radius of p53TAD, SEC was performed in different urea concentrations. Figure 2a shows the SEC elution profiles for p53TAD in 0M and 8M urea. A hydrodynamic radius (R_h) of 23.8 Å was previously reported for p53TAD in the absence of denaturant.³² A nearly identical value of 23.6 Å was determined using the V_e measured in 0 M urea. R_h values were also determined in 2, 4, 6, and 8M urea and these values are shown in Fig. 2b. The error bars shown in Figure 2b are based on the maximum variation in V_e, which was observed during the 0 M runs. There is a clear trend toward increasing R_h values as the concentration of urea is increased with a maximum value of 29.5 Å in 8 M urea.

Fig. 2.

Hydrodynamic radii from size exclusion chromatography and static and dynamic light scattering. a. Chromatographic traces at 0 and 8 M urea. b. R_h values calculated at the different urea concentrations. c. The Debye Ratio (KCp/R) versus p53TAD concentration. d. Mutual diffusion coefficient D_m vs. p53TAD concentration. For c and d, the squares are individual measurements and the solid lines are linear fits through these data. According to eqns (2) and (4), the intercepts and slopes of these curves yield the following parameters for p53TAD: MW = 8.6 kDa, B₂₂ = 11.2 x 10⁻⁴ mL mol/g², D₀ = 101.1 ± 0.3 μm²/s, and R_h = 23.9 ± 0.1 Å.

The hydrodynamic radius of p53TAD was also measured using dynamic light scattering. Figure 2c and 2d show the results of static and dynamic light scattering measurements of p53TAD in 0 M urea, respectively. The positive slopes of either curve indicate that the prevailing direct and hydrodynamic interactions among the p53TAD monomers are repulsive, most likely due to incomplete shielding of intermolecular protein charge repulsion. The linear extrapolation of the mutual diffusivity to vanishing protein concentration results in a single-particle diffusivity of D₀ = 101.1±0.3 μm²/s. Use of the Stokes-Einstein relation yields a corresponding hydrodynamic radius for p53TAD of 23.9 ± 0.1 Å, which is in excellent agreement with the SEC results. The resolution of the diffusivity data matches previous results from the Muschol group.⁵¹

Evaluation of theoretical models for hydrodynamic radius

An empirical relationship between R_h and MW was previously developed for IDPs that behave like random coils.⁴ Using this relationship, the R_h of p53TAD is predicted to be 23.9 Å while a chemically unfolded globular protein the same size as p53TAD is predicted to have an R_h of 24.5 Å. By comparing the measured R_h values in Fig. 2 with this prediction, one would conclude that p53TAD behaves like a random coil in 0 M urea and is more extended than a random coil in 8 M urea. This conclusion is consistent with the R_g values calculated from the SAXS data collected in 0 and 8 M urea.

A recent study by Forman-Kay and colleagues suggests that proline content and net charge have a significant effect on the inherent compactness of an IDP.¹⁶ They developed an empirical relationship between polymer length and R_h for IDPs that accounts for proline content and net charge. Using this relationship, p53TAD is predicted to have an R_h of 26.6 Å. This predicted value for R_h is greater than the value measured for p53TAD in 0 M urea and smaller than the value measured in 8 M urea. The correction factors for proline content and net charge were not tested against R_g values. However, we applied the same correction factor used for R_h to the R_g value predicted using the power law relationship proposed by Flory. In this case, the predicted R_g value of 30.2 Å, is also larger than the R_g value measured in 0 M urea and is close to the R_g value measured in the presence of 8 M urea.

Comparing the predictions for R_h developed by either Uversky or Forman-Kay to the measured values indicates that the native state ensemble of p53TAD has an inherent degree of compactness that is eliminated in the chemically unfolded state. This is consistent with our previous results on the ensemble structure of p53TAD that showed a tendency for partially collapsed structures and our previous analysis of hydrophobicity and net charge, which showed that p53TAD is near the border between disordered and ordered proteins.^31,32 These comparisons also suggest that there are structures in the chemically unfolded ensemble of p53TAD that are more extended than expected for a random coil.

The empirical relationship developed by Forman-Kay and colleagues is a first attempt to use the unique sequence properties of IDPs in the prediction of R_h. However, this relationship is based on the average properties of the sequence, and does not take into account the local features. It is therefore not surprising that the study by Forman-Kay does not show any correlation between R_h and global hydrophobicity. In the next sections, we demonstrate that the degree of collapse observed for p53TAD is, in part, due to the presence of local hydrophobic clusters that are generating local residual structures. These local hydrophobic clusters are observed at the MDM2 and RPA70 binding sites of p53TAD and are involved in the coupled folding and binding of these two important protein partners.

Localized structural changes upon unfolding

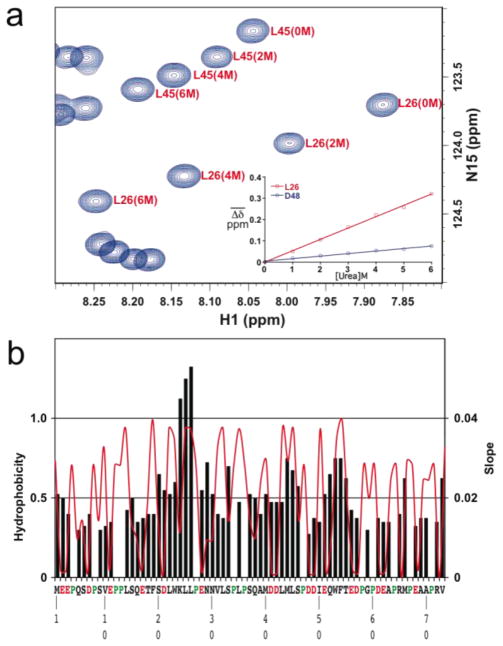
NMR resonances from ¹H-¹⁵N HSQC experiments of p53TAD in 0, 2, 4, and 6 M urea were collected and analyzed to identify the local regions of p53TAD most affected by unfolding. Amide ¹H and ¹⁵N chemical shifts for individual residues were averaged and these averaged chemical shifts were plotted as a function of urea concentration. Figure 3a shows an overlay of a selected region from the ¹H-¹⁵N HSQC spectra at 0, 2, 4, and 6 M urea. The inset of Figure 3a shows a plot for one of the most affected residues (L26) and one of the least affected residues (D48). The average chemical shift changes were fit using a formula for a straight line and the fits are shown for L26 and D48. The R² values for all the fits were >0.99 and the average slope was 0.02±0.008. The slopes for the linear fits are plotted as black bars in Figure 3b and can be used to identify the regions with the largest environmental changes. For comparison, the red line is a hydrophobicity plot for the p53TAD sequence. Some of the largest slope values correspond to nonpolar residues in the MDM2 binding site (L25 and L26) and aromatic residues in the RPA70 binding site (W54 and F55). Previous structural studies of p53TAD have shown that these two segments have some transient secondary structure and form transient long-range contacts.^32,41,44

Fig. 3.

Residue specific chemical shift changes as a function of urea. a. Overlay of a selected region from the ¹H-¹⁵N HSQC spectra at 0, 2, 4, and 6 M urea. Inset shows plots for two residues (L26 and D48). b. black bars show slope values and red line shows a hydrophobicity plot.

Structural ensembles of p53TAD

The details of our new BEGR algorithm are presented in the materials and methods. Briefly, a pool of 100,000 plausible p53TAD structures was generated using a random buildup scheme that fully samples the allowed regions of Ramachandran space and does not introduce any bias related to secondary structure preference or the structures in the PDB. These p53TAD structures are reweighted to minimize the difference between the simulated and experimental SAXS data. After performing the reweighting step, most of the structures have zero weights. In fact, less than 1% of the structures from the initial pool of 100,000 structures contribute significantly to the weighted average spectrum. For 0 M urea, 227 structures had non-zero weights, and for 8 M urea, 189 structures had non-zero weights. The term “BEGR ensemble” will be used hereafter to refer to the subset of structures with weights greater than zero.

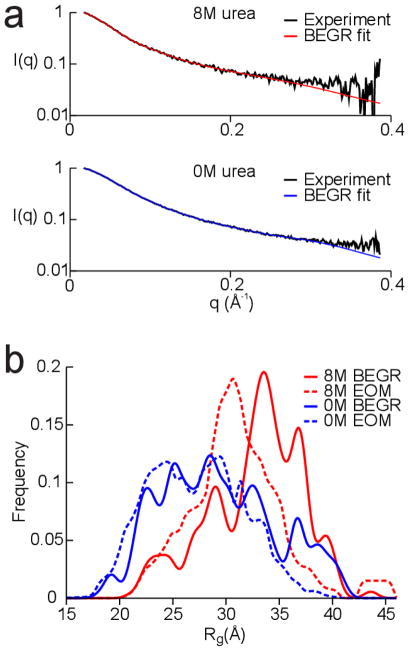
Figure 4a shows the agreement between the simulated SAXS spectra from the BEGR ensembles and the experimental SAXS spectra for p53TAD. The blue curve shows the fit to the 0 M SAXS data and the red curve shows the fit to the 8 M SAXS data. Both the 0 M and 8 M BEGR ensembles were generated using the same initial pool of 100,000 structures. These results demonstrate that broad sampling of Ramachandran space combined with reweighting is an effective way to generate an ensemble of structures that provide an excellent fit to the experimental SAXS data.

Fig. 4.

Fitting the SAXS data using the BEGR ensembles. a. Plot of the scattering intensity decay, I(q), as a function of the scattering vector, q. Black lines show the SAXS data for 0 M and 8 M urea and blue and red lines show the fits using the BEGR ensembles. b. Plot of the R_g distribution for structures from the BEGR (solid lines) and EOM (dashed lines) ensembles.

Figure 4b shows R_g distributions for the BEGR ensembles used to fit the SAXS data collected in 0 M (blue curve) and 8 M urea (red curve). The shift in the distribution of R_g values involves a reduction in the number of structures with R_g values less than 25 Å and an increase in the number of structures with R_g values greater than 30 Å. BEGR ensembles from five independently generated pools of 100,000 structures produced very similar R_g distributions for the 0 M and 8 M datasets (data not shown).

Several groups have developed protocols for generating structural ensembles of disordered and chemically denatured proteins.^{10,22,23,26–28,66,67,71–75} The ensemble optimization method (EOM) developed by Blackledge, Svergun, and colleagues was chosen for comparison with BEGR because the software is freely available and has been optimized for use with SAXS data.²⁷ Ten thousand random structures were generated using the RANCH algorithm (distributed as part of the EOM software package). This ensemble size was chosen to be consistent with the author’s suggested use of RANCH. Then, the simulated SAXS spectra were calculated for the 10,000 structures using CRYSOL. Finally, the best-fit simulated SAXS curve was generated using the GAJOE algorithm (also distributed as part of the EOM software package). The dashed lines in Fig. 4b show the R_g distributions for the EOM ensembles. The R_g distributions for the BEGR and EOM ensembles are similar with one important distinction: the 0 and 8M BEGR ensembles both contain more extended structures than the 0 and 8 M EOM ensembles. This is interesting because the R_g distributions from the initial pools of structures used by BEGR and EOM are nearly identical, which means that EOM has more extended structures available but does not select these structures. Since the EOM code is not open source it is difficult to make an in depth conclusion about the differences with the BEGR method. However, a comparison of the average R_g from the EOM and BEGR ensembles with the R_g inferred from the Guinier law does provide some indication that BEGR is doing a better job of selecting structures from the initial pool. The average R_g for the 0 M and 8 M EOM ensembles are 27.5 and 31.0 Å, respectively, and the average R_g for the 0 M and 8 M BEGR ensembles are 29.3 and 32.7 Å, respectively. The R_g inferred from the Guinier law for the 0 M SAXS data is 28.0 Å and for the 8 M SAXS data is 31.6 Å. It has been demonstrated that the Guinier law will underestimate the true R _g if there are highly extended structures present in the ensemble⁷⁶. It is clear from the internuclear distance distributions shown in Figure 1b that there are highly extended structures present in the p53TAD ensemble and thus that the true R_g should be slightly larger than the value inferred from the Guinier law. Exactly how much larger the R_g value should be is not clear, but the fact the BEGR is giving a larger value than EOM suggest that it is doing a better job of selecting structures from the initial pool. It is also possible that BEGR has better structures to choose from since it generates all atom models and EOM is a coarse grain approach.

Identifying regions of local compactness or stiffness in the high weight structures

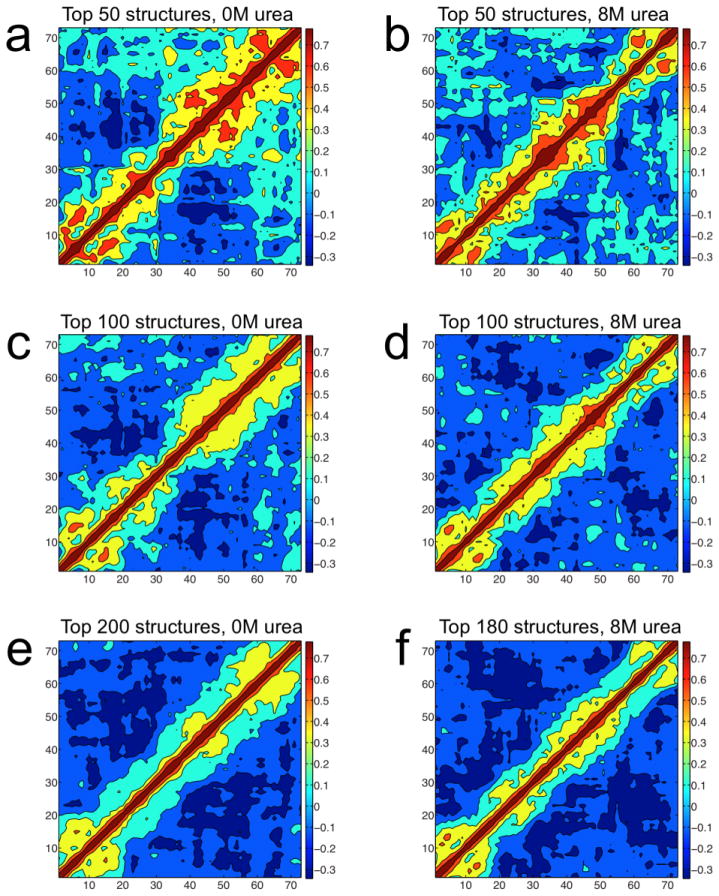
SAXS provides information about the distribution of conformations in the equilibrium ensemble at a resolution of about 15 Å. Higher resolution information is provided by complementary methods, such as NMR or molecular modeling. Using BEGR, in combination with NMR results presented above, possible regions of local compactness or stiffness along the polypeptide chain were identified. To determine whether the high weight structures in the 0 M and 8 M BEGR ensembles contain regions that are locally compact or stiff they were analyzed for correlations as described in the materials and methods. The correlation plots based on this analysis are shown in Figure 5. Positive correlations in these plots are expected for regions of the chain that experience similar positional variation between the individual structures in the BEGR ensembles. Positive correlations for sequential residues are an indication that this region of the chain is locally compact or stiff. The 50 top weighted structures from the 0 M BEGR ensemble have strong positive correlations at the two termini, the MDM2 binding site (S17-N29), and the RPA70 binding site (M40-D60). These correlations are weaker but remain positive for the 100 and 200 top weighted structures. The positive correlations observed at the MDM2 and RPA70 binding sites are probably an indication of local compactness that is induced by the presence of transient secondary structure. This is consistent with the NMR data presented in Figure 3, which shows that the largest structural changes upon urea unfolding are localized to these binding sites, suggesting the transient secondary structure present in these binding sites is destabilized by urea. The positive correlations observed at the two termini are probably an indication of local stiffness that is induced by the presence of several prolines. The top weighted structures from the 8 M BEGR ensemble also show positive correlations, but the pattern is different when compared to the 0 M BEGR ensemble. In particular, the distribution of positive correlations for the 8 M BEGR ensemble is more localized to the backbone and more uniformly distributed along the chain. This indicates stiffening along the entire chain, which is consistent with the Krakty-Porod analysis of the 8 M SAXS data and is expected for a linear polymer with an excluded volume effect. Positive correlations observed at the two termini of the 8 M BEGR ensemble are similar to the 0 M ensemble and are relatively unaffected by the addition of urea. If the local stiffening at the two termini is being induced by the prolines, then this behavior does not appear to be very sensitive to the presence of urea.

Fig. 5.

Correlation plots for number of neighbors using the top weighted structures from the 0 and 8 M BEGR ensembles. The observed correlations vary from −0.3 (dark blue) to 0.7 (dark red) and a scale bar is shown to the right of each plot. Amino acid position is shown on both axes. Correlation plots for a) 50, c) 100, and e) 200 top weighted structures from a total of 227 structures in the 0 M BEGR ensemble, representing representing 50.0%, 78.5%, and 99.5% of the total weight, respectively. Correlation plots for the b) 50, d) 100, and f) 180 top weighted structures from a total of 189 structures in the 8 M BEGR ensemble, representing 55.4%, 83.2%, and 99.8% of the total weight, respectively.

Similar patterns of positive correlations were observed for five independently generated BEGR ensembles used to fit the 0 M and 8 M SAXS data (data not shown). While it is not reasonable to make any claim of accuracy based on this result it does appear that the BEGR method can generate realistic and reproducible ensembles for IDPs. No consistent positive correlations were observed when the same analysis was performed on 50, 100, and 200 randomly selected structures from the initial pool of 100,000 structures.

Conclusions

This study presents the most detailed investigation to date characterizing the chemical unfolding of an IDP. While it is well established that urea is capable of inducing the unfolding and expansion of ordered proteins, the ability of this destabilizing osmolyte to affect the dynamic structures of IDPs has not been thoroughly examined. The hydrodynamic properties of the native and chemically unfolded forms of p53TAD were investigated using SAXS, SEC, DLS, and NMR. The native state of p53TAD has hydrodynamic dimensions consistent with the values expected for a random coil, and the chemically unfolded state of p53TAD has hydrodynamic dimensions that are significantly greater than the values expected for a random coil. Auton and Bolen recently showed that newly exposed side chains are responsible for 75% of the increase in surface area when ordered proteins are unfolded with urea, but the energetics of unfolding is dominated by interactions between the denaturant and the backbone.⁷⁷ If this relationship can be applied to IDPs, then the observed increase in the hydrodynamic dimensions of p53TAD is due to the exposure of new side chains. For this to happen, the side chains had to be buried in the first place. We recently showed that two segments of p53TAD, corresponding to the MDM2 and RPA70 binding sites, make transient long-range contacts.³¹ These transient contacts were not observed in a structural ensemble based on residual dipolar coupling data.⁴⁵ These two segments contain four aromatic amino acids as well as other nonpolar amino acids. Exposure of all or part of the side-chains for these residues could be responsible for the observed increase in the hydrodynamic dimensions of chemically unfolded p53TAD. The data presented in Fig. 3 provides strong support for this mechanistic interpretation.

This study also demonstrates that a large pool of simulated structures with broad conformational properties can be used to determine a structural ensemble for an IDP. There is no feature of the BEGR approach that is specific to the p53TAD system and it should therefore be applicable to other IDPs. The BEGR algorithm provided structures with larger R_g values than observed using other methods and we think this is an important feature for generating more realistic structural ensembles of IDPs. We also demonstrated that SAXS data could be used to identify possible regions of local compactness or stiffness in an ensemble model of a disordered protein. The analysis developed to identify these features is unique and is not related to the standard measures for comparing structures. For instance, clustering structures by backbone RMSD or Φ-Ψ dihedral angles did not identify regions of local compactness or stiffness (data not shown). The identification of locally compact or stiff regions in the BEGR ensemble demonstrates that the shape envelope of an IDP can be deconvoluted to identify local structural features. A recent report also demonstrates that this level of molecular detail can be extracted from SAXS data⁷⁸.