An Ideal Observer Analysis of Visual Working Memory

Abstract

Limits in visual working memory (VWM) strongly constrain human performance across many tasks. However, the nature of these limits is not well understood. In this paper we develop an ideal observer analysis of human visual working memory, by deriving the expected behavior of an optimally performing, but limited-capacity memory system. This analysis is framed around rate–distortion theory, a branch of information theory that provides optimal bounds on the accuracy of information transmission subject to a fixed information capacity. The result of the ideal observer analysis is a theoretical framework that provides a task-independent and quantitative definition of visual memory capacity and yields novel predictions regarding human performance. These predictions are subsequently evaluated and confirmed in two empirical studies. Further, the framework is general enough to allow the specification and testing of alternative models of visual memory (for example, how capacity is distributed across multiple items). We demonstrate that a simple model developed on the basis of the ideal observer analysis—one which allows variability in the number of stored memory representations, but does not assume the presence of a fixed item limit—provides an excellent account of the empirical data, and further offers a principled re-interpretation of existing models of visual working memory.

Introduction

Visual working memory (VWM)—defined as the ability to store task-relevant visual information in a rapidly accessible and easily manipulated form (Luck, 2008)—is a central component of nearly all human activities. It plays a critical role in online movement control (Brouwer & Knill, 2007, 2009), integration of visual information across eye movements (Irwin, 1991), visual search (Desimone & Duncan, 1995; Oh & Kim, 2004), and gaze correction following saccadic error (Hollingworth, Richard, & Luck, 2008) among other functions. Given its biological importance, it is perhaps surprising that the capacity of this system is severely limited. Many investigations of human performance have revealed that we can only accurately store a surprisingly limited amount of visual information in working memory (for reviews, see Luck, 2008; Brady, Konkle, & Alvarez, 2011).

In recent years there have been numerous attempts to define and quantify what is meant by VWM capacity. Until recently, the prevailing view has held that memory capacity is defined by a small, fixed number of discrete “slots” (Cowan, 2001; Awh, Barton, & Vogel, 2007; Lee & Chun, 2001; Luck & Vogel, 1997; Olsson & Poom, 2005; Vogel, Woodman, & Luck, 2001; Rouder et al., 2008; Morey, 2011), each of which can store a single visual object. The origins of this item-limited conception of working memory capacity may be attributed to Sperling (1960) who found that when experimental participants were asked to recall letters or digits briefly presented in arrays, the participants were able to report only four to five items correctly, even though it could be ascertained that nearly all items were present in iconic memory. Around the same time, George Miller (1956) proposed that humans possess a limited “span of immediate memory” of around seven items, drawing on experimental evidence from a variety of sources.

According to the simplest form of the item-limit model of visual working memory, visual objects can be maintained in memory with accuracy that is independent of the total number of items stored. That is to say, storing additional items does not degrade the quality of each memory representation. Further, this basic model does not posit any constraints on the visual complexity of an individual object stored in memory. For example, Vogel et al. (2001) found that the estimated capacity limit of 3–4 items did not decrease when subjects were required to simultaneously store the color and orientation of objects, compared to the simpler task of storing only a single visual feature dimension.

Although successful in accounting for many aspects of empirical behavior, this basic slot model has been challenged. Several studies have shown that the complexity of visual objects interacts with memory capacity (Alvarez & Cavanagh, 2004; Luria, Sessa, Gotler, Jolicoeur, & Dell’Acqua, 2010), or that memory performance is higher when objects are taken from a domain of visual expertise (Curby, Glazek, & Gauthier, 2009). However, some studies have found no effects of familiarity on visual change detection performance (e.g., Pashler, 1988), and subsequent research has suggested that it may be the precision, and not number of representations, that are impacted by object complexity or familiarity (Awh et al., 2007; Scolari, Vogel, & Awh, 2008). Other researchers have explored how the precision of features stored in visual working memory may vary as a function of the number of items that are concurrently stored (Palmer, 1990; Wilken & Ma, 2004; Bays & Husain, 2008; Bays, Catalao, & Husain, 2009; Bays, Wu, & Husain, 2011). Based on the finding that memory precision appears to decrease even when as few as 2 items are stored, it has been proposed (Palmer, 1990; Wilken & Ma, 2004; Bays & Husain, 2008) that VWM capacity does not consist of a set of independent representations (slots), but is rather defined by a single, continuous pool of resources that is divided among all visual objects in a scene: When two objects are stored, each receives half of the available resources. As a result, the precision of memory representations is not constant, but depends on the total number of items stored. Countering this hypothesis, a more recent version of the item-limit model, known as the ‘slots+averaging’ model (Zhang & Luck, 2008; Cowan & Rouder, 2009; D. E. Anderson, Vogel, & Awh, 2011) holds to the claim that there are a fixed number of slots (hypothesized to be around 3–4), but when fewer than the limit are stored, two slots may ‘double up’ by storing the same object, resulting in an increase in memory precision for that object.

While both item-limit and continuous resource models are able to account for a range of empirical findings, neither has been defined in enough detail to provide complete theories of human VWM or to support quantitative predictions of human performance across a broad range of tasks and conditions. An important limitation of both models is that the relationship between hypothesized capacity limits and absolute performance has not been fully specified. In the case of item limit models, an open question concerns how the precision of representations should be constrained for items stored in individual slots. Existing item limit models specify one type of capacity limit, on the maximum number of items that can be stored, but offer little or no theoretical contribution regarding the capacity limits for individual items represented in individual slots. The continuous resource model assumes that performance is constrained not by a a discrete item limit, but rather by a central pool of resources (for example, encoding information via populations of neurons). However, in existing versions of the model there is no task-independent way of quantifying the overall capacity of visual memory, and consequently the model cannot predict in absolute fashion how memory capacity should relate to behavioral performance.

In the present paper, we address these shortcomings by developing a theoretical framework for studying and understanding how limits on memory capacity relate to observed limits on performance. Rather than proposing theoretical mechanisms a posteriori to the empirical phenomena of visual memory, we instead develop predictions for behavior using the formal framework of information theory (Shannon & Weaver, 1949). In adopting this approach, the present analysis falls under the family of ideal observer analyses (Geisler, 2003, 2011) that have been successfully applied to understanding other aspects of the visual system (Pelli, 1990; Knill & Richards, 1996; Najemnik & Geisler, 2005; Sims, Jacobs, & Knill, 2011).

In specifying the optimal performance for a given task, an ideal observer analysis serves as an important benchmark for comparison with human behavior. If humans are found to behave in close approximation to the ideal observer, then their behavior can be explained as a rational consequence of the information available in an environment and known processing constraints on performance. Furthermore, any performance limitations predicted by the analysis can be given a strong theoretical, rather than speculative, interpretation. Finally, the framework follows in the spirit of sequential ideal observer analysis (Geisler, 1989), in which information coding constraints imposed at different stages of processing in the human visual system are folded into the definition of an ideal observer, allowing one to infer the relative impact of different components of visual processing on performance. The framework supports modeling the constraints imposed by different functional architectures for VWM (e.g. continuous resource vs. slots) on information encoding and hence on psychophysical performance in a variety of tasks. This supports “strong inference” comparisons of qualitatively different models of VWM from empirical data (Platt, 1964).

The starting point of the analysis is the fact that visual working memory may productively be studied as an information transmission channel. Unlike artificial communication systems, the purpose of human memory is not, primarily, to transmit information across large distances, but rather to efficiently store and transmit information across time. In framing our analysis of VWM around this basic point, the resulting construct of a capacity limit is quantitative, theoretically grounded, and completely task independent. Specifically, memory capacity is formally defined in terms of Shannon information, or equivalently, the more familiar unit of bits. Much of the present analysis draws on results from a branch of information theory known as rate–distortion theory (Shannon & Weaver, 1949; Berger, 1971). Rate–distortion theory provides the theoretical bounds on performance for any capacity-limited communication system. That is to say, for a given capacity limit, no physical system (biological or artificial) can exhibit performance that exceeds the limits defined by the theory. As applied to visual working memory, rate–distortion theory predicts the optimal performance of human memory, when performance is constrained by a fixed information capacity.

Rather than defining a single, specific model of visual memory, the ideal observer analysis instead serves as the basis for a novel theoretical framework that can be used for developing and evaluating different models of VWM. The common element among models developed using this framework is the quantitative relationship between a fixed memory capacity, specified using information-theoretic constructs, and the absolute levels of human performance that can be achieved under the given capacity limit. Different models may entertain different assumptions regarding the encoding process¹ for visual memory (for example, whether a fixed number of items are stored, as hypothesized by discrete item limit models), and how capacity is divided among items stored in memory. Interestingly, both discrete slot and continuous resource models can naturally be placed within the resulting theoretical framework. As a result, existing models are given a stronger theoretical interpretation, and as we demonstrate, can be systematically compared and evaluated by adding or removing assumptions and constraints.

Beyond providing a principled re-interpretation of existing models, the ideal observer analysis also yields quantitative predictions for human performance, including a novel prediction regarding the relationship between memory precision and the variance of visual features in the environment. In particular, the ideal observer analysis predicts that when performance is constrained by a capacity bottleneck, visual features with low variance in the environment are fundamentally easier to encode (resulting in higher memory precision) than features with high variance. In the present paper two behavioral experiments are described that are designed to test, and ultimately confirm this prediction.

It is then demonstrated that a simple model derived from the ideal observer analysis is able to offer a quantitative and parsimonious account for the data. We find that human performance across both of our experiments is best characterized not by existing discrete slot or continuous resource models. Rather, the results suggest that encoding variability plays a large role in accounting for VWM performance. According to this view, items are probabilistically selected to be encoded in visual working memory, such that there is trial-to-trial variability in the number of stored items. Unlike the continuous resource model, people may sometimes encode only a small subset of stimulus items in a given display. Previous discussions of item limit theories have allowed for the possibility of trial-to-trial variability in the number of stored representations (e.g., Vogel et al., 2001; Luck, 2008, p. 56), but the relative contribution of this variability has not been explicitly tested in item-limit models fit to human data. Our results support the hypothesis that memory variability alone, in the absence of an explicit item limit, can account for much of the empirical properties of VWM performance (for a related model, see Van den Berg, Shin, Chou, George, & Ma, 2012). According to the best interpretation of the present data, people may sometimes encode and remember many items with low precision, and sometimes remember a few items precisely.

In the next section we provide a brief background on rate–distortion theory. We then apply the theory to develop the ideal observer analysis of visual working memory, before describing two experiments that test the predictions of the analysis.

Background on Rate–Distortion theory

Claude Shannon noted in his seminal work on information theory that “the fundamental problem of communication is that of reproducing at one point either exactly or approximately a message selected at another point.” (Shannon & Weaver, 1949, p. 31). By stating the basis of information theory in this completely general form, Shannon recognized that the results from the theory are applicable to any domain where information must be conveyed over time or space. Human visual working memory, according to this understanding, is a communication channel that functions by attempting to accurately transmit visual information from the time that it is first received by the sensory apparatus, to the moment that it is later recalled or further processed to aid in performing a task. This section first considers the properties of a completely abstract, but optimally performing communication channel. In the next section, it is shown how the properties derived for this abstract channel have direct implications for the performance of human visual working memory.

Intuitively, we develop a model of VWM according to which memory representations are noise-corrupted versions of incoming sensory signals. The amount of capacity available to memory determines the amount of noise that corrupts each representation: If capacity is high, memory representations are accurate, and largely uncorrupted by noise. If memory capacity is low, then each memory representation consists of a highly noise-corrupted version of the original sensory signal, and the accuracy of memory is expected to be poor. The visual working memory system is assumed to implement an optimal (Bayesian) decoder for these noisy representations. That is to say, given a particular noisy encoding of a sensory signal, the memory decoding process attempts to accurately reconstruct the original visual feature. This model further assumes that memory representations are adapted to the statistics of features in the environment: the optimal memory reconstruction is defined by a weighted combination of the noisy information available from memory, and the prior probability of different feature values determined by past experience or context.

The present analysis deals with the case where visual working memory must store simple visual features such as line length or orientation. These features are continuous-valued, and in a particular task or environmental context can be described by a probability density function. For example, if x is the length of a line segment, then the context of previous trials or past experience might establish that x is a sample from some distribution p(x) (such as a Gaussian distribution with a particular mean and variance). The task for visual working memory is to store an accurate representation of x over the relevant retention interval. Acknowledging the fact that memory is imperfect, the remembered feature value will in general be different from the sensory input. If x is defined as the input to memory, and x_out as the remembered feature value, then it is meaningful to treat visual working memory as a communication channel with a conditional channel distribution p(x_out | x). The channel distribution specifies the probability distribution over possible memory representations for a given visual feature.

An important quantity that characterizes this channel is its average information rate. Intuitively, if the channel is very noisy or otherwise limited, then observing x_out will, on average, leave substantial uncertainty regarding the original feature value x; such a channel would be intuited to have a low information rate. Conversely, a noise-free information channel will be such that it is possible to accurately estimate x by observing only the channel output. More formally, the information rate, R, for a particular channel and information source is defined as the average mutual information of the channel input and output,

$$\begin{array}{l}R=I(x,x_{\text{out}})\\ =\iint p(x_{\text{out}}\mid x)p(x)log\left[\frac{p(x_{\text{out}}\mid x)}{p(x_{\text{out}})}\right]\text{d}x{\text{d}x}_{\text{out}}.\end{array}$$ (1)

Mutual information is a mathematical quantity that specifies how much the observation of one variable reduces the uncertainty regarding the value of another variable. This equation therefore captures the intuition that a channel with a high information rate will, on average, reduce much of the uncertainty regarding the input value x after observing the channel output x_out. When the logarithm is taken base 2, the information rate for a channel is measured in units of bits. A channel with an information rate of R bits allows for perfectly discriminating between 2^R different values (assuming all values are equally likely to occur); thus, accurately reporting the outcome of rolling an 8-sided die would require a channel with an information rate of at least 3 bits. The use of the term rate is due to the fact that information rate measures the average amount of information transmitted per event, averaging across a long sequence of random events (for example, repeatedly rolling a die). As applied to human VWM, the information rate of memory, as measured in bits, is the average quantity of information preserved about visual features over a given retention interval.

One complication that arises for the case of continuous-valued features such as line length or orientation is that channels with finite information rate can transmit only an approximation to values drawn from continuous distributions. Information theory dictates that in this case, it is guaranteed that on average, some amount of information will be lost in the process of storing features in visual working memory. Given this fundamental limitation, an important question arises in designing or understanding any physical communication system. For a channel with a finite information rate R, what is the smallest possible error that can be achieved by the given channel? Or alternatively, for a desired level of performance, what is the minimum information rate necessary for a channel to achieve this criterion performance?

The branch of information theory that addresses these questions is known as rate–distortion theory (Shannon & Weaver, 1949; Berger, 1971). Fundamentally, rate–distortion theory provides the optimal solution to the problem of information storage or transmission, when performance is constrained by the capacity limit of a channel. The two central constructs in the theory are the average information rate of a channel, defined for continuous-valued information sources in Equation (1) and the channel distortion, D. The distortion of a channel is defined by a function d(x, x_out) that assigns a numerical cost to the event that an input value x is reproduced by the communication channel as x_out ≠ = x. Intuitively, a perfect communication channel would introduce zero discrepancy between the channel input and output, and would have zero distortion. The function d(x, x_out) therefore defines the criterion for performance of the channel. The choice of a specific distortion function can vary according to the application. However, a common distortion function is the squared error difference between the channel input and output, d(x, x_out) = (x_out − x)². This choice of distortion function leads to a channel distortion D given by averaging over the joint distribution of x and x_out:

$$\begin{array}{l}D=\text{E}[d(x,x_{\text{out}})]\\ =\iint {(x_{\text{out}}-x)}^{2}p(x_{\text{out}}\mid x)p(x){\text{d}x}_{\text{out}}\text{d}x.\end{array}$$ (2)

With an information rate (1), and distortion function (2) in place, it is possible to characterize an optimal communication channel in the following manner. For a fixed information rate R, one would like to select, out of the space of all possible communication channels with the specified rate, the one that achieves the smallest possible distortion D. Alternatively, one may fix a criterion level of performance, and select the channel that achieves this performance using the fewest bits, on average, to encode or transmit information. Formally, the relationship between these two quantities is characterized by an equation known as a rate–distortion function (Berger, 1971). This function provides the theoretical bounds on performance for a fixed information capacity (the smallest possible D for a given R), and equivalently, a theoretical minimum capacity R necessary to achieve a fixed level of performance D. In particular, in this paper we will consider the case where the information source consists of independent random variables drawn from a stationary Gaussian distribution, and the distortion function to be minimized is assumed to be the squared-error. In this case, it can be shown (Berger, 1971) that the optimal rate–distortion function is given by

$$R(D)=\frac{1}{2}max\left(0,log\frac{{\sigma }^2}{D}\right)$$ (3)

where σ² refers to the variance of the Gaussian distribution.

This function is plotted in Figure 1 for a Gaussian information source with arbitrary mean and unit variance. The information rate is infinite at zero distortion, implying that perfectly transmitting values from a continuous distribution would require an infinite number of bits². It should be emphasized that the rate–distortion curve represents a theoretical bound on the performance of any communication channel. No physical system can exist that achieves a performance level D using fewer than R(D) bits, on average, to encode or transmit information. This infeasible region is indicated by the shaded area in Figure 1. As a direct consequence of this fact, the rate–distortion curve can also be used as a direct measure of the minimum capacity of any communication channel. By measuring the distortion of an information transmission system, one can directly compute the minimum information rate necessary to achieve this level of performance. If the channel can be shown to transmit information at an average rate of R bits, then it is also the case that the capacity of the channel must be ≥ R bits.

Figure 1.

Rate–distortion curve for a Gaussian information source and squared error distortion criterion. The curve indicates the theoretical minimum information rate necessary to achieve a specified level of distortion. The shaded region indicates the infeasible region: No physical system can exist that achieves a performance level D using fewer than R(D) bits, on average, to encode information.

All of the properties and results in this section have been derived for an abstract communication channel, without regard for the physical implementation of that channel. However, the results obtained hold equally true if the physical channel consists of a fiber optic cable, a pulsed laser, or a population of biological neurons. Consequently, these results are equally applicable to quantifying the performance of human visual working memory. The next section explores the specific implications of the rate–distortion framework for studying and understanding human visual working memory.

An Ideal Observer Analysis of Human Visual Working Memory

In this section we develop an ideal observer analysis (Geisler, 2003, 2011) of human visual working memory, building upon the theoretical results presented in the previous section. Ideal observer analysis is an approach to studying perceptual systems that proceeds by determining the theoretical upper bounds on performance, given uncertainty inherent in the environment, as well as internal factors that limit information processing. In the present case, two internal factors contribute to limiting human performance. First, external information sources are corrupted by sensory noise before entering memory. Second, it is assumed that memory itself has a finite capacity, but that memory performs optimally subject to this capacity constraint.

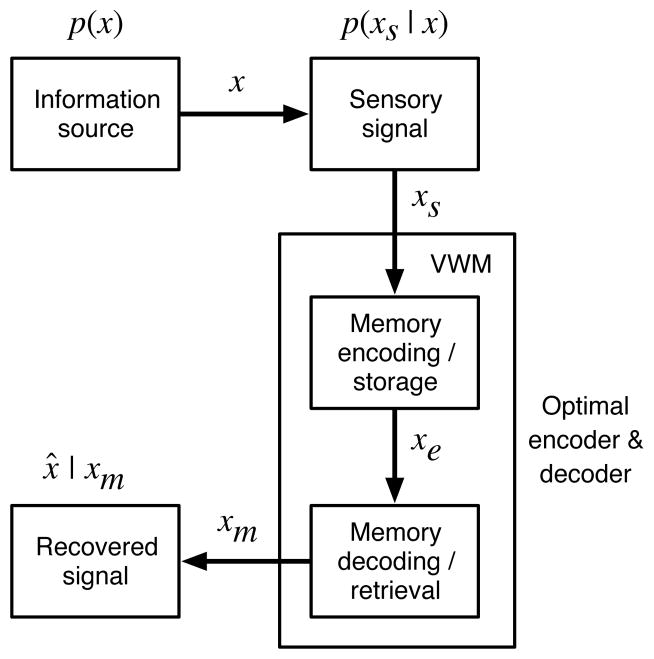
A schematic illustration of the basic memory system is given in Figure 2. As a running example, consider the task of comparing the size of two apples that are sequentially examined. This task involves looking at and remembering the size of the first apple, and then looking at a second apple and comparing its visual size to the remembered size of the first apple. Following the notation of Figure 2, we define the size of the first apple as x. All apples fall into a typical range of sizes, which can be described by the probability distribution p(x). For this example, we assume that the size of apples can be described by a Gaussian distribution with mean μ_w and variance ${\sigma }_w^2$. Before we can store the size of a particular apple in visual memory, it must first be encoded by the sensory system. It is known that the sensory encoding process is both noisy and imperfect, resulting in a transformed signal x_s, which can be described by the conditional distribution $p(x_s\mid x)=\text{Normal}(x,{\sigma }_s^2)$, where ${\sigma }_s^2$ defines the variance of the sensory noise. This noisy sensory signal defines the input to VWM.

Figure 2.

A schematic diagram of the ideal observer model of visual working memory. The information source is defined by a probability distribution, p(x), samples of which correspond to visual features to be stored in VWM. Before entering memory, the signal is encoded via the sensory system, resulting in the (noisy) sensory signal x_s. This signal is stored, and then retrieved from VWM in an optimal manner, subject to a capacity limit. The output of memory, x_m, represents the optimal estimate of the incoming sensory signal subject to the capacity constraint. A final decoder is then used to infer the optimal estimate of x, labeled as x̂.

Our model assumes that the operation of visual working memory is defined by two processes: encoding (or storing) visual features in memory, and the subsequent retrieval (or decoding) of the stored memory representations. The box labeled VWM in Figure 2 corresponds to this encoding and decoding process. How should the memory channel be designed in order to perform optimally? Based on the results from rate–distortion theory presented in the previous section, it is known that for a given information rate, there is a minimum achievable distortion. The ideal observer analysis is therefore designed such that it achieves this theoretical bound. Specifically, the memory encoding is defined as x_e, with a conditional distribution $p(x_e\mid x_s)=\text{Normal}(x_s,{\sigma }_e^2)$. The magnitude of encoding noise is chosen such that the memory channel achieves a specified information rate R (given in bits):

$${\sigma }_e^2=\frac{{\sigma }_w^2+{\sigma }_s^2}{2^{2R}-1}.$$ (4)

The supplemental material provides a full derivation for this equation. Intuitively, when memory capacity is high (corresponding to a large value of R), the magnitude of encoding noise will be small, such that the memory encoding accurately reflects the sensory representation of the apple’s size; when memory capacity is low, the memory encoding x_e will an unreliable indicator of x_s.

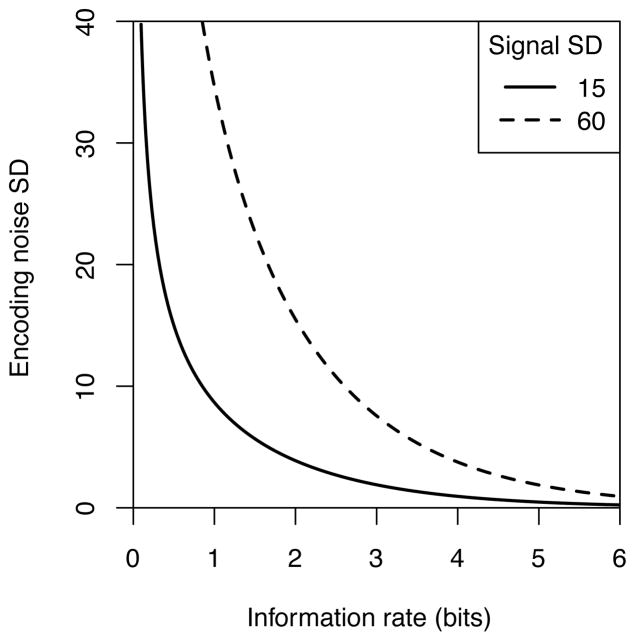
As seen from Equation (4), for an optimal memory channel the amount of corrupting noise depends not only on the information rate, but also on the variance of features in the environment ( ${\sigma }_w^2$), such that visual features with higher variance lead to noisier memory representations. Intuitively, one can think of this effect as the result of having to distribute a fixed capacity over a wider range of possible feature values. Figure 3 plots the standard deviation of encoding noise as a function of the information rate of memory, for visual features with a low (solid line) or high (dashed line) variance. For a fixed capacity, the amount of encoding noise is predicted to increase with the variance of visual features in the environment.

Figure 3.

Standard deviation of corrupting noise added to sensory signals that are stored in VWM, as a function of the information rate of memory (measured in bits) and variance of the features in the environment. This figure assumes a constant level of sensory noise, set to SD = 5, close to the value obtained in fitting the model to empirical data from the orientation experiment (Table A1).

The decoding process is implemented as a Bayesian decoding process that infers the most probable (maximum a posteriori) estimate of the original sensory signal, labeled as x_m in Figure 2. As shown in the supplemental material, the combination of a Gaussian noise encoding and Bayesian decoder achieves the theoretical rate–distortion bound, such that no alternative system could achieve a lower distortion for a given information rate. In our example, this means that memory minimizes the average squared error between the sensory size of an apple, and its remembered size, subject to a constraint on the information rate. A squared-error cost function has previously been found to approximate the biological cost function on motor error (Körding & Wolpert, 2004), and therefore is a reasonable first choice for characterizing the biological cost on memory error. Note that the assumption that memory attempts to minimize squared error is subsequent to the fact that a given amount of capacity (R) has been allocated to encoding that particular item; the question of how capacity is divided between multiple items in a visual scene is a separate issue, which we return to later.

So far, it was shown that the output of VWM represents the most accurate reconstruction of its sensory input, subject to a finite information rate limit. For an individual performing a particular task, the true feature value, x, may be of more importance than its noisy sensory encoding x_s. If the individual possesses knowledge of the statistics of the information source and the noise characteristics of its sensory system, it is straightforward to extend the model to compute a minimum mean-square error (MMSE) estimate of x given the memory signal x_m. In particular, the MMSE estimate x̂ is given by

$$\widehat{x}=\frac{{\mu }_w{\sigma }_s^2+x_m{\sigma }_w^2}{{\sigma }_w^2+{\sigma }_s^2}.$$ (5)

This equation can also be interpreted in terms of an optimal Bayesian inference: the best estimate of the visual feature is given by a weighted combination of the prior distribution (with mean μ_w) and the information available from memory (x_m).

Returning to our running example, the value x̂ represents the best possible estimate of the size of a particular apple, where the size was stored in a limited-capacity visual working memory system. To compare the size of two apples, the individual can simply compare this optimal memory estimate to the (noisy) sensory signal corresponding to the size of the comparison apple.

As we have shown, the ideal observer analysis generates the direct prediction that as the variance of features in the environment increases, the precision of memory should decrease. However, so far the analysis has been limited to the case where only a single item must be stored in visual working memory. This leaves open the question of how memory stores multiple visual features simultaneously. For example, consider the task of remembering the sizes of six apples. In this case, is a single memory capacity divided among each apple, such that each is encoded with R/6 bits? Or are there independent memory capacities for each item stored? Is it even preferable to encode all six apples, perhaps with decreased precision, or should we instead focus our limited resources on a small subset of items?

There is no universally optimal solution to this tradeoff, and it is possible to construct tasks with different performance demands where different allocation strategies are optimal. Our approach is therefore to examine a family of related models, all linked by the common framework of rate–distortion theory, but differing in their assumptions of how memory capacity is divided and distributed among multiple items. One of the models considered is optimal for the particular experiments reported in this paper, but this same model may be suboptimal in tasks more closely matching the demands of the natural environment. However, each model is optimally efficient in the sense of minimizing the squared-error in memory representations, subject to the constraints of a fixed information rate and a particular encoding strategy.

In the next section, we report an experimental test of the predictions derived from different models developed on the basis of the ideal observer analysis. To preview our results, we find that performance is best explained not by a fixed item limit, nor by the assumption that subjects encode all stimulus items. Instead, the results favor a model according to which there is trial-to-trial variability in the number of items stored in visual working memory, without imposing an upper limit on the number of stored items.

Experiments

In this section we describe two experiments conducted to evaluate the predictions of the ideal observer analysis of visual working memory. The two experiments differed in terms of the visual feature that participants had to store in VWM. In one experiment, participants were tested on their memory for the angular orientation of arrows, while in the other experiment, participants were tested on their memory for the length of line segments. In both experiments, we manipulate the set size (number of items in the display) as well as the variance of the distribution over features. Based on the theoretical results derived in the previous section, we predict that in conditions with high variance over features memory performance should degrade. However, the ideal observer analysis does not uniquely predict how performance should drop, for example, whether subjects will encode fewer items with higher precision, or a constant number of items but with lower precision. Thus, a further purpose of the experiments is to empirically address this question. Since the two experiments used a similar procedure, the experiments are described together.

Method

Participants

Twenty eight volunteers from the University of Rochester participated in the two experiments (fourteen participants in each experiment). All participants had normal or corrected-to-normal vision.

Apparatus

Subjects were seated 40 cm from a flat-screen 20 inch (diagonal measure) CRT monitor set to a resolution of 1280 × 1024 pixels. Subjects’ heads were kept in a fixed location relative to the monitor using a chin rest. During the experiment, subjects also wore a head-mounted eye tracker (EyeLink II; SR Research) that recorded gaze position at 250 Hz. The experimental software was written to ensure that subjects maintained stable fixation on a central cross for the duration of each trial. Trials where eye movements were detected were discarded and repeated during the experiment.

Procedure

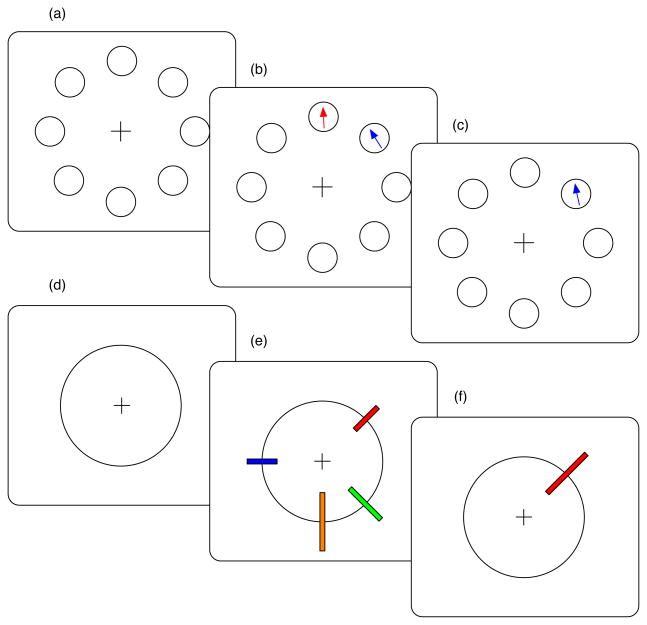
For the orientation experiment, at the start of each trial, subjects were shown a screen containing an array of eight small circles evenly spaced and equidistant from a central fixation cross (see Figure 4a). The circles were located 4 cm from the fixation point, resulting in an eccentricity of ~ 5.5 degrees of visual angle. Subjects were instructed to maintain steady fixation on the fixation cross for the duration of each trial. After 250 ms, a stimulus array was displayed (Figure 4b). This display consisted of a varying number of colored arrows (length = 1.75 cm), each arrow presented inside one of the small circles. The arrows were shown at random angular orientations drawn from a Gaussian distribution³. The mean orientation of the arrows was zero degrees (defined as pointing to the top of the display). On different trials, the number of arrows varied, using set sizes of n = 1, 2, 4, or 8 items. The trial order of the different set sizes was randomized subject to the constraint that each condition was presented an equal number of times. The arrows were uniquely colored and presented against a gray background, using the set (red, orange, yellow, green, blue, purple, brown, and white). The mapping of colors to locations was randomly determined for each participant but remained constant across trials. Subjects were instructed to memorize the orientation of each arrow. This stimulus presentation duration lasted for 500 ms, after which the display was blanked for an interval lasting 500 ms.

Figure 4.

Illustration of the experimental stimuli. (a–c): Orientation experiment. (d–f): Line length experiment. (a) Subjects were shown an array of eight small circles, evenly spaced and equidistant from a central fixation point. (b) A varying number of colored oriented arrows were presented for 500 ms. (c) After a 500 ms blank retention interval, subjects were shown a display containing just one of the original arrows. Subjects were asked to decide if the colored arrow had been rotated clockwise or counterclockwise from its previous orientation. For the line length experiment (d–f), the task was similar, except subjects memorized the length of colored line segments and were asked to decide if the probe item had been increased or decreased in length relative to its previous size.

After the memory retention interval, subjects were shown a display containing just one of the original arrows (Figure 4c). The orientation of this arrow was always different from its previous orientation, and on different trials was perturbed by an amount drawn from the set {−40, −20, −10, −2.5, +2.5, +10, +20, or + 40} degrees, where positive perturbations correspond to rotating the arrow clockwise. The task for the participant was to decide whether the arrow had been rotated clockwise or counterclockwise relative to its previous orientation. Participants responded by pressing one of two keys on a standard keyboard, depending on the direction of the perturbation. Participants were then given feedback regarding the correctness of their choice.

The variance of the Gaussian distribution governing the orientation of the arrows was manipulated as a within-subject condition. Participants completed four sessions of the experiment on separate days. On two consecutive days (either the first two or the last two), the arrows were drawn from a Gaussian distribution with low variance (SD = 15 degrees), while on the other two sessions the Gaussian distribution used a high variance (SD = 60 degrees). The order of the two variance conditions was counterbalanced across subjects.

In a separate experiment, participants were tested on their memory for the length of line segments. In the line length experiment, the initial display consisted of a single large circle (radius = 5 cm), and a fixation cross located at the center of the screen (Figure 4d). After 250 ms, a stimulus array was shown. The stimuli consisted of colored line segments of varying lengths (width = 0.5 cm), presented so that the midpoint of each line segment was located on the circle, and the line segments were oriented in a radial fashion (see Figure 4e). As with the orientation experiment, on different trials the set size varied, in the range of n = 1, 2, 4, or 8 items. On a given trial the the locations for the midpoints of the line segments were randomly selected from a fixed set of 8 possible locations evenly spaced around the circle. The set of colors for the line segments was the same as for the orientation experiment.

After a 500 ms presentation interval, the screen was blanked for 500 ms. Participants were then shown a single line segment, chosen randomly from the original set (Figure 4f). The length of this line segment was perturbed, by an amount drawn from the set {−1, −0.5, −0.25, −0.075, +0.075, +0.25, +0.5, or + 1} cm. Participants had to report whether the line segment was longer or shorter relative to its original length.

The lengths of the line segments were drawn from a log-normal distribution. A log-normal distribution is a continuous probability distribution where the logarithm of its samples follow a Gaussian distribution with a given mean and variance. A log-normal distribution was used for this experiment as it is known that perceptual discriminability of line length is proportional to length (Tuduscius & Nider, 2010), indicating a logarithmic relationship between physical and perceived stimulus magnitude (as follows from the Weber-Fechner law). By defining a log-normal distribution over stimulus features, the resulting distribution of perceived line lengths can reasonably be assumed to follow a Gaussian distribution, simplifying the model analysis. The mean parameter of the log-normal distribution was 1.18 (log transformed value, this results in a mean physical line length of ~ 3.3 cm). The standard deviation parameter was manipulated as a within-subject condition. During two consecutive sessions, the standard deviation was 0.0748 (low variance condition), while in the other two sessions the standard deviation was four times as high (high variance condition, SD = 0.299). The order of the variance conditions was counterbalanced across subjects.

For both experiments, participants completed 56 trials in each of 64 conditions (4 set sizes × 8 perturbation magnitudes × 2 variance conditions), for a total of 3,584 trials per subject over the course of four 1-hour sessions conducted on separate days.

Results

Figure 5 plots the proportion of trials answered correctly as a function of set size and signal variance condition. A 2 × 4 (variance × set size condition) repeated measures ANOVA was conducted in order to determine whether performance varied across different conditions of each experiment. For the orientation experiment, analysis of variance indicated a significant main effect of set size (F_(3,39) = 171.79, p < 0.001), with performance decreasing as the set size increased. The main effect of variance condition was also significant (F_(1,13) = 162.85, p < 0.001), with performance worse in the high-variance conditions of experiment. The interaction effect was also significant (F_(3,39) = 48.14, p < 0.001), due to the fact that performance decreased more with increasing set size in the high variance condition, compared to the low variance condition. The results for the line length experiment followed a similar pattern. Both the main effect of set size (F_(3,39) = 60.027, p < 0.001) and variance condition (F_(1,13) = 88.7, p < 0.001) were found to be significant, as well as the interaction of set size and variance condition (F_(3,39) = 12.081, p < 0.001).

Figure 5.

Proportion of trials answered correctly as a function of set size and variance condition. The left plot shows data from the orientation experiment, while the right plot is from the line length experiment. Each plot also shows the performance on a randomly selected subset of trials from the high variance condition (plotted using diagonally shaded bars), chosen to exactly match the stimulus distribution of the low variance condition. See text for details. Error bars correspond to 95% confidence intervals around the mean proportion correct.

The empirical results support the prediction that performance should be worse in the high variance conditions of the experiments. However, in comparing performance in the low and high variance conditions, it is necessary to rule out several alternative explanations, unrelated to an information-theoretic account, that may also account for the decrease in performance under high stimulus variance conditions. In both experiments, stimuli in the high variance condition were farther from the mean value, on average, compared to the low variance condition. For judgment of line length, it is known that longer stimuli are harder to discriminate (Tuduscius & Nider, 2010), and the same may hold true for the orientation experiment if subjects coded the stimuli in terms of their angular distance from the mean orientation. Therefore performance might be expected to be worse in the high variance condition because of poorer sensory discrimination, and not because of a limited-capacity memory system.

To address this possible confound, a subset of trials was extracted from the high variance condition where the distribution of line lengths or orientations for the tested items was perfectly matched to the distribution of features in the low variance condition⁴. When comparing performance of the low variance trials and the subsampled high variance trials, a perceptual discrimination account no longer predicts any performance difference (since the two conditions have an identical distribution of feature values). However, the ideal observer analysis still predicts that performance should be worse on the subsampled high variance trials compared to the true low variance condition. The intuition for this is in adapting the memory system to encoding higher variance features, the same fixed capacity must allow for coding stimuli over a wider range of values, leaving lower precision for any individual stimulus item. As a result, the information-theoretic account predicts that performance should be worse even when examining a low variance subsample of the high variance condition.

The diagonally-shaded bars in Figure 5 show the mean proportion correct in each set size condition for a low-variance subsample from the high variance condition. As predicted by the information theoretic account, performance on these subsampled trials is significantly worse than in the low variance condition for the orientation (F_(1,13) = 51.581, p < 0.001) and line length (F_(1,13) = 38.395, p < 0.001) experiments. Hence, the lower performance in the high variance condition cannot be attributed to any perceptual properties of the task unique to the high variance condition.

In both experiments, the probe items were obtained by adding positive or negative perturbations to features drawn from probability distributions with fixed variance. Because of this property, subjects could guess at above-chance levels by adopting the following strategy: if the orientation or line length of the probe item is greater than the mean value, report a positive perturbation. The logic of this strategy is that probe items with feature values greater than the mean are more likely to have been perturbed positively than negatively. This strategy would be expected to be more successful in the low variance condition (although still well below empirically observed performance), because large positive or negative perturbations would be more distinguishable from random trial-to-trial variation in the low variance condition compared to the high variance condition. However, the empirical data render an account based solely on this guessing strategy unlikely. Existing item limit models of visual memory generally assume that the limit is at least two items. Hence, these models predict that it is unlikely that responses in the low set size conditions (one or two items) reflect guesses made by participants. Therefore, a guessing explanation predicts no performance difference between variance conditions at low set sizes, while the information-theoretic account still predicts a performance decrement in the high variance condition. Consistent with the information-theoretic account, performance was worse in the high variance condition at set sizes of one and two items; statistical test results are given in Table 1.

Table 1.

Statistical comparison of proportion of trials correct in the low versus high variance condition of each experiment at low set sizes. All tests reported are two-sided paired t-tests with 13 degrees of freedom.

Experiment and set size	Mean difference	t	p
Orientation
N = 1	0.035	3.35**	.005
N = 2	0.074	7.64***	< 0.001
Line length
N = 1	0.057	3.9**	.002
N = 2	0.070	8.32**	< 0.001

Note:

^**p < .01.

^***p < .001.

It remains possible that the difference in performance between the two variance conditions is due to subjects adopting different response strategies in the two conditions. However, the design of the present experiments, as well as the results obtained, render any explanation for the variance effect based solely on strategy difference in the two conditions unlikely. First, all subjects completed both variance conditions, so if subjects adopted a particular suboptimal strategy in one session, it would likely carry over to their performance in subsequent sessions. Second, given that human performance conforms to the predictions of a limited capacity, but optimal memory system, if subjects in fact adopted suboptimal or heuristic decision strategies in the different variance conditions, it seems inescapable that these strategies would have to at least approximate the behavior of a near-optimal memory system.

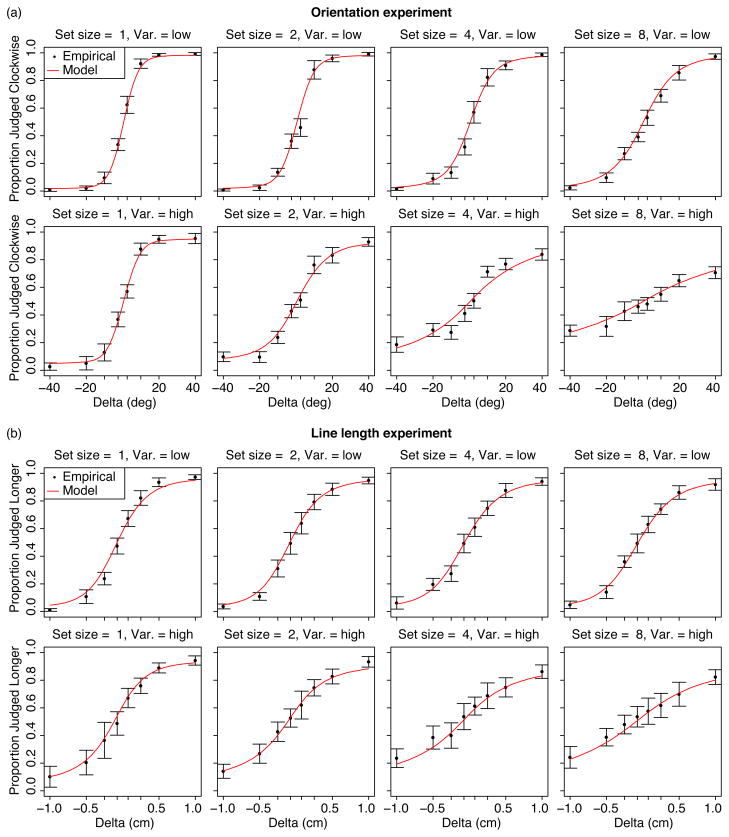
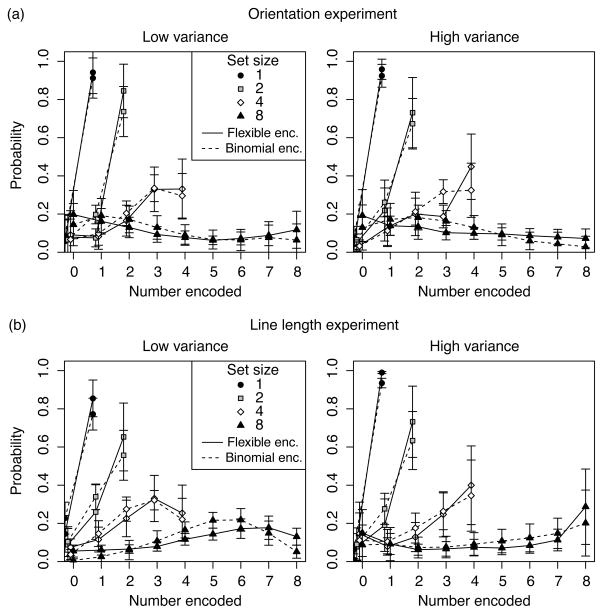
Figure 6 shows the proportion of test items judged as positively perturbed as a function of the perturbation added to the feature value. Positive values correspond to clockwise perturbations in the orientation experiment, and increases in length for the line length experiment. Data are plotted separately for each set size (varying across columns) and signal variance condition (varying across rows). As expected, the probability of judging the perturbation to be positive increased in monotonic fashion with the actual perturbation. However, less obvious is how response probability should vary with increasing set size or feature variance. As a more fine-grained assessment of human performance, we fit to the data psychometric functions that assume that the empirical data consists of a mixture of two response types: trials where the probed item was stored in memory and response probability is assumed to follow a cumulative Gaussian function of perturbation magnitude, and trials where the probed item was not stored and responses are made randomly. The key parameters of the psychometric function are the proportion of random responses, and the slope of the Gaussian cumulative function evaluated at threshold (where threshold is defined as the perturbation magnitude resulting in a 50% probability of reporting a positive perturbation).

Figure 6.

Proportion of trials judged as perturbed positively as a function of true perturbation, for each condition of the experiment. Human data is indicated by black marker points; error bars indicate 95% confidence intervals. The smooth curves shows the predictions of the flexible encoding model. (a) Data from the position experiment. (b) Data from the orientation experiment.

These parameters of psychometric performance have been closely scrutinized for evidence regarding the existence of item limits in visual working memory (Zhang & Luck, 2008; D. E. Anderson et al., 2011; Bays et al., 2009; Cowan & Rouder, 2009; Thiele, Pratte, & Rouder, 2011). Changes in the slope of the psychometric function indicate changes in the precision with which items are stored in VWM; therefore by examining how the psychometric slope changes across set sizes it is possible to examine the effect of storing more items on the precision of each memory representation. Existing item limit models predict that the psychometric slope should reach a plateau and remain constant once the set size exceeds the available number of slots in visual working memory. Beyond the item limit, increasing the set size should not influence the precision with which items are stored, but rather only impact the probability that the probe item was encoded during stimulus presentation. The continuous resource model, on the other hand, predicts that precision should monotonically decrease with increasing set size. Further, since all items are assumed to be encoded, the continuous resource model predicts that the lapse rate should equal zero for all set sizes. However, it has been demonstrated that estimated lapse rates can be nearly zero when the experimental design allows subjects to make educated guesses, even if not all items were encoded in memory (Thiele et al., 2011). Consequently, finding a low estimated lapse rate does not decisively rule out item limit models.

We estimated parameters of the psychometric function using a hierarchical Bayesian model. Bayesian inference proceeds by placing prior distributions over each parameter and inferring posterior probability distributions from the available data. In a typical (non-hierarchical) analysis, each subject is assumed to be independent; therefore, the parameter estimates for one subject do not inform the estimates for other subjects. A hierarchical model extends this approach by assuming that the variability between subjects is structured: the distribution of subject-specific parameters are assumed to follow a population-level distribution. This dependency structure increases statistical power and reduces the influence of outliers in parameter estimation (Rouder, Sun, Speckman, Lu, & Zhou, 2003; Morey, 2011) and can be a valuable tool for investigating individual differences among subjects (Navarro, Griffiths, Steyvers, & Lee, 2006). A tutorial introduction to hierarchical Bayesian models as applied to psychological research can be found in (Rouder & Lu, 2005). Implementation details of the psychometric function and parameter estimation are provided in the supplemental material.

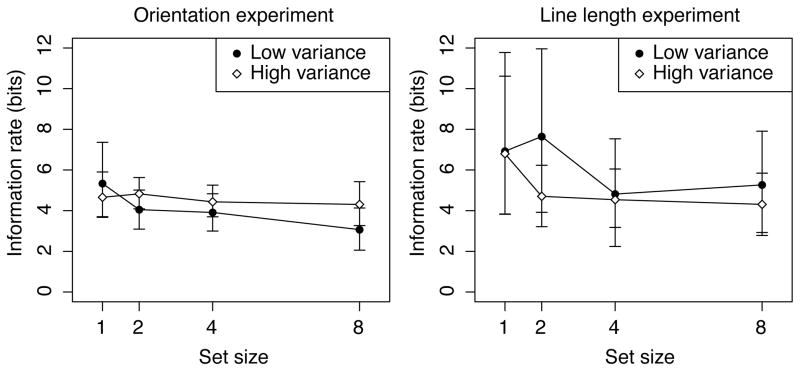
Figure 7 plots the estimated mean psychometric slope and lapse rate parameters. For both experiments, the slope is lower in the high variance condition—this indicates that increasing the variance of features in the environment led to a decrease in the precision of memory representations. Additionally, the precision of memory representations decreased with increasing set size. It is also noteworthy that the results contain aspects that are partially inconsistent with both continuous resource and item limit models of visual working memory. In the orientation experiment, the psychometric slope decreased from set size 4 to set size 8 in both variance conditions⁵. This finding is inconsistent with item limit models that assume that subjects can encode a maximum of 3–4 items (the typical item limit reported, though individuals may exhibit variation in item capacity; Vogel & Machizawa, 2004; Rouder et al., 2008). Increasing the set size beyond the item limit should have no effect on the precision of memory representations, and should therefore not effect the slope of the psychometric function. At the same time, the results are inconsistent with the continuous resource model, since the high variance condition of the orientation experiment shows that the psychometric lapse rate increases at large set sizes. In the line length experiment, there was no evidence for a decrease in slope beyond a set size of 4 items, and the estimated lapse rate was near zero for all conditions.

Figure 7.

(a) Parameters of the psychometric function fit to empirical data (solid lines) and model-generated data (dashed lines) from the orientation experiment. Left panel: Estimated slope of the psychometric function. Right panel: Estimated psychometric lapse rate. (b) Corresponding parameter estimates for the line length experiment. Model data is generated from the flexible encoding model. All error bars indicate 95% highest-density credible intervals.

For the largest set size, and high variance conditions of both experiments, the estimated slope parameters were found to be highly correlated with the corresponding lapse rate parameters. In other words, when the psychometric function is nearly flat, the empirical data do not unambiguously resolve both parameters. For the line length experiment, the correlation between slope and lapse rate was r² = 0.73 (set size 8, high variance condition), and in the orientation experiment r² = 0.65. Model fitting techniques that produce only a single set of best-fitting parameters (such as the procedure reported in (Zhang & Luck, 2008) and (D. E. Anderson et al., 2011)) fail to account for these correlations, and may potentially give misleading conclusions. However, as a Bayesian analysis provides a joint posterior distribution over both parameters, taking into account uncertainty in their values, the conclusions drawn with respect to the decrease in slope remain valid, regardless of the correlation with the lapse parameter.

A further property of the ideal observer model is that it predicts that memory representations should be biased. Since memory retrieval is assumed to be a process of decoding a noise-corrupted representation, the optimal Bayesian solution is to combine the noisy memory information available on a given trial with prior knowledge of the statistics of the relevant visual feature. As a result, the ideal observer model predicts that memory representations should be biased towards the mean feature value, and previous experiments have also demonstrated the existence of biased memory representations (Brady & Alvarez, 2011). However, the amount of bias should also depend on the actual stimulus on a given trial: visual features that are outliers (farther from the mean value) should be more strongly biased in absolute terms compared to features that are more typical (closer to the mean). This implies that when tested on an line segment (in the line length experiment) that was initially much longer than average, the subject should be more likely to report that the probe stimulus was increased in length rather than decreased.

Additionally, the amount of bias might also depend on the number of items that are concurrently stored in memory. When many items are encoded, fewer resources may be allocated to each item, and therefore the encoding process would be expected to introduce more noise into the representation. In this case, the optimal Bayesian solution is to give more weight to the prior distribution over features. As a result, the ideal observer model predicts that memory representations should be more strongly biased in the high set size conditions, where more items are likely to be encoded simultaneously. The predicted effects of feature variance on bias are less straightforward: with higher feature variance, the prior distribution is less informative; on this basis one would expect a smaller amount of bias. However, memory representations are also less precise in the high variance condition leading to an increased reliance on the prior. These two factors counterbalance each other, and therefore the model does not make a clear-cut prediction regarding the amount of bias in the two variance conditions of the experiment (further details are given in the supplemental material).

To investigate the extent to which VWM was biased in the experiments, we binned the response data according to the initial feature value (orientation or line length) of the to-be-tested stimulus item into ten equal quantiles. This binning procedure was performed separately for each set size and variance condition. The estimated response bias for a subject in a particular stimulus quantile, set size, and variance condition was computed as

$$\text{Response}\text{bias}=\frac{1}{N}\sum _{i=1}^N\left[Z_i-{\overline{Z}}^{({\mathrm{\Delta }}_i)}\right],$$ (6)

where N is the number of trials where the initial orientation or line length falls into the current quantile, and Z_i is the binary response (1 or 0) indicating whether the participant reported a positive perturbation on on trial i. The variable Δ_i is the actual perturbation level on trial i, and Z̄^(Δ_i) indicates the average proportion of trials where the subject reported a positive perturbation when the perturbation level was Δ_i, with the average computed across all set sizes, variance conditions, and initial feature values. This measure of bias effectively subtracts out the effect of the perturbation on response probability, to focus directly on the effect of the initial feature value, set size, and variance condition on the tendency to report a positive perturbation. According to this measure, positive values of bias indicate an exaggerated tendency to report a positive perturbation, relative to the average for that subject when computed across all set sizes and variance conditions.

If VWM is unbiased, then the estimated response bias should be zero for all conditions, regardless of line length or orientation. By contrast, the ideal observer model predicts that bias should increase as stimuli are more distant from the mean value. Further, if the amount of memory resources allocated to each item depends on the number of items in a scene (as assumed by both the continuous resource and the slots+averaging model), then the magnitude of the bias should increase with increasing set size. The results of this analysis are shown in Figure 8, where the data have been binned into 10 equal quantiles according to the initial feature value of the tested item. It is apparent from the figure that response bias strongly depends on the magnitude of the visual feature, but also depends strongly on the set size condition. Both effects are directly predicted by an optimal memory system that attempts to accurately store visual features in the presence of encoding noise.

Figure 8.

Relative response bias, defined as the tendency to report a positive perturbation, as a function of the initial feature value of the to-be-tested item, set size, and variance condition. Feature values are binned into ten equal quantiles (deciles), and response bias is computed separately for each subject, quantile and experimental condition (set size and feature variance). (a) Data from the orientation experiment. (b) Data from the line length experiment. Error bars indicate 95% confidence intervals, averaging across subjects.

In summary, the empirical results support several key predictions of the ideal observer analysis. First, it was shown that performance decreased as the variance of features in the environment increased. This predicted change in performance is a fundamental consequence of results derived from rate–distortion theory, but is not predicted by existing models of visual working memory. The results also demonstrated that memory representations appear to be biased in a manner predicted by the ideal observer analysis. Such biases are the hallmark of a system that is appropriately adapted to the statistics of features in the environment. Finally, the estimated parameters of the psychometric function produced results at least partially inconsistent with both item limit and continuous resource models. In the next section, we compare several models developed within the framework of the ideal observer analysis to determine which most accurately accounts for the specific pattern of results obtained in the two experiments.

Ideal observer analysis applied to empirical data

In order to generate quantitative predictions for the data from the experiments, it is necessary to specify how items are selected to be encoded in visual working memory (for example, whether there is a fixed item limit, and how capacity is divided among encoded items). Rather than defining a single model, the ideal observer analysis instead serves as the theoretical foundation for a family of related models. Each of the models in this family are linked through their use of rate–distortion theory to predict optimal performance for a given total information capacity, and allocation of that capacity among items. In this section, we also consider the ability of two non-information-theoretic models—existing versions of the continuous resource (Wilken & Ma, 2004; Bays & Husain, 2008) and slots+averaging (Zhang & Luck, 2008; Cowan & Rouder, 2009) models—to account for the empirical data.

Information-theoretic models

For all models considered in this section, the response on each trial (assuming the probe item was encoded in memory) is obtained by comparing the sensory noise corrupted probe stimulus, to the memory estimate of the original item. If y_s is the sensory observation of the probe stimulus, and x̂ is the optimal memory reconstruction computed according to Equation (5), then the decision rule is simply

$$\text{Decision}=\{\begin{array}{cc}+,& (y_s-\widehat{x})>0,\\ -,& (y_s-\widehat{x})<0,\end{array}$$ (7)

where + is a response indicating a positive perturbation (clockwise in the orientation experiment, or longer in the line length experiment). The supplementary material provides a proof that this is the optimal decision rule for the psychophysical experiments. While all models adopt this same decision rule, it is possible to define models that differ in terms of how many items are encoded, and how memory capacity is divided among encoded items.

Information-theoretic continuous resource model

If memory capacity is given by R bits and there are n items to store in VWM, then a simple approach would be to store all n items, encoding each with an information rate of R/n bits. As will be shown later, this is also the optimal allocation strategy for the particular experiments reported here. This model predicts that as the number of items stored in memory increases, the precision with which each item is encoded will necessarily decrease. This would correspond to an information-theoretic reinterpretation of a continuous resource model (Palmer, 1990; Wilken & Ma, 2004; Bays & Husain, 2008), which evenly distributes a continuous pool of resources among all visual features in a scene. However, rather than being abstractly specified, the notion of a shared resource is now precisely defined in terms of bits of capacity. This allows the model to predict absolute levels of performance, whereas existing instantiations of the continuous resource model can only predict relative performance across different set sizes. Further, the information-theoretic implementation of the model allows it to directly predict performance differences between the two variance conditions of the experiments, whereas existing formulations of this model would predict no effect of feature variance on performance.

Information-theoretic slots+averaging model

An alternative possibility is that the visual working memory system encodes only a limited subset of items. Many existing theories of visual working memory assume that there is an upper limit of ~3–4 items that can be stored simultaneously (e.g., Cowan, 2001). Such a model can be implemented in the rate–distortion framework by assuming that there are separate distinct slots, each with a capacity of R bits, where R is independent of the number of items stored. Once all the available slots are filled, no additional items are encoded. The slots+averaging model (Zhang & Luck, 2008; Cowan & Rouder, 2009) is a recent theory of visual working memory that similarly assumes an item limit, but allows any unused slots to ”double up”, so that multiple slots may encode the same item. We derived an information-theoretic version of this model by assuming that each encoded item receives j × R bits of capacity, where j is the number of slots assigned to that particular item, and R is the information capacity of a single slot. For example, if an item is stored in two slots, then it is encoded with 2 × R bits. According to this model, if a scene contains more objects than available slots, each slot encodes a unique object. If the scene contains fewer objects than available slots, each object is encoded in one slot, and the remaining slots are randomly assigned to objects, so that there is a chance that the same object may be encoded in two or more slots.

The information-theoretic slots+averaging model has two distinct advantages over standard (non information-theoretic) item limit models. First, the information-theoretic model is able to quantify, in task-independent fashion, the precision with which a single slot can represent an object or visual feature. Note that while existing discrete slot models are largely silent on the issue of capacity limits for individual slots, rate–distortion theory makes transparent that such limits must necessarily exist, and further enables a means of estimating this capacity. If human performance is only weakly constrained by the capacity limits of individual slots, the information-theoretic discrete slot model would be able to reveal this as well. Second, the information-theoretic implementation predicts that memory precision for stored items should be worse in the high variance condition, even assuming a constant number of slots and fixed storage capacity per slot. To account for the effects of the variance manipulation, existing item limit models would need to postulate an additional constraint or mechanism.

Stochastic encoding models

While the slots+averaging model allows unused slots to be randomly assigned to objects in a scene, resulting in higher-precision encodings of some items, the model in its simplest form still assumes that the total number of items encoded on each trial is fixed and deterministic. Previous discussions of item limit models have raised the possibility that there is some amount of trial-to-trial variability in the number of items encoded (e.g., Vogel et al., 2001; Luck, 2008, p. 56), but have not attempted to estimate the magnitude of variability present in behavioral data for individual subjects. However, inferring the magnitude of this variability is critical in evaluating whether there is a strong upper limit on the number of items that can be maintained in VWM. For example, it is possible that VWM has a capacity limit of 8 items, but on each trial individuals encode some random number of items between 0 and 8, chosen equally often. In this case, an item limit model fit to such a data set would lead to an estimated item limit of 4 items (the average number encoded), when in fact the true item limit is twice as high. Similarly, it is also possible for the average number of encoded items to be in the range of 3–4, without requiring any upper limit in VWM.

Because of this potential confound, it is necessary to consider encoding models where there is an explicit probability distribution over the number of items encoded in memory, rather than estimating only the average number of items stored. By directly estimating encoding variability, it is possible to assess the strength of evidence for an upper limit on VWM representations. A simple model in this family is one that assumes that there is a constant probability of encoding each additional item; this leads to a binomial distribution over the number of encoded items on a given trial. In the present implementation, we allow for the possibility that this encoding probability differs across set size and variance conditions of the experiment. This model—referred to as the binomial encoding model—requires estimating one parameter (the encoding probability) of the binomial distribution in each condition. While this model allows for trial-to-trial variability in encoding, it does not require an upper limit on the number of items that can simultaneously be stored. On trials where more items are encoded, a central shared capacity is divided more thinly among each item.

The binomial encoding model allows considerable variability in the number of items encoded. However, it still assumes that the distribution over the number of encoded items follows a particular parametric form (ie, a binomial distribution). Therefore, we also consider a model in which the distribution over the number of encoded items is completely unconstrained. That is to say, we treat the probabilities of encoding 0 . . . n items in each condition as free parameters to be estimated from the data. This “flexible encoding” model includes as special cases both the discrete item limit, and the continuous resource models. For example, a discrete item limit model predicts that subjects always encode 4 items (assuming a set size ≥ 4 items). This is captured by an encoding distribution that selects 4 items with probability 1, assigning 0 probability to the possibility of encoding more or fewer items. Similarly, the continuous resource model predicts that individuals encode all stimulus items in the display with probability 1. Thus, both encoding mechanisms are special cases of the flexible encoding model. By considering a model flexible enough to encompass a range of possibilities, it is possible to gain insight as to the properties of VWM by examining the resulting parameter estimates from the model. For both the binomial model and the flexible encoding model, we assume that the capacity is evenly divided among all encoded items, so that if there are n items encoded on a particular trial, and R bits of total capacity, each encoded item receives R/n bits of capacity.

Both the flexible encoding model, and the binomial encoding model, represent possible instantiations of the hypothesis that encoding variability plays a significant role in human VWM performance. Further, both models allow for trial-to-trial variability in the number of encoded items without assuming an upper item limit on storage. It is possible to imagine a number of other plausible models in this family. However, our primary concern lies in estimating the relative magnitude of encoding variability in VWM performance, compared to existing item limit and continuous resource models which assume a comparatively minimal role for encoding variability.

Decision rule when the probe item was not encoded in memory

For all of the models except the continuous resource model, an additional detail needs to be specified regarding how responses are generated on trials when the probed item was not encoded during the initial stimulus presentation (the continuous resource model assumes that all items are encoded on each trial). If an item was not encoded in memory, then subjects could simply guess if tested on that item. However, the design of the experiments allows subjects to make above-chance guesses based purely on the statistics of the probe stimulus. To account for this possibility, if tested on an item not encoded in memory, the models computed the probability of a positive or negative perturbation based solely on the probe stimulus and knowledge of the task (the discrete perturbation levels, and the mean and variance of the feature values). We define P(Δ > 0 | y_s) as the probability that a probe item was perturbed positively, given only the observation of the probe stimulus (the equation for computing this is provided in the supplemental material). The “optimal guessing strategy” is to respond that a positive perturbation occurred whenever P(Δ > 0 | y_s) > 0.5. For the present experiments, this occurs whenever y_s is perceived to be greater than the mean orientation or line length over visual features. This leads to the optimal guessing strategy

$$\text{Decision}=\{\begin{array}{cc}+,& (y_s-{\mu }_w)>0,\\ -,& (y_s-{\mu }_w)<0.\end{array}$$ (8)

The similarity between Equations (8) and (7) reveals that the optimal guessing strategy is in fact a limiting case of the ideal observer model when memory capacity is reduced to zero. In this case, the optimal memory estimate x̂ is simply the mean of the distribution over features, μ_w.

Individual subjects in the experiment may differ in terms of their use of this guessing strategy. It is also possible that subjects may probability match (Myers, 1976): if the probability that the probe item was perturbed positively is 0.7, a probability matching subject will respond with a positive perturbation only 70% of the time. To account for these possibilities, the probability of reporting a positive perturbation on trials when the probe item was not encoded is modeled as

$$P(+\mid y_s)=\frac{P{(\mathrm{\Delta }>0\mid y_s)}^{\psi }}{P{(\mathrm{\Delta }>0\mid y_s)}^{\psi }+{(1-P(\mathrm{\Delta }>0\mid y_s))}^{\psi }}.$$ (9)

The parameter ψ controls the extent to which subjects make educated guesses: when ψ = 0, guesses are made completely randomly; when ψ = 1 probability matching results, and as ψ → ∞ the subject approaches optimal guessing performance.

Non-information-theoretic models

We also evaluated non-information-theoretic versions of the continuous resource and slots+averaging models. For the non-information-theoretic continuous resource model, memory representations are corrupted by Gaussian noise, where the standard deviation of the noise varies as a general power function of the set size. The exponent of the power function represents an additional free parameter in this model, compared to its information-theoretic equivalent. To maintain consistency with the information-theoretic version, we also included a sensory noise parameter that is constant across set sizes (the model described by Bays and Husain (2008) did not explicitly model sensory noise).

For the non-information-theoretic slots+averaging model, each slot encodes an item with added Gaussian noise where the noise variance is constant regardless of the number of slots or items encoded in memory. If an object is encoded in multiple slots, memory error is minimized by averaging the stored representation in each slot. We also included a sensory noise parameter in this model to maintain consistency with its information-theoretic counterpart. For both non-information-theoretic models, there is no predicted performance difference between the low and high variance conditions when tested on items that were encoded in memory. The non-information-theoretic slots+averaging model does allow for a performance difference between the low and high variance condition due to the predicted poorer performance when tested on non-encoded items.

Summary of models

For all models, we also included a lapse component and overall bias term. On some percentage of trials, given by the lapse parameter, the response is modeled as being generated randomly regardless of whether it was encoded in memory. This was included to allow for the possibility that subjects occasionally press the unintended response key or exhibit lapses in attention or motivation. Failing to account for the possibility of such lapses can lead to large biases in the parameters estimated from a model, especially on trials with small set size or large perturbations (for a more extensive discussion of this issue, see Rouder et al., 2008; Morey, 2011). The bias term is included to allow the possibility that subjects incorrectly estimate the mean of the distribution over feature values in the experiments or exhibit an overall bias towards reporting positive or negative perturbations. In evaluating several of the models, we found that the model fit was slightly improved by allowing the lapse rate to differ across variance conditions of the experiment. Consequently we report results for all models allowing separate lapse rates in the low and high variance conditions.

To summarize, we have proposed six different models of the allocation of capacity when multiple items must be stored in visual working memory. Four of the models (continuous resource, slots+averaging, binomial encoding, and flexible encoding) reflect a range of possible memory systems, but all share the underlying information-theoretic framework that relates capacity, defined in bits, to the precision of memory representations. The latter two models, the binomial encoding and flexible encoding models, are two possible instantiations of the idea that accounting for encoding variability is a critical factor in explaining VWM performance. We also evaluated two standard (non-information-theoretic) models as a further test of the contribution of the ideal observer analysis. In this section, the goal is to evaluate each model in terms of its ability to account for the observed human performance.

We estimated the parameters for each model using Bayesian inference (see Kruschke, 2011, for an introduction to Bayesian data analysis techniques). Complete details regarding the implementation of the models and parameter estimation procedure are provided in the supplemental material.

Model results

To determine which model was best able to account for the empirical data, each model was evaluated using the deviance information criterion (DIC; Gilks et al., 1996) score. DIC is a technique for selecting between models that balances goodness of fit (the mean log-likelihood score for the model) with a penalty term related to the model’s complexity. This penalty term prevents the selection of models with many degrees of freedom that overfit the available data. Figure 9 shows the calculated DIC score, relative to the best-fitting model in each experiment. Smaller DIC scores indicate models that are better able to fit the data after adjusting for model complexity. In both experiments, the best fitting model is the flexible encoding model, though the binomial encoding model performs nearly as well in comparison to the remaining models ⁶. It is notable that the two best-fitting models both assume that subjects sometimes encode more items with lower precision, and sometimes encode fewer items with greater precision. By contrast, both item limit and the continuous resource models assume that a constant number of items will be encoded in VWM on each trial (either the entire array, in the continuous resource model, or up to the slot limit in item limit models).

Figure 9.

Comparison of alternative memory encoding mechanisms, evaluated according to DIC score. The left figure shows the results for the orientation experiment. The right figure shows the line length experiment. Lower DIC scores indicate models that better fit the data. The numbers above each bar indicate the DIC score relative to the best-fitting model in each experiment.

The worst-fitting model in both experiments is the non-information-theoretic continuous resource model. This model fits the data so poorly since, unlike all the other models, it predicts no difference in performance between the high and low variance conditions. The non-information-theoretic slots+averaging model is able to predict lower performance in the high variance condition, but only on trials where the probe item was not encoded in memory. Therefore, it cannot account for the empirically observed performance decrement at low set sizes (Table 1) unless it is assumed that the slot capacity is limited to a single item. Further, in both experiments, the information-theoretic models substantially outperform their non-information-theoretic counterparts, despite having the same number, or fewer parameters.

Figure 6 shows the resulting fit of the flexible encoding model to the empirical data. The model fits were obtained by averaging over the model predictions for each individual participant. As can be seen by inspection of the figure, the empirical and model data are in close quantitative agreement (in nearly all cases, the model predictions fall within the confidence intervals for the observed human data). As a more rigorous test of the flexible encoding model’s ability to account for the human data, we also generated simulated data sets for both experiments using the model. These data sets were obtained by running the model through the exact sequence of trials and stimuli given to the human participants. Simulated responses were obtained using the mean parameter estimates for each of our participants. To reduce the variability in the model’s predictions, 10 repetitions were generated for each trial completed by a human participant. As shown in Figure 8, the flexible encoding model is able to account for the observed biases in memory. We then analyzed the model-generated data using the same psychometric function analysis that was applied to the empirical data. Figure 7 compares the estimated parameters of the psychometric functions for the human data and model-generated data. The models are able to qualitatively capture both the psychometric slope and lapse rate of human performance.

In both experiments, the flexible encoding model was able to fit the data better than the binomial encoding model when evaluated according to DIC score. We therefore examined the extent to which the predicted encoding distribution differed between the two models. Recall that the binomial encoding model assumes a particular parametric form for the encoding distribution, and thus has just one parameter (the encoding probability per item) to be estimated for each condition. Figure 10 plots the estimated probability of encoding each stimulus item according to the binomial encoding model. Under the assumption that memory encoding follows a binomial distribution with encoding probability p, and set size of n possible items, the trial-to-trial variance in the number of items encoded is given by n p (1 − p). For both experiments, the encoding probability is a decreasing function of the set size, while there is little or no difference in the encoding behavior in the two variance conditions.

Figure 10.

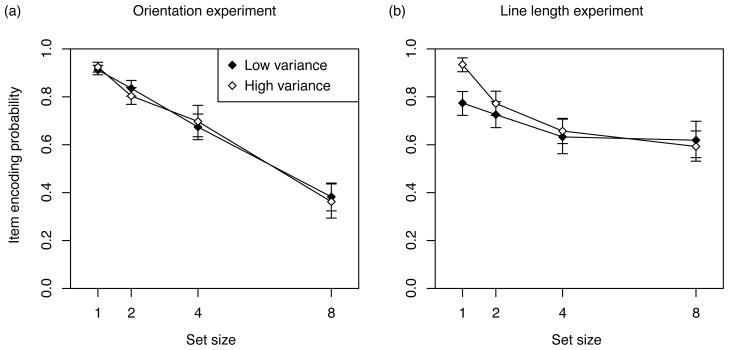
Probability of encoding each stimulus item, according to the binomial encoding model. (a) Estimates for the orientation experiment. (b) Estimates for the line length experiment. Error bars indicate 95% confidence intervals.

Compared to the binomial encoding model, the flexible encoding model is completely unconstrained in terms of its allocation, such that the probabilities of encoding 0 . . . n items in each condition are treated as free parameters. Because of this lack of constraint, the flexible encoding model could reproduce the encoding behavior predicted by the slots+averaging model, the continuous resource model, or any possible distribution over items encoded. To compare the behavior of the binomial and flexible encoding models, we computed the (binomial) encoding distributions predicted by the binomial encoding model, and compared these to the encoding distributions estimated according to the flexible encoding model. The distributions are overlaid in Figure 11. As can be seen by inspection of the figure, the two models predict a highly similar pattern of behavior, despite the fact that the flexible encoding model introduces numerous additional free parameters. Further, the inferred encoding distributions from both models are qualitatively different than would be predicted by existing item limit theories. This is not due to any constraints or assumptions of the models, as the flexible encoding model would be capable of reproducing the appearance of an item limit, if in fact the data were generated by such a process. In summary, although the flexible encoding model is favored over the binomial encoding model according to a Bayesian model comparison, a binomial encoding model where the encoding probability represents a decreasing function of set size appears to offer a concise account of the encoding process in visual working memory. However, we believe the more important result is that both models offer a significant improvement in the ability to account for human performance over existing models of visual working memory. Both models allow for substantial encoding variability, but also assume that memory precision is directly tied in trial-by-trial fashion to the number of stored representations.

Figure 11.

Estimated distribution over the number of items encoded on each trial, according to the binomial (dashed lines) and flexible (solid lines) encoding models. (a) Data from orientation experiment. (b) Data from line length experiment. Error bars indicate 95% confidence intervals.

For the information-theoretic slots+averaging model, we determined the slot limit that had the highest probability for each subject. The most common estimated item limit in both experiments was found to be 3 items. The posterior mean item limit (a measure which takes into account the uncertainty in each subject’s estimate) yields a similar result: an average of 3.87 items for the orientation experiment, and 4.22 items in the line length experiment. These results closely correspond to previous estimates of 3–4 items (Zhang & Luck, 2008; D. E. Anderson et al., 2011; Cowan, 2001; Cowan & Rouder, 2009). While the estimated item limits for the present experiments are close to previous estimates, it remains the case that a discrete item limit model offers a relatively poor account of the data compared to two alternative models that do not assume the existence of an item limit in VWM.

Table A1 (Appendix) lists the posterior mean parameter estimates and 95% credible intervals for all parameters that are common across the information-theoretic models. Within each experiment, the parameter estimates are similar for each of the models considered, suggesting that the estimates are fairly robust to potential misspecification of the encoding mechanism in VWM. Capacity is reported as total capacity measured in bits, computed for item limit models as (Capacity per slot × Number of slots).

The probability matching exponent (defined in Equation 9) is credibly different than zero in both experiments, indicating that on trials where a probed item was not encoded in memory, subjects were able to guess the correct response at above-chance levels. This result is not surprising, given that it has previously been demonstrated in a similar paradigm (Thiele et al., 2011). In the line length experiment, subject performance rather closely approximated probability matching, while in the orientation experiment performance was slightly better (ψ = 3.3 for the best-fitting model). This suggests that in the orientation experiment subjects were better able to make better use of knowledge of the distribution over features. Given that the mean orientation of arrows had a natural reference point (the mean orientation was vertical), while the mean line length was more arbitrary, it is perhaps not surprising that we find this difference between the two experiments. Future experiments might explore this result further by employing a less intuitive distribution over orientations (for example, having a mean orientation that is randomly generated for each subject), and examining the effect on the estimated probability matching exponent.

For the best fitting model (the flexible encoding model), we also examined whether the total capacity remains constant across set sizes and variance conditions. Recall that the ideal observer analysis predicts that total memory capacity should remain constant across the two variance conditions of each experiment, even though performance significantly dropped in the high variance conditions. Further, if the visual memory system shares a single pool of resources among encoded items, then the total allocated capacity should remain constant across set sizes, regardless of how many items are encoded. If, on the other hand, visual working memory does not optimally divide a central capacity among encoded items, then we might expect to find deviations in the estimated capacity in different set size or variance conditions. To examine this possibility, we modified the flexible encoding model to allow potentially different information capacities for each variance and set size condition. Because of the additional degrees of freedom introduced by allowing multiple capacity parameters, it was necessary to include hierarchical priors over the mean capacity in each experimental condition. In other words, the hierarchical model assumed that the capacity estimate for each subject in each condition was drawn from a probability distribution with a condition-specific mean, and these condition-specific mean capacities were distributed according to an over-arching distribution over capacity. This was necessary because the limited data available in each condition did not sufficiently constrain the posterior distributions over capacity when parameters were estimated independently for each subject and condition. In particular, for set sizes of 1 or 2 items, performance may be dominated by sensory noise rather than capacity limitations, making it difficult to unambiguously estimate capacity in the absence of a hierarchical prior.

Figure 12 shows the posterior mean estimated capacity in each condition of each experiment for the extended model. Comparison of the mean capacity between conditions revealed that there were no credible differences across any of the conditions (in all cases the 95% credible interval for the difference in means included zero). Although the models allowed the capacity to differ between conditions, based on the empirical data there is no evidence to suggest that total allocated memory capacity did in fact vary.

Figure 12.

Posterior mean estimates of memory capacity in different conditions of the experiments. (left) Estimated capacity in each condition of the orientation experiment. (right) Estimated capacity in the line length experiment. Error bars correspond to 95% credible intervals around the mean capacity for each condition.

Finally, although we evaluated four different information-theoretic models in terms of their ability to account for the empirical data, an additional question is which mechanism defines optimal performance for the particular experiments reported here. This analysis could potentially be informative, since if subjects were observed to behave in a manner that is substantially suboptimal for the particular task environment (for example, if encoding a limited subset of items would dramatically impair performance), it would suggest limits to the adaptability of encoding behavior across differing task environments. To answer this question, we used the mean parameter estimates from the flexible encoding model (reported in the Appendix), and generated 100,000 simulated trials in each condition from each of the models using a common set of parameter values. This allowed us to evaluate the performance level that would be achieved by each model, assuming a common sensory noise and total capacity, so that the only difference between models was in terms of the encoding mechanism.

Surprisingly, the expected performance of each allocation mechanism was extremely similar. In the orientation experiment, the slots+averaging model (with a capacity of 4 slots) would be expected to perform the worst for a given total capacity (80.6% correct), while the continuous resource model would be expected to perform the best (81.1%). Performance differences, although small, were stable across repeated simulations. The binomial and flexible encoding models were able to match the performance of the continuous resource model by encoding the entire stimulus array on each trial (mimicking the continuous resource model). Thus, for these particular experiments, encoding the entire stimulus array on each trial would be expected to achieve the highest level of performance, though only marginally out-performing other encoding strategies. A consistent ranking of models was found for the line length experiment. This does not imply that the same encoding strategy would be optimal for other tasks; the details of what defines an optimal allocation strategy are highly task dependent, though as we have shown, the drop in performance for sub-optimal encoding strategies may be surprisingly small.

Summary of model results

The model analyses reported in this section provide additional support for the ideal observer framework as a productive tool for studying and modeling limits in visual working memory. Despite the fact that performance was significantly worse in the high signal variance and the larger set size conditions, these results are naturally and concisely predicted by a model of VWM that assumes a constant overall memory capacity. In comparing different mechanisms for the allocation of this capacity, we demonstrated that the best model for the empirical data is one that assumes that there is a single memory capacity that is divided among encoded items, but allows the number of items encoded to vary from trial to trial, and across different conditions of the experiment. The model comparison results rule out basic item limit models that assume a fixed number of encoded items, but also exclude the continuous resource model that assumes all stimulus items are encoded in memory. Instead, the results indicate a VWM system that exhibits substantial variability in terms of its behavior: Subjects may sometimes encode many items with low precision, and on other trials encode a few items precisely. Further, the empirical results provide no strong evidence for a strict or universal upper limit on the number of items that may be encoded, suggesting that if there is such a limit, it may not be that powerful as an explanatory mechanism in accounting for human performance on any given trial.

Summary and Conclusions

This paper has developed an ideal observer analysis (Geisler, 2003, 2011) of human visual working memory (VWM). While it is clear from decades of research that there are strong limits on the performance of human VWM (Luck, 2008; Brady et al., 2011), the precise nature of these limits is rather poorly understood. While existing theories have posited memory encoding mechanisms intended to account for observed phenomena, the present paper applies the ideal observer framework to uncover the expected behavior of an optimally performing, but finite capacity memory system. Importantly, the nature of the capacity limit was not chosen to fit the empirical data, but rather derived a priori on the basis of results from a branch of information theory known as rate–distortion theory (Berger, 1971). Rate–distortion theory provides the theoretical bounds on performance for any capacity-limited communication channel—be it human memory or a telegraph wire—where capacity is formally defined in terms of bits.

An important contribution of the ideal observer analysis is that by defining capacity in a task-independent manner (namely, bits), the results obtained in one experiment may be used to generate quantitative predictions for other experiments in a straightforward manner. Additionally, by starting from an optimal model of VWM, the estimated capacity represents a theoretical lower bound on human memory capacity. In practice, the estimation of memory capacity from behavior is complicated by the need to simultaneously account for sensory noise, lapses in attention, as well as the mechanism by which capacity is distributed across multiple items. Even in this case, if an optimal model of performance can be defined for a given task, then it remains possible to estimate a valid lower bound on capacity. That is to say, subjects may have a higher memory capacity but are limited by other factors such as sensory noise, or use their capacity in suboptimal fashion (for example, applying a suboptimal decoder to imperfect memory representations). In this case, the ideal observer model fit to empirical data leads to a measure of the effective capacity of VWM, rather than its theoretical maximum capacity.

The ideal observer analysis does not yield a specific single model of visual working memory. Instead, it defines a theoretical framework for testing alternative models of visual memory. The central component of this framework is the realization that quantitative limits on human memory performance can be directly predicted from a known memory capacity, and conversely, a minimum memory capacity can be directly inferred from observed human performance. By applying this framework to empirical data collected across two experiments, it was possible to evaluate several alternate theories of the memory encoding process, including two existing models that have made competing claims regarding the mechanisms of visual working memory.

Information-theoretic analysis of perceptual systems is not a new approach (Attneave, 1954; Miller, 1956). One closely related area of investigation is absolute identification (Garner, 1953; Luce, Green, & Weber, 1976), where subjects are presented with a unidimensional stimulus drawn from a discrete set and must respond by identifying which item out of the set was presented. By varying the set size, it is possible to manipulate the informational demand of the task, and by measuring identification errors, one can estimate the channel capacity of the subject. Whereas absolute identification tasks examine the ability to unambiguously assign stimuli to discrete categories, rate–distortion theory as applied to visual memory instead focuses on the ability to minimize the introduction of error in storing and retrieving continuous feature values.

The present work is the first to apply rate–distortion theory as the optimal solution to problem of encoding and retrieving visual information in a capacity-limited memory system. Perhaps surprisingly, a model with only weak constraints on performance (assuming only the existence of sensory noise and a finite limit on memory capacity) was able to offer a parsimonious and quantitative account of empirical results obtained in two experiments, including the empirical validation of the predicted effects of manipulating the variance of features in the task.

Based on the results obtained in two experiments and subsequent model comparisons, we conclude that when encoding multiple items in memory, people rely on a single, fixed memory capacity that is distributed among encoded items. The empirical results and model comparisons also suggest deficiencies of two previous, but competing models of VWM. The continuous resource model (Bays & Husain, 2008) predicts that there is no upper limit on the number of items encoded in VWM, and in its existing instantiations, has assumed that people encode all stimulus items in a scene. By contrast, the slots+averaging model (Cowan & Rouder, 2009; D. E. Anderson et al., 2011) predicts that there is a fixed upper limit on the number of items that can be encoded. In the majority of instantiations of this model, the hypothesized mean capacity limit is 4 items (Cowan, 2001), although evidence suggests there may be significant variation among individuals (Vogel & Machizawa, 2004; Todd & Marois, 2005; Rouder et al., 2008). Discussions of this model have raised the possibility of trial-to-trial variability in the number of stored representations (Vogel et al., 2001; Luck, 2008), but to date, the magnitude of encoding variability has not been directly estimated in fitting item limit models to human performance.

Based on the combined data from both experiments, there is no strong evidence to support a universal item limit in VWM: the empirical results were better explained by a model that allowed for encoding variability, but assumed the absence of an item limit. At the same time, it was not found to be the case that subjects universally encode all stimulus items in a display, as predicted by existing versions of the continuous resource model. Instead, it appears that humans may exhibit substantial variability in how they allocate their memory capacity; sometimes remembering many items with low precision, and sometimes remembering a few items precisely.

Recently, a closely related model has been proposed (Van den Berg et al., 2012) in which trial-to-trial variability in encoding precision, rather than variability in the number of encoded items, was argued to be the critical factor in accounting for human memory performance. According to this variable precision model, all stimulus items are encoded, but each receives an amount of resource (equivalent in their model to precision) randomly drawn from a probability distribution, such that some stimulus items may be encoded with low precision. The variable precision model was shown to outperform traditional item-limit theories in two different experimental tasks (delayed estimation and change localization) and two different visual features (orientation and color). Like the best-fitting model for our data, the variable precision model assumes that variability in VWM, rather than the existence of a discrete item limit, accounts for the empirical facts of human performance. Thus, the two models are closely related, and gain mutual support from their success in different experimental paradigms. Further, both models are functionally similar in treating memory representations as noise-corrupted versions of physical features. While the variable precision model (Van den Berg et al., 2012) treats the magnitude of encoding noise in memory as a free parameter estimated separately for each condition, the information-theoretic framework offers a rational basis for predicting how memory precision should vary with experimental parameters (including set size, and the prior distribution of features in the environment).

Relation to other empirical results

How do the present conclusions differ from those of other recent studies of visual working memory capacity? Previous attempts at demonstrating the existence of item limits in visual working memory have focused on properties of simple psychometric functions fit to empirical data. One such property is whether the estimated slope of the psychometric function reaches a plateau with increasing set size. Item limit models predict the existence of such a plateau, since increasing the set size beyond the item limit should have no effect on the precision of memory representations. By contrast, the continuous resource model predicts that memory precision should monotonically decrease with increasing set size. In the empirical data reported here, there was limited evidence regarding the existence of a plateau in the slope of the psychometric function. The collective results from other recent studies also paint a mixed picture, with some studies showing no evidence for a plateau (Bays & Husain, 2008, supplemental material) and others showing its existence (Zhang & Luck, 2008; D. E. Anderson et al., 2011).

Several factors may limit the usefulness of this type of analysis. First, finding a plateau in group-averaged data does not imply the existence of any such effect at the level of individual subjects (Rouder et al., 2008). Second, Bays and colleagues (Bays et al., 2009, 2011) have argued that a plateau in memory precision may be accounted for by subjects misreporting the features for the wrong stimulus item, although this possibility has been challenged (D. E. Anderson et al., 2011). Third, and more importantly, it has previously been assumed that finding this effect constitutes definitive evidence for an upper limit on the number of items that may be stored in visual working memory. The present results have proved this assumption to be unfounded, since the best-fitting models were able to reproduce the main features of human psychometric performance without assuming the existence of an item limit (see also Van den Berg et al., 2012).

In comparing these empirical results to other studies, it is also important to account for the possibility that methodological differences may play a significant role. In the present experiments, subjects were given a forced choice on each trial, whereas other experiments have used a ‘cued recall’ paradigm, in which subjects choose from a continuum to indicate their response. The testing procedure used to assess visual memory has previously been shown to influence the measured sensitivity of memory (Makovski, Watson, Koutstaal, & Jiang, 2010). Other methodological differences may be important as well: in the present experiments, stimuli were presented at fixed retinal eccentricities and at predictable locations, and eye tracking was used to ensure that subjects did not make eye movements during trials. These factors may have increased the probability of encoding more items in visual working memory.

The ideal observer analysis also generated a novel prediction that was subsequently verified in two experiments. Specifically, information theory predicts that the precision with which information can be stored in memory will vary as a function of the distribution of the information source in the external environment. In particular, signals with low variance are fundamentally easier to encode than signals with high variance. In keeping with this prediction, it was demonstrated that the accuracy of memory decreased as the variance of the information source increased. A simple information-theoretic model was able to parsimoniously account for this finding without any additional assumptions or mechanisms. To account for these same results, non-information-theoretic models would need to postulate an additional mechanism.

Although the present analysis is the first to quantitatively predict the effects of feature variance on performance, our empirical results are not unique. A recent study (Brady, Konkle, & Alvarez, 2009) has demonstrated that people have the ability to ‘compress’ visual information in memory, and hence store more information, when redundancies are introduced in the stimuli. Brady and Alvarez (2011) have demonstrated that ensemble statistics, such as the mean size of task-relevant features in a display, influence the storage of items in visual working memory. Other experiments have demonstrated that there is a similarity advantage in visual working memory (Lin & Luck, 2009; Mate & Baqués, 2009; Sanocki & Sulman, 2011), such that performance and capacity estimates tend to be higher when stimuli are homogeneous or low variance. Interestingly, Lin and Luck (2009) found that the advantage for low variance stimuli held regardless of whether feature variance remained constant for a block of trials or instead changed from trial to trial in unpredictable fashion. This suggests that subjects may be able to adapt memory representations based on the statistics of features on a single trial.

An interesting result from the experiments was that the estimated mean capacity was similar for line length and orientation. It is tempting to speculate that such a result implies that memory storage for length and orientation draw on the same central capacity store. This would predict that in a task where participants must encode orientation and length simultaneously, performance should be worse compared to the case of storing a single feature. This hypothesis has been challenged by several experimental studies that have shown no evidence for degradation in performance when multiple features are stored (Luck & Vogel, 1997; Vogel et al., 2001; Zhang & Luck, 2008). However, completely independent storage of distinct features may not be supported when the precision of memory representations is taken into account (Fougnie, Asplund, & Marois, 2010).

Adaptation and optimality in visual working memory

One assumption of the ideal observer analysis is that humans have access to accurate estimates of the uncertainty of their sensory systems and the variance of features in the task environment. In applying the ideal observer models to the human data, we discarded the initial trials from each experimental session. In theory, subjects may have observed enough evidence at this point to form relatively accurate estimates of the mean and variance of visual features. However, the possibility remains that subjects inaccurately estimated these statistics. In order for VWM to be an optimal system, the coding scheme used to encode signals must be optimal with respect to the statistics of the source. This is not a feature unique to our analysis of VWM, but rather a general result from information theory (Shannon & Weaver, 1949): efficient codes for information are fundamentally dependent upon the context in which that information occurs. If experimental subjects adopt inaccurate estimates of the signal variance, then the true capacity of VWM would be higher than the estimates obtained based on the observed data, with the implication that subjects used this larger capacity in a suboptimal manner.

In the neuroscience literature, there is significant interest in identifying the adaptability of neural codes to the statistics of an information source (Fairhall, Lewen, Bialek, & Steveninck, 2001; Dean, Harper, & McAlpine, 2005; David, Vinje, & Gallant, 2004). Dean et al. (2005) examined the case of adaptation of neural codes in the mammalian auditory system to changes in auditory stimulus intensity—a particularly interesting case as perceptible differences in sound intensity can vary over 12 orders of magnitude. They found that individual neurons were able to adapt their mean firing rate to improve coding accuracy in response to changes in a variety stimulus statistics, including changes to the variance of the stimuli. Importantly, such adaptation was observed to occur at the level of individual neurons extremely rapidly, on the order of seconds. This suggests at least the possibility that human subjects would be able to optimally adapt their encoded memory representations to the statistics of the information source. This possibility is also bolstered by recent computational simulations (Geisler, Najemnik, & Ing, 2009) that have characterized the optimal neural encoding scheme for natural visual features. The optimal stimulus encoders derived using this approach were found to be similar, at first approximation, to receptive fields found in primary visual cortex. Investigating whether optimal neural encoding extends to visual working memory represents an important topic for future research.

In tasks that place a minimum-precision requirement on memory, an endogenously controlled limit on the number of encoded items may reflect an optimal strategy for completing the task. The ideal observer framework does not preclude the possibility that the allocation of capacity among items is adaptive, for example, by adjusting the encoding process to optimize performance in each individual task. Zhang and Luck (2011) have recently tested this possibility in several experiments that manipulated the precision demands on visual working memory, but found that regardless of task demands, there was no empirical evidence for shifts in the number, or precision, of encoded memory representations. In contrast, subjects did exhibit shifting performance with different task demands when evaluated on iconic memory (a more immediate form of visual memory), as opposed to visual working memory performance. Based on these results, in conjunction with our own, it appears that while memory representations may be sensitive to the statistical regularities of an environment, the encoding process itself (the selection of items to be stored) may not be under complete endogenous control, or may possess only limited adaptability to changing task demands.

Potential applications of the framework

Although we have explored several different models of how memory capacity is divided among multiple items in a scene, there remain numerous other possibilities that warrant further investigation. One assumption common among the best-fitting models is that capacity is evenly divided between encoded items. Alternatively, there may be variance not just in the number of encoded items, but also in terms of how that capacity is divided, such that some items receive a greater share than others (Van den Berg et al., 2012). One possibility is that when different objects in a scene have different complexities, that more complex objects will receive a greater proportion of the available capacity. In at least one experimental test of this hypothesis (Barton, Ester, & Awh, 2009), it was found that the precision of memory representations appears to be independent of the complexity of other objects in a scene, suggesting that capacity may be allocated evenly among items, regardless of their complexity. We do not claim that the best-fitting models reported here capture all details of visual working memory in complete fidelity. Rather, the ideal observer approach has allowed the specification of models that improve over existing accounts, while rendering salient the relationships among existing models and allowing for their principled evaluation. It is our hope that the theoretical approach developed in this paper will also be useful in guiding the development of new experimental paradigms and tests of models that are better suited for discriminating among competing explanations.

Finally, another important aspect of human visual memory that was not addressed is the role of time (or more directly, forgetting) in governing performance. The present experiments used a fixed retention interval, and therefore cannot address the issue of decay or interference in visual working memory. Other experiments have more directly examined the role of time in visual memory. Eng and colleagues (Eng, Chen, & Jiang, 2005) found significant decrements in performance with retention intervals lasting 2 seconds. Zhang and Luck (2009) examined not only the effect of retention intervals lasting up to 10 seconds, but also how performance degraded over time. Using a cued-recall paradigm, they argue that memory representations do not gradually decay, but rather are terminated abruptly. Such an abrupt offset could be incorporated in the present modeling framework by assuming that encoded representations are disrupted at a rate given by a specified hazard function. An interesting question that may potentially be addressed using the ideal observer framework is whether the memory representations for stimulus items of different complexity may be disrupted at different rates, or to greater extents.

In summary, the combined empirical and modeling results presented here suggest that the most productive approach to understanding the nature of capacity limits in visual working memory may lie in treating memory as a communication channel that has been optimized, through evolution and development, towards the efficient coding and storage of visual information. This same approach of treating behavior as rationally or optimally adapted to a task environment has been widely influential in understanding other aspects of vision (Knill & Richards, 1996; Geisler, 2011) and higher-level cognition (J. R. Anderson, 1990). The results obtained in the present experiments are largely consistent with such an optimal memory system. Future research may uncover properties of visual working memory that fail to conform to the basic predictions of the ideal observer framework. However, by starting with an ideal model of performance as a basic assumption, an important reference has been provided to which future experimental results and models can be compared.

Appendix

Table A1.

Posterior mean estimates of parameters common across information-theoretic models. 95% highest density credible intervals for the sample mean are given in brackets below each parameter.

Experiment and parameter	Model
	Slots + averaging	Continuous resource	Binomial allocation	Flexible allocation
Orientation experiment
Lapse (low var.)	0.04 [0.033, 0.046]	0.054 [0.047, 0.061]	0.03 [0.024, 0.034]	0.035 [0.028, 0.041]
Lapse (high var.)	0.074 [0.063, 0.084]	0.11 [0.10, 0.12]	0.06 [0.047, 0.071]	0.071 [0.059, 0.084]
Bias	−0.59 [−0.81, −0.36]	−0.59 [−0.79, −0.38]	−0.72 [−0.95, −0.49]	−0.71 [−0.94, −0.48]
Sensory noise	4.62 [4.3, 4.93]	4.90 [4.57, 5.22]	4.3 [3.94, 4.63]	4.46 [4.11, 4.80]
Total capacity (bits)	4.16 [3.63, 4.91]	3.91 [3.75, 4.08]	4.62 [4.05, 5.39]	4.47 [3.97, 5.10]
Prob. matching exponent	2.0 [1.44, 2.83]		3.3 [2.8, 3.86]	3.60 [2.94, 4.36]
Item limit	3.87 [3.57, 4.21]
Line length experiment
Lapse (low var.)	0.10 [0.87, 0.11]	0.11 [0.096, 0.12]	0.065 [0.052, 0.078]	0.075 [0.061, 0.089]
Lapse (high var.)	0.13 [0.11, 0.14]	0.18 [0.16, 0.19]	0.11 [0.098, 0.13]	0.12 [0.11, 0.14]
Bias	0.033 [0.03, 0.37]	0.027 [0.025, 0.03]	0.034 [0.003, 0.038]	0.045 [0.041, 0.049]
Sensory noise	0.088 [0.083, 0.093]	0.094 [0.089, 0.99]	0.074 [0.068, 0.081]	0.080 [0.074, 0.086]
Total capacity (bits)	4.94 [3.81, 6.29]	4.06 [3.66, 4.52]	4.21 [3.43, 5.23]	4.57 [3.60, 5.71]
Prob. matching exponent	1.20 [0.66, 1.93]		0.93 [0.78, 1.1]	1.03 [0.84, 1.25]
Item limit	4.22 [3.78, 4.64]