Table 1. Optimal segmentation for synthetic data.

Network property	Type	k	Segments
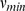
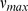
relative density	G	5	[1]–[4],[5]–[8],[9]–[12],[13]–[21],[22]–[36]	0.05	6.00
degree	L	5	[1]–[4], [5]–[8], [9]–[12], [13], [24], [25]–[36]	1.50	11.13
closeness	LG	4	[1]–[4], [5]–[15], [16]–[20], [21]–[36]	0.05	4.47
betweenness	LG	7	[1]–[4], [5]–[8], [9]–[12], [13]–[17], [18]–[21], [22]–[29], [30]–[36]	1.06	12.10
Existing method		k	Segments
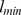
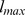
Ramakrishnan et al. [15]		5	[1]–[7], [8]–[12], [13]–[21], [22]–[29], [30]–[36]	4	9

The upper part of the table shows the result of the optimal segmentation for synthetic data based on dynamic programming, while the lower part contains the result based on the method of Ramakrishnan et al. [15]. In the upper table, the first and second columns show the name and the type of network properties used to determine the distances: G stands for global, L for local, and LG for local-global. The third column includes the number 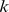of segments that maximize the objective 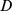with the dynamic programming approach. The resulting segments are given in the forth column, while the fifth and sixth columns contain the corresponding values of lower (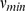) and upper (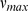) bound of the tuning parameter . 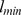The lower part also includes minimum and maximum length of the segments, i.e., and 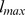, as parameters of the contending method.