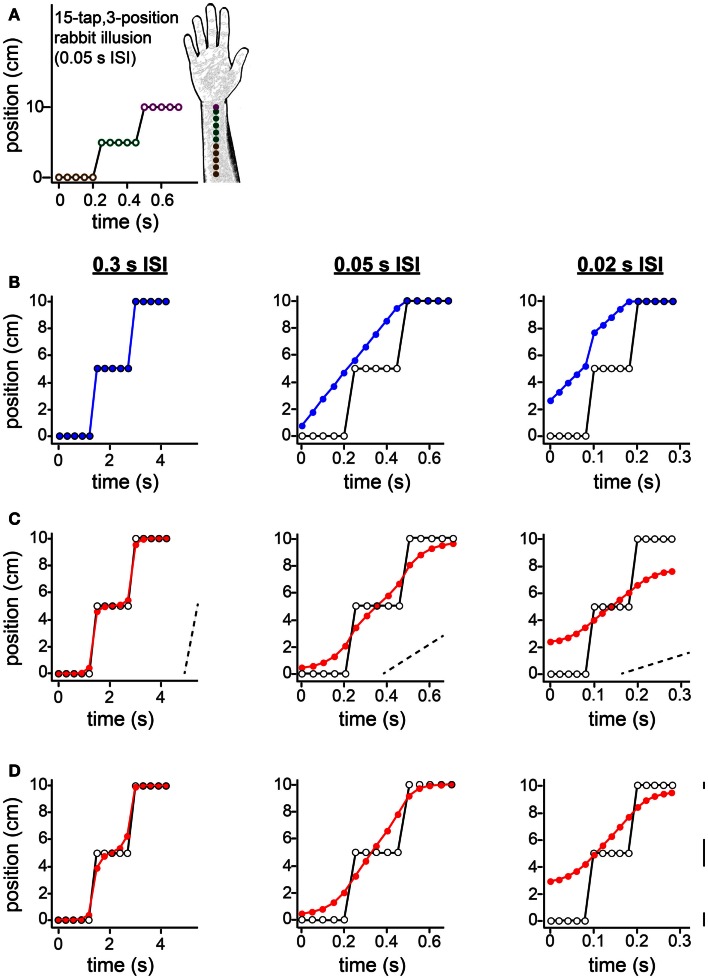
Figure 11.

The 15-tap rabbit illusion. (A) Geldard (1982) delivered five taps at each of three locations along the arm. When ISI between successive taps was 0.05 s, participants reported perceiving a linear spatial progression of taps 1 through 10 (forearm sketch). (B) The same spatial sequence shown in (A), at three different ISIs, resulted in distinct percepts (Geldard, 1982). Left: at 0.3 s ISI, perception was veridical. Center: at 0.05 s ISI, perception was as shown in (A). Right: at 0.02 s ISI, the taps were perceived to begin at a position between 2 and 3 cm along the arm, and to advance in a non-linear spatial progression. Open circles: true tap positions; blue points: human perceptual report. (C) The Bayesian low-speed observer’s perception with a standard setting of τ = 0.10 s (e.g., σ_s = 1 cm, σ_v = 10 cm/s) shows much similarity to participants’ subjective reports. Open circles: true tap positions; red points: Bayesian observer’s perception (mode of the posterior). Dashed slanted lines have slope 10 cm/s (i.e., 1σ_v). Note that the two rapid jumps in the true trajectory (from tap 5 to tap 6, and from tap 10 to tap 11) occur at a speed much greater than σ_v when the ISI is 0.05 s (center) or 0.02 s (right); thus, perceptual length contraction occurs in these cases. In contrast, at an ISI of 0.3 s (left), the trajectory does not strongly violate the observer’s low-speed expectation; thus, perception is nearly veridical. (D) The Bayesian low-speed observer’s perception can be made even closer to human reports if the value of σ_s varies along the arm. The observer’s percept at each ISI is shown for σ_s = 1, 2, and 0.5 cm around the proximal, middle, and distal arm regions, respectively. Line segments at right have length equal to 1σ_s at each location. The value of σ_v was fixed at 10 cm/s.