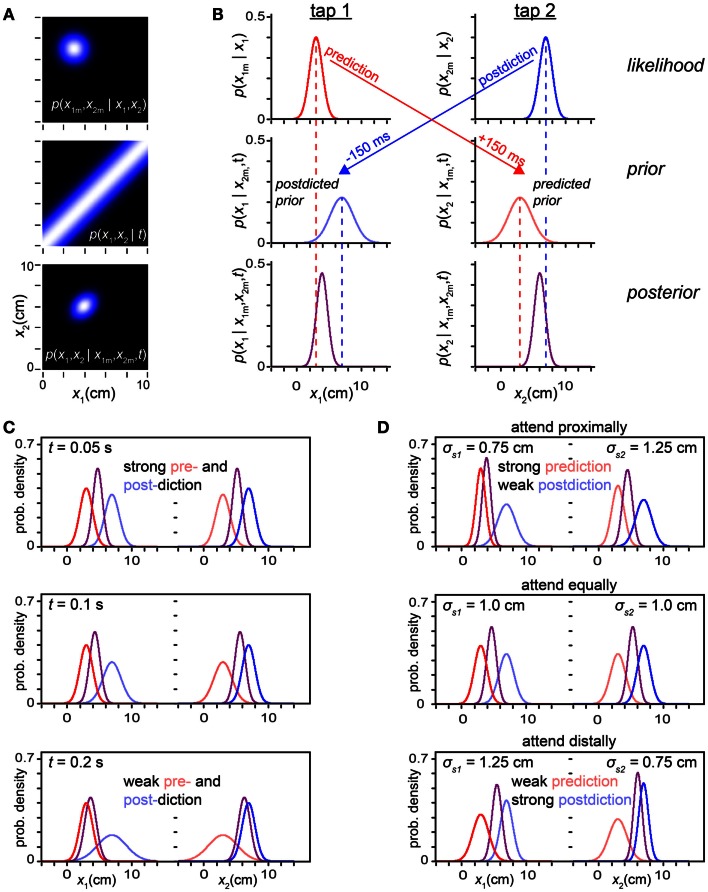
Figure 9.

Prediction-postdiction formulation. (A) The observer’s two-dimensional joint (x₁, x₂) likelihood function, prior and posterior densities. The measured trajectory was x_1m = 3 cm, x_2m = 7 cm, with t = 0.15 s. The observer settings were σ_s = 1 cm, σ_v = 10 cm/s. (B) The inference process in (A) reformulated as a series of one-dimensional inferences regarding x₁ and x₂ individually. Top left: the tap 1 likelihood function (red), p(x_1m | x₁), is centered on x_1m. Because of its low-speed expectation, the observer predicts (red arrow) that the most probable position for a future tap 2 will also be 3 cm. Middle right: the observer’s predicted prior over tap 2 (light red) represents its belief concerning the position of tap 2, projected 150 ms forward in time from the occurrence of tap 1. Top right: the observer’s tap 2 likelihood function (blue), p(x_2m | x₂), is centered on x_2m. Because of its low-speed expectation, the observer postdicts (blue arrow) that the most probable position for the preceding tap 1 was also 7 cm. Middle left: the observer’s postdicted prior over tap 1 (light blue) represents its belief concerning the position of tap 1, projected 150 ms backward in time from the occurrence of tap 2. Left column: using Bayes’ theorem, the observer multiplies the tap 1 likelihood function (red) by the tap 1 postdicted prior (light blue) to obtain the tap 1 posterior (purple). Right column: similarly, the observer multiplies the tap 2 likelihood function (blue) by the tap 2 predicted prior (light red) to obtain the tap 2 posterior (purple). (C) Individual tap likelihoods, priors, and posteriors graphed with the same color scheme as in (B), for three trajectories of progressively increasing ISI. At t = 0.05 s, pre- and postdiction both result in relatively sharp priors that exert a strong influence over the percept (mode of the posterior). As t is increased, the pre- and postdicted priors become lower and broader: pre- and postdiction become increasingly uncertain with the passage of time. The priors thus exert diminishing influence, and the percept approaches the measurement (compare to Figure 3A). For all panels in (C), σ_s = 1 cm, σ_v = 10 cm/s. (D) Effect of directed spatial attention, as in Figure 8. Top: a reduction in σ_s1 sharpens the tap 1 likelihood function, increasing the strength of prediction (note sharp predicted prior over tap 2), while an increase in σ_s2 broadens the tap 2 likelihood function, decreasing the strength of postdiction (note broad postdicted prior over tap 1). Middle: when σ_s1 = σ_s2, pre- and postdiction have equal strength. Bottom: reduction in σ_s2 relative to σ_s1 results in effects opposite those seen in the top panel. For all panels in (D), t = 0.06 s, σ_v = 10 cm/s.