Table 1.

Estimates of the parameters used in our dynamic HIV-FGS model

Variable	Meaning	Mean (95% CI)	BGR diagnostic upper CI limit*
	Probability of acquiring FGS, given childhood infection	0.457 (0.335–0.708)	1.193
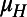	Duration of HIV/AIDS infection	8.533 (7.725–9.106)	1.077
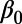	Intrinsic HIV transmission rate	0.317 (0.285–0.355)	1.079
	Relative increase HIV transmission from men	1.112 (1.004–1.388)	1.025
	Reduction rate of HIV transmission	5.096 (3.316–7.093)	1.131
	Scale of influence of deaths on HIV transmission	1.413 (1.172–1.648)	1.105
	Probability of acquiring FGS as a result of adulthood infection	0.017 (0.006–0.027)	1.183
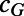	Enhance HIV transmission in FGS-infected women	1.758 (1.142–2.404)	1.130

These parameter estimates produced the best fit of our dynamic model to epidemiological data for HIV and FGS prevalence and coinfection among rural Zimbabwean women (2, 6). The dynamic model was fit to these data using a Bayesian MCMC method to allow calculation of distributions for possible values for each of these parameters. The means of these distributions and their associated 95% credible intervals (CIs) are shown.

^*Brooks–Gelman–Rubin (BGR) method monitors convergence of iterative simulations. If the upper limit of the credible interval of the BGR diagnostic statistic for a given parameter is <1.2, that parameter is considered to have converged to a robust solution (35).