Summary
Longitudinal studies often feature incomplete response and covariate data. Likelihood-based methods such as the expectation–maximization algorithm give consistent estimators for model parameters when data are missing at random (MAR) provided that the response model and the missing covariate model are correctly specified; however, we do not need to specify the missing data mechanism. An alternative method is the weighted estimating equation, which gives consistent estimators if the missing data and response models are correctly specified; however, we do not need to specify the distribution of the covariates that have missing values. In this article, we develop a doubly robust estimation method for longitudinal data with missing response and missing covariate when data are MAR. This method is appealing in that it can provide consistent estimators if either the missing data model or the missing covariate model is correctly specified. Simulation studies demonstrate that this method performs well in a variety of situations.
Keywords: Doubly robust, Estimating equation, Missing at random, Missing covariate, Missing response
1. Introduction
Incomplete longitudinal data often arise in comparative studies because of difficulties in ascertaining responses at scheduled assessment times, partially completed forms or questionnaires, patients’ refusal to undergo complete examinations, or study subjects failing to attend a scheduled clinic visit. For example, in the Alzheimer’s disease (AD) study introduced in Section 5, at each clinic visit, a patient may have an incomplete response (clinical diagnosis of AD) because the patient failed to attend the clinic, or the patient refused to undergo a complete examination; furthermore, the patient may have other information (covariates) missing because, for example, the patient did not finish the questionnaires or forms completely. Analyses based only on individuals with complete data can lead to invalid inferences if the mechanism leading to the missing data is dependent on the response. Under a missing completely at random (MCAR) mechanism (Little and Rubin, 2002), analyses based on generalized estimating equations (GEE; Liang and Zeger, 1986) yield consistent estimators of the regression parameters. However, when data are missing at random (MAR) or missing not at random (MNAR; Little and Rubin, 2002), analyses based on GEE generally give inconsistent estimators. Robins, Rotnitzky, and Zhao (1995) developed a class of inverse probability weighted generalized estimating equations (IPWGEE), which can yield consistent estimators when data are MAR. The weights are obtained from models for the missing data process, and these models must be correctly specified for the resulting estimators to be consistent. Alternatively, one can use the maximum likelihood method to estimate the parameters, and it gives a consistent estimator if the model is correctly specified, and the parameters are identified.
The literature on methods for missing data has primarily addressed either missing response or missing covariate data (see, e.g., Zhao, Lipsitz, and Lew, 1996; Horton and Laird, 1998; Lipsitz, Ibrahim, and Zhao, 1999; Fitzmaurice et al., 2001; Ibrahim, Lipsitz, and Horton, 2001). In practice, of course, data are often unavailable for both responses and covariates. In this situation, multiple imputation has been used under some parametric model assumptions (e.g., Schafer, 1997; Little and Rubin, 2002; van Buuren, 2007); Chen et al. (2008) provide a careful investigation of likelihood methods for missing response and covariate data via the EM algorithm; Shardell and Miller (2008) propose a marginal modeling approach to estimate the association between a time-dependent covariate and an outcome in longitudinal studies with missing response and missing covariate, but they focus on methods with an assumption that responses are independent; and Chen, Yi, and Cook (2010) develop a marginal method for a general working correlation matrix with missing response and missing covariates.
For the IPWGEE, to obtain a consistent estimator we need to correctly model the missing data process and also need to correctly model the response process given the covariates, but we do not need to specify the distribution of the missing covariates. If the missing data process model is misspecified, it can give biased estimators. That means, the IPWGEE method is sensitive to the misspecification of the missing data model but robust to the misspecification of the covariate process model. For the maximum likelihood method, we do not need to specify the missing data model when data are MAR, but we must correctly specify the joint distribution of the response and the covariates that have missing values. If the distribution of the covariates is misspecified, the maximum likelihood can give inconsistent estimators. That is to say, the maximum likelihood method is sensitive to the misspecification of the covariate model but robust to the misspecification of the missing data model when data are MAR.
A hybrid approach is the doubly robust estimator introduced by Lipsitz et al. (1999), in which they only considered cross-sectional studies with a missing covariate. This is an estimating equation approach with properties similar to the maximum likelihood. To obtain a consistent estimator of the regression parameters, either the missing data model or the distribution of the missing data given the observed data must be correctly specified, which is arguably more robust to the IPWGEE and the maximum likelihood method. The literature for the doubly robust estimator for the cross-sectional study includes Lunceford and Davidian (2004); Carpenter, Kenward, and Vansteelandt (2006); Davidian, Tsiatis, and Leon (2005); and Kang and Schafer (2007), etc. For longitudinal data, Van der Laan and Robins (2003) gave a general theory for the doubly robust estimator with monotone incomplete response; Bang and Robins (2005) showed how to perform doubly robust inference on longitudinal data with dropout; Seaman and Copas (2009) developed a doubly robust estimating equation on longitudinal data with dropout; the other literature includes Robins and Rotnitzky (2001) and Scharfstein, Rotnitzky, and Robins (1999). This literature, however, focuses primarily on monotone missing data patterns; Vansteelandt, Rotnitzky, and Robins (2007) developed regression models for the mean of repeated outcomes under nonignorable nonmonotone nonresponse, but they focus on the problem of missing response when conducting inference about the marginal mean and the conditional mean given the baseline observed covariates. Little work has been devoted to the longitudinal studies with both missing response and missing covariates. This is a challenge because, in most cases, the missingness patterns are not monotone, and the literature methods cannot be implemented. Furthermore, because of the incomplete covariates, the general weighted estimating equations do not work (as we show in Section 3.1), and new estimating equations need to be developed. In this article, we develop a new estimating equation method for binary longitudinal data with both missing response and missing covariates. This approach is appealing in that it can not only deal with the missing response and missing covariate problem with an intermittently missing data pattern but also yields the doubly robust and optimal efficient estimator.
The remainder of this article is organized as follows. In Section 2, we introduce notation and models. In Section 3, we give the forms of the estimating equations and provide details on estimation and inference. Simulation studies are given in Section 4. Data arising from an AD are analyzed in the application in Section 5. Concluding remarks are made in Section 6.
2. Notation and Models
2.1 Response Process
Suppose that n individuals are to be observed, with Ji repeated measurements for subject i, i = 1, …, n. Let Yi = (Yi1, Yi2, …, YiJi)T denote the Ji × 1 binary response vector for subject i that may be missing at some time points. Let Xi = (Xi1, Xi2, …, X iJi)T be the covariate vector that may be missing and be the covariate vector that is always observed, where Zij is the covariate vector for subject i at time j.
Define μij = E (Yij | Xi, Zi) = P(Yij = 1 | Xi, Zi), and let μi = (μi1, μi2, …, μiJi)T. Provided that the mean structure of Yij depends on the covariate vector for subject i at time j (Pepe and Anderson, 1994; Robins, Greenland, and Hu, 1999), we may consider the models for the mean of the form
for j = 1, …, Ji, i = 1, …, n, where g(·) is a known monotone link function, and is a vector of regression parameters. Here we suppose only one covariate Xij is potentially missing. Comments on how to deal with the problem when multiple covariates may be missing are given in the discussion. The variance for the response Yij is specified as vij = Var (Yij | Xi, Zi) = μij (1 − μij), which depends on the regression parameter vector β.
Let be the Kth-order correlation among components Yij1, Yij2, …, YijK of Yi, and ρ denote all the correlation parameters. For given subject i, the joint probability for a response vector Yi can be expressed via the Bahadur representation (Bahadur, 1961), which is given by
| (1) |
where yi is a realization of Yi, and is a realization of . This joint density requires modeling the correlation structures of all orders. In practice, it is often the case that the second order dominates the association structure while the third- and higher-order association is null or nearly null. Under such a circumstance, then the joint density is given by
| (2) |
In the following, we assume that the third- and higher-order association for Yi is null, and let Ci (ρ) denote the correlation matrix of Yi.
2.2 Missing Data Process
To indicate the availability of data we let Rij = 0 if Yij and Xij are missing, Rij = 1 if Yij is missing and Xij is observed, Rij = 2 if Yij is observed and Xij is missing, and Rij = 3 if Yij and Xij are observed. Let Ri = (Ri1, Ri2, …, RiJi)T, and R̄i j = {Ri1, …, Ri, j −1}.
Instead of modeling the joint probability P (Ri = ri | Yi, Xi, Zi) for Ri directly, because we are focusing on the longitudinal setting we restrict attention to conditional models of the form P (Ri j = ri j | R̄i j, Yi, Xi, Zi), which reflect the dynamic nature of the observation process over time; we can then obtain P (Ri = ri | Yi, Xi, Zi) through . Let λi j k = P (Ri j = k | R̄i j, Yi, Xi, Zi) denote the conditional probability, where k = 0, 1, 2, 3. We write these probabilities as conditional on the previous missing data indicators for the response and covariate, as well as the full vector of responses and covariates. The formulation thus far encompasses MCAR, MAR, and MNAR mechanisms because we have written the missing data model at assessment j as depending on the full vector of responses Yi and covariates Xi. For MAR mechanisms we require
| (3) |
where and represent the observed components of Yi and Xi, respectively. However, in the longitudinal setting with our conditional formulation it is very natural to make the further assumption that
| (4) |
for each time point j, where and denote the history of observed responses and covariates until time j − 1. It can be seen that (4) implies (3), but not vice versa. Moreover, while mechanism (3) covers a larger class of MAR models than (4), models under (4) are easier to formulate and interpret. Finally, many useful models can be embedded into the class characterized by (4), and this approach has been commonly used to model missing data processes with a MAR mechanism (e.g., Robins et al., 1995; Chen et al., 2010). For intermittently MAR data, it is often convenient to adopt the further assumption that the missing data indicators at time j depend only on the previously observed outcomes and covariates.
To model λijk, we use the generalized logistic link, with λij0 as a reference:
| (5) |
where uijk may be a subset of {R̄i j, , Zi}. Let .
It is noted that (5) may include too many parameters, which may increase the likelihood of misspecification. This makes the proposed method more appealing because we have a greater chance of obtaining accurate inference if the covariate model is modeled appropriately although the missing data model is misspecified. However, empirical study demonstrates that using appropriate model selection procedure can obtain a suitable model for the missing data mechanism (Ibrahim et al., 2005), thus reducing the likelihood of misspecification of the missing data model. As suggested by Ibrahim et al. (2005), one can use a step-up approach in constructing the missing data model by initially including only the main effects, then adding additional terms sequentially. One can then use the likelihood ratio or Akaike information criterion to evaluate the fit of each model. In many cases, the main effects model will be an adequate approximation to the missing data mechanism. One must be very careful to not build too large a model for the missing data mechanism because the model can easily become nonidentifiable.
Let πij = P (Rij = 3 | Yi, Xi, Zi) be the marginal probability of observing both Y and X at time j, given the entire vectors of responses and covariates; it is given by
This marginal probability can be expressed in terms of the marginal (conditional) probabilities, λijk’s.
2.3 Missing Covariate Model
Because subjects can have Xi missing, we must consider the density of Xi in some situations to obtain valid analysis, where we assume the joint density of Xi depends on the observed response and covariate Zi. In practice, this joint density can be expressed as
| (6) |
where X̄i j = {Xi1, …, Xi, j −1} is the history of the covariate Xij until time j − 1, and γ is the corresponding coefficient vector. It is noted that we made an assumption that .
3. Methods of Estimation
We denote the vector of all the parameters as θ = (βT, γT, αT)T. Our main interest is in estimation of β, with γ and α viewed as nuisance parameters.
3.1 Weighted Estimating Equation for the Response Parameters
Following the spirit of the IPWGEE approach of Robins et al. (1995), we introduce a weight matrix into the usual GEE to adjust for the effects of incomplete responses and covariates. That is, if we let , then the product yields an adjusted contribution from subject i, which involves the observed data alone. Moreover, this element has expectation zero, and hence unbiased estimating equations for β can be obtained as
| (7) |
where with being a p × Ji derivative matrix, and Vi the working covariance matrix for the response Yi.
In practice, the covariance matrix Vi is often expressed as , where Ci is a working correlation matrix, and Fi = diag (vij, j = 1, …, Ji), which is assumed to only depend on the marginal mean μi. When the working correlation matrix Ci is the identity matrix, (7) is computable. However, when a working independence assumption is not adopted, (7) may not be computable because elements of associated with the observed pairs (Yij, Xij) may be unknown because they involve other missing covariates Xi j′ (j′ ≠ j). Here we modify (7) to incorporate general working correlation matrices.
We define Δi = [δi j j′]Ji × Ji, j = 1, …, Ji, where δi j j′ = {I (Rij = 1, Ri j′ = 3) + I (Ri j = 3, Ri j′ = 3)}/πi j j′ for j ≠ j′, δijj = I (Rij = 3)/πij, and πi j j′ = P (Ri j = 1, Ri j′ = 3 | Yi, Xi, Zi) + P (Ri j = 3, Ri j′ = 3 | Yi, Xi, Zi). Let , where A • B = [aij · bij] denotes the Hadamard product of Ji × Ji matrices A = [aij] and B = [bij]. By introducing the weight matrix Δi (α), we ensure that all required elements of Mi can be computed.
The generalized estimating functions for β are given by
| (8) |
where Ui (β, α) = Di Mi (Yi − μi). It is easy to see that estimating function (8) depends on the observed data and the parameters only, and hence is computable.
For the estimating equations (8), to obtain a consistent estimator, we need to correctly specify the missing data model. If the missing data model is misspecified, it can yield biased estimators. Under a MAR mechanism, Robins et al. (1995), Scharfstein et al. (1999), and Van der Laan and Robins (2003) proposed methods to improve the robustness of the inverse probability weighted estimators. The idea is to modify these inverse weighted equations by adding an appended function in the a tangent space of the conditional distribution of Ri, yielding an augmented estimating function that remains unbiased. With suitable choice of the appended function, we can get the doubly robust estimators. This approach has, to our knowledge, only been investigated to address the missingness with either incomplete response or covariate processes, but not both. Now, we describe ways for the double robustness for the general missingness patterns when either the covariates model or missing data model is correctly specified.
Following the same spirit of Van der Laan and Robins (2003), the general form of the augmented estimating functions for the general missingness patterns can be written as
| (9) |
where φi is a function in the tangent space of the conditional distribution of Ri with mean zero. The optimal φi,opt is chosen as the projection of Ui onto the tangent space of the conditional distribution of Ri. It is not hard to show that, in Hilbert space,
with
![]() , where
, where
 is a vector a 1’s with length Ji, and
and
denote the missing part of Yi and Xi, respectively. We can then solve estimating equations,
is a vector a 1’s with length Ji, and
and
denote the missing part of Yi and Xi, respectively. We can then solve estimating equations,
to obtain the estimator of β. It can be shown that the resulting estimator for β is robust to the misspecification of either the missing data model or the covariates model. The proof is given in the Appendix.
As commented by a referee, if Y and X are partially observed, and we assume an independence working correlation matrix, observations with Y unobserved contribute nothing to the estimation. However, when we allow correlations then we do need the individuals with Y missing but X observed for the correlation terms. Further, if we assume independence, then estimation is much simpler: the iterative process in Section 3.3 is not needed. Thus a simple way to analyze the data is to use doubly robust independence equations, and then an appropriate (i.e., sandwich) standard error. However, this estimator may not be efficient, which is demonstrated in Section 4 (see Table 3) if the true correlation matrix is not independent.
Table 3.
Empirical bias, standard deviation, and coverage probabilities for the proposed approaches to estimation and inference with incomplete covariate and response data with independence working correlation matrix (γ1 = 2 and α2 = −2 : missing proportion is about 40%)
|
β0
|
β1
|
β2
|
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Method | Bias% | SD | CP% | Bias% | SD | CP% | Bias% | SD | CP% |
| ρ = 0.6 | |||||||||
| DREE(x+, r+) | 2.1 | 0.138 | 94.7 | 0.1 | 0.133 | 95.1 | −1.0 | 0.131 | 94.5 |
| DREE(x+, r−) | 1.6 | 0.146 | 94.4 | 1.7 | 0.134 | 94.3 | −1.4 | 0.110 | 94.9 |
| DREE(x−, r+) | −1.4 | 0.114 | 94.6 | −1.0 | 0.099 | 95.0 | −0.9 | 0.094 | 94.8 |
| DREE(x−, r−) | −9.2 | 0.108 | 91.7 | −6.9 | 0.097 | 92.1 | −4.0 | 0.093 | 93.5 |
| ρ = 0.3 | |||||||||
| DREE(x+, r+) | 0.9 | 0.105 | 94.8 | 1.0 | 0.103 | 95.2 | 0.1 | 0.083 | 95.0 |
| DREE(x+, r−) | −0.4 | 0.119 | 94.7 | 0.1 | 0.114 | 94.9 | 0.1 | 0.091 | 95.3 |
| DREE(x−, r+) | −1.5 | 0.100 | 94.4 | −1.7 | 0.095 | 94.4 | −0.8 | 0.085 | 94.6 |
| DREE(x−, r−) | −7.4 | 0.096 | 92.8 | −6.0 | 0.097 | 93.2 | 2.0 | 0.080 | 94.0 |
| ρ = 0 | |||||||||
| DREE(x+, r+) | 0.5 | 0.090 | 95.1 | 0.1 | 0.095 | 95.0 | −0.1 | 0.080 | 94.6 |
| DREE(x+, r−) | 0.2 | 0.089 | 95.2 | 0.4 | 0.099 | 94.6 | 1.0 | 0.081 | 94.4 |
| DREE(x−, r+) | 1.0 | 0.087 | 94.9 | 0.2 | 0.096 | 95.2 | 0.1 | 0.078 | 94.9 |
| DREE(x−, r−) | 0.8 | 0.090 | 94.5 | 0.2 | 0.097 | 94.7 | −0.4 | 0.080 | 94.5 |
In practice, the parameters γ and α are unknown, and one must replace γ and α with a consistent estimator. We describe how to obtain an estimator in the next subsection.
3.2 Estimation for the Nuisance Parameters
Because we are assuming that the covariate is MAR, we can obtain the estimator of γ through maximizing the observed likelihood function
which is equivalent to solve the estimating equation , where .
For the estimation of the missing data parameter α, we can also use maximum likelihood estimator. Note that the log likelihood for α is given by
and the score function is
Solving the estimating equation S3(α) = 0 leads to the maximum likelihood estimator α̂.
3.3 Estimation and Inferences
In this section, we give details on the estimation and inference for the parameter β. Plugging in the estimated parameters γ̂ and α̂, we then solve the following estimating equations for the parameter β:
| (10) |
For simplicity, we use notation S1(β) and S1i (β) to denote S1(β, γ̂, α̂) and S1i (β, γ̂, α̂) in the following. It can be shown that, provided that the response model, p(yi | xi, zi), is correctly specified, either the correct specification of the missing data model, p(ri | xi, yi, zi), or the correct specification of the covariate model, , leads to the asymptotically unbiased estimator of β. The details of proof are given in the Appendix.
To solve estimating equations (10), we employ an expectation–maximization (EM)-type algorithm (Lipsitz et al., 1999). The key is that we need to calculate the conditional expectation in S1.
When X is discrete, then the second part in S1i can be written as
where
can be regarded as a weight. The distribution of P (Yi = yi | Xi = xi, Zi) and can be obtained from (2) and (6), respectively.
We now introduce the EM-type algorithm to solve S1(β̂) = 0 as follows:
Obtain an initial value of the parameter β = β(0);
At the tth step, we have β(t), and calculate ;
- Treating as fixed, solve for β(t+1), where
(11) Iterate until convergence to, say β̂, which gives the solution to S1(β̂) = 0.
When X is continuous, (11) becomes
| (12) |
where the weights
To solve (12), we need the integrations. In this case, rather than use numerical integration, we would suggest using rejection sampling (Gilks and Wild, 1992). Adopting this approach we would sample ( ) from the conditional density . Repeat this L times, with the lth draw of ( ) denoted by ( ). Then
We can similarly introduce an iterative algorithm as is done when X is discrete.
To state the asymptotic properties of β̂, we define , and .
Theorem 1
Suppose that the regularity conditions stated in the Appendix hold, if either the missing data model or the covariate model is correctly specified, we have
where β0 is the true value of β, γ0 and α0 are the probability limits of γ̂ and α̂, and . The proof is given in the Appendix. To make inferences, we consistently estimate the matrix Γ by , and Σ by , where θ̂ = (β̂T, γ̂T, α̂T)T, , and .
We note that the preceding development treats the working correlation matrix Ci as known. In applications, Ci may contain an unknown parameter vector, say ρ, that is functionally independent of the β, γ, and α parameters but must be estimated. Following the spirit of Liang and Zeger (1986), we suggest an iterative fitting procedure by which the current values of β̂ and α̂ are used to compute a weighted moment-type estimator obtained as a function of the weighted Pearson residual , where δij = I (Rij = 3)/πij. The expression for the estimator of ρ depends on the correlation structure. For example, for an unstructured correlation matrix where Corr(Yij, Yi j′) = ρj j′ for j ≠ j′, ρj j′ is estimated by . Here is calculated in the same way as πij is calculated above. It is easy to show that ρ̂j j′ is an unbiased estimator.
To obtain a n1/2-consistent estimator in Theorem 1, we require that the probability πij is bounded away from 0. In practice, if s are relatively too small for some subjects, the inverse probability weights will inflate the effects of these subjects and lead to great biases. Thus, an investigator should examine the weight distribution carefully before implementing the proposed method. Some protection using truncation or downgrading may be an option for controlling weights properly, if unreasonable influences are detected (Bang, 2005).
4. Numerical Studies
4.1 Performance of the Proposed Estimators
In this subsection, we evaluate the performance of the proposed method compared to other methods commonly used in practice through simulation studies. In the simulation studies, we focus on a setting where Ji = J = 3 and n = 500. We simulate the longitudinal binary responses from a model with
| (13) |
where Zij is a time-varying binary covariate generated from Bin(1, 0.5), and Xij is a time-varying binary covariate, which may be missing at some time points and is generated from the model
| (14) |
where ωi j = P(Xi j = 1 | X̄i j, Zi j). We take β0 = log (1.5), β1 = log(0.5), β2 = log(2), γ0 = log(1), γ2 = 2, and let γ1 vary from −2 to 2. The correlation matrix of the response vector Yi is exchangeable with correlation coefficient ρ.
For the missing data process, we take
| (15) |
for k = 1, 2, 3, where y†i,j −1 = yi,j −1 if yi,j −1 is observed and 0 otherwise, x†i,j −1 = xi,j −1 if xi,j −1 is observed and 0 otherwise. The true values are taken as α0k = log (1.5), α1k1 = log (1.5), α1k2 = log (1.3), α1k3 = log (1.1), α3k = −2, and α2k = α2, varying from −2 to 2.
In the simulations, we always assume that the model for (Yi | xi, zi), equation (13), is correctly specified. We consider the following 10 methods: (1) The proposed method, i.e., the douldy robust estimating equation (DREE) method that both the missing data model (15) and covariate model (14) are correctly specified, which we denote DREE(x+, r+). (2) The proposed method that the missing data model is correctly specified, but the model for ω is misspecified as
| (16) |
which we denote DREE(x−, r+). (3) The proposed method that the model for ω is correctly specified, but the missing data model is misspecified as
| (17) |
which we denote DREE(x+, r−). (4) The proposed method that the model for ω is misspecified as (16), and the missing data model is misspecified as (17), which we denote DREE(x−, r−). (5) The maximum likelihood method via the EM algorithm with the covariate model incorrectly specified as (16), which we denote EM(x−). (6) The simple weighted GEE (not the robust method) method with the missing data model incorrectly specified as (17), which we denote GEE(r−). (7) The complete case (CC) analysis using the GEE method, which we denote cc. (8) The augmented weighted GEE analysis based on Chen et al. (2010) with correct missing data model (denoted as AIP(r+)), which solves the following estimating equation:
where Ai (α) is a function of the observed data that is free of β with expectation 0, and η is the regression coefficient of Ai in the population regression of Ui regress Ai and S3i. Here we choose Ai, in the same spirit of Chen et al. (2010), as , where
, and . (9) The simple weighted GEE (not the robust method) method with the missing data model correctly specified, which we denote GEE(r+). (10) The maximum likelihood method via the EM algorithm to the subgroup with either no missing data or Y observed and X missing, and the covariate model is correctly specified, which we denote EM *(x+). In each setting, we perform 2000 simulations.
The results are reported in Table 1, where the bias is the percentage relative bias, SD is the standard deviation for the 2000 simulations, and CP represents the empirical coverage probability for 95% confidence intervals. It is seen that the DREE(x−, r−), EM(x−), EM*(x+), GEE(r−), and cc approaches yield larger biases and poor coverage probabilities; as the response correlation coefficient increases, the performance becomes worse. The DREE(x+, r+), DREE(x+, r−), DREE(x−, r+), GEE(r+), and AIP(r+) methods provide ignorable finite sample biases and good coverage probabilities. The DREE(x+, r+), DREE(x+, r−), and DREE(x−, r+) estimators are more efficient than the AIP(r+) estimator, and the AIP(r+) estimator is more efficient than the GEE(r+) estimator. To clarify for readers the effect of the missing data model, we report the expected missing value patterns in Table 2 when ρ = 0.3, γ1 = 2, and α2 = −2.
Table 1.
Empirical bias, standard deviation, and coverage probabilities for ten approaches to estimation and inference with incomplete covariate and response data (γ1 = 2 and α2 = −2 : missing proportion is about 40%)
|
β0
|
β1
|
β2
|
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Method | Bias% | SD | CP% | Bias% | SD | CP% | Bias% | SD | CP% |
| ρ = 0.6 | |||||||||
| DREE(x+, r+) | 1.1 | 0.103 | 94.5 | 1.0 | 0.093 | 94.6 | −0.8 | 0.086 | 94.7 |
| DREE(x+, r−) | 1.2 | 0.107 | 94.6 | 1.8 | 0.102 | 94.7 | −1.1 | 0.094 | 94.7 |
| DREE(x−, r+) | −1.3 | 0.105 | 94.5 | −1.2 | 0.098 | 94.9 | −1.4 | 0.088 | 94.6 |
| GEE(r+) | 1.3 | 0.119 | 94.3 | 1.5 | 0.110 | 94.4 | −0.6 | 0.106 | 94.6 |
| AIP(r+) | 2.1 | 0.111 | 94.6 | 1.2 | 0.104 | 94.3 | −1.5 | 0.101 | 94.3 |
| DREE(x−, r−) | −9.5 | 0.108 | 91.4 | −7.3 | 0.099 | 91.9 | −4.3 | 0.096 | 94.2 |
| EM(x−) | −25.0 | 0.140 | 90.5 | −73.3 | 0.136 | 80.6 | 26.3 | 0.110 | 88.3 |
| EM*(x+) | 12.1 | 0.142 | 90.4 | −10.6 | 0.146 | 92.0 | −0.1 | 0.139 | 95.2 |
| GEE(r−) | 32.0 | 0.230 | 81.3 | 18.8 | 0.251 | 80.4 | 2.6 | 0.264 | 94.2 |
| cc | −272.6 | 0.690 | 89.0 | 72.6 | 0.977 | 96.0 | 28.8 | 0.655 | 95.2 |
| ρ = 0.3 | |||||||||
| DREE(x+, r+) | 1.4 | 0.095 | 95.2 | 0.9 | 0.091 | 94.8 | 0.1 | 0.081 | 94.7 |
| DREE(x+, r−) | 0.8 | 0.109 | 94.6 | 1.0 | 0.101 | 94.7 | 0.6 | 0.083 | 94.8 |
| DREE(x−, r+) | −0.6 | 0.097 | 94.7 | −0.9 | 0.092 | 94.4 | −0.3 | 0.082 | 94.5 |
| GEE(r+) | 1.0 | 0.116 | 94.4 | 0.5 | 0.114 | 94.4 | −1.3 | 0.093 | 94.5 |
| AIP(r+) | 2.3 | 0.111 | 94.2 | 1.9 | 0.109 | 94.3 | −2.2 | 0.089 | 94.3 |
| DREE(x−, r−) | −7.5 | 0.097 | 93.8 | −6.3 | 0.095 | 94.1 | 0.0 | 0.083 | 95.2 |
| EM(x−) | −10.2 | 0.121 | 91.7 | −86.1 | 0.122 | 74.3 | 21.6 | 0.099 | 90.8 |
| EM*(x+) | 6.6 | 0.126 | 95.4 | −4.4 | 0.145 | 95.0 | −0.3 | 0.139 | 95.8 |
| GEE(r−) | 15.9 | 0.215 | 81.4 | 11.5 | 0.252 | 86.4 | −1.3 | 0.255 | 94.5 |
| cc | −221.1 | 0.955 | 75.8 | −26.8 | 1.112 | 97.0 | −27.7 | 1.423 | 93.9 |
| ρ = 0 | |||||||||
| DREE(x+, r+) | 0.1 | 0.089 | 94.8 | 0.2 | 0.098 | 94.5 | 0.1 | 0.079 | 94.6 |
| DREE(x+, r−) | −0.4 | 0.089 | 94.4 | 0.9 | 0.099 | 94.7 | 0.9 | 0.080 | 94.8 |
| DREE(x−, r+) | −0.3 | 0.089 | 94.6 | −0.2 | 0.098 | 94.2 | −0.4 | 0.080 | 94.9 |
| GEE(r+) | 0.2 | 0.100 | 95.2 | 1.2 | 0.101 | 95.3 | 0.8 | 0.089 | 95.2 |
| AIP(r+) | 0.5 | 0.097 | 94.4 | 0.8 | 0.099 | 94.5 | 1.4 | 0.086 | 94.5 |
| DREE(x−, r−) | −0.0 | 0.089 | 94.7 | −0.6 | 0.097 | 94.8 | −0.1 | 0.081 | 94.5 |
| EM(x−) | 49.1 | 0.102 | 84.9 | −109.0 | 0.106 | 71.5 | −12.0 | 0.079 | 93.5 |
| EM*(x+) | 2.5 | 0.125 | 96.4 | 0.2 | 0.145 | 95.2 | −1.2 | 0.138 | 93.2 |
| GEE(r−) | 3.8 | 0.225 | 95.2 | 3.2 | 0.259 | 94.3 | 2.8 | 0.259 | 94.2 |
| cc | −157.7 | 0.828 | 85.7 | −6.8 | 1.021 | 93.3 | −19.0 | 1.356 | 94.5 |
Table 2.
Missing value patterns when ρ = 0.3, γ1 = 2, and α2 = −2 : “+” and “−” represent observed and missing values, respectively
| Y1 | X1 | Y2 | X2 | Y3 | X3 | n (%) |
|---|---|---|---|---|---|---|
| + | + | + | + | + | + | 1.0 |
| + | + | + | + | + | − | 0.8 |
| + | + | + | + | − | + | 0.9 |
| + | + | + | + | − | − | 7.4 |
| + | + | + | − | + | + | 1.9 |
| + | + | + | − | + | − | 1.8 |
| + | + | + | − | − | + | 1.8 |
| + | + | + | − | − | − | 4.7 |
| + | + | − | + | + | + | 1.4 |
| + | + | − | + | + | − | 1.4 |
| + | + | − | + | − | + | 1.3 |
| + | + | − | + | − | − | 6.1 |
| + | + | − | − | + | + | 17.3 |
| + | + | − | − | + | − | 17.6 |
| + | + | − | − | − | + | 17.3 |
| + | + | − | − | − | − | 17.5 |
To study the performance of the proposed method with misspecified working correlation matrix, we consider using the independence working correlation matrix. Table 3 lists the results. As expected, the DREE(x−, r−) still yields larger biases when the true correlation coefficient ρ is not equal to 0; DREE(x+, r+), DREE(x+, r−), and DREE(x−, r+) give negligible biases; however, using the independence working correlation matrix yields less efficient estimators than the estimators with correct specification of the correlation matrix when ρ ≠ 0; there is, however, not much difference in the efficiency between the two types of estimators when ρ = 0, which makes sense.
4.2 Impact of Model Misspecification
The validity of the proposed method depends on correct specification of the model for the response process and either the missing data process or the covariate process. Here we investigate the impact of misspecification of the missing data process model and/or the covariate process model.
Let θ̂† denote the estimator for θ when the missing data process and the covariate process models are misspecified. To characterize the asymptotic bias of θ̂†, we use the methods of White (1982) to find the value to which θ̂† converges. In the spirit of Rotnitzky and Wypij (1994); Fitzmaurice, Molenberghs, and Lipsitz (1995); and Cook, Zeng, and Yi (2004), we take the expectation of Si (θ) with respect to the true distribution of G = (Ri, Yi, Xi, Zi) and set it equal to zero. The solution to this equation, denoted θ†, is the value to which θ̂† converges in probability. If G is the sample space for G, and P(g; θ) is the true probability of observing the realized value g of G, then solving the equation,
| (18) |
gives the relationship between θ and θ†, and enables one to characterize the asymptotic bias.
In this study, response measurements are featured by the same model (13) with ρ = 0.3; the true model for missing data indicators is (15), and the true model for the missing covariate model is (14).
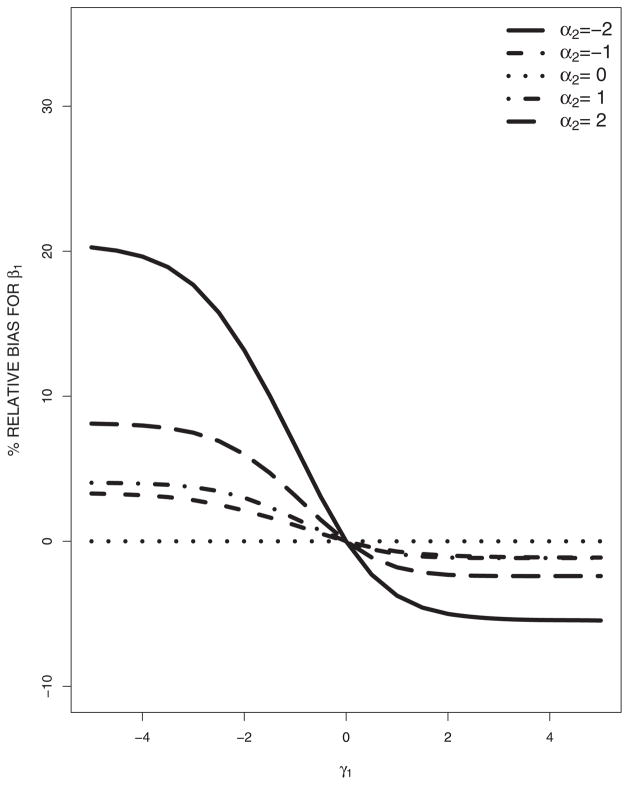
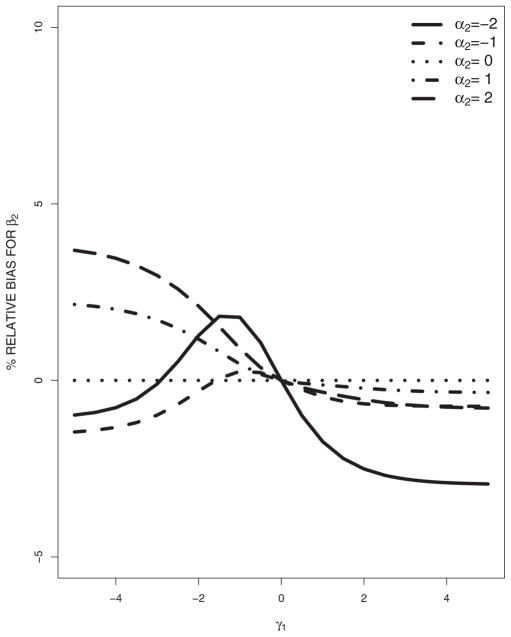
Now we consider the misspecification of the missing data model and the covariate model. The misspecified models are (16) and (17). Figures 1 and 2 plot the asymptotic percentage relative biases of β1 and β2 against γ1 as α2 changes. It is seen that β1 and β2 are sensitive to the misspecification of the missing data and covariate models. As the absolute value of α2 goes to 0, the relative biases decrease; as the absolute value of γ1 goes to 0, the relative biases decrease. For fixed α2 that are not very big, the relative biases are flat functions of γ1, and the biases are small, indicating that the estimator is less sensitive to the misspecification of the covariate model in our model set-up; while for fixed γ1 that are not very close to 0, the relative biases change rapidly as α2 changes, indicating that the estimator is more sensitive to the misspecification of the missing data model in our model set-up; however, this may not be generally true.
Figure 1.
Asymptotic percentage relative bias of β1 with misspecified covariate model and missing data model.
Figure 2.
Asymptotic percentage relative bias of β2 with misspecified covariate model and missing data model.
In summary, estimation of the response parameters is generally sensitive to the misspecification of the missing data model and/or covariate model, although the degree of the sensitivity could be varying for different kinds of misspecifications.
5. Application to an Alzheimer’s Disease Study
We apply the proposed method to the National Alzheimer’s Coordinating Center Uniform Data Set. One of the goals of the study is to investigate the risk factors that influence the occurrence of AD. The response we are using is the clinical diagnosis for subjects as having AD (Yes/No), because the gold standard for AD is through neuropathological examination, which is not available for the majority of subjects. The covariates that may influence the occurrence of AD include sex, congestive heart failure (CVCHF, yes/no), family history of dementia (FHDEM, yes/no), diabetes (DIABETE, yes/no), depression or dysphoria (DEP., yes/no), hypertension (HYPERT, yes/no), education (EDUC, years), Mini-Mental State Exam (MMSE) score, and age, in which CVCHF, diabetes, DEP., hypertension, and MMSE are time varying, and the others are not. There are 16,223 subjects from 29 AD Centers included at the entry of this study. Follow-up visits for subjects are scheduled at approximately 1-year intervals, with up to four clinical visits until 2008. The median follow-up is 2. However, patients may miss a clinic visit or refuse to undergo a clinical examination during the clinic visit, leading to the incomplete responses; furthermore, patients may partially complete a form or questionnaire that the DEP. covariate is based on, leading to incomplete covariates. We think the MAR mechanism may be reasonable because, for example, a patient’s visit to a clinic may depend on his/her previous observed diagnosis of disease status: if s/he was diagnosed AD last year, s/he may be likely to attend the clinic visit this year to control the disease efficiently. There are 8724 subjects with complete data observed. About 11.9% of observation time points have the response and DEP. missing simultaneously; about 31.2% of observation time points have the responses missing and the DEP. observed; about 3.2% of observation time points have the behavioral assessment missing but the response observed; and about 53.7% of observation time points have both the response and the DEP. observed.
Consider the following regression model for the response process logit
| (19) |
where uij is the covariate vector at time point j, which includes the function of sex, CVCHF, FHDEM, diabetes, DEP., hypertension, education, MMSE, age, and the indicator variables for centers.
For the missing indicators, we build the following regression models:
| (20) |
where vijk include functions of history of the missing indicators, sex, CVCHF, FHDEM, diabetes, hypertension, education, MMSE, age, previous observed response, and previous observed depression status.
For the covariate, we build the following model:
| (21) |
where ωij is the conditional probability that patient i at time j is depressed given the covariate vector wij, which may include functions of history of depression, sex, CVCHF, FHDEM, diabetes, hypertension, education, MMSE, age, and previous observed response.
Here we use four methods to analyze the data. The first method, labeled “EM,” is the maximum likelihood method via the EM algorithm; the second method, labeled “DREE,” is the proposed doubly robust method based on the augmented estimating equations; the third method is the CC analysis via the GEE; the fourth method, labeled “RE,” is the random effects (intercept) model by using the available data. The results are reported in Table 4, where the parameters are (adjusted) log odds ratios (except the intercept term) of diagnosis of AD at time j. The response model we use is (19) with unstructured correlation matrix, and the missing data and covariate models are (20) and (21), respectively. Here we only list the effects for the risk factors and omit the center effects though some of them are highly significant. All methods reveal the same results: sex, CVCHF, FHDEM, and EDUC have no significant effect on the occurrence of AD; depression has a negative effect on the occurrence of AD; MMSE has a positive effect to protect the occurrence of AD; diabetes and hypertension have positive effects to protect the occurrence of AD; and age has a negative effect on the occurrence of AD.
Table 4.
Log odds ratios (except the intercept term) of diagnosis of AD for the National Alzheimer’s Coordinating Center Uniform Dataset (the correlation matrix is unstructured for EM, DREE, and CC methods)
| EM
|
DREE
|
CC
|
RE
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | Est. | SE | p | Est. | SE | p | Est. | SE | p | Est. | SE | p |
| (Intercept) | −0.831 | 0.157 | <0.001 | −0.611 | 0.138 | <0.001 | −0.165 | 0.195 | 0.398 | −0.289 | 0.207 | 0.163 |
| SEX(F) | −0.056 | 0.031 | 0.075 | −0.041 | 0.028 | 0.141 | −0.031 | 0.039 | 0.430 | −0.049 | 0.034 | 0.150 |
| CVCHF | 0.128 | 0.075 | 0.087 | −0.045 | 0.070 | 0.524 | −0.062 | 0.097 | 0.521 | 0.068 | 0.084 | 0.418 |
| DEP. | 0.314 | 0.028 | <0.001 | 0.415 | 0.030 | <0.001 | 0.449 | 0.042 | <0.001 | 0.378 | 0.031 | <0.001 |
| MMSE | −0.003 | 0.001 | <0.001 | −0.005 | 0.001 | <0.001 | −0.024 | 0.001 | <0.001 | −0.019 | 0.001 | <0.001 |
| FHDEM | 0.009 | 0.035 | 0.788 | 0.023 | 0.030 | 0.459 | −0.026 | 0.043 | 0.548 | 0.014 | 0.038 | 0.702 |
| DIABETE | −0.139 | 0.045 | 0.002 | −0.253 | 0.041 | <0.001 | −0.163 | 0.057 | <0.005 | −0.172 | 0.049 | <0.001 |
| HYPERT | −0.223 | 0.033 | <0.001 | −0.236 | 0.029 | <0.001 | −0.217 | 0.041 | <0.001 | −0.224 | 0.035 | <0.001 |
| EDUC | 0.000 | 0.002 | 0.858 | 0.001 | 0.001 | 0.418 | 0.001 | 0.002 | 0.549 | 0.000 | 0.002 | 0.873 |
| AGE | 0.020 | 0.002 | <0.001 | 0.018 | 0.002 | <0.001 | 0.019 | 0.002 | <0.001 | 0.019 | 0.002 | <0.001 |
For the missing data model, we carry out standard diagnostic tests for the fit of regression models by comparing a model with an expanded model to do a model selection. Here, we only list the results for the final model without reporting the tables due to limited space. Significance of the previous missing indicator indicates that there exists strong series dependence; sex, CVCHF, MMSE, FHDEM, diabetes, hypertension, education, age, the previous observed response, and the previous observed depression status are also significant in some missing indicator models, indicating that the MCAR are not feasible. Therefore, we can draw the conclusion that the CC analysis can draw a wrong conclusion about a relationship between a risk factor and the occurrence of AD. Our doubly robust method may have a very good chance to reduce the biases of the estimate if the MAR assumption is true. Rejecting the MCAR may not be sufficient to say the missing data mechanism is MAR because it can be MNAR. For the MNAR mechanism, we comment on it in the next section.
6. Discussion
The consistent estimators of longitudinal data analysis with both missing response and missing covariates under MAR generally depend on the correct specification of the missing data model or the covariate model. Likelihood-based methods are robust to the misspecification of the missing data process model, while the weighted estimating equation method is robust to the misspecification of the covariate model. In this article, we develop a doubly robust estimation method, which is robust to the misspecification of either the missing data model or the covariate model, but not both. Simulation studies have shown that, subject to the correct specification of the response model, the estimators are consistent and empirical studies have shown that there is negligible bias in finite samples, when the missing data or the covariate model is correctly specified.
The asymptotic studies have provided insight into the nature of the biases one can expect with different types of model misspecification, which suggests that there is a very good chance that our proposed method will reduce the bias with which the covariate model is misspecified and the missing data model is approximately correct. Use of model diagnostics for the missing data process, perhaps most easily carried out in the MAR setting through model expansion, is warranted. It appears that empirically there is often little price to pay for introducing additional covariates into the missing data regression models. This is comforting because the more comprehensive the missing data model the more plausible it is since there is no residual dependence on the missing response, say.
The doubly robust methods can be unstable if weights are extreme and will be wrong if both models are misspecified. Furthermore, it can also draw the wrong conclusion if the data are not MAR. In many applications, however, data may not be sufficient to distinguish the MAR from MNAR mechanism. Actually, it is generally not possible to check formally for the presence of a MNAR mechanism, so sensitivity analysis is required if this is a serious concern. Scharfstein et al. (1999); Rotnitzky, Robins, and Scharfstein (1998); Scharfstein and Irizarry (2003); Robins, Rotnitzky, and Scharfstein (2000); and Robins and Rotnitzky (2001) each discuss strategies for conducting sensitivity analyses for marginal semiparametric methods for incomplete data. For other approaches, several authors have proposed the use of global and local influence tools to sensitivity analyses in missing data contexts (e.g., Kenward, 1998; Verbeke and Molenberghs, 2000; Molenberghs, Kenward, and Goetghebeur, 2001; Van Steen, Molenberghs, and Thjis, 2001; Verbeke et al., 2001; Zhu and Lee, 2001; Jansen et al., 2003; Molenberghs and Verbeke, 2005). Another route for sensitivity analysis is to consider pattern-mixture models as a complement to selection models. Other approaches have been considered by Copas and Li (1997), Copas and Shi (2000), and Copas and Eguchi (2001). More details on some of these procedures can be found in Molenberghs and Verbeke (2005), and Little and Rubin (2002).
We focused here primarily on estimation and inference regarding one covariate that is subject to missingness. Multiple covariates subject to missing are very common in practice. A future research is to extend this method to the multiple missing covariates problem. The idea is that we build missing data models to construct the weights in the weighted estimating equations, and we also need to build joint models for the covariates that are subject to missingness, which is challenging in practice, especially for missing covariates with both continuous and categorical.
Acknowledgments
The authors thank the associate editor and referees for their constructive comments and suggestions. This work was partially supported by grants from the National Natural Science Foundation of China (NSFC 30728019) and the National Institutes of Health (U01AG016976). Dr X-HZ, Ph.D., is presently a Core Investigator and Biostatistics Unit Director at the Northwest HSR&D Center of Excellence, Department of Veterans Affairs Medical Center, Seattle, WA. This article presents the findings and conclusions of the authors. It does not necessarily represent those of VA HSR&D Service.
Appendix: Proof of the Doubly Robust Estimation Property and Theorem 1
Proof of the doubly robust estimation property
Let , then using the first Taylor series expansion, it can be shown that
which implies that
| (A1) |
where I11, I12, and I13 are the appropriate submatrices of [−∂E{S(θ)}/∂θT ]−1.
-
Missing data model is correctly specified
Suppose the missing data model and p(yi | xi, zi) are correctly specified, but the distribution of (xi | zi, ) is misspecified. Then, in (10) we rewrite and as and because of the MAR assumption, where the subscript “*” represents the expectation taken over the wrongly specified distribution for ( ) and .
If the missing data model is correctly specified, we have E(δijk) = 1, and thus E(Δi) =
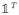 ,
, and E(Ni) = 0. Therefore, we have
, and
, if the distribution of (yi | xi, zi) is correctly specified. That means E{S1(θ)} = 0. It is easy to show that E{S3(α)} = 0.Now if the distribution of (xi | zi, ) is incorrectly specified, then E{S2(γ)} ≠ 0. However, the second term on the right-hand side of (A1) still has expectation 0. Using the theory of partitioned matrices, it can be shown that I12 = 0 if E{∂S1(θ)/∂γT } = 0. Note that the first term of S1(θ) does not depend on γ, so the derivative is equal to 0, hence
,
, and E(Ni) = 0. Therefore, we have
, and
, if the distribution of (yi | xi, zi) is correctly specified. That means E{S1(θ)} = 0. It is easy to show that E{S3(α)} = 0.Now if the distribution of (xi | zi, ) is incorrectly specified, then E{S2(γ)} ≠ 0. However, the second term on the right-hand side of (A1) still has expectation 0. Using the theory of partitioned matrices, it can be shown that I12 = 0 if E{∂S1(θ)/∂γT } = 0. Note that the first term of S1(θ) does not depend on γ, so the derivative is equal to 0, henceThus all the terms on the right-hand side of (A1) have expectation 0, and β̂ is asymptotically unbiased.
-
correctly specified
Suppose that the distribution of (yi | xi, zi), and (xi | zi, ) are correctly specified but the missing data indicator model is incorrectly specified. To be specific, suppose that πijk is misspecified as , and πij is misspecified as , which are still functions of xi, yi, and zi. We define Δi = [δ̃i j k ] with for k ≠ j and . We show that E{S1(θ)} = 0, E {S2(γ)} = 0 and I13 = 0, implying that each term on the right-hand side of (A1) has 0 expectation and β̂ is asymptotically unbiased. Note that expectation of the first term of S1i (θ) isIf both p(yi | xi, zi) and are correctly specified, then the joint probability is correctly specified, and hence the expectation of the second term of S1i (θ) is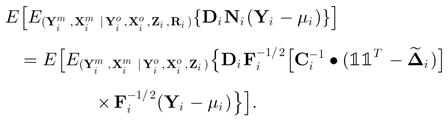 Thus we have
Thus we haveif the distribution of (yi | xi, zi) is correctly specified. Similarly, we can prove that E[S2i (γ)] = 0.
If the missing data model is misspecified, then E{S3(α)} ≠ 0. However, the third term on the right-hand side of (A1) still has expectation 0 if I13 = 0. By using the theory of partitioned matrices, we can show that I13 = 0 if E{δS1(θ)/∂αT} = 0. Note thatfor j = 1, …, p3, where p3 = dim(α). Then all the three terms on the right-hand side of (A1) have expectation 0, and β̂ is asymptotically unbiased if the distribution of (yi | xi, zi) and (xi | zi, ) are correctly specified.
Proof of Theorem 1
The regularity conditions required in Theorem 1 include standard conditions that are assumed for the estimating function theory, plus the requirement for the missing data processes and covariate process. Specifically, we require P (Ri j = 3 | R̄ij, Yi, Xi, Zi) is bounded away from zero. This condition ensures that the estimating functions in (8) are bounded, which is necessary for a -consistent estimator. Other routine conditions are similar to those in Robins et al. (1995) with a proper modification.
By standard Taylor expansion arguments we have that
| (A2) |
and
| (A3) |
Furthermore, based on the proof of the doubly robust properties, we have E[S1i (β0, γ0, α0)] = 0 if either the missing data model or the covariate model is correctly specified. Thus, another Taylor expansion gives
Replacing (A2) and (A3) into (A4), we obtain
If Γ(β0, γ0, α0) is nonsingular, we have
Then the asymptotic distribution of n1/2(β̂ − β0) follows by Slutsky’s theorem and the central limit theorem.
References
- Bahadur RR. A representation of the joint distribution of responses to n dichotomous items Studies in Item Analysis and Prediction. In: Solomon H, editor. Stanford Mathematical Studies in the Social Sciences VI. Stanford, California: Stanford University Press; 1961. pp. 158–168. [Google Scholar]
- Bang H. Medical cost analysis: Application to colorectal cancer data from the SEER medicare database. Contemporary Clinical Trials. 2005;26:586–597. doi: 10.1016/j.cct.2005.05.004. [DOI] [PubMed] [Google Scholar]
- Bang H, Robins JM. Doubly robust estimation in missing data and causal inference models. Biometrics. 2005;61:962–972. doi: 10.1111/j.1541-0420.2005.00377.x. [DOI] [PubMed] [Google Scholar]
- Carpenter J, Kenward M, Vansteelandt S. A comparison of multiple imputation and inverse probability weighting for analyses with missing data. Journal of the Royal Statistical Society, Series A. 2006;169:571–584. [Google Scholar]
- Chen B, Yi GY, Cook RJ. Weighted generalized estimating functions for incomplete longitudinal response and covariate data that are missing at random. Journal of the American Statistical Association. 2010;105:336–353. [Google Scholar]
- Chen Q, Ibrahim JG, Chen M, Senchaudhuri P. Theory and inference for regression models with missing responses and covariates. Journal of Multivariate Analysis. 2008;99:1302–1331. doi: 10.1016/j.jmva.2007.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cook RJ, Zeng L, Yi GY. Marginal analysis of incomplete longitudinal binary data: A cautionary note on LOCF imputation. Biometrics. 2004;60:820–828. doi: 10.1111/j.0006-341X.2004.00234.x. [DOI] [PubMed] [Google Scholar]
- Copas JB, Eguchi S. Local sensitivity approximations for selectivity bias. Journal of the Royal Statistical Society, Series B. 2001;63:871–895. [Google Scholar]
- Copas JB, Li HG. Inference for non-random samples (with discussion) Journal of the Royal Statistical Society, Series B. 1997;59:55–96. [Google Scholar]
- Copas JB, Shi JQ. Meta-analysis, funnel plots and sensitivity analysis. Biometrics. 2000;1:247–262. doi: 10.1093/biostatistics/1.3.247. [DOI] [PubMed] [Google Scholar]
- Davidian M, Tsiatis AA, Leon S. Semiparametric estimation of treatment effect in a pretest-posttest study without missing data. Statistical Science. 2005;20:261–301. doi: 10.1214/088342305000000151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fitzmaurice GM, Molenberghs G, Lipsitz SR. Regression models for longitudinal binary data responses with informative drop-outs. Journal of the Royal Statistical Society, Series B. 1995;57:691–704. [Google Scholar]
- Fitzmaurice GM, Lipsitz SR, Molenberghs G, Ibrahim JG. Bias in estimating association parameters for longitudinal binary responses with drop-outs. Biometrics. 2001;57:15–21. doi: 10.1111/j.0006-341x.2001.00015.x. [DOI] [PubMed] [Google Scholar]
- Gilks WR, Wild P. Adaptive rejection sampling for Gibbs sampling. Applied Statistics. 1992;41:337–348. [Google Scholar]
- Horton HJ, Laird NM. Maximum likelihood analysis of generalized linear models with missing covariates. Statistical Methods in Medical Research. 1998;8:37–50. doi: 10.1177/096228029900800104. [DOI] [PubMed] [Google Scholar]
- Ibrahim JG, Lipsitz SR, Horton N. Using auxiliary data for parameter estimation with nonignorable missing outcomes. Applied Statistics. 2001;50:361–373. [Google Scholar]
- Ibrahim JG, Chen MH, Lipsitz SR, Herring AH. Missing-data methods for generalized linear models. Journal of the American Statistical Association. 2005;100:332–346. [Google Scholar]
- Jansen I, Molenberghs G, Aerts M, Thijs H, Van Steen K. A local influence approach applied to binary data from a psychiatric study. Biometrics. 2003;59:409–418. doi: 10.1111/1541-0420.00048. [DOI] [PubMed] [Google Scholar]
- Kang JDY, Schafer JL. Demystifying double robustness: A comparison of alternative strategies for estimating a population mean from incomplete data. Statistical Science. 2007;22:523–539. doi: 10.1214/07-STS227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kenward MG. Selection models for repeated measurements with nonrandom dropout: An illustration of sensitivity. Statistics in Medicine. 1998;17:2723–2732. doi: 10.1002/(sici)1097-0258(19981215)17:23<2723::aid-sim38>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]
- Liang KY, Zeger SL. Longitudinal data analysis using gerneralized linear models. Biometrika. 1986;73:13–22. [Google Scholar]
- Lipsitz SR, Ibrahim JG, Zhao LP. A new weighted estimating equation for missing covariate data with properties similar to maximum likelihood. Journal of the American Statistical Association. 1999;94:1147–1160. [Google Scholar]
- Little RJA, Rubin DB. Statistical Analysis with Missing Data. 2. New York: John Wiley; 2002. [Google Scholar]
- Lunceford JK, Davidian M. Stratification and weighting via the propensity score in estimation of causal treatment effects: A comparative study. Statistics in Medicine. 2004;23:2937–2960. doi: 10.1002/sim.1903. [DOI] [PubMed] [Google Scholar]
- Molenberghs G, Verbeke G. Models for Discrete Longitudinal Data. New York: Springer; 2005. [Google Scholar]
- Molenberghs G, Kenward MG, Goetghebeur E. Sensitivity analysis for incomplete contingency tables. Applied Statistics. 2001;50:15–29. [Google Scholar]
- Pepe MS, Anderson GL. A cautionary note on inference for marginal regression models with longitudinal data and general correlated response data. Communications in Statatistcs, Simulation and Computation. 1994;23:939–951. [Google Scholar]
- Robins JM, Rotnitzky A. Comment on “Inference for semiparametric models: Some questions and answer,” by P. J. Bickel and J. Kwon. Statistical Sinica. 2001;11:920–936. [Google Scholar]
- Robins JM, Rotnitzky A, Zhao LP. Analysis of semi-parametric regression models for repeated outcomes in the presence of missing data. Journal of the American Statistical Association. 1995;90:106–121. [Google Scholar]
- Robins JM, Greenland S, Hu FC. Estimation of the causal effect of a time-varying exposure on the marginal mean of a repeated binary outcome (with discussion) Journal of the American Statistical Association. 1999;94:687–712. [Google Scholar]
- Robins JM, Rotnitzky A, Scharfstein DO. Sensitivity analysis for selection bias and unmeasured confounding in missing data and causal inference models. In: Halloran EM, Berry D, editors. Statistical Models in Epidemiology, the Enviroment, and Clinical Trials. New York: Springer-Verlag; 2000. p. 1.p. 94. [Google Scholar]
- Rotnitzky A, Wypij D. A note on the bias of the estimators with missing data. Biometrics. 1994;50:1163–1170. [PubMed] [Google Scholar]
- Rotnitzky A, Robins JM, Scharfstein DO. Semi-parametric regression for repeated outcomes with nonignorable nonresponse. Journal of the American Statistical Association. 1998;93:1321–1339. [Google Scholar]
- Schafer JL. Analysis of Incomplete Multivariate Data. New York: Chapman and Hall; 1997. [Google Scholar]
- Scharfstein DO, Irizarry RA. Generalized additive selection models for the analysis of studies with potentially nonignorable missing outcome data. Biometrics. 2003;59:601–613. doi: 10.1111/1541-0420.00070. [DOI] [PubMed] [Google Scholar]
- Scharfstein DO, Rotnitzky A, Robins JM. Adjusting for nonignorable drop-out using semiparametric nonresponse models (with discussion) Journal of the American Statistical Association. 1999;94:1096–1120. [Google Scholar]
- Seaman S, Copas A. Doubly robust generalized estimating equations for longitudinal data. Statistics in Medicine. 2009;28:937–955. doi: 10.1002/sim.3520. [DOI] [PubMed] [Google Scholar]
- Shardell M, Miller R. Weighted estimating equations for longitudinal studies with death and non-monotone missing time-dependent covariates and outcomes. Statistics in Medicine. 2008;27:1008–1025. doi: 10.1002/sim.2964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Buuren S. Multiple imputation of discrete and continuous data by fully conditional specification. Statistical Methods in Medical Research. 2007;16:219–242. doi: 10.1177/0962280206074463. [DOI] [PubMed] [Google Scholar]
- Van Der Laan MJ, Robins JM. Unified Methods for Censored Longitudinal Data and Causality. New York: Springer; 2003. [Google Scholar]
- Vansteelandt S, Rotnitzky A, Robins JM. Estimation of regression models for the mean of repeated outcomes under non-ignorable nonmonotone nonresponse. Biometrika. 2007;94:841–860. doi: 10.1093/biomet/asm070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Steen K, Molenberghs G, Thijs H. A local influence approach to sensitivity analysis of incomplete longitudinal ordinal data. Statistical Modelling: An International Journal. 2001;1:125–142. [Google Scholar]
- Verbeke G, Molenberghs G. Linear Mixed Models for Longitudinal Data. New York: Springer; 2000. [Google Scholar]
- Verbeke G, Molenberghs G, Thijs H, Lesaffre E, Kenward MG. Sensitivity analysis for non-random dropout: A local influence approach. Biometrics. 2001;57:43–50. doi: 10.1111/j.0006-341x.2001.00007.x. [DOI] [PubMed] [Google Scholar]
- White H. Maximum likelihood estimation under misspecified models. Econometrica. 1982;50:1–26. [Google Scholar]
- Zhao LP, Lipsitz SR, Lew D. Regression analysis with missing covariate data using estimating equations. Biometrics. 1996;52:1165–1182. [PubMed] [Google Scholar]
- Zhu HT, Lee SY. Local inference for incomplete data models. Journal of the Royal Statistical Society, Series B. 2001;63:111–126. [Google Scholar]