Fig. 1.

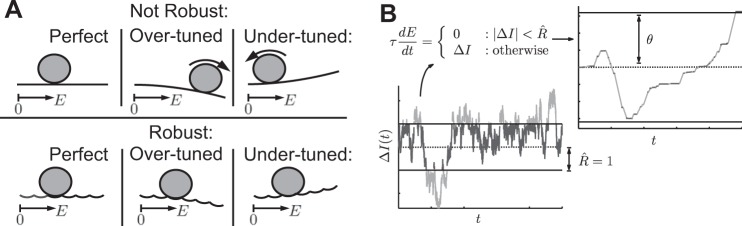
Schematic of neural integrator models. A: visualizing integration via an energy surface (Pouget and Latham 2002; Goldman et al. 2009). The robust integrator can “fixate” at a range of discrete values, indicated by a sequence of potential wells, despite mistuning of circuit feedback. These wells can be arbitrarily “close” in the energy landscape, providing a mechanism for graded persistent activity. Without these wells (the nonrobust case), activity in a mistuned integrator would either exponentially grow or decay, as at top. Perturbing the robust integrator from one well to the next, however, requires sufficiently strong momentary input. B: as a consequence, low-amplitude segments in the input signal ΔI(t), below a robustness limit R, are not accumulated by a robust integrator: only the high-amplitude segments are. The piecewise definition of Eq. 5 captures this robustness behavior, resulting in the accumulated activity shown, and may be related to, e.g., a detailed bistable-subpopulation model. A decision is expressed when the accumulated value E(t) crosses the decision threshold θ.