Rapid emission angle selection for rotating-shield brachytherapy

Abstract

Purpose: The authors present a rapid emission angle selection (REAS) method that enables the efficient selection of the azimuthal shield angle for rotating shield brachytherapy (RSBT). The REAS method produces a Pareto curve from which a potential RSBT user can select a treatment plan that balances the tradeoff between delivery time and tumor dose conformity.

Methods: Two cervical cancer patients were considered as test cases for the REAS method. The RSBT source considered was a Xoft Axxent^TM electronic brachytherapy source, partially shielded with 0.5 mm of tungsten, which traveled inside a tandem intrauterine applicator. Three anchor RSBT plans were generated for each case using dose-volume optimization, with azimuthal shield emission angles of 90°, 180°, and 270°. The REAS method converts the anchor plans to treatment plans for all possible emission angles by combining neighboring beamlets to form beamlets for larger emission angles. Treatment plans based on exhaustive dose-volume optimization (ERVO) and exhaustive surface optimization (ERSO) were also generated for both cases. Uniform dwell-time scaling was applied to all plans such that that high-risk clinical target volume D₉₀ was maximized without violating the D_2cc tolerances of the rectum, bladder, and sigmoid colon.

Results: By choosing three azimuthal emission angles out of 32 potential angles, the REAS method performs about 10 times faster than the ERVO method. By setting D₉₀ to 85–100 Gy₁₀, the delivery times used by REAS generated plans are 21.0% and 19.5% less than exhaustive surface optimized plans used by the two clinical cases. By setting the delivery time budget to 5–25 and 10–30 min/fx, respectively, for two the cases, the D₉₀ contributions for REAS are improved by 5.8% and 5.1% compared to the ERSO plans. The ranges used in this comparison were selected in order to keep both D₉₀ and the delivery time within acceptable limits.

Conclusions: The REAS method enables efficient RSBT treatment planning and delivery and provides treatment plans with comparable quality to those generated by exhaustive replanning with dose-volume optimization.

INTRODUCTION

The deliverable radiation dose using conventional brachytherapy (BT) is limited by organs at risk (OARs) located adjacent to or inside the tumor. In the case of cervical cancer treated with intracavitary BT, the rectum, bladder, and sigmoid colon limit the dose that can be delivered to the tumor.^{1, 2} This is an important clinical limitation since conventional single channel BT dose distributions for nonradially symmetric tumors are delivered with radiation sources that produce radially symmetric dose distributions about the applicator. For laterally extended tumors, achieving the desired tumor dose coverage using the intracavitary BT approach is challenging.^{3, 4}

Rotating shield brachytherapy (RSBT) was first described theoretically by Ebert as a means of improving brachytherapy dose distribution tumor conformity for single-catheter⁵ and multicatheter⁶ treatments. In both studies, Ebert modeled RSBT dose distributions from a partially shielded radiation source with the dosimetric characteristics of ¹⁹²Ir, but shielded with an unknown material that provided a sufficiently low transmission rate for RSBT to be effective. Although the ideal transmission for a RSBT shield is dependent on the clinical case and the emission angle, a shield transmission of 50% was shown to be unacceptable.⁵ An ¹⁹²Ir-based RSBT system for rectal cancer is currently under development,⁷ and the minimum tungsten alloy shield thickness reported for the system is 10 mm, which, combined with the applicator required for delivery, may make using the system for cervical cancer RSBT challenging.

The advent of high-dose-rate electronic brachytherapy (eBT) sources such as the 40–50 kVp eBT delivery system (Xoft Axxent^TM, Xoft Inc., Sunnyvale, CA) allows for small-diameter intracavitary RSBT applicators to be used for cervical cancer. The eBT device is a 2.25 mm diameter x-ray tube, contained in a 5.4 mm diameter water cooling catheter.⁸ The transmission rate can be finely controlled, making delivery of less than 0.1% transmission possible when using a 0.5 mm tungsten shield. The eBT device with the rotating shield and applicator combination provides a RSBT system with an overall diameter of less than 7 mm (half the cross-sectional area of a 10 mm diameter shield) as shown in Fig. 1a. Although there are no commercially available applicators with rotatable partial shields to the best knowledge of the authors, there is a conceptual patented design.⁹

Figure 1.

(a) A cross view of the conceptual model of a partially shielded eBT source in RSBT (drawn to scale). (b) A longitudinal section view of the beamlet arrangement.

Of the nearly 12 000 new cases of cervical cancer diagnosed annually in the U.S., about 57% (6800) (Ref. ¹⁰) are stage IB2 or higher. They are typically treated with a combination of cisplatin chemotherapy, external beam radiation therapy, and a brachytherapy boost to the tumor.¹¹ Cervical cancer brachytherapy has improved considerably in recent years through the use of magnetic resonance imaging (MRI)-guidance.^{1, 2} Tumor regions that would be underdosed using intracavitary brachytherapy alone can be better visualized on MRI scans and treated with supplementary needle-based interstitial brachytherapy improving outcomes.^{4, 12, 13, 14} In a 78-patient study of stage IB-IVA cervical cancer, patients with tumors of greater than 5 cm in size (40% of the patients) improved local tumor control and overall survival following additional needle-based interstitial brachytherapy.³ Increased local tumor control at 3 yr went from 64% to 82% (p = 0.09) and 3-yr overall survival increased from 28% to 58% (p = 0.003) relative to conventional intracavitary methods.³ As increasing the delivered tumor dose using supplementary interstitial BT has improved cervical cancer outcomes relative to intracavitary BT alone, it may be expected that RSBT based on eBT could be a less-invasive alternative to intracavitary plus interstitial BT, while still improving patient outcomes relative to intracavitary BT alone. RSBT for cervical cancer is considered in this study, although in principle RSBT may be delivered to breast,¹⁴ prostate,⁶ gynecological, and rectal¹⁵ cancers.

For a given radiation source, single-catheter RSBT treatment planning and delivery is more time-consuming than conventional single-catheter BT delivery for multiple reasons. First, the rotating shield blocks photons generated from the radiation source, increasing the amount of energy the source must emit during a treatment.⁵ Since each eBT source has a finite lifetime, efficient usage of each source is necessary in order for the therapy to be cost-effective. Second, the treatment planning process for RSBT is more time-consuming than that for conventional BT. This is because the number of optimization variables for RSBT are greater than that of conventional BT by a factor of K, where K is the number of allowed irradiation directions per dwell position. For example, Shi et al.¹⁶ reported multidirectional breast BT treatment planning and delivery times of 120 and 37 min, respectively, while conventional BT treatment planning and delivery times were both about 5 min. Since patients tend to be under general or spinal anesthesia during BT treatment planning and delivery, prolonging these processes is expensive and inefficient.

It is assumed that RSBT users will have access to multiple shields with a range of azimuthal emission angles. It is also assumed that a single azimuthal emission angle is used to deliver a patient's RSBT treatment. The optimal azimuthal emission angle for single-catheter, single-shield RSBT will be tumor-dependent, especially in the case of a target with an ellipsoidal cross section and a catheter that passes through the center of mass of the cross section. For a target with an ellipsoidal cross section with a width of three times the height, an azimuthal emission angle smaller than 180° will be necessary in order to treat the lateral tumor extensions without overdosing the normal tissue anterior and posterior to the tumor. For more cylindrical targets, as the width and height of the tumor approach each other, larger azimuthal emission angles become attractive, and the treatment times will decrease accordingly. In the case of a target with a cylindrical cross section, the ideal source is an unshielded one, and a conventional BT case is best.

The choice of an azimuthal emission angle is an important component in single-catheter, single-shield, RSBT planning. However, determining the ideal azimuthal emission angle for a given case is efficiently not an intuitive task. Using exhaustive replanning with dose-volume optimization (ERVO) is able to determine the ideal azimuthal emission angle, but the computational cost may not be acceptable and the treatment planning time would increase in proportion to the number of available shields; using exhaustive replanning with surface-homogeneity optimization (ERSO) as a heuristic can decrease the computational cost, but it may suffer the quality of the plan. In this work a rapid emission angle selection (REAS) method is presented that enables RSBT users to intuitively select an ideal balance between RSBT treatment time and dose distribution quality for a given clinical case.

MATERIALS AND METHODS

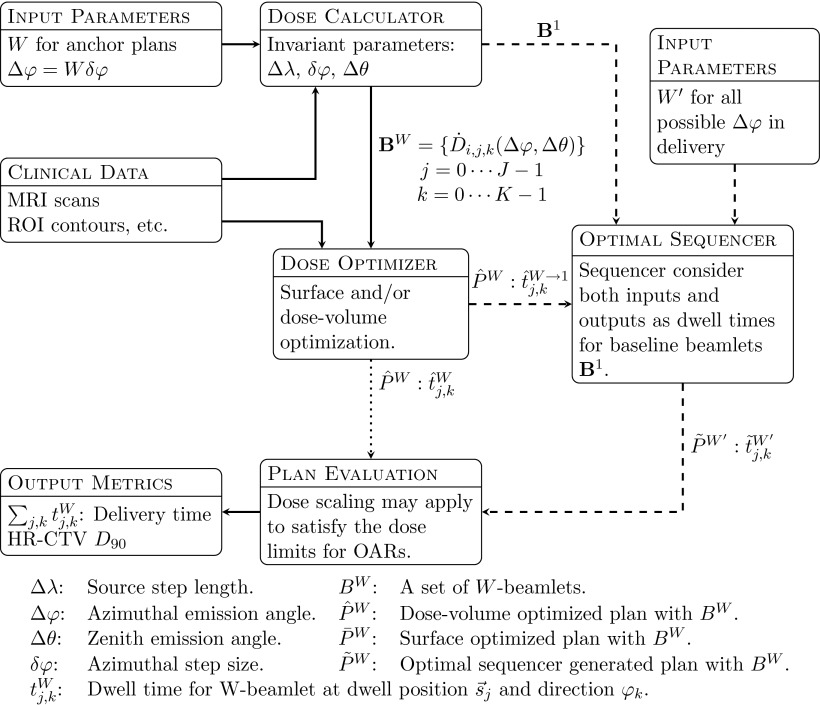
The key process in REAS is to separate the dose optimization stage into an anchor plan optimization stage and an optimal sequencing stage. In the anchor plan optimization stage, RSBT treatment plans are generated for azimuthal emission angles of 90°, 180°, or 270°. These plans are then converted into baseline equivalent plans by disassembling the beamlets used in the anchor plan optimization stage into a set of beamlets with a small azimuthal emission angle, which we will call the baseline beamlets. For any given azimuthal emission angle, we use the optimal sequencing stage to reassemble the baseline beamlets back into beamlets within the specified azimuthal emission angle. This decoupling process allows for the calculation of the dose optimization procedure independent of the azimuthal emission angle used for delivery. Optimal sequencing, the key part of REAS, requires only half minute of computational time for all 32 azimuthal emission angles used in this study except the one used for the anchor plan, as opposed to 20 min required to generate the baseline plans. A delivery efficiency curve is generated in about 1 min, enabling the user to select the treatment plan that balances dose distribution quality and delivery time.

Radiation source model and dose calculation

Define a RSBT beamlet, ${\dot{D}}_{i,j,k}\left(\Delta \phi ,\Delta \theta \right)$, as the dose rate at the point ${\stackrel{\rightharpoonup }{r}}_i$ due to a shielded radiation source at dwell position ${\stackrel{\rightharpoonup }{s}}_j$ ( j = 0, …, J − 1). The shield has an azimuthal emission angle of Δφ and a zenith emission angle of Δθ [see Fig. 1b]. The irradiation direction of the beamlet is defined by φ_k, which is the lower of the two azimuthal angles defining the aperture: φ_k = (k mod K) δφ (k = 0, …, K − 1), where δφ = 360°/K is the azimuthal step size between neighboring beamlets and K is set to 32 in this study. The mod operation denotes modular arithmetic, enabling beamlet referencing with arbitrary integer k-values such that φ_k+K+1 = φ_k+1. The upper azimuthal edge of beamlet k is located at angle φ_k + Δφ. The total dose delivered to point i from a shielded source with azimuthal and zenith emission angles of Δφ and Δθ, respectively, is calculated as a time-weighted sum of the appropriate beamlets over all dwell positions and emission angles:

$$d_i\left(\Delta \phi ,\Delta \theta \right)=\sum _{j=0}^{J-1}\sum _{k=0}^{K-1}{\dot{D}}_{i,j,k}\left(\Delta \phi ,\Delta \theta \right)t_{j,k},$$ (1)

where t_j,k is the dwell time, which is always greater than or equal to zero, for which the source is pointed in direction φ_k while it is located at dwell position j. The source step length along the source trajectory, Δλ, was set to 3 mm. We also considered the cases in which Δλ was 1, 6, and 8 mm. As with φ_k, ${\dot{D}}_{i,j,k}\left(\Delta \phi ,\Delta \theta \right)$ and t_{j, k} are periodic functions of the index k with a period of K.

The RSBT source was assumed to be a 50 kVp Xoft Axxent^TM with a 0.5 mm tungsten shield providing less than 0.1% transmission. RSBT beamlets were obtained by multiplying unshielded 3D dose rate distributions obtained using the TG-43 dose calculation model of Rivard et al.⁸ by a binary function that was zero at all points blocked by the shield and unity at all other points. Thus, the point source approximation was used and the effects of emission angle size on the x-ray scatter component of the Xoft Axxent^TM dose distribution were neglected. The approximations are justified since the azimuthal emission angle selection method can be applied regardless of the accuracy of the beamlet calculation technique. The exact result of the method will likely have a slight, although unknown, dependence on the beamlet calculation technique.

In order to demonstrate the characteristics of the clinical cases used in this study, the conventional intracavitary (ICBT) treatment plans for each case were also simulated. A tandem and ring (radius = 21.25 mm) applicator with ¹⁹²Ir was used for ICBT.

The emission angle selection problem was limited to azimuthal angles, and the zenith angle was held constant throughout the current work at Δθ = 120°. It is assumed that the source emission direction would be controlled by rotating the shield about the source, and that the x-ray intensity of the unshielded source has no azimuthal dependence.

Clinical cases, treatment goals, and plan quality metrics

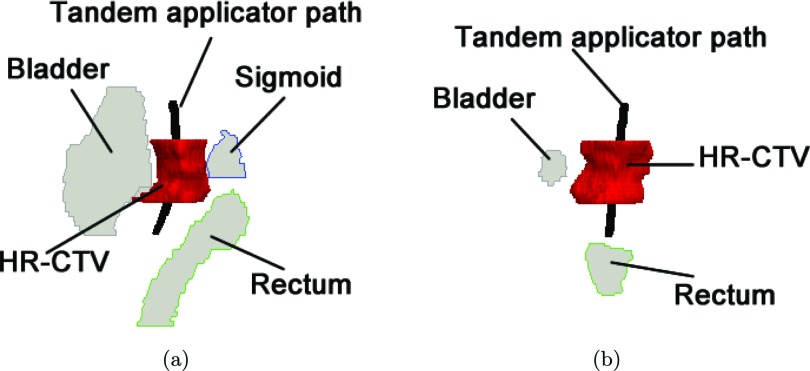
Treatment plans were based on two cervical cancer cases, previously treated with MR-guided BT. For each patient, the RSBT was simulated to be delivered through a single-channel tandem applicator without a ring applicator. An example of the anatomical area treated is shown in Fig. 2. The high-risk clinical target volume (HR-CTV) and rectum, sigmoid colon, and bladder OARs were delineated by a radiation oncologist using the GEC-ESTRO recommendations.¹ The HR-CTVs were larger than 40 cm³. Prior EBRT doses of 45 Gy in 25 fractions (fx) of 1.8 Gy were delivered to the HR-CTV and OARs for both patients, which was accounted for in the BT treatment planning. The BT delivery was assumed to take place over five fractions, which is standard at the authors’ institution. The HR-CTV doses [Gy₁₀] and OARs doses [Gy₃] were expressed as equivalent doses in 2 Gy fraction of EBRT (EQD2),¹⁷ using α/β values of 10 and 3 Gy, respectively.² In Sec. 3B, the HR-CTV and OARs doses will be measured with EQD2 and the subscripts will be omit for brevity.

Figure 2.

(a) Sagittal and (b) coronal view of a test clinical cervical cancer case.

The RSBT and conventional (unshielded) BT treatment goal was to escalate tumor dose without exceeding the OAR tolerances and the delivery time budgets. Specifically, the minimum dose received by 90% of the HR-CTV (D₉₀) was maximized under the constraint that the minimum doses to the hottest 2 cm³ (D_2cc) of the rectum, sigmoid colon, and bladder could not exceed the tolerance doses^{2, 4} of 75, 75, and 90 Gy, respectively. The Δφ-dependent treatment plan quality metrics were D₉₀ for the HR-CTV and the delivery time. As the delivery time for EBRT was assumed invariant for all cases and planning methods, only the delivery time for BT is considered in this study.

Generating beamlets by combining baseline beamlets

It was assumed that the baseline azimuthal angle, δφ, was small enough that all shield azimuthal angles were integer multiples of it. It was also assumed that the shield window can only be aligned with directions which are integer multiples δφ. Baseline beamlets are defined as the beamlets generated using the baseline azimuthal angle δφ. According to the study conducted by Ebert,⁵ the quality of dose coverage tends to be better with smaller δφ yet requires more time for optimization due to the increased degrees of freedom. In order to strike a balance between the quality and computation time, we set δφ to 11.25° for this work which resulted in 32 possible azimuthal emission angles.

The baseline beamlets at a given dwell position j are assumed to be nonoverlapping; thus, the shadows cast by the shields of neighboring beamlets (k and k + 1 for a given dwell position j) do not overlap. An integer number, W (W > 1), of neighboring baseline beamlets can be combined by superposition to produce a beamlet with a larger azimuthal emission angle, Δφ_W = W δφ, as follows:

$${\dot{D}}_{i,j,k}\left(\Delta {\phi }_W,\Delta \theta \right)=\sum _{p=0}^{W-1}{\dot{D}}_{i,j,k+p}\left(\delta \phi ,\Delta \theta \right),$$ (2)

generating a set of “W-beamlets.” Equation 2 is exact for the case of zero shield transmission, which is a safe assumption for the case under consideration.

Consider the case in which the W neighboring baseline beamlets, with indices from k to k + W − 1, all share delivery times of t_{j, k} = τ. It follows from Eq. 2 that the W neighboring beamlets can be replaced with a single beamlet with an azimuthal emission angle Δφ_W and a delivery time of $t_{j,k}^W=\tau ,$ where the t-superscript indicates that the delivery time is associated with a beamlet with an emission angle of Δφ_W. Conversely, a beamlet with an azimuthal emission angle of Δφ_W and a delivery time of τ can be replaced with the baseline beamlets with indices between k and k + W − 1, which will have delivery times of $t_{j,k}^1=\tau$. Thus, an entire set of dwell times associated with beamlets of azimuthal emission angle Δφ_W can be written as a set of baseline dwell times (W = 1) as follows:

$$t_{j,k}^{W\to 1}=\sum _{k^{\prime }=0}^{K-1}{t}_{j,k^{\prime }}^W\Pi \left[\frac{\left(k-k^{\prime }\right)\mathrm{mod}K}{W}\right],$$ (3)

where Π(a/W) is unity when 0 ≤ a < W (a and W are both integers) and zero otherwise. The Π-function spreads the dwell times from the Δφ_W azimuthal emission angle beamlets over multiple baseline beamlets. The modular arithmetic in its argument makes Π a periodic function of k′ with period K. Equation 3 can be simplified by changing summation indices for k′ to p = k − k′ as follows:

$$t_{j,k}^{W\to 1}=\sum _{p=0}^{K-1}{t}_{j,k-p}^W\Pi \left(\frac{p\mathrm{mod}K}{W}\right)=\sum _{p=0}^{W-1}{t}_{j,k-p}^W.$$ (4)

Since the sum over k′ in Eq. 3 is over one period $t_{j,k-p}^W,$ which is a periodic function of k′, the summation over p in the middle expression of Eq. 4 can be done over the same range, even after changing variables.

Treatment plan generation from anchor plans

A treatment plan generated using the W-beamlets (W > 0) and an in-house dose-volume optimizer is denoted by ${\widehat{P}}^W$, which has a dwell time of ${\widehat{t}}_{j,k}^W$ and a dose distribution ${\widehat{d}}_i^W$. The in-house dose-volume optimizer used in this study is a simulated annealing optimizer which is aimed at maximizing the HR-CTV D₉₀ while keeping the D_2cc of all OARs below the GEC-ESTRO recommended thresholds. In order to make the simulated annealing algorithm efficient, the initial solution was generated by a linear least squares method to optimize the dose homogeneity on the HR-CTV surface.¹⁸ Both the simulated annealing method^{5, 16} and the linear least squares method^{19, 20, 21, 22} have been used for treatment planning in previous studies. The baseline equivalent plan of ${\widehat{P}}^W$ is denoted as ${\widehat{P}}^{W\to 1}$, which has a dwell time of ${\widehat{t}}_{j,k}^{W\to 1}$ for baseline beamlets and the same dose distribution ${\widehat{d}}_i^W$.

As the dose-volume optimization is a nonconvex optimization, the simulated annealing optimizer still requires 5–10 min to converge even with initial guesses from the linear least squares method. Therefore, it is challenging to generate plans with all possible W-values in times appropriate for clinical application. The proposed solution is to limit the number of calls to the optimizer, and to achieve this, the concept of anchor RSBT plans is introduced.

An anchor plan ${\widehat{P}}^W$ for a given patient is the treatment plan generated with W-beamlets, by finding ${\widehat{t}}_{j,k}^W$, which is the optimal $t_{j,k}^W$ for (j = 0, …, J − 1, k = 0, …, K − 1). The baseline equivalent plan ${\widehat{P}}^{W\to 1}$ can then be obtained directly from ${\widehat{P}}^W$ without modifying the delivered dose distribution, ${\widehat{d}}_i^W$. Then, an expedient treatment plan ${\tilde{P}}^{W^{\prime }}$, which has a dwell time of ${\tilde{t}}_{j,k}^{W^{\prime }}$, is rapidly generated from an anchor plan ${\widehat{P}}^W$ by solving the following optimization problem:

$$\begin{array}{ccc}& & \min \sum _{j=0}^{J-1}\sum _{k=0}^{K-1}({\lambda }_{j,k}^{-}H\left({\widehat{t}}_{j,k}^{W\to 1}-{\tilde{t}}_{j,k}^{W^{\prime }\to 1}\right)\hfill \\ & & +{\lambda }_{j,k}^{+}H\left({\tilde{t}}_{j,k}^{W^{\prime }\to 1}-{\widehat{t}}_{j,k}^{W\to 1}\right)){\left({\tilde{t}}_{j,k}^{W^{\prime }\to 1}-{\widehat{t}}_{j,k}^{W\to 1}\right)}^2\hfill \\ & & \mathrm{s}.\mathrm{t}.{\tilde{t}}_{j,k}^{W^{\prime }\to 1}=\sum _{p=0}^{W-1}{\tilde{t}}_{j,k-p}^{W^{\prime }}\hfill \\ & & \sum _{j=0}^{J-1}\sum _{k=0}^{K-1}{\tilde{t}}_{j,k}^{W^{\prime }}\le T_{max},\hfill \end{array}$$ (5)

where H(x) is a Heaviside function and ${\lambda }_{j,k}^{+}$ and ${\lambda }_{j,k}^{-}$ are coefficients for overdosing and underdosing at dwell position ${\stackrel{\rightharpoonup }{s}}_j$ and emission direction φ_k of the baseline beamlet, respectively. In this study, ${\lambda }_{j,k}^{+}$ is proportional to the largest dose rate contribution [i.e., ${\max }_{\mathrm{i}\in \mathrm{OAR}}{\dot{D}}_{i,j,k}\left(\delta \phi ,\Delta \theta \right)$] to the OAR of the corresponding beamlet, and ${\lambda }_{j,k}^{-}$ is proportional to the largest dose rate contribution to the HR-CTV surface [i.e., ${\max }_{\mathrm{i}\in \mathrm{HR}-\mathrm{CTV}\_\mathrm{surface}}{\dot{D}}_{i,j,k}\left(\delta \phi ,\Delta \theta \right)$].

Due to the inevitable disagreement between ${\widehat{t}}_{j,k}^{W\to 1}$ and ${\tilde{t}}_{j,k}^{W^{\prime }\to 1}$ in most real-world cases, ${\tilde{P}}^{W^{\prime }}$ may not reproduce the dose distribution of ${\widehat{P}}^W$ perfectly. The plan quality tends to degenerate as W′ increases. As a result, the expedient plan ${\tilde{P}}^{W^{\prime }}$ can be regarded as an approximation of the dose-volume optimized plan ${\widehat{P}}^W$. However, the approximation quality will decrease as W′ increases.

With the solution to Eq. 5, ${\tilde{t}}_{j,k}^{W^{\prime }}$ is scaled to maximize D₉₀ in the HR-CTV as described in Sec. 2B. T_max is a constraint on the total delivery time of ${\tilde{P}}^{W^{\prime }}$ which can be imposed to reduce treatment time at the expense of HR-CTV D₉₀. Obtaining ${\tilde{P}}^{W^{\prime }}$ by solving the sequencing problem in Eq. 5 is faster than the full optimization needed to obtain ${\widehat{P}}^{W^{\prime }},$ since the problem concerns dwell times only, rather than dwell times and beamlets.

To enable a balance between the time costs spent on exhaustive reoptimization and the plan quality, a small set of anchor plans ${\widehat{P}}^8$, ${\widehat{P}}^{16}$, and ${\widehat{P}}^{24}$ was chosen. The corresponding azimuthal emission angles are 90°, 180°, and 270°, evenly spaced among all possible azimuthal emission angles and can be considered a sparse sampling of the full-set of simulated-annealing optimized plans. The time budget for each anchor plan used in this study is 5 min, therefore, the overall time cost for three anchor plans and the REAS technique will be comparable to the overall time cost for the exhaustive surface optimization.

The optimal sequencing is then applied to each anchor plan and a delivery efficiency curve, which is a Pareto-front²³ showing the trade-off between D₉₀ and delivery times for all possible Ws, is generated.

Evaluation and comparison

To evaluate a planning method, the planning time and the plan quality were considered. The plan quality was established by maintaining a balance between the HR-CTV D₉₀ and the corresponding delivery time under the constraint that all OAR D_2cc values are below tolerance. By plotting the best HR-CTV D₉₀ achieved by the planning method against specified delivery time budgets, we generated a delivery efficiency curve for the planning method. For the purpose of comparison, three different planning methods including REAS were applied to two clinical cases (see Fig. 3):

1. ERVO. With this method, the in-house dose-volume optimizer, using both the linear least square method and simulated annealing, was applied to all W-beamlets.

2. ERSO. Using this method, only the linear least square method was applied at all W-beamlets.

3. REAS, based on three anchor plans with azimuthal emission angles 90°, 180°, and 270°.

Figure 3.

TPS processes for REAS method. Two distinct workflows are shown: (1) ERVO and ERSO method are shown by solid and dotted lines; (2) REAS method is shown by solid and dashed lines. These two methods are also different in the number of Ws for the initial input, the ERVO and ERSO methods need all possible Ws, while REAS method needs only a small subset.

For each clinical case and each planning method, a corresponding delivery efficiency curve was generated instead of a single plan. When using the ERVO method, for example, the dose optimization with simulated annealing was applied to all 32 possible azimuthal emission angles. For each azimuthal emission angle, a delivery plan was generated with a delivery time (x-axis) and a HR-CTV D₉₀ (y-axis). We called these plans (calculated directly with the dose optimizer or optimal sequencing) prime plans. Each prime plan corresponds to a single point on the delivery efficiency plot. The prime plans can be scaled with any scaling factor less than 1, resulting in a derived plan. A derived plan will have lower D₉₀ and lower delivery time compared to the prime plan and the OAR dose will still be kept below the given threshold. All derived plans from the same prime plan will be shown as a curve on the delivery efficiency plot which was generated by finding the envelope of all 32 curves. The delivery efficiency curves for ERSO were generated by a similar method as described for ERVO, except that the dose optimization was performed using the linear least square method only. For the REAS method, we used 3 × 32 prime plans instead of 32 as we applied the optimal sequencing to each anchor plan and each azimuthal emission angle.

There are two ways to interpret a delivery efficiency curve: (i) Given a D₉₀ goal (y-axis), the most appropriate delivery plan can be found at the leftmost point on the curve that is above the horizontal line (y = D₉₀ goal). According to the delivery efficiency curve, this point represents the minimal delivery time required to achieve the specified D₉₀. The azimuthal emission angle will be determined by the delivery plan corresponding to this point, and no other azimuthal emission angles can achieve less delivery time with the specified D₉₀ satisfied. Thus, for different planning methods with same D₉₀ goal on the same case, the selected azimuthal emission angle may or may not be the same. (ii) Given a delivery time budget (x-axis), the most appropriate delivery plan can be found at the top most point on the curve that is on the left of the vertical line (x = time budget). This point represents the highest D₉₀ that can be achieved within the given time budget. The azimuthal emission angle will be determined by the delivery plan corresponding to this point, and no other azimuthal emission angles can achieve higher D₉₀ within the given time budget. Thus, for different planning methods with same delivery time budget on the same case, there is no guarantee that the selected azimuthal emission angle would be the same.

Therefore, besides the visual comparison between delivery efficiency curves, these three methods were also quantitatively compared by

1. The average minimal delivery time for all D₉₀ goals in a selected set of interest. The selected set consists of every integral valued at D₉₀ from 85 to 100 Gy. The reason for selecting this interval is that: (1) a plan with D₉₀ less than 85 Gy may not be good enough to be clinically useful; (2) for the cases studied in this work, the delivery time for a plan with D₉₀ higher than 100 Gy is too high to be practical in most cases. If the desired D₉₀ cannot be achieved, changes to the delivery time will be considered as the means to achieving the maximal D₉₀ for this method during the computation.

2. The average maximal D₉₀ for all delivery time budgets in a selected set of interest. The selected set consists of every integral valued delivery time from 5 to 25 min/fx for patient #1, and 10 to 30 min/fx for patient #2. These intervals were selected on the basis of keeping both D₉₀ and the delivery time in the clinically reasonable range. The range of delivery time budgets varied due to geometrical variations in the HR-CTV and the applicator location between clinical cases was also seen to vary. In the first case with a D₉₀ ≈ 86 Gy and under a 5 min delivery time budget, we were able to achieve a reasonable clinical delivery plan. However, in the second case, under a 5 min time budget all three methods were only able to provide plans with a D₉₀ ≈ 60 Gy which is not clinically reasonable. Thus, we excluded those points which were considered as “of no interest.”

RESULTS

Planning time comparison

The ERVO method took about 3 h to finish and was the most time-consuming method among the three methods studied in this work. The time costs for the ERSO and the REAS method were approximately the same at about 20 min. All three methods were applied to all 32 different azimuthal emission angles and were able to generate the corresponding delivery efficiency curve.

When using the ERVO method, the time spent on dose optimization using the simulated annealing algorithm dominated the time cost, as each dose optimization took 5 min. For all 32 plans the ERVO method (W = 1,…,32) took about 3 h, including the time for computing the beamlets. It is important to note that the running time for the ERVO method depends on the preassigned computation time budgets as there is no guaranteed time for achieving an optimal solution with a simulated annealing based algorithm.

Because the ERSO method took less time; the whole procedure can be finished in around 20 min for all 32 plans including the time needed to compute the beamlets.

The REAS optimal sequencing process required less than a second for each sequence. The time needed to generate the anchor plans, around 15 min for all three anchor plans, dominates the time cost for this process. The whole REAS process, including the time spent on beamlet calculation, can be finished in about 20 min.

Plan quality comparison

We evaluated the conventional plans for both cases studied in this paper, and the results are shown in Table 1. In both cases, the conventional intracavitary method can only achieve D₉₀ less than 87 Gy, which may result in suboptimal treatment outcomes.²⁴

Table 1.

List of conventional ICBT plans that were evaluated with HR-CTV D₉₀, OAR D_2cc, and the delivery times.

	HR-CTV	Bladder	Sigmoid	Rectum	Delivery
Patient	D90 (Gy)	D2cc (Gy)	D2cc (Gy)	D2cc (Gy)	time (min/fx)
#1	74.5	90.0	64.8	55.7	4.6
#2	77.2	90.0	52.0	67.2	5.3

For the three RSBT planning methods studied in this paper, delivery efficiency curves were generated instead of single plans. The delivery efficiency curves for each patient with the three planning methods are shown in Fig. 4.

Figure 4.

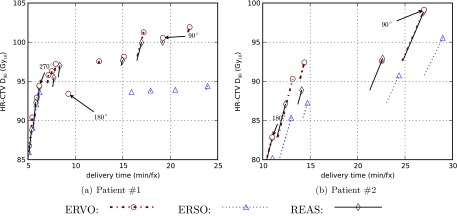
Delivery efficiency curves for two clinical cases by using three different RSBT planning methods. The anchor plans are explicitly labeled with the corresponding azimuthal emission angles even if they are not on the delivery efficiency curves.

As seen in Fig. 4, the curves generated when using the ERVO method always appear in the top-left-most position indicating that the ERVO method generates plans with best quality. The curves generated using the REAS method lie in-between the corresponding curves generated by the ERVO and the ERSO method, showing that REAS may be regarded as a better way of approximating ERVO compared with ERSO.

According to the results as seen in Table 2, the delivery time when using the ERSO method for patient #1 averaged 5.6 min/fx more than that when using the ERVO method, with a range from −0.1 to 17.6 min/fx with a D₉₀ goal set to 85–100 Gy. Using the REAS method, the delivery time increased 0.8 min/fx on average over that achieved by using the ERVO method, with an increased range between −0.1 and 6.9 min/fx. This demonstrates that with the same D₉₀ goal, the delivery time of the plan computed by the REAS method is less than that achieved by the ERSO method. On average, REAS needs 21% less delivery time than ERSO in this case.

Table 2.

A part of the dosimetric comparison for patient #1 between ERVO, ERSO, and REAS methods with D₉₀ goals set to 85–100 Gy. The average delivery time was computed for all D₉₀ goals in the range with 1 Gy spacing, and if the specified D₉₀ goal could not be achieved, the delivery time with the best D₉₀ is used instead and the delivery time will be marked with an * mark.

		Achieved	Bladder	Sigmoid	Rectum	Delivery	Azimuthal emission
D90 goal (Gy)		D90 (Gy)	D2cc (Gy)	D2cc (Gy)	D2cc (Gy)	time (min/fx)	angle Δφ (deg)
85	ERVO	85.00	87.57	52.45	70.28	4.96	303.75
	ERSO	85.00	88.69	52.63	70.20	5.02	303.75
	REAS	85.00	86.54	55.77	74.22	4.89	303.75
90	ERVO	90.00	89.41	53.67	73.15	5.43	292.50
	ERSO	90.00	84.34	57.07	73.42	5.70	281.25
	REAS	90.00	87.37	55.51	73.11	5.62	281.25
95	ERVO	95.00	89.13	57.60	74.36	7.08	236.25
	ERSO	94.43*	83.03	55.60	74.74	23.95	67.50
	REAS	95.00	82.85	55.67	74.62	7.69	213.75
100	ERVO	100.00	88.67	57.31	74.21	16.92	101.25
	ERSO	94.43*	83.03	55.60	74.74	23.95	67.50
	REAS	100.00	89.94	55.90	74.03	19.18	90.00
Average delivery time ERVO: 7.9 min/fx, ERSO: 13.5 min/fx, REAS: 8.7 min/fx

Table 3 shows results after the delivery time budget was changed from 5 to 25 min/fx. For patient #1, the difference between the D₉₀ achieved using the REAS method and the ERVO method was −0.8 Gy on average; with differences ranging between −0.5 and 1.9 Gy. By comparison, the difference between the D₉₀ achieved using the ERSO method and the ERVO method was −5.0 Gy; and the difference ranged between −8.0 and −0.6 Gy.

Table 3.

A part of the dosimetric comparison for patient #1 between ERVO, ERSO, and REAS methods with time budget set to 5–25 min/fx. The averages of delivery time were computed on all delivery time budgets in the range with 1 min/fx spacing.

Time budget		Achieved	Bladder	Sigmoid	Rectum	Delivery	Azimuthal emission
(min/fx)		D90 (Gy)	D2cc (Gy)	D2cc (Gy)	D2cc (Gy)	time (min/fx)	angle Δφ (deg)
5	ERVO	85.42	88.10	52.55	70.59	5.00	303.75
	ERSO	84.82	88.46	52.59	70.07	5.00	303.75
	REAS	85.88	90.00	52.72	67.66	4.97	303.75
10	ERVO	97.27	90.00	57.85	74.93	7.94	213.75
	ERSO	93.63	90.00	56.09	74.84	6.23	270.00
	REAS	96.99	89.04	55.40	75.00	8.36	202.50
15	ERVO	97.56	89.93	58.51	75.00	12.50	135.00
	ERSO	93.63	90.00	56.09	74.84	6.23	270.00
	REAS	97.70	90.00	56.22	74.42	14.96	112.50
20	ERVO	101.28	89.87	57.64	75.00	17.19	101.25
	ERSO	93.86	82.26	56.22	75.00	17.94	90.00
	REAS	100.06	90.00	55.98	74.68	19.19	90.00
25	ERVO	101.93	89.99	56.22	75.00	22.04	78.75
	ERSO	94.43	83.37	55.61	75.00	23.95	67.50
	REAS	100.06	90.00	55.98	74.68	19.19	90.00
Average achieved D90 ERVO: 98.2 Gy, ERSO: 93.3 Gy, REAS: 97.6 Gy

For patient #2, the D₉₀ goals ranged between 85 and 100 Gy and the detailed data are shown in Table 4. The average delivery time when using the ERSO method increased 10.2 min/fx compared to that achieved by ERVO, with an increase of between 0.9 and 16.8 min/fx; while REAS only increased the delivery time by on average 2.4 min/fx, with a range of −0.1–8.6 min/fx. The REAS method required on average 20% less delivery time than the ERSO method.

Table 4.

Dosimetric comparison for patient #2 between ERVO, ERSO, and REAS methods with D₉₀ goals set to 85–100 Gy. The average delivery time was computed on all D₉₀ goals in the range using 1 Gy spacing. If the specified D₉₀ could be achieved, the delivery time with the best D₉₀ is used instead and the delivery time will be marked with an * mark.

		Achieved	Bladder	Sigmoid	Rectum	Delivery	Azimuthal emission
D90 goal (Gy)		D90 (Gy)	D2cc (Gy)	D2cc (Gy)	D2cc (Gy)	time (min/fx)	angle Δφ (deg)
85	ERVO	85.00	83.69	70.81	56.28	12.05	168.75
	ERSO	85.00	88.58	74.68	53.24	12.92	157.50
	REAS	85.00	87.28	52.94	49.34	11.96	168.75
90	ERVO	90.00	89.58	74.74	53.39	13.10	168.75
	ERSO	90.00	89.07	68.66	51.60	24.08	90.00
	REAS	90.00	82.90	72.85	52.00	21.67	101.25
95	ERVO	95.00	85.87	72.34	52.64	25.57	90.00
	ERSO	95.00	89.40	66.35	51.84	28.75	78.75
	REAS	95.00	85.87	72.34	52.64	25.57	90.00
100	ERVO	100.00	81.94	69.73	53.29	30.46	78.75
	ERSO	98.07*	90.00	66.39	52.14	42.48	56.25
	REAS	100.00	84.48	71.81	52.29	30.92	78.75
Average delivery time ERVO: 19.7 min/fx, ERSO: 28.1 min/fx, REAS: 22.1 min/fx

When considering D₉₀ with respect to a given delivery time using a range of 10–30 min/fx (our patient #2), the average D₉₀ achieved when using REAS was 1.5 Gy less than that achieved when using ERVO. When using the ERSO method, it was decreased by 4.6 Gy as compared to ERVO. The D₉₀ increases the range from −0.3 to 3.5 Gy when using REAS; while the range was between 2.3 and 8.3 Gy when using ERSO. On average, REAS achieved 3.1 Gy higher D₉₀ than ERSO. Detailed data are shown in Table 5.

Table 5.

Dosimetric comparison for patient #2 between ERVO, ERSO, and REAS methods with time budget set to 10–30 min/fx. The average delivery times were computed on all delivery time budgets using a range with 1 min/fx spacing.

Time budget		Achieved	Bladder	Sigmoid	Rectum	Delivery	Azimuthal emission
(min/fx)		D90 (Gy)	D2cc (Gy)	D2cc (Gy)	D2cc (Gy)	time (min/fx)	angle Δφ (deg)
10	ERVO	78.15	83.19	66.24	55.60	10.00	180.00
	ERSO	75.81	83.08	62.43	52.26	10.00	168.75
	REAS	78.15	83.19	66.24	55.60	10.00	180.00
15	ERVO	92.44	89.99	75.00	56.45	14.40	157.50
	ERSO	87.26	90.00	72.75	53.98	14.72	146.25
	REAS	88.90	90.00	74.86	57.25	14.12	157.50
20	ERVO	92.44	89.99	75.00	56.45	14.40	157.50
	ERSO	87.26	90.00	72.75	53.98	14.72	146.25
	REAS	88.90	90.00	74.86	57.25	14.12	157.50
25	ERVO	93.40	84.32	71.32	52.35	25.00	90.00
	ERSO	90.78	90.00	69.15	51.74	24.38	90.00
	REAS	93.40	84.32	71.32	52.35	25.00	90.00
30	ERVO	99.14	89.91	75.00	53.40	27.02	90.00
	ERSO	95.57	90.00	66.63	51.93	28.98	78.75
	REAS	99.14	89.91	75.00	53.40	27.02	90.00
Average achieved D90 ERVO: 92.2 Gy, ERSO: 87.6 Gy, REAS: 90.8 Gy

In both cases studied in this paper, the REAS method resulted in about 20% less delivery time than ERSO with the same D₉₀ goal. REAS could boost the D₉₀ contribution for BT by over 5% on average while compared to the ERSO method. All three RSBT planning methods were able to achieve higher HR-CTV D₉₀ than the conventional ICBT method, at the cost of longer treatment times.

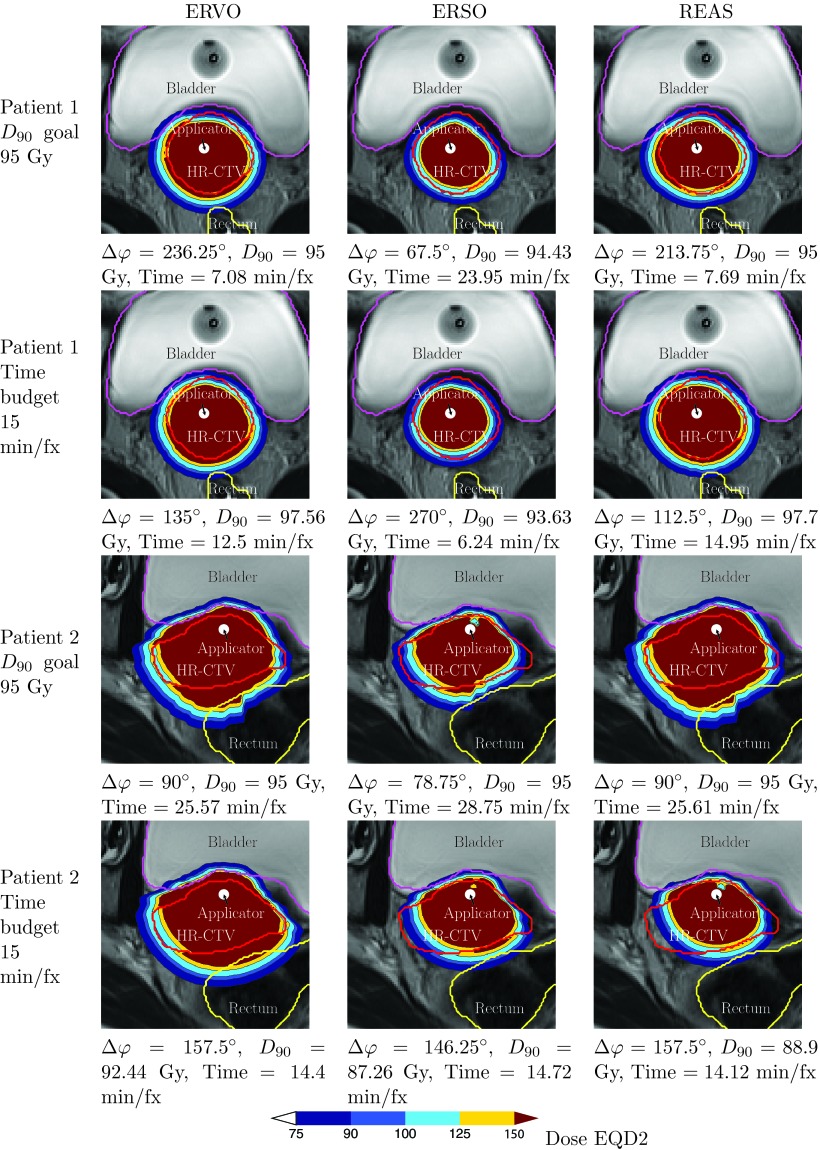
To graphically represent the differences that these plans generated when using the three methods studied in this paper, we included a dose distribution plot on a single 2D slice for each method and each patient case, as seen in Fig. 5.

Figure 5.

EQD2 dose distributions on a 2D slice generated by three different planning methods for two patients with selected D₉₀ goal or delivery time budget. The positions of tandem applicator are shown with the black circles inside the HR-CTV regions.

DISCUSSION

By combining dose-volume optimization with the sequencing algorithm, the REAS method provides users a tool by way of the delivery efficiency curves to facilitate treatment planning in a reasonable time frame. Theoretically, the ERVO method can also provide users with the quality tools needed but at the cost of far greater computational times. The quality of the plans produced when using the REAS method is superior to those generated by ERSO according to the results of this study, and may be considered a closer approximation to the ERVO method than the ERSO method.

The dosimetric results were insensitive to the dwell position spacing, Δλ, as long as the combination of Δλ and Δθ does not lead to cold spots, i.e., Δλ ≤ 2r·tan(Δθ/2), where r is the radius of the applicator. Compared with the cases with a Δλ of 3 mm, the HR-CTV D₉₀ values for the baseline plans were increased by about 0.5% with a Δλ of 1 mm. With Δθ set to 120° and an r of 3.2 mm, cold spots appear when Δλ is greater than 5.5 mm. By changing Δλ to 6 mm, the HR-CTV D₉₀ values were decreased by about 5% due to the presence of cold spots near the applicator. With a Δλ of 8 mm, cold spots will reduce the HR-CTV D₉₀ by 50% relative to those with a Δλ of 3 mm.

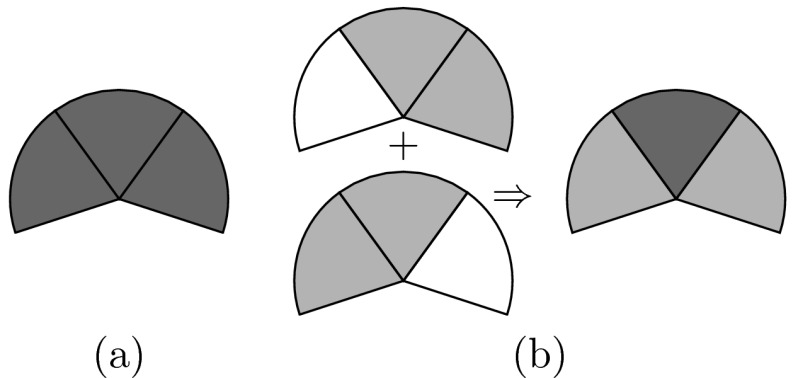
The delivery efficiency curves seen in Fig. 4 provide more information than simply describing the tradeoff between delivery time and dose quality. Based on our experimental results we found that: first, the delivery efficiency curves vary between cases, showing the selection of the azimuthal emission angle Δφ should be case-dependent. Second, smaller azimuthal emission angles do not guarantee better dose distributions. This conclusion seems to be counterintuitive, yet a simple explanation is that we are using a fixed azimuthal emission angle. If the larger azimuthal emission angle is not a multiple of the smaller one, we cannot always expect to get a better dose distribution by using the smaller angle. Supposing that Fig. 6a shows the ideal dose distribution, then the dose distribution can be perfectly reproduced by set Δφ = 3δφ. However, with a smaller azimuthal emission angle Δφ = 2δφ, it is impossible to perfectly reproduce the dose distribution, as shown in Fig. 6b. Third, we selected three anchor plans in this study and the REAS method worked well for interpolating between anchor plans. However, for the regions of interest, where both delivery time and D₉₀ fall into clinically reasonable intervals, a single or two anchor plans dominated in most cases. In this study, the anchor plan which was effective in most cases is the one with Δφ = 90° as illustrated by Fig. 7. Compared to the ones generated by three anchor plans, the delivery efficiency curves generated by a single plan were slightly inferior, however, the differences might be an acceptable trade-off for reducing the planning time. As mentioned in Sec. 2D, the REAS method tries to approximate the baseline equivalent dwell time series ${\widehat{t}}_{j,k}^{W\to 1}$ of the anchor plans as much as possible. However, due to the increase in the azimuthal emission angle, the baseline equivalent dwell time series of the plans after applying the REAS method, ${{\tilde{t}}_{j,k}}^{W^{\prime }\to 1}$, tend to be smoothed. Although our studies show that the weighted Heaviside function in the objective has effectively reduced the requirement on the smoothness of ${\widehat{t}}_{j,k}^{W\to 1}$, those anchor plans which are “smoother” may have a better chance of preserving the plan quality when being sequenced with a relatively large parameter W. Therefore, the REAS method studied in this paper can also benefit from any improvement to the dose optimizer which may increase the dose quality or smooth the time sequence.

Figure 6.

Situation in which a smaller azimuthal emission angle results in a worse dose distribution. (a) A dose distribution that can be perfectly reproduced with Δφ = 3δφ. (b) By using Δφ = 2δφ, it is impossible to perfectly reproduce the dose distribution shown in (a).

Figure 7.

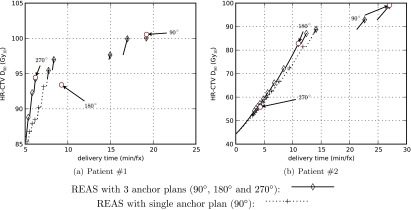
Delivery efficiency curves for two clinical cases by using different set of anchor plans. Three anchor plans (90°, 180° and 270°) are explicitly labeled with the corresponding azimuthal emission angles.

Although we only considered a single tandem applicator for all the RSBT planning within this work, the REAS method introduced here would also benefit from use in a multiple channel device such as those used in a tandem and ovoid applicator.

The RSBT system may be clinically implemented by using detachable partial shields. To fully exploit the potential of the REAS method, a set of different shields with all possible azimuthal emission angles is desired. In the cases studied in this work, this requirement leads to 30 different shields. While too many different shields may be economically inefficient for a clinical implementation, the number of shields may be reduced by using a subset of all possible azimuthal emission angles instead of the universal set. It was observed that more than 80% of the plans on the delivery efficiency that were clinically reasonable can be covered by azimuthal emission angles between 90° and 270°. Making use of this observation can reduce about half of the shields and make the required shields less than 20. The number of shields can be further reduced by increasing δφ. For example, with δφ = 22.5°, only nine shields are needed to cover the angles from 90° to 270°.

CONCLUSIONS

Using the REAS technique introduced in this study, RSBT users will be able to strike a balance between the treatment time and the dose quality about 10 times faster than when using exhaustive dose-volume optimizations. The loss of plan quality, measured by both the treatment time and the HR-CTV D₉₀, is maintained at a low level. Compared to the ERSO method which requires a similar amount of computational time, the REAS method can reduce the treatment time by about 20% while maintaining the HR-CTV D₉₀, or boost the D₉₀ by about 5% while maintaining the same delivery time.

Rotating-shield brachytherapy planning may benefit from the REAS technique and is more likely than conventional ICBT to yield better plans in the limited time available. Moreover, RSBT users will have the freedom to optimize the tradeoff between the delivery time and the HR-CTV dose conformity with RSBT by the selection of the azimuthal emission angle.