Estimating T₁ from Multichannel Variable Flip Angle SPGR Sequences

Abstract

Quantitative estimation of T₁ is a challenging but important task inherent to many clinical applications. The most commonly used paradigm for estimating T₁ in vivo involves performing a sequence of spoiled gradient-recalled echo acquisitions at different flip angles, followed by fitting of an exponential model to the data. Although there has been substantial work comparing different fitting methods, there has been little discussion on how these methods should be applied for data acquired using multichannel receivers. In this note, we demonstrate that the manner in which multichannel data is handled can have a substantial impact on T₁ estimation performance and should be considered equally as important as choice of flip angles or fitting strategy.

INTRODUCTION

The relaxation time T₁ defines the rate of recovery of longitudinal magnetization of spins in a tissue toward equilibrium after radio frequency excitation. Quantitative knowledge of T₁ is useful for many clinical applications, including: (1) optimizing pulse sequences to generate contrast between tissues of interest; (2) estimating perfusion rate constants like K^trans in dynamic contrast-enhanced MRI (1); (3) monitoring pathology and treatment efficacy (2,3); and (4) guidance for automated image segmentation (4). Although T₁-weighted images can be readily acquired, generating accurate quantitative estimates of the T₁ values of tissues is not as straightforward. The “gold standard” for T₁ mapping is two-dimensional spin echo inversion recovery (5-7); however, this approach is too slow for in vivo clinical applications. Look–Locker techniques (8,9) are faster than IR, but still time consuming and nontrivial to implement. Variable flip angle (VFA) spoiled gradientrecalled echo (SPGR) sequences (10-15) are commonly used for in vivo T₁ mapping due to their time and signalto-noise ratio (SNR) efficiency [even when accounting for B₁ inhomogeneity (16)], and straightforward implementation. Because of their ubiquity, we focus on the VFA–SPGR approach to T₁ mapping in this work.

In the literature, there has been substantial discussion on what numerical fitting strategy to use for estimating T₁ from a VFA–SPGR sequence. However, there has been essentially no discussion on how these methods should be applied for data acquired with multichannel receivers. In this work, we investigate several approaches for handling multichannel data during T₁ estimation and demonstrate that this seemingly innocuous processing step can substantially impact T₁ estimation performance.

THEORY

The VFA–SPGR Signal Model

Consider an MRI experiment where the object of interest is probed using a fully sampled, fully spoiled, Cartesian SPGR sequence with nominal flip angle θ, repetition time TR, echo time, and (relative) transmit radiofrequency field B₁, and where the generated MR signal is observed by a N_c-element phased array or multichannel receiver (17). Let Ω denote the (discrete) set of pixels tiling the prescribed field-of-view. Assuming that B₁ is (approximately) known a priori, at pixel x ∈ Ω, flip angle index i = 1, …, N_i, and for receiver channel c = 1, …, N_c, the reconstructed discrete image series can be modeled as:

$$g(x,c,i)=m_0(x)s(x,c)\frac{\sin (\widehat{\mathrm{\theta }}(x,i))(1-e^{-\mathrm{TR}/T_1(x)})}{1-\cos (\widehat{\mathrm{\theta }}(x,i))e^{-\mathrm{TR}/T_1(x)}}+z(x,c,i),$$ [1]

where m₀(x) is a complex variable that is proportional to tissue spin density, s(x, c) is the sensitivity function for the cth receiver coil, θ̂(x, i) = θ(i)B₁(x) is the effective flip angle and z(x, c, i) is complex Gaussian noise. In this work, noise is assumed to be uncorrelated and have variance ${\mathrm{\sigma }}_c^2$.

By fixing TR and applying a different nominal flip angle for each i, T₁ can be estimated from the resulting sequence of N_i images. As m₀(x) and s(x, c) are individually not of interest here, their product (m(x, c) = m₀(x)s(x, c)) can be treated as a single unknown such that there are only N_c + 1 target quantities in Eq. [1] for each x. At least two unique flip angles (preferably three or more) must be used for these quantities to be estimable. For single-channel VFA–SGPR sequences (N_c = 1), one only has to choose which fitting method to use. For multichannel VFA–SGPR sequences (N_c > 1), however, one has the added task of determining how to apply the selected fitting method to the multichannel image sequence. Standard fitting methods may be: (1) applied independently on each channel image sequence, with a final T₁ estimate being formed by averaging the set of results; (2) applied on a composite image (e.g., root sum-of-squares) sequence; or (3) generalized such that a single T₁ map is jointly estimated using all coil data sets simultaneously.

Generalized T₁ Fitting Strategies

Typically, T₁ fitting of single-channel data is performed either by approximating and solving Eq. [1] as a linear system or via nonlinear least squares (NLLS) regression. In this section, we generalize these two common approaches for multichannel data. Mirroring the approach of Gupta (10) and Fram et al. (11) for the single-channel problem, if noise is ignored, Eq. [1] can be converted into the following pseudo-linear form:

$$\frac{|g(x,c,i)|}{\sin (\widehat{\mathrm{\theta }}(x,i))}\approx \frac{|g(x,c,i)|}{\tan (\widehat{\mathrm{\theta }}(x,i))}{e}^{-\mathrm{TR}/T_1(x)}+|m(x,c)|[1-e^{-\mathrm{TR}/T_1(x)}].$$ [2]

Although the full complex g(·) could be used in Eq. [2], the magnitude signal is typically used in practice out of convenience and to improve numerical stability. Letting Y_x,c and X_x,c be length-N_i vectors defined element-wise as $Y_{x,c}(i)=\frac{|g(x,c,i)|}{\sin (\widehat{\mathrm{\theta }}(x,i))}$ and $X_{x,c}(i)=\frac{|g(x,c,i)|}{\tan (\widehat{\mathrm{\theta }}(x,i))}$, respectively, Eq. [2] can be expressed as Y_x,c ≈ X_x,ca_x + 1b_x,c, where the slope a_x = exp(−TR/T₁(x)) and intercepts b_x,c = |m(x, c)|[1−a_x], and 1 is a length-N_i vector of ones. These variables can be independently estimated at each pixel location x ∈ Ω via ordinary least squares regression, that is,

$$\begin{array}{lll}\left[\begin{array}{c}{\widehat{a}}_x\\ {\widehat{b}}_{x,1}\\ ⋮\\ {\widehat{b}}_{x,N_c}\end{array}\right]& =& \arg \underset{a_x,b_{x,1},\dots ,b_x,N_c}{\min }\left\{\sum _{c=1}^{N_c}{\Vert X_{x,c}{a}_x+\mathbf{1}{b}_{x,c}-Y_{x,c}\Vert }_2^2\right\}\\ & =& {\left[\begin{array}{cccc}{\sum }_{c=1}^{N_c}{X}_{x,c}^{\ast }{X}_{x,c}& X_{x,1}^{\ast }\mathbf{1}& \cdots & X_{x,N_c}^{\ast }\mathbf{1}\\ {\mathbf{1}}^{\ast }{X}_{x,1}& {\mathbf{1}}^{\ast }\mathbf{1}& & \\ ⋮& & \ddots & \\ {\mathbf{1}}^{\ast }{X}_{x,N_c}& & & {\mathbf{1}}^{\ast }\mathbf{1}\end{array}\right]}^{-1}\\ & & \times \left[\begin{array}{c}{\sum }_{c=1}^{N_c}{X}_{x,c}^{\ast }{Y}_{x,c}\\ {\mathbf{1}}^{\ast }{Y}_{x,1}\\ ⋮\\ {\mathbf{1}}^{\ast }{Y}_{x,N_c}\end{array}\right].\end{array}$$ [3]

The (modulated) spin density and T₁ parameter estimates are then distilled as m(x, c) = b̂_x,c/(1 − â_x) and T₁(x) = −TR/ln(â_x), respectively. Because of its simplicity and fast execution, the linearized approximation paradigm has been widely adopted for estimating T₁ from single-channel VFA SPGR sequences. However, in practice, it can exhibit suboptimal performance because: (1) numerical stability is limited as noise is not accounted for (13,18,19); and (2) the estimates of m₀ and T₁ are inherently biased as the target variables are not wholly decoupled (20).

As noted by Wang et al. (13), a more flexible and robust approach to estimate T₁ from VFA–SPGR sequences is via NLLS regression. The NLLS approach treats m₀ and T₁ as independent quantities and is noise aware, and thus tends to be more stable and exhibits less bias than the pseudo-linear approximation approach discussed above. At each pixel x ∈ Ω, the N_c+1 target variables are directly estimated by solving

$$\begin{array}{l}\left[\begin{array}{c}\widehat{m}(x,1)\\ ⋮\\ \widehat{m}(x,N_c)\\ {\widehat{T}}_1(x)\end{array}\right]=\arg \underset{m(x,1),\dots ,m(x,N_c),T_1(x)}{\min }\\ \times \left\{\sum _{c=1}^{N_c}\sum _{i=1}^{N_i}\frac{1}{2{\mathrm{\sigma }}_c^2}{\left|m(x,c)F(x,i,T_1(x))-g(x,c,i)\right|}^2\right\},\hfill \end{array}$$ [4]

where

$$F(x,i,T_1(x))=\frac{\sin (\widehat{\mathrm{\theta }}(x,i))(1-e^{-\mathit{TR}/T_1(x)})}{1-\cos (\widehat{\mathrm{\theta }}(x,i))e^{-\mathit{TR}/T_1(x)})}.$$ [5]

Solutions to this problem are the maximum likelihood estimators for m₀ and T₁. Eq. [4] can be solved using standard nonlinear optimization techniques, including: (1) Levenberg–Marquardt iteration (13,21,22); (2) iteratively reweighted least squares regression (20); and (3) variable projection (7,18,23,24).

Variable projection is particularly appealing for problems in which the target cost functional is quadratic with respect to one or more variables, as it reduces the dimensionality of the optimization problem. This has both quantitative and computational advantages. For the problem inherent to Eq. [4], closed-form expressions for the parameters satisfying the optimality condition, ∇_m̄(x,·) = 0, can be readily defined, that is:

$$m(x,c)=\frac{{\sum }_{i=1}^{N_i}F(x,i,T_1(x))g(x,c,i)}{{\sum }_{i=1}^{N_i}|F(x,i,T_1(x)){|}^2}.$$ [6]

Embedding these expressions into Eq. [4] yields, independently for each x ∈ Ω, the following:

$$[{\widehat{T}}_1(x)]=\arg \underset{T_1(x)}{\min }\left\{\sum _{c=1}^{N_c}\sum _{i=1}^{N_i}\frac{1}{2{\mathrm{\sigma }}_c^2}{\left|\frac{{\sum }_{i\prime =1}^{N_i}F(x,i\prime ,T_1(x))g(x,c,i\prime )}{{\sum }_{i\prime =1}^{N_i}{\left|F(x,i\prime ,T_1(x))\right|}^2}\times F(x,i,T_1(x))-g(x,c,i)\right|}^2\right\}.$$ [7]

One-dimensional optimization problems like Eq. [7] can be simply and efficiently solved using derivative-free methods. As a viable range ([α, β]) for the target variable is known a priori, golden section search (GSS) (25) is particularly attractive as its runtime can be predicted based on desired estimate resolution (tol): $\mathrm{maxIter}=\lceil \ln (\mathit{tol}/(\mathrm{\beta }-\mathrm{\alpha }))/\ln ((\sqrt{5}-1)/2)\rceil$. For example, T₁ can often be assumed to lie between α = 0 ms and β = 10000 ms. If a resolution of tol = 1 ms is deemed sufficient, only maxIter = 20 iterations are required by GSS to perform the estimation. A pictorial example of this fitting procedure is shown in Fig. 1.

FIG. 1.

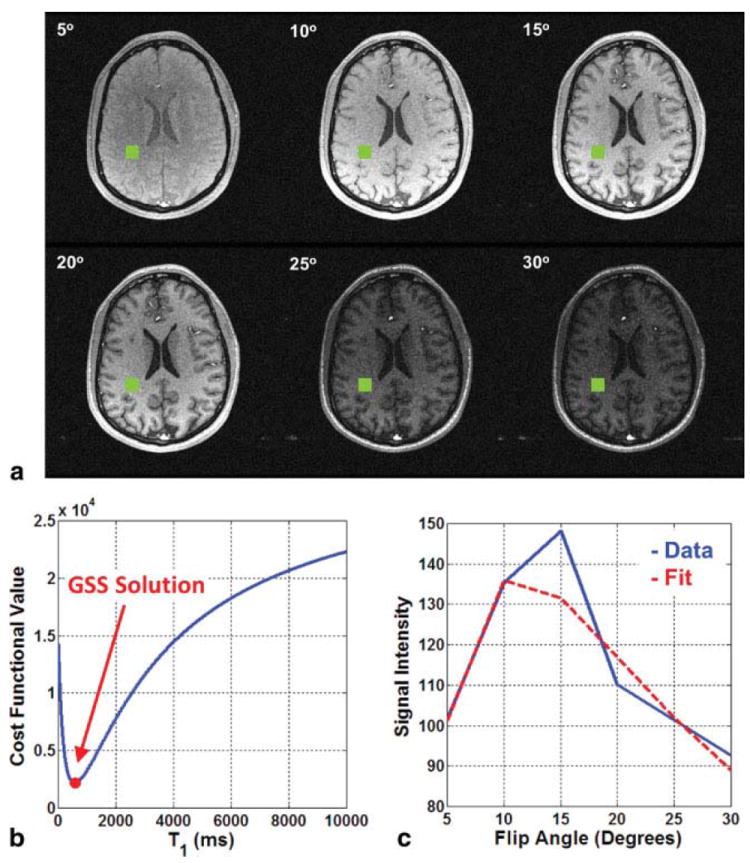
a: The white matter voxel of interest is shown in green on each of the six flip angle images. b: Using the signal from the voxel of interest, the cost functional in Eq. [7] is computed for integer T₁ values between 0 and 10000. GSS easily finds the minimum of this unimodal functional. c: Using the T₁ value estimated by via GSS, the spin density parameter, m₀, is determined and the SPGR signal model in Eq. [1] is (implicitly) fit to the raw data.

Different Ways to Apply a Fitting Strategy to MultiChannel Data

In addition to selecting a fitting strategy (e.g., NLLS), one must also choose how to apply that strategy to multichannel data when estimating T₁ from VFA–SPGR sequences. When directly applied to a multichannel data sequence, both fitting strategies described in the last section correspond to so-called joint estimation, as a single T₁ estimate is directly generated. Joint estimation via NLLS is the most theoretically appealing approach considered in this work, as it corresponds to the maximum likelihood estimator for T₁ in Eq. [1]. It will herein be considered the “gold standard” against which other strategies are compared.

Although attractive, joint estimation can be computationally intensive and so may be impractical in certain clinical situations. Alternatively, multichannel data can be treated as a set of N_c-independent sequences, with a separate fitting being performed on each channel and the N_c results aggregated to yield the final T₁ estimate. If the signal is assumed to be “noise-free,” as in linearized approximation, then uniform averaging of the different channel estimates is warranted. However, for noise-corrupted signals, a weighted average (e.g., by the expected SNR of base signal) of the different channel estimation results may yield better performance than simple uniform averaging. Channel-by-channel estimation may exhibit some computational advantage over joint estimation as it eliminates cross-channel computations; however, it is also (relatively) less statistically efficient than joint estimation as the number of effective variables in the estimation problem is increased from N_c + 1 to 2N_c for each pixel, x. Thus, even an “optimally” weighted aggregate of channel-by-channel will typically not outperform joint estimation.

A third strategy is to perform T₁ estimation on a sequence of composite images, such as those formed by computing the root-sum-of-squares (RSS) across the channel dimension. This type of strategy is commonly applied in practice albeit often implicitly. As the composite image-based approach reduces the dimensionality of the estimation problem, it is computationally very attractive — N_c times less work is needed than for the channel-by-channel strategy. Noise amplification is also mitigated as estimation is ultimately performed on a high SNR signal. However, as composite images typically contain nonadditive, nonzero mean noise, care must be taken to avoid generating heavily biased estimates. From well-known results on Rician statistics (26),

$$\mathrm{E}[|g(x,c,i){|}^2]=|m(x,c)F(x,i,T_1(x)){|}^2+2{\mathrm{\sigma }}_c^2.$$ [8]

Eq. [8] suggests the use of the following “debiased” composition strategy in lieu of standard RSS coil image composition:

$$\begin{array}{ccc}h(x,i)& =& \sqrt{\sum _{c=1}^{N_c}\max ({|g(x,c,i)|}^2-2{\mathrm{\sigma }}_c^2,0)}\\ & \approx & \sqrt{\sum _{c=1}^{N_c}{|m_c(x)|}^2}F(n,i,T_1(x))\hfill \end{array}$$ [9]

(27). h can be treated as a single-channel sequence (N_c = 1) and subsequently processed using the fitting strategies described in the last section. Although composite imagebased strategies are not statistically optimal, they may offer practical advantage if their accuracy is comparable to that of joint NLLS estimation.

METHODS

Data Acquisition

Two volunteers were imaged under an IRB-approved protocol on a 1.5-Tesla system (GE Signa v.14.0, Waukesha, WI) using a standard three-dimensional SPGR sequence (TR/echo time = 15/5 ms, field-of-view = 24 cm, 256×256 matrix, BW = ±31.25 kHz, NEX = 1, 28 1 mm axial slices) and an eight-channel receive-only head coil. Raw k-space data were retained for both studies such that the complete (complex) multichannel image sequence was available for processing. Three different flip angles were used during the first volunteer study (2°, 10°, 25°), and six during the second (5°, 10°, 15°, 20°, 25°, 30°). In both cases, prescan parameters determined for the 25° prescription were used for the acquisition sequences for all other flip angles. B₁ mapping was not performed, and so the nominal and effective flip angles were assumed to be identical. Coil noise statistics were estimated from a small background region of the images. The total imaging time for the volunteer studies were 4.92 and 9.83 min, respectively. We acknowledge that these scan times are longer than typically used in clinical practice; however, we note that use of acceleration strategies (e.g., partial Fourier, parallel imaging) would also require use of a generalized signal model in lieu of the standard SPGR model in Eq. [1], which is beyond the scope of this study.

Data Processing

All T₁ estimation experiments were executed in Matlab (Mathworks, Natick, MA) on a dual six-core (Intel x5670, 2.93 GHz, 12MB cache) machine with 24-GB DDR3 1333 MHz memory. Both the linearized approximation and variable projection-based NLLS fitting strategies described in the Theory section were applied to the multichannel data sequences in the following manner: (1) jointly; (2) channel-by-channel; (3) to an RSS composite image; and (4) to a debiased composite image generated according to Eq. [9]. Correspondingly, eight different T₁ estimates were formed for each volunteer study. As discussed in the Theory section, channel-by-channel and joint linearized approximation were performed on magnitude image data, whereas channel-by-channel and joint NLLS fitting was performed directly on the complex image data. Channel-by-channel linearized approximation results were uniformly averaged, corresponding to the “noise-free” signal assumption of the fitting strategy. For consistency, channel-by-channel NLLS results were also aggregated via uniform averaging. The GSS optimization routine used by NLLS was parameterized as α = 0 ms, β = 10000 ms, and tol = 1 ms for all executions.

RESULTS

Figure 2 shows representative T₁ maps generated of the mid-level brain for each volunteer by the different fitting strategies. Corroborating previous reports (20), linearized approximation exhibits visible upward bias relative to NLLS in brain tissue (not including cerebrospinal fluid, whose low SNR can actually lead to downward bias). The magnitude of T₁ bias also appears to amplify during joint regression, which is undesirable but not unexpected. Noting that bias magnitude exhibits an inverse relationship with SNR (20), we highlight that these trends are especially evident in the results for volunteer #1 (acquired with only three flip angles).

FIG. 2.

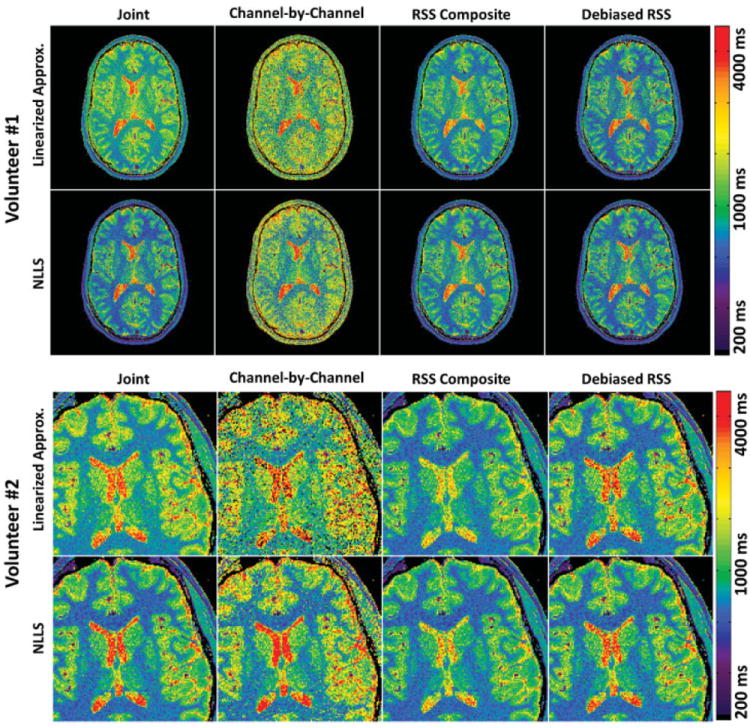
T₁ maps generated for Volunteers #1 and #2 using linearized approximation (top rows) and NLLS regression (bottom rows). Each of the four columns represents a different multichannel handling strategy, specifically joint (1st column), channel-by-channel (2nd column), RSS composite based (3rd column), and debiased RSS composite based (4th column) estimation. Joint NLLS estimation is considered the “gold standard.” All maps were windowed and leveled identically.

To quantitatively characterize the observed trends, eight neuroanatomical regions-of-interest (ROIs) were manually identified for each volunteer study for comparative evaluation. The approximate locations of these ROIs are shown in Fig. 3b. For each T₁ estimation result for a study, and for every ROI, the median was computed as a robust measure of the central tendency (Table 1). These values are largely consistent with the literature (e.g., (28)). Paired comparisons of brain tissue intra-ROI T₁ values were performed between corresponding linearized approximation and NLLS results via the one-sided Wilcoxon sign-rank test (29) (Table 2), under the null hypothesis that, for a particular multichannel handling strategy, linearized approximation estimates smaller T₁ values than NLLS. Evidence in Table 2 suggests that this null hypothesis can be rejected (P < 0.05) in the strong majority of cases (22/24 cases for volunteer #1 and 24/24 cases for volunteer #2). Thus, the relative upward bias of linearized approximation for brain tissues (again, not including cerebrospinal fluid) appears to manifest under any multichannel handling strategy albeit with varying degree.

FIG. 3.

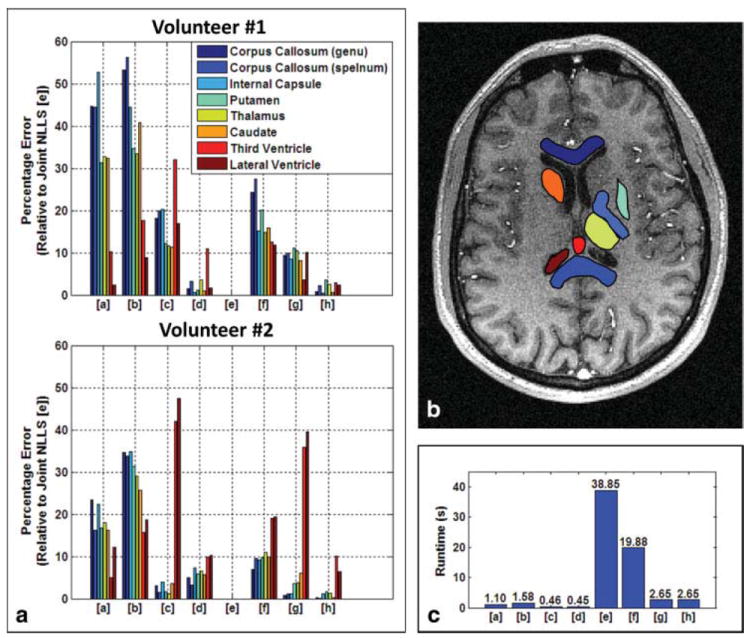
a: Percentage error (relative to joint NLLS) of the various estimation results. For all subfigures, fitting procedures are indexed as linearized approximation [a–d] and NLLS regression [e–h]. Multichannel handling strategies are indexed as joint [a,e], channel-by-channel [b,f], RSS composite based [c,g], and debiased RSS composite based [d,h] estimation. b: Locations of neuroanatomical ROI’s. c: Average runtimes for different fitting and multichannel handling strategies.

Table 1.

Median Observed T₁ relaxation Times for Various Neuroanatomical Regions, as Estimated via Linearized Approximation [a–d] and NLLS Regression [e–h].

	[a]	[b]	[c]	[d]	[e]	[f]	[g]	[h]
Volunteer #1
Corpus callosum (Genu)	1028	1089	840	722	711	884	778	717
Corpus callosum (Splenum)	1056	1142	876	755	731	932	804	747
Internal capsule	1177	1114	927	776	771	888	837	774
Putamen	1441	1477	1231	1109	1097	1317	1220	1136
Thalamus	1565	1574	1317	1221	1179	1354	1303	1210
Caudate	1576	1676	1326	1203	1191	1380	1289	1183
Third ventricle	4311	4596	2657	4339	3908	4395	3766	4021
Lateral ventricle	4632	4933	3761	4603	4528	5066	4072	4421
Volunteer #2
Corpus callosum (Genu)	874	953	730	743	708	757	702	710
Corpus callosum (Splenum)	882	1015	770	784	759	831	751	758
Internal capsule	1003	1106	852	879	820	895	810	830
Putamen	1391	1564	1172	1261	1191	1307	1149	1201
Thalamus	1354	1480	1134	1223	1147	1273	1104	1162
Caudate	1516	1640	1257	1379	1305	1435	1225	1302
Third ventricle	4228	3753	2583	4012	4454	5301	2856	4008
Lateral ventricle	3952	3655	2362	4033	4498	5369	2718	4207

Each table column corresponds to a different multichannel handling strategy, specifically joint [a,e], coil-by-coil [b,f], RSS composite based [c,g], and debiased RSS composite based [d,h] estimation. All times are in ms.

Table 2.

p-values Generated for Brain Tissue ROIs by One-sided Wilcoxon Sign-Rank Test Under Null Hypothesis that, for a Particular Multi-Channel Handling Strategy, Linearized Approximation Estimates Smaller T₁ Values than NLLS.

Volunteer #1	JOINT	COIL-BY-COIL	RSS	DEBIASED RSS
Corpus Callosum (Genu)	<0.0001	<0.0001	<0.0001	0.0280
Corpus Callosum (Splenum)	<0.0001	<0.0001	<0.0001	0.0478
Internal Capsule	<0.0001	<0.0001	<0.0001	0.0108
Putamen	<0.0001	<0.0001	0.0013	0.0303
Thalamus	<0.0001	<0.0001	<0.0001	0.0182
Caudate	<0.0001	<0.0001	0.1457	0.4246
Volunteer #2
Corpus Callosum (Genu)	<0.0001	<0.0001	<0.0001	<0.0001
Corpus Callosum (Splenum)	<0.0001	<0.0001	<0.0001	<0.0001
Internal Capsule	<0.0001	<0.0001	<0.0001	<0.0001
Putamen	<0.0001	<0.0001	<0.0001	<0.0001
Thalamus	<0.0001	<0.0001	<0.0001	<0.0001
Caudate	<0.0001	<0.0001	0.0011	<0.0001

DISCUSSION

In addition to the choice of flip angles and T₁ fitting strategy, how multichannel data is handled also appears to have a substantial impact on estimation performance (refer Table 1). For both linearized approximation and NLLS, joint estimation admits markedly better regional homogeneity than its channel-by-channel analog for both volunteers. This trend is not surprising as the former paradigm contains fewer unknown quantities and is thus (relatively) more statistically efficient. As discussed in the Theory section, channel-by-channel performance could potentially be improved using an SNR-weighted rather than uniform averaging to aggregate the results. For linearized approximation, however, using such a strategy would be inconsistent with the assumption that the base signal is inherently “noise-free,” and so was not considered. A preliminary investigation into the use of (expected) SNR-weighted averaging was performed for the channel-by-channel NLLS results; however, the results (not included here) suggested that such a migration, while improving the results somewhat, would not affect the relative rankings of the tested strategies.

Composite image-based methods also outperform their channel-by-channel analog in terms of signal quality, due to their use of higher SNR base signals. There are, however, noticeable differences between the T₁ maps generated using standard and debiased RSS composite images, which can be attributed to the methods’ use of base signals with differing noise properties. Low SNR regions of single-channel magnitude MR images are well-known to exhibit positive bias (refer Eq. [8]) due to the asymmetry of the corrupting Rician noise distribution. Standard RSS composite images, which are formed by aggregating a set of magnitude images, inherit this bias. As the presumed MR signal model, Eq. [1], is inversely related to T₁, fitting a positively biased signal yields an underestimated T₁ value. However, as demonstrated, the degree of this underestimation can be mitigated by instead using a composition procedure that prospectively accounts for this bias. In low-SNR signal regions, the difference in T₁ values estimated from a standard and debased RSS composite image can be substantial. For example, for volunteer #1, there was ~16% difference in median T₁ value of the anterior corpus callosum (genu) between the standard and debiased RSS linearized approximation results. Similarly, for volunteer #2, there was ~35% difference in median T₁ value of the lateral ventricle between the standard and debiased RSS NLLS results. Despite these improvements, we highlight that some discrepancies still exist between the debiased composite image-based estimates and the joint NLLS results, simply because the latter leverages a more comprehensive signal model.

Theoretically, linearized approximation is invariant to the choice of magnitude or complex data as it assumes that the base signal is “noise-free.” Practically, this choice will cause noise to affect fitting performance differently. Although using linearized approximation on complex data may seem benign, this can lead to numerical instabilities when dividing by the logarithm of the slope regression parameter to determine T₁. Moreover, during joint linearized approximation, the compounding of phase errors in this processing step can yield substantial bias in the final T₁ estimate. Performing linearized approximation on magnitude data mitigates some of these numerical issues, but instead faces the Rician-type bias issues discussed earlier. Nonetheless, preliminary testing suggested that fitting the magnitude signal was more favorable in terms of both numerical stability and performance and, given its general prevalence, was adopted in this work.

Joint NLLS estimation is not only the most statistically attractive approach considered in this work but also the most computationally expensive. Thus, a less expensive paradigm which reasonably mimics joint NLLS performance may be practically advantageous in certain situations. To characterize differences between joint NLLS and the other estimation strategies, absolute relative (i.e., percentage) differences of intra-ROI median values were performed. The results are shown in Figure 3a. Mirroring the visual difference in Figure 2, the strong noise amplification present in the channel-by-channel results makes them not competitive with other strategies. Similarly, joint linearized approximation yields results that are too strongly biased, despite reduced noise compared to the channel-by-channel results. Of the composite image based approaches, NLLS not surprisingly outperforms linearized approximation, and debiased RSS outperforms standard RSS.

Like estimation quality, computational expense also depends on the what T₁ estimation paradigm is used. The eight considered estimation approaches were executed 10 times each for both volunteers. The overall average time for each method is shown in Figure 3c. On inspection, two trends immediately emerge. First, linearized approximation is always faster than NLLS. Joint NLLS estimation is clearly the most intensive approach, requiring ~ 35× more effort than its linearized approximation counterpart. At best, composite image-based NLLS estimation is only ~ 6× slower. Second, composite image-based methods are less computationally expensive than methods that directly fit multichannel data. For NLLS, this difference in computational expense is upward of ~ 14×. Thus, if computational expense precludes use of joint NLLS, using NLLS with the debiased composite image as the base signal may be a practical and effective alternative.

CONCLUSIONS

In this note, we have demonstrated that the performance of VFA–SPGR-based T₁ estimation strongly depends on how multichannel data is handled during processing, and that this aspect should be considered equally important to the selection of a fitting strategy and the number of used flip angles. Our results corroborate previous observations for single channel acquisition (20) that linearized approximation is biased relative to NLLS for brain tissues and suggest that this trend occurs regardless of which multichannel handling strategy is used. We have also shown that linearized approximation (10,11) can be generalized for joint regression, although improved SNR comes at the expense of amplified bias.

Focusing on NLLS-based strategies, joint regression remains the method of choice for estimating T₁ from multi-channel VFA–SPGR data if computational expense is not of concern. Conversely, channel-by-channel strategies are computationally inefficient and poorly performing, and so should not be considered. Composite image-based strategies are computationally attractive; however, care must be taken to mitigate bias that manifests from noise during channel combination. As demonstrated, a strategy which uses NLLS regression and the debiased channel composition strategy proposed in Eq. [9] yields strong categorical emulation of joint NLLS regression albeit in over an order of magnitude less computation time.

The relative performance trends of the methods considered in this work should directly translate for advanced hardware implementations [e.g., GPUs (19)], as well as to variable TR paradigms (18,24) and potentially other quantitative MRI applications where multichannel data handling has historically been a secondary consideration.