Abstract
Particles composed of secondary organic material (SOM) are abundant in the lower troposphere. The viscosity of these particles is a fundamental property that is presently poorly quantified yet required for accurate modeling of their formation, growth, evaporation, and environmental impacts. Using two unique techniques, namely a “bead-mobility” technique and a “poke-flow” technique, in conjunction with simulations of fluid flow, the viscosity of the water-soluble component of SOM produced by α-pinene ozonolysis is quantified for 20- to 50-μm particles at 293–295 K. The viscosity is comparable to that of honey at 90% relative humidity (RH), similar to that of peanut butter at 70% RH, and at least as viscous as bitumen at ≤30% RH, implying that the studied SOM ranges from liquid to semisolid or solid across the range of atmospheric RH. These data combined with simple calculations or previous modeling studies are used to show the following: (i) the growth of SOM by the exchange of organic molecules between gas and particle may be confined to the surface region of the particles for RH ≤ 30%; (ii) at ≤30% RH, the particle-mass concentrations of semivolatile and low-volatility organic compounds may be overpredicted by an order of magnitude if instantaneous equilibrium partitioning is assumed in the bulk of SOM particles; and (iii) the diffusivity of semireactive atmospheric oxidants such as ozone may decrease by two to five orders of magnitude for a drop in RH from 90% to 30%. These findings have possible consequences for predictions of air quality, visibility, and climate.
Keywords: aerosol, physical properties, secondary organic aerosol
Biological sources (e.g., vegetation) and anthropogenic sources (e.g., transportation) emit copious quantities of volatile organic compounds, such as α-pinene and aromatic hydrocarbons, among others (1, 2). In the atmosphere, a complex series of chemical reactions oxidizes these volatile compounds to form semivolatile organic compounds (SVOCs) that condense to the particle phase (1, 2). This secondary organic material (SOM) constituting the particles is estimated to contribute typically 30–70% to the mass concentration of suspended submicron particles in most regions of the atmosphere (1). These particles can influence climate by scattering and absorbing solar radiation (direct climate effect) and by serving as nuclei for cloud formation (indirect climate effect), among other mechanisms (3). They can also influence air quality and health (4–6).
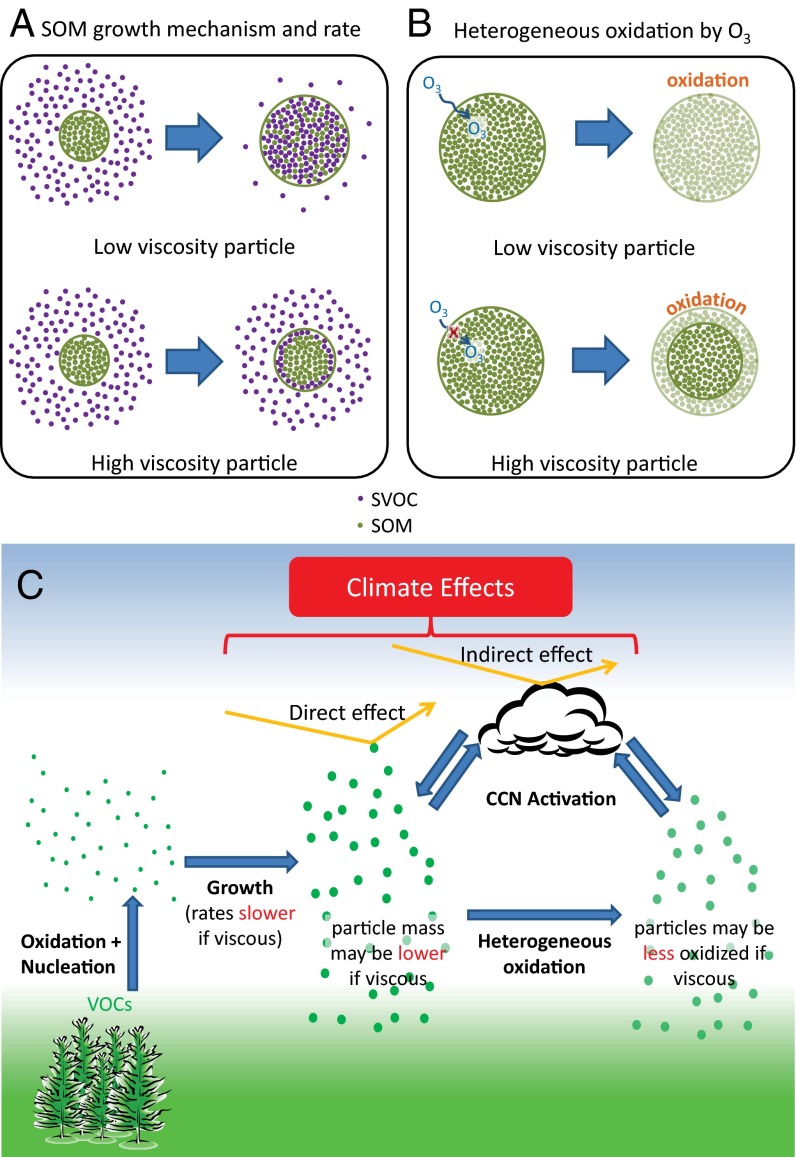
Recently, molecular diffusion within SOM particles has become an area of intense scientific interest. Diffusion rates within particles can influence the mechanism and rates of growth of SOM particles (Fig. 1A) (7, 8) and influence reactions of oxidants within the SOM particles (Fig. 1B) (9). As a result, quantitative modeling of the environmental impacts of SOM particles can depend on molecular diffusion within the particles (see, for example, Fig. 1C). Shiraiwa and Seinfeld (10) have shown that predictions of the mass concentration of SOM particles, a key indicator of air quality, can depend strongly on molecular diffusion rates within particles. Riipinen et al. (8) have demonstrated that predictions of the number concentration and mode diameter of atmospheric particles, which are key parameters for quantitative modeling of the direct and indirect effect of particles on climate, can depend on the mechanism of SOM growth. Shiraiwa et al. (9) have shown that predictions of chemical aging of atmospheric particles by heterogeneous reactions can depend on mass transport rates within the SOM phase. Zelenyuk et al. (11) have established that predictions of the transport of carcinogenic chemicals, such as polycyclic aromatic hydrocarbons (PAHs), to locations far from their source regions can depend on diffusion rates within particles.
Fig. 1.
(A) Effect of particle viscosity on the mechanism of growth of SOM by semivolatile organic compound (SVOC) uptake. (B) Effect of particle viscosity on heterogeneous oxidation by ozone. (C) Climate effects of particles and implications of high particle viscosities on particle growth rates, particle mass, and heterogeneous oxidation by 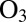 . The implications of particle viscosity on growth and heterogeneous oxidation in A–C assume a monodisperse particle population.
. The implications of particle viscosity on growth and heterogeneous oxidation in A–C assume a monodisperse particle population.
In many large-scale modeling studies, it is often assumed that equilibrium is rapidly achieved between gas-phase organic compounds and the bulk of SOM particles (2, 12–14). This assumption implies that diffusion within the particles is fast compared with accommodation (10). More recently, strong evidence emerged that some SOM particles, including but not limited to SOM from α-pinene ozonolysis, can behave as semisolids or solids under some conditions, such as low relative humidity (7, 15–22). At the present time, however, estimates available in the literature for molecular diffusivity inside SOM are limited to dry conditions [relative humidity (RH) 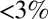 ] (7, 15) whereas atmospheric conditions may cover the full range of RH, with typical values ranging from ∼20% to 100% in the planetary boundary layer (23–25). As a result, diffusion rates within SOM particles under typical atmospheric conditions are uncertain, and this uncertainty implies concomitant uncertainty for predicting the impacts of SOM particles on air quality, visibility, and climate (26).
] (7, 15) whereas atmospheric conditions may cover the full range of RH, with typical values ranging from ∼20% to 100% in the planetary boundary layer (23–25). As a result, diffusion rates within SOM particles under typical atmospheric conditions are uncertain, and this uncertainty implies concomitant uncertainty for predicting the impacts of SOM particles on air quality, visibility, and climate (26).
Our strategy for quantification of molecular diffusivity is to make experimental measurements of viscosity, η. Viscosity and molecular diffusion rates are related by the Stokes–Einstein equation in the case of self-diffusion (i.e., similarly sized molecules) or by other approaches such as percolation theory for the diffusion of a small molecule in a host matrix of large molecules (26, 27). As is the case for molecular diffusivity, quantitative determination of SOM viscosity is lacking for the range of relative humidity typical of the atmosphere.
Herein, we use two uniquely developed techniques to measure at room temperature (293–295 K) the RH-dependent viscosity of the water-soluble component of SOM particles produced by α-pinene ozonolysis, a major source of SOM particles in the atmosphere, especially over boreal forests (28). The water-soluble component makes up the major fraction of SOM particles from α-pinene ozonolysis (SI Materials and Methods). These unique techniques for viscosity measurements were needed because conventional viscometers are not able to accommodate the small sample volumes associated with laboratory or atmospheric sampling of SOM particles (typically on the order of 1 μL). Moreover, microviscometers that can accommodate small sample sizes are often limited to measurements of low viscosities (<0.1 Pa·s) (29–32), whereas SOM is anticipated to have considerably higher viscosity, at least at low RH. These techniques may also find broader future use in other disciplines that require viscosity measurements of small sample volumes, e.g., due to cost or availability such as biological samples.
Results
The first technique used to quantify viscosity was based on the mobility of beads inserted inside SOM particles (i.e., bead-mobility technique) (33). SOM from the dark ozonolysis of α-pinene was produced in two continuous-flow environmental chambers and collected on filters. The water-soluble component of this material was extracted using high-purity water, and the water extract was nebulized to generate supermicron particles deposited on a hydrophobic glass slide. A dilute suspension of small insoluble beads (1 μm in diameter) was sprayed over the SOM particles, and these beads settled into the larger SOM particles. The slide was mounted in an RH-controlled flow cell that was held at room temperature (293–295 K), and a flow of gas (nitrogen and water vapor) was introduced over the SOM particles, producing a shear stress on the particle surface. This shear stress generated viscosity-dependent rates of internal circulation, and this circulation was visualized by movement of the beads in the particle matrix (Fig. S1 and Movie S1). After equilibration at a known RH, images of the supermicron (30–50 μm diameter) particles were recorded using an optical microscope and subsequently analyzed to calculate the average bead speed within the particle matrix. The speed was converted to viscosity by a calibration curve (SI Materials and Methods and Fig. S2) (33).
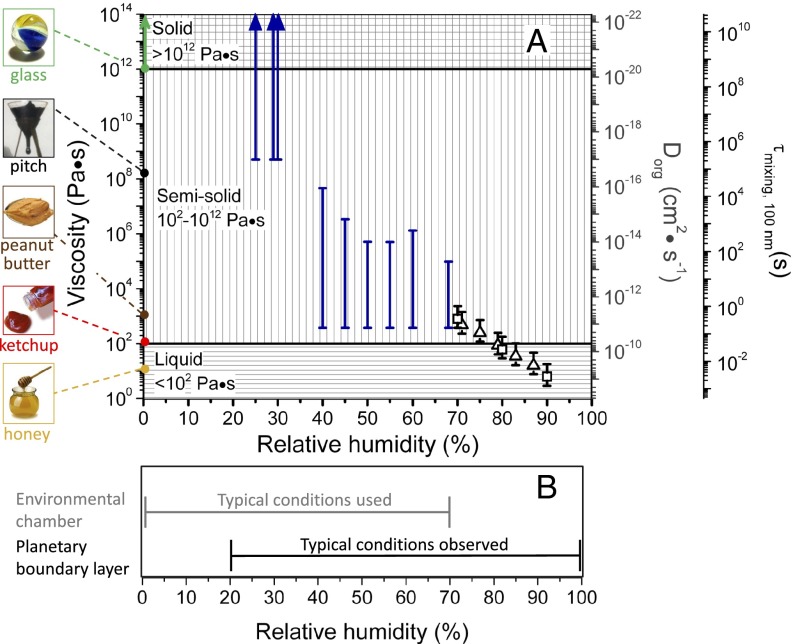
The average bead speeds and associated viscosities determined between 70% and 90% RH are listed in Table 1. The viscosities are also shown in Fig. 2. At 70% RH the viscosity (±95% prediction limits) of the SOM was 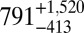 Pa·s, comparable to that of peanut butter. At 90% RH the viscosity of the SOM was
Pa·s, comparable to that of peanut butter. At 90% RH the viscosity of the SOM was 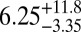 Pa·s, comparable to that of honey. Bead speeds were not determined for RH < 70% because the rate of circulation became too slow to readily observe.
Pa·s, comparable to that of honey. Bead speeds were not determined for RH < 70% because the rate of circulation became too slow to readily observe.
Table 1.
Mean bead speeds in water-soluble SOM from α-pinene ozonolysis and corresponding viscosities
| Chamber sample | RH, % | Mean bead speed, μm/ms | Viscosity, ± 95% prediction limits, Pa·s |
| HEC* | 90 | 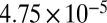 |
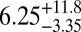 |
| 80 | 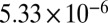 |
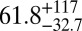 |
|
| 70 | 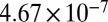 |
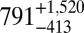 |
|
| PNNL† | 87 | 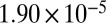 |
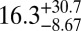 |
| 83 | 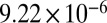 |
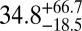 |
|
| 79 | 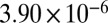 |
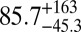 |
|
| 75 | 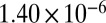 |
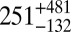 |
|
| 71 | 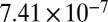 |
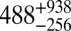 |
HEC refers to samples collected on quartz fiber filters from the Harvard Environmental Chamber.
PNNL refers to samples collected on Teflon filters from the Pacific Northwest National Laboratory Continuous-Flow Environmental Chamber.
Fig. 2.
(A) Summary plot of the SOM viscosities determined by a combination of the “bead-mobility” [black open squares and triangles for Harvard Environmental Chamber (HEC) and PNNL samples, respectively, where the black bars represent the 95% prediction intervals] and “poke-flow” experiments (where the blue bars represent the bounds of the viscosities). HEC refers to samples collected on quartz fiber filters from the Harvard Environmental Chamber. PNNL refers to samples collected on Teflon filters from the Pacific Northwest National Laboratory Continuous-Flow Environmental Chamber. Various common substances have been placed alongside the diagram, along with their approximate viscosities at room temperature, to provide points of reference following the idea of Koop et al. (26). The secondary y axes show (i) diffusion coefficients of organic molecules (Dorg) in SOM calculated using the Stokes–Einstein relation and (ii) mixing times 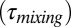 of the particles due to bulk diffusion in 100-nm particles of the same viscosity (main text). The image of the pitch is a detail of an image from the pitch drop experiment (image courtesy of Wikimedia Commons, GNU Free Documentation License, University of Queensland, Australia, John Mainstone). (B) Typical relative humidities observed in the planetary boundary layer (23–25) and environmental chambers (52, 53).
of the particles due to bulk diffusion in 100-nm particles of the same viscosity (main text). The image of the pitch is a detail of an image from the pitch drop experiment (image courtesy of Wikimedia Commons, GNU Free Documentation License, University of Queensland, Australia, John Mainstone). (B) Typical relative humidities observed in the planetary boundary layer (23–25) and environmental chambers (52, 53).
The second technique used to quantify viscosity was a poke-flow approach. The qualitative method of poking a particle to determine the particle phase (i.e., solid/semisolid vs. liquid) was introduced by Murray et al. (34). Herein, this approach was expanded upon by quantifying flow rates after poking, and this information was used in conjunction with simulations to estimate upper limits to the viscosity for 40–70% RH and lower limits for 25–30% RH.
Supermicron SOM particles were deposited on hydrophobic glass slides as described above. In an RH-controlled flow cell (Fig. S3), particles were allowed to equilibrate. The resulting particles were 20–50 μm in diameter. These SOM particles were deformed to a nonequilibrium shape by poking the particles with a sharp needle. In experiments of RH ≥ 40%, the needle penetrated the particle, resulting in a half-torus shape being generated after the needle was retracted (e.g., Fig. 3 A–C). The material flowed at an observable rate to restore a spherical cap, minimizing the surface energy of the system (e.g., Fig. 3 A–C and Movie S2). The experimental flow time, 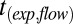 , required for the inner diameter of the half-torus to decrease to 50% of its initial diameter was determined by analysis of a time series of images. The flow time increased from ∼10 s at 70% RH to 4,000 s at 40% RH (Table 2).
, required for the inner diameter of the half-torus to decrease to 50% of its initial diameter was determined by analysis of a time series of images. The flow time increased from ∼10 s at 70% RH to 4,000 s at 40% RH (Table 2).
Fig. 3.
Deformation and recovery across time of poked SOM particles. Before poking (prepoke), the particle morphology can be approximately described as a spherical cap. At higher RH (40–70%) (A–C), geometries approximately described as half-torus are formed, and flow occurs. By comparison, for low RH (≤30%) (D) particles shatter and do not flow over a period of 8 h. The ring structures observed in the first and last columns are an optical effect that arises from hemispherical diffraction.
Table 2.
Results from poke-flow experiments
| Chamber sample | RH, % |
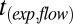 , s* , s*
|
Lower limit of viscosity, Pa·s† | Upper limit of viscosity, Pa·s‡ |
| HEC | 70 | 50.9 | 378 | 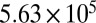 |
| PNNL | 68 | 8.98 | 378 | 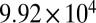 |
| 60 | 116.5 | 378 | 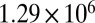 |
|
| 55 | 46.0 | 378 | 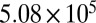 |
|
| 50 | 47.0 | 378 | 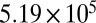 |
|
| 45 | 305 | 378 | 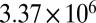 |
|
| 40 | 4,090 | 378 | 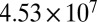 |
The values of 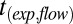 can vary between experiments but the slowest observed flows are reported here to calculate an upper limit to the viscosity.
can vary between experiments but the slowest observed flows are reported here to calculate an upper limit to the viscosity.
A lower limit (378 Pa·s) was established for 40–70% RH on the basis of the lower 95% prediction limit from the bead-mobility value at 70% RH.
The upper limits to the viscosities were calculated using 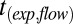 , and the calibration curve shown in Fig. S5.
, and the calibration curve shown in Fig. S5.
Simulations were carried out using the software package COMSOL Multiphysics (SI Materials and Methods) for a particle of half-torus geometry having similar physical dimensions to those of the experimental observations (Fig. S4). Shown in Movie S3 are examples of simulations for a viscosity of 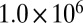 Pa·s. Flow occurred in the simulations in a way that minimized the total surface energy. Modeled flow times,
Pa·s. Flow occurred in the simulations in a way that minimized the total surface energy. Modeled flow times, 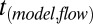 , required for the inner diameter of the torus to decrease to 50% of its initial diameter were determined from the simulations as a function of viscosity, η (Fig. S5). The experimental flow times,
, required for the inner diameter of the torus to decrease to 50% of its initial diameter were determined from the simulations as a function of viscosity, η (Fig. S5). The experimental flow times, 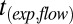 , were converted to viscosities using the function from the modeled viscosity-dependent flow times,
, were converted to viscosities using the function from the modeled viscosity-dependent flow times, 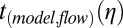 . Because of assumptions used in the simulations, the viscosities determined for 40–70% RH were upper limits (SI Materials and Methods).
. Because of assumptions used in the simulations, the viscosities determined for 40–70% RH were upper limits (SI Materials and Methods).
A lower limit (378 Pa·s) was also established for 40–70% RH on the basis of the lower 95% prediction limit from the bead-mobility value at 70% RH. The upper limits (based on the poke-flow technique) and lower limits (based on the bead-mobility technique) to the viscosities for 40–70% RH are listed in Table 2 and plotted in Fig. 2A. At 40% RH, the limits range from 378 Pa·s to 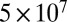 Pa·s, i.e., from approximately the viscosity of peanut butter to that of pitch (35).
Pa·s, i.e., from approximately the viscosity of peanut butter to that of pitch (35).
For RH values of 25–30%, the particles shattered when poked with a needle. Moreover, restorative flow did not occur, at least for the experimental timescale (8–10 h) (e.g., Fig. 3D). The fragments had sharp well-defined edges, and no smoothing of the edges was observed over the course of the experiments (Movie S4). In this case, modeling of the flow established a lower limit to the viscosity. Simulations were initialized as a quarter-sphere having one flat face in contact with a substrate (Fig. S4). In a set of stepwise simulations, the viscosity was decreased until the maximum displacement at the corners of the quarter-sphere was 0.5 μm in 8 h, establishing a lower limit for viscosity of 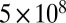 Pa·s (SI Materials and Methods). Images of simulations for this viscosity are shown in Movie S5. This lower limit is included in Fig. 2A, with a value comparable to that of pitch (35).
Pa·s (SI Materials and Methods). Images of simulations for this viscosity are shown in Movie S5. This lower limit is included in Fig. 2A, with a value comparable to that of pitch (35).
Discussion
Amorphous solids have viscosities greater than 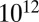 Pa·s, semisolids such as gels or ultraviscous liquids have viscosities between
Pa·s, semisolids such as gels or ultraviscous liquids have viscosities between 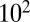 and
and 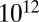 Pa·s, and liquids have viscosities less than or equal to
Pa·s, and liquids have viscosities less than or equal to 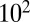 Pa·s (9, 26). These phases are represented by different patterns in Fig. 2, together with the RH-dependent viscosities. The viscosities of the studied SOM correspond to liquid for RH ≥ 80%, a semisolid for 40% ≤ RH < 80%, and a semisolid or solid for RH ≤ 30%. These findings are in agreement with the results of other recent studies suggesting that certain types of SOM do not behave as liquids under some conditions, such as low relative humidity (7, 15–21).
Pa·s (9, 26). These phases are represented by different patterns in Fig. 2, together with the RH-dependent viscosities. The viscosities of the studied SOM correspond to liquid for RH ≥ 80%, a semisolid for 40% ≤ RH < 80%, and a semisolid or solid for RH ≤ 30%. These findings are in agreement with the results of other recent studies suggesting that certain types of SOM do not behave as liquids under some conditions, such as low relative humidity (7, 15–21).
The relationship between RH and viscosity in Fig. 2A can be rationalized by considering the hygroscopic nature of the studied SOM. SOM from α-pinene ozonolysis is known to be hygroscopic, meaning the water content of the particles will increase as the RH increases (36–39). As the particles uptake water, the viscosity of the mixture is thus expected to decrease, because the viscosity of pure water is low (1.002 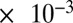 Pa·s at 293 K) (40). This phenomenon may be described, at least to a first-order approximation, by simple mixing rules (SI Materials and Methods). The apparent step in viscosity between 30% and 40% RH may be due to a phase transition, such as the formation of a glass or gel, or may be due to nonideal interactions in the complex mixture (SI Materials and Methods).
Pa·s at 293 K) (40). This phenomenon may be described, at least to a first-order approximation, by simple mixing rules (SI Materials and Methods). The apparent step in viscosity between 30% and 40% RH may be due to a phase transition, such as the formation of a glass or gel, or may be due to nonideal interactions in the complex mixture (SI Materials and Methods).
Using the viscosities determined herein and an estimated hydrodynamic radius, we calculated the corresponding Stokes–Einstein-equivalent diffusion coefficients of organic molecules in SOM, 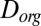 . These values correspond to the right-hand axis of Fig. 2A. The hydrodynamic radius was approximated as the molecular radius of 0.38 nm, given a molecular weight of 175 g·mol−1 (41), a density of 1.3 g·cm−3 (42–44), and molecular spherical symmetry. The obtained
. These values correspond to the right-hand axis of Fig. 2A. The hydrodynamic radius was approximated as the molecular radius of 0.38 nm, given a molecular weight of 175 g·mol−1 (41), a density of 1.3 g·cm−3 (42–44), and molecular spherical symmetry. The obtained 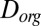 values ranged from
values ranged from 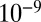 to
to 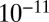 cm2·s−1 between 90% and 70% RH, from
cm2·s−1 between 90% and 70% RH, from 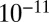 to
to 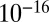 cm2·s−1 between 70% and 40% RH, and to
cm2·s−1 between 70% and 40% RH, and to 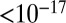 cm2·s−1 for RH ≤ 30%. Three studies have estimated the diffusivity of organic compounds within SOM. Two of these studies, one looking at partitioning of organic nitrates into SOM particles (7) and the other looking at the evolution of the chemical composition of SOM particles after they pass through a thermodenuder (15), have estimated an upper bound of
cm2·s−1 for RH ≤ 30%. Three studies have estimated the diffusivity of organic compounds within SOM. Two of these studies, one looking at partitioning of organic nitrates into SOM particles (7) and the other looking at the evolution of the chemical composition of SOM particles after they pass through a thermodenuder (15), have estimated an upper bound of 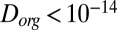 cm2·s−1 for the diffusion coefficient of organic molecules in SOM produced by α-pinene ozonolysis under dry conditions (
cm2·s−1 for the diffusion coefficient of organic molecules in SOM produced by α-pinene ozonolysis under dry conditions (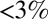 RH). These results are consistent with the results reported herein for RH ≤ 30% (
RH). These results are consistent with the results reported herein for RH ≤ 30% (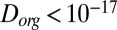 cm2·s−1). The third study (22) quantified the diffusivity of pyrene in SOM under low RH conditions to be
cm2·s−1). The third study (22) quantified the diffusivity of pyrene in SOM under low RH conditions to be 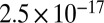 cm2·s−1, similar to, but slightly higher than, the diffusion coefficient measured herein for the water-soluble component of α-pinene at ≤30% RH (
cm2·s−1, similar to, but slightly higher than, the diffusion coefficient measured herein for the water-soluble component of α-pinene at ≤30% RH (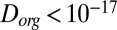 cm2·s−1). The small discrepancy is largely attributed to the hydrodynamic radius of pyrene used in the study by Abramson et al. (22) compared with the hydrodynamic radius of SOM material used to calculate molecular diffusion coefficients from our viscosity data.
cm2·s−1). The small discrepancy is largely attributed to the hydrodynamic radius of pyrene used in the study by Abramson et al. (22) compared with the hydrodynamic radius of SOM material used to calculate molecular diffusion coefficients from our viscosity data.
Detailed modeling studies are required to fully explore the implications for particle viscosity. Here we use the presented viscosity data together with previous modeling studies or simple calculations to provide an initial assessment of the effect particle viscosity on (i) the mechanism of growth of SOM particles, (ii) predictions of particle mass, and (iii) rates of reactions in SOM particles.
Currently most models used for predicting the effect of SOM particles on air quality and climate assume that growth occurs by instantaneous equilibrium partitioning of SVOCs into the bulk of the SOM particles (Fig. 1A, Upper). For this mechanism to be accurate the mixing time of SVOCs within the particles must be short compared with the timescale for particle growth. The mixing times, 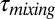 , by diffusion of large organic molecules within an SOM particle can be estimated from the viscosity data and the Stokes–Einstein relation (45),
, by diffusion of large organic molecules within an SOM particle can be estimated from the viscosity data and the Stokes–Einstein relation (45),
 |
in which d is the particle diameter, r is the hydrodynamic radius of a representative molecule of SOM within the SOM bulk matrix, k is Boltzmann’s constant, and T is temperature. After the mixing time, the concentration of the representative molecule anywhere in the particles deviates by less than 1/e from the initial disequilibrium concentration (i.e., a homogenization process). It should be noted that Eq. 1 may be inaccurate near the glass transition temperature/relative humidity due to the possible breakdown of the Stokes–Einstein relation at these viscosities.
Shown in Fig. 2A (right-hand y axis) are mixing times within 100-nm particles, calculated with Eq. 1, the new viscosity data, and assuming a hydrodynamic radius of 0.38 nm. For an RH of 70–90%, the mixing times are 0.01–1 s. In this case instantaneous equilibrium partitioning within the bulk of the SOM particles is likely a valid description of SOM growth (Fig. 1A, Upper). By comparison, the mixing times exceed 2.5 d for RH ≤ 30%. At these relative humidities, gas-particle partitioning of large organic molecules such as pinonaldehyde (the most abundant product of α-pinene ozonolysis) may be effectively confined to the surface of the particle (Fig. 1A, Lower). Hence, the mechanism of growth may not occur by instantaneous equilibrium partitioning within the particle bulk. This is consistent with the conclusions of other studies of α-pinene SOM studied under dry conditions [e.g., Perraud et al. (7) and references therein]. The mechanism of growth may have important consequences for the particle size distribution (8), which may in turn affect the scattering and absorption of solar radiation and the ability of particles to act as nuclei for cloud condensation (3).
At ≤30% RH, because the viscosity of the particles may allow partitioning of SVOCs only within the top few molecular layers of the particle, the particles will take up fewer SVOCs compared with low-viscosity particles where instantaneous equilibrium partitioning within the bulk of SOM particles may occur (Fig. 1A). As a result, models that assume equilibrium partitioning at ≤30% RH may overpredict SOM particle mass and underpredict gas-phase concentrations of SVOCs. Recently Shiraiwa and Seinfeld (10) showed that when the viscosity of the particle is 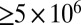 Pa·s, the particle-phase mass concentrations of semivolatile and low-volatility organic compounds may be overestimated by at least an order of magnitude compared with the assumption of instantaneous equilibrium partitioning within the bulk. Considering the new viscosity data and the modeling results from Shiraiwa and Seinfeld (10), we conclude that at ≤30% RH, the particle-mass concentrations of SVOCs and low-volatility organic compounds may be overpredicted by an order of magnitude or more with implications for predictions of air quality and visibility.
Pa·s, the particle-phase mass concentrations of semivolatile and low-volatility organic compounds may be overestimated by at least an order of magnitude compared with the assumption of instantaneous equilibrium partitioning within the bulk. Considering the new viscosity data and the modeling results from Shiraiwa and Seinfeld (10), we conclude that at ≤30% RH, the particle-mass concentrations of SVOCs and low-volatility organic compounds may be overpredicted by an order of magnitude or more with implications for predictions of air quality and visibility.
Reactions between atmospheric oxidants, such as 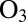 , and particle-phase organic molecules can lead to chemical aging of SOM particles, with possible implications for particle hygroscopicity, optical properties, and toxicity (46, 47). The rates of these aging reactions may depend on the diffusion coefficients of the oxidants,
, and particle-phase organic molecules can lead to chemical aging of SOM particles, with possible implications for particle hygroscopicity, optical properties, and toxicity (46, 47). The rates of these aging reactions may depend on the diffusion coefficients of the oxidants, 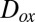 , within the SOM (9, 48, 49). The rates can also depend on the diffusion coefficients of the organic molecules,
, within the SOM (9, 48, 49). The rates can also depend on the diffusion coefficients of the organic molecules, 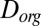 , in the case that the diffusion rates of the organic molecules are slow (9, 49). On the basis of our viscosity data and the Stokes–Einstein equation,
, in the case that the diffusion rates of the organic molecules are slow (9, 49). On the basis of our viscosity data and the Stokes–Einstein equation, 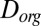 decreases by more than eight orders of magnitude for a drop in RH from 90% to 30%. In organic matrices
decreases by more than eight orders of magnitude for a drop in RH from 90% to 30%. In organic matrices 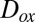 is estimated on the basis of previous measurements of the mobility of small molecules in different matrices to be
is estimated on the basis of previous measurements of the mobility of small molecules in different matrices to be 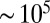 Pa·s for a liquid,
Pa·s for a liquid, 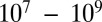 Pa·s for a semisolid, and
Pa·s for a semisolid, and 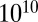 Pa·s for a solid [Shiraiwa et al. (9) and references therein]. Based on these estimates and the phase information elucidated above,
Pa·s for a solid [Shiraiwa et al. (9) and references therein]. Based on these estimates and the phase information elucidated above, 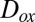 is expected to decrease by at least two to five orders of magnitude for a change in RH from 90% to ≤30% RH as the particles transition from liquid to semisolid/solid. These changes in diffusion coefficients imply that the rates of chemical aging of SOM particles can depend strongly on RH, with a decrease in rates expected with a decrease in RH. In support of these implications, a recent study showed that the reaction rate of
is expected to decrease by at least two to five orders of magnitude for a change in RH from 90% to ≤30% RH as the particles transition from liquid to semisolid/solid. These changes in diffusion coefficients imply that the rates of chemical aging of SOM particles can depend strongly on RH, with a decrease in rates expected with a decrease in RH. In support of these implications, a recent study showed that the reaction rate of 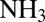 with α-pinene SOM particles decreases significantly for a drop in RH from 95% to 5% (20).
with α-pinene SOM particles decreases significantly for a drop in RH from 95% to 5% (20).
Applying the viscosity measurements from the present study to α-pinene SOM in the atmosphere or environmental chambers is subject to several caveats. First, the study focused on the water-soluble component of SOM. For α-pinene SOM, however, the water-soluble material constitutes the major mass fraction of SOM (SI Materials and Methods). Second, collection of SOM from environmental chambers can be subject to both positive and negative sampling artifacts. Positive artifacts occur due to the adsorption of semivolatile organic material on the filters and are expected to be much less with Teflon filters than with quartz fiber filters (50). Because we obtained the same viscosity results within the uncertainty of the measurements using both Teflon filters and quartz filters (Tables 1 and 2 and Fig. 2), positive artifacts seem unimportant in our experiments. Negative artifacts can include the partial evaporation of semivolatile SOM. This process cannot be ruled for our experiments. As a result the material studied here may be the less volatile component of the water-soluble secondary organic material. These caveats notwithstanding, the results reported herein provide the best estimates of α-pinene SOM viscosities over a wide range of atmospherically relevant relative humidities. Information concerning viscosity and ultimately diffusion coefficients is needed for the accurate modeling of heterogeneous chemistry as well as particle growth and evaporation.
Materials and Methods
A brief description of the experimental procedures is provided below and further details are located SI Materials and Methods.
Production of Secondary Organic Material.
Secondary organic material from the dark ozonolysis of α-pinene was formed by homogeneous nucleation in continuous-flow environmental chambers at Harvard University and Pacific Northwest National Laboratory (PNNL). The setup and experimental conditions were similar to those used by Shilling et al. (51). The α-pinene [80–100 parts per billion by volume (ppbv)], ozone (300 ppbv), and 2-butanol (used as an OH scavenger) were introduced continuously to the chambers in a total flow of 20–25 standard liters per minute (sLpm). The temperature and relative humidity inside the chambers were maintained at 298 K and <5%, respectively. The secondary organic material was collected at the outlet of the Harvard University environmental chamber on a quartz fiber filter (Whatman; 1851-047) and at the outlet of the PNNL chamber on a Teflon filter (Pall; R2PL037). During collection the composition of the SOM was monitored continuously and found to be constant. The collection time for sampling was 48 h at a flow rate of 8.0 sLpm. After collection, filters were stored at 263 K under dry conditions. After extraction, solutions were used within 14 d. The extracted solution was stored at 278 K when not in use. Viscosities measured immediately after filter extraction and 14 d after filter extraction were the same within experimental uncertainty.
Bead-Mobility Technique.
The bead mobility technique has been described in detail recently by Renbaum-Wolff et al. (33). Water-soluble species were extracted from the filters through the addition of 20 mL of ultrapure Millipore water (18.2 MΩ·cm). This solution was nebulized (Meinhard; model TR-30-A1) onto a hydrophobic glass slide or a Teflon slide until large droplets were generated on the slide surface. Next, a dilute aqueous suspension of 1 μm hydrophilic melamine beads [actual diameter 930 ± 50 nm (Sigma Aldrich; no. 86296)] was nebulized over the slide containing the large droplets, resulting in beads being incorporated into the bulk of the particles. Melamine beads were chosen as they are prepared by the manufacturer without the use of surfactants and are not susceptible to swelling or aggregation in solution. The slide containing the large droplets with bead inclusions was then placed in a flow cell with relative humidity control. The flow cell has been described in detail previously (33). A flow of gas was introduced over the particles (linear flow velocity of 100 cm·s−1), producing a shear stress on the particle surface and thereby internal circulations within the particle. These circulations, which carried the beads, were quantified by analysis of a time series of 50–100 images recorded by optical microscopy (Zeiss Axio Observer).
The relative humidity inside the cell was controlled by passing the flow gas 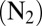 through a water bubbler located in a controlled-temperature bath. The dew point temperature was measured after the flow cell with a hygrometer (General Eastern; Model 1311DR). The temperature of the flow cell was measured using a thermocouple probe. The hygrometer was calibrated at the beginning of each day, using the deliquescence of ammonium sulfate particles.
through a water bubbler located in a controlled-temperature bath. The dew point temperature was measured after the flow cell with a hygrometer (General Eastern; Model 1311DR). The temperature of the flow cell was measured using a thermocouple probe. The hygrometer was calibrated at the beginning of each day, using the deliquescence of ammonium sulfate particles.
At the initiation of the bead mobility experiments, the RH was set at 90% and the particles were allowed to equilibrate for 30 min. The size of these hydrated particles varied between 30 and 50 μm in lateral diameter. After equilibration, the RH was decreased (<0.5% RH·min−1) to the experimental value, at which point the RH was held constant for 20 min to allow sufficient time for the particles to equilibrate with the water vapor. The lowest relative humidity studied was 70% RH for the bead-mobility experiments. Below this RH, the bead speed became too slow to quantify. See SI Materials and Methods for further information.
Poke-Flow Technique.
The poke-flow technique is an extension of the technique used by Murray et al. (34), who used a flat-ended metal rod to probe the physical state of cold droplets of aqueous iodic acid. The current experimental approach is based on poking particles with a sharp needle to generate a nonequilibrium state. After poking the particle, the material flows, with the driving force related to the surface energy of the system. From the experiments we determine flow times, which are then used to determine viscosities.
The same filter extract solutions as used in the bead-mobility technique were used to generate particles on hydrophobic glass slides, as described above. For the poke-flow experiments, the particle diameters ranged from 20 to 50 μm. The slides supporting the particles were placed in a flow cell similar to the one described above except it had a small hole in the top through which a needle could be inserted (Fig. S3).
After the equilibration period (see SI Materials and Methods for further information on equilibration times), the particles were poked by a sterilized needle (Becton-Dickinson; product no. 305888) that was mounted on a micromanipulator (Narishige; model MO-202U). The poking and subsequent behavior of the particles were observed by reflectance optical microscopy (Zeiss Axio Observer). The particles were monitored for up to 8 h after poking. From the images, the times required for the inner diameter of the half-torus geometry to decrease to 50% of its original size were determined, which we refer to as the experimental flow time, 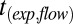 . These flow times were then compared with simulations to determine limit values for viscosity (SI Materials and Methods).
. These flow times were then compared with simulations to determine limit values for viscosity (SI Materials and Methods).
Simulations of Material Flow.
COMSOL Multiphysics, which is a finite-element analysis software package, was used to simulate fluid flow in the poke-flow experiments. Details are given in SI Materials and Methods.
Supplementary Material
Acknowledgments
We thank Dan Bizzotto for helpful advice on interpreting the experimental results and Neil Donahue for useful discussions. We also acknowledge the Laboratory for Advanced Spectroscopy and Imaging Research facility at University of British Columbia for providing the microscope used in these experiments. This work was funded by the Natural Sciences and Engineering Research Council of Canada; the US Department of Energy, Grant DE-FG02-08ER64529; the European Research Council, Grant FP7, 240449 ICE; and the Pacific Northwest National Laboratory (PNNL) Aerosol Climate Initiative. PNNL is operated for the US Department of Energy by Battelle Memorial Institute under Contract DE-AC05-76RL01830.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1219548110/-/DCSupplemental.
References
- 1.Kanakidou M, et al. Organic aerosol and global climate modelling: A review. Atmos Chem Phys. 2005;5:1053–1123. [Google Scholar]
- 2.Hallquist M, et al. The formation, properties and impact of secondary organic aerosol: Current and emerging issues. Atmos Chem Phys. 2009;9:5155–5236. [Google Scholar]
- 3.Solomon S, et al., editors. IPCC Fourth Assessment Report: Climate Change 2007: The Physical Science Basis: Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge, UK: Cambridge Univ Press; 2007. [Google Scholar]
- 4.US Environmental Protection Agency 2008. US Clean Air Act (and subsequent amendments/rulings). Available at www.gpo.gov/fdsys/pkg/USCODE-2008-title42/pdf/USCODE-2008-title42-chap85.pdf. Accessed March 18, 2013. [PubMed]
- 5.Baltensperger U, et al. Combined determination of the chemical composition and of health effects of secondary organic aerosols: The POLYSOA project. J Aerosol Med Pulm Drug Deliv. 2008;21(1):145–154. doi: 10.1089/jamp.2007.0655. [DOI] [PubMed] [Google Scholar]
- 6.Jang M, Ghio AJ, Cao G. Exposure of BEAS-2B cells to secondary organic aerosol coated on magnetic nanoparticles. Chem Res Toxicol. 2006;19(8):1044–1050. doi: 10.1021/tx0503597. [DOI] [PubMed] [Google Scholar]
- 7.Perraud V, et al. Nonequilibrium atmospheric secondary organic aerosol formation and growth. Proc Natl Acad Sci USA. 2012;109(8):2836–2841. doi: 10.1073/pnas.1119909109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Riipinen I, et al. Organic condensation: A vital link connecting aerosol formation to cloud condensation nuclei (CCN) concentrations. Atmos Chem Phys. 2011;11:3865–3878. [Google Scholar]
- 9.Shiraiwa M, Ammann M, Koop T, Pöschl U. Gas uptake and chemical aging of semisolid organic aerosol particles. Proc Natl Acad Sci USA. 2011;108(27):11003–11008. doi: 10.1073/pnas.1103045108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Shiraiwa M, Seinfeld JH. Equilibration timescale of atmospheric secondary organic aerosol partitioning. Geophys Res Lett. 2012;39:L24801. [Google Scholar]
- 11.Zelenyuk A, et al. Synergy between secondary organic aerosols and long-range transport of polycyclic aromatic hydrocarbons. Environ Sci Technol. 2012;46(22):12459–12466. doi: 10.1021/es302743z. [DOI] [PubMed] [Google Scholar]
- 12.Kamens R, Jang M, Chien C-J, Leach K. Aerosol formation from the reaction of α-pinene and ozone using a gas-phase kinetics-aerosol partitioning model. Environ Sci Technol. 1999;33:1430–1438. [Google Scholar]
- 13.Odum JR, Yu J, Kamens RM. Modeling the mass transfer of semivolatile organics in combustion aerosols. Environ Sci Technol. 1994;28(13):2278–2285. doi: 10.1021/es00062a011. [DOI] [PubMed] [Google Scholar]
- 14.Rounds SA, Pankow JF. Application of a radial diffusion model to describe gas/particle sorption kinetics. Environ Sci Technol. 1990;24:1378–1386. [Google Scholar]
- 15.Cappa CD, Wilson KR. Evolution of organic aerosol mass spectra upon heating: Implications for OA phase and partitioning behavior. Atmos Chem Phys. 2011;11:1895–1911. [Google Scholar]
- 16.Vaden TD, Imre D, Beránek J, Shrivastava M, Zelenyuk A. Evaporation kinetics and phase of laboratory and ambient secondary organic aerosol. Proc Natl Acad Sci USA. 2011;108(6):2190–2195. doi: 10.1073/pnas.1013391108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Vaden TD, Song C, Zaveri RA, Imre D, Zelenyuk A. Morphology of mixed primary and secondary organic particles and the adsorption of spectator organic gases during aerosol formation. Proc Natl Acad Sci USA. 2010;107(15):6658–6663. doi: 10.1073/pnas.0911206107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Virtanen A, et al. An amorphous solid state of biogenic secondary organic aerosol particles. Nature. 2010;467(7317):824–827. doi: 10.1038/nature09455. [DOI] [PubMed] [Google Scholar]
- 19.Virtanen A, et al. Bounce behavior of freshly nucleated biogenic secondary organic aerosol particles. Atmos Chem Phys. 2011;11:8759–8766. [Google Scholar]
- 20.Kuwata M, Martin ST. Phase of atmospheric secondary organic material affects its reactivity. Proc Natl Acad Sci USA. 2012;109(43):17354–17359. doi: 10.1073/pnas.1209071109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Saukko E, et al. Humidity-dependent phase state of SOA particles from biogenic and anthropogenic precursors. Atmos Chem Phys. 2012;12:7517–7529. [Google Scholar]
- 22.Abramson E, Imre D, Beránek J, Wilson JM, Zelenyuk A. Experimental determination of chemical diffusion within secondary organic aerosol particles. Phys Chem Chem Phys. 2013;15(8):2983–2991. doi: 10.1039/c2cp44013j. [DOI] [PubMed] [Google Scholar]
- 23.Martin ST. Phase transitions of aqueous atmospheric particles. Chem Rev. 2000;100(9):3403–3454. doi: 10.1021/cr990034t. [DOI] [PubMed] [Google Scholar]
- 24.Held IM, Soden BJ. Water vapor feedback and global warming. Annu Rev Energy Environ. 2000;25:441–475. [Google Scholar]
- 25.Hamed A, et al. The role of relative humidity in continental new particle formation. J Geophys Res-Atmos. 2011;116:D03202. [Google Scholar]
- 26.Koop T, Bookhold J, Shiraiwa M, Pöschl U. Glass transition and phase state of organic compounds: Dependency on molecular properties and implications for secondary organic aerosols in the atmosphere. Phys Chem Chem Phys. 2011;13(43):19238–19255. doi: 10.1039/c1cp22617g. [DOI] [PubMed] [Google Scholar]
- 27.Zobrist B, Marcolli C, Pedernera D, Koop T. Do atmospheric aerosols form glasses? Atmos Chem Phys. 2008;8:5221–5244. [Google Scholar]
- 28.Cavalli F, et al. Size-segregated aerosol chemical composition at a boreal site in southern Finland, during the QUEST project. Atmos Chem Phys. 2006;6:993–1002. [Google Scholar]
- 29.Han Z, Tang X, Zheng B. A PDMS viscometer for microliter Newtonian fluid. J Micromech Microeng. 2007;17:1828–1834. [Google Scholar]
- 30.Lin Y-Y, Lin C-W, Yang L-J, Wang A-B. Micro-viscometer based on electrowetting on dielectric. Electrochim Acta. 2007;52:2876–2883. [Google Scholar]
- 31.Srivastava N, Burns MA. Analysis of non-Newtonian liquids using a microfluidic capillary viscometer. Anal Chem. 2006;78(5):1690–1696. doi: 10.1021/ac0518046. [DOI] [PubMed] [Google Scholar]
- 32.Silber-Li ZH, Tan YP, Weng PF. A microtube viscometer with a thermostat. Exp Fluids. 2004;36:586–592. [Google Scholar]
- 33.Renbaum-Wolff L, Grayson JW, Bertram AK. Technical note: New methodology for measuring viscosities in small volumes characteristic of environmental chamber particle samples. Atmos Chem Phys. 2013;13:791–802. [Google Scholar]
- 34.Murray BJ, et al. Glass formation and unusual hygroscopic growth of iodic acid solution droplets with relevance for iodine oxide particles in the coastal marine boundary layer. Atmos Chem Phys. 2012;12:8575–8587. [Google Scholar]
- 35.Edgeworth R, Dalton BJ, Parnell T. The pitch drop experiment. Eur J Phys. 1984;5:198–200. [Google Scholar]
- 36.Cocker DR, III, Clegg SL, Flagan RC, Seinfeld JH. The effect of water on gas-particle partitioning of secondary organic aerosol. Part I: α-pinene/ozone system. Atmos Environ. 2001;35:6049–6072. [Google Scholar]
- 37.Saathoff H, et al. Coating of soot and (NH4)2SO4 particles by ozonolysis products of α-pinene. J Aerosol Sci. 2003;34:1297–1321. [Google Scholar]
- 38.Varutbangkul V, et al. Hygroscopicity of secondary organic aerosols formed by oxidation of cycloalkenes, monoterpenes, sesquiterpenes, and related compounds. Atmos Chem Phys. 2006;6:2367–2388. [Google Scholar]
- 39.Virkkula A, Van Dingenen R, Raes F, Hjorth J. Hygroscopic properties of aerosol formed by oxidation of limonene, α-pinene, and β-pinene. J Geophys Res-Atmos. 1999;104:3569–3579. [Google Scholar]
- 40.Kestin J, Solokov M, Wakeham WA. Viscosity of liquid water in the range -8 °C to 150 °C. J Phys Chem Ref Data. 1978;7:941–948. [Google Scholar]
- 41.Huff Hartz KE, et al. Cloud condensation nuclei activation of monoterpene and sesquiterpene secondary organic aerosol. J Geophys Res-Atmos. 2005;110:D14208. [Google Scholar]
- 42.Saathoff H, et al. Temperature dependence of yields of secondary organic aerosols from the ozonolysis of α-pinene and limonene. Atmos Chem Phys. 2009;9:1551–1577. [Google Scholar]
- 43.Ng NL, et al. Contribution of first- versus second-generation products to secondary organic aerosols formed in the oxidation of biogenic hydrocarbons. Environ Sci Technol. 2006;40(7):2283–2297. doi: 10.1021/es052269u. [DOI] [PubMed] [Google Scholar]
- 44.Chen X, Hopke PK. Secondary organic aerosol from α-pinene ozonolysis in dynamic chamber system. Indoor Air. 2009;19(4):335–345. doi: 10.1111/j.1600-0668.2009.00596.x. [DOI] [PubMed] [Google Scholar]
- 45.Bones DL, Reid JP, Lienhard DM, Krieger UK. Comparing the mechanism of water condensation and evaporation in glassy aerosol. Proc Natl Acad Sci USA. 2012;109(29):11613–11618. doi: 10.1073/pnas.1200691109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zahardis J, Petrucci GA. The oleic acid-ozone heterogeneous reaction system: Products, kinetics, secondary chemistry, and atmospheric implications of a model system - a review. Atmos Chem Phys. 2007;7:1237–1274. [Google Scholar]
- 47.Shiraiwa M, et al. The role of long-lived reactive oxygen intermediates in the reaction of ozone with aerosol particles. Nat Chem. 2011;3(4):291–295. doi: 10.1038/nchem.988. [DOI] [PubMed] [Google Scholar]
- 48.Smith GD, Woods E, DeForest CL, Baer T, Miller RE. Reactive uptake of ozone by oleic acid aerosol particles: Application of single-particle mass spectrometry to heterogeneous reaction kinetics. J Phys Chem A. 2002;106:8085–8095. [Google Scholar]
- 49.Pfrang C, Shiraiwa M, Pöschl U. Chemical ageing and transformation of diffusivity in semi-solid multi-component organic aerosol particles. Atmos Chem Phys. 2011;11:7343–7354. [Google Scholar]
- 50.Kirchstetter TW, Corrigan CE, Novakov T. Laboratory and field investigation of the adsorption of gaseous organic compounds onto quartz filters. Atmos Environ. 2001;35:1663–1671. [Google Scholar]
- 51.Shilling JE, et al. Particle mass yield in secondary organic aerosol formed by the dark ozonolysis of α-pinene. Atmos Chem Phys. 2008;8:2073–2088. [Google Scholar]
- 52.Tillmann R, et al. Influence of relative humidity and temperature on the production of pinonaldehyde and OH radicals from the ozonolysis of alpha-pinene. Atmos Chem Phys. 2010;10:7057–7072. [Google Scholar]
- 53.Kostenidou E, Lee BH, Engelhart GJ, Pierce JR, Pandis SN. Mass spectra deconvolution of low, medium, and high volatility biogenic secondary organic aerosol. Environ Sci Technol. 2009;43(13):4884–4889. doi: 10.1021/es803676g. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.