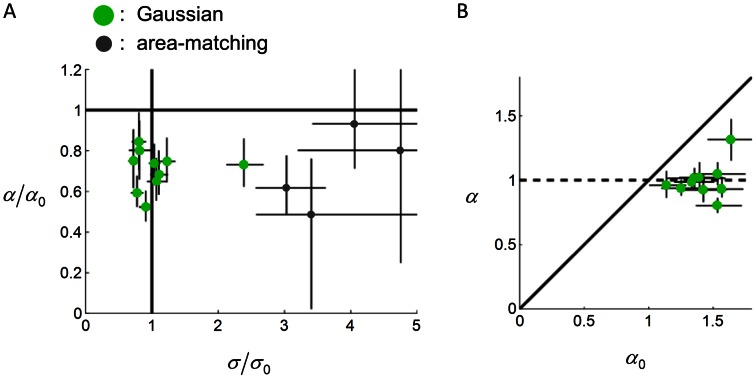
Figure 4. Subjects' models in probability choices in Experiment 1.

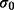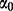Each circle denotes one subject. Error bars denote 95% confidence intervals. and are the variance and anisotropy parameters of the true distribution 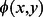(Eq. 3). and are their counterparts in the subject's model 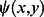(Eq. 4). A. 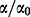plotted against 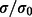. Among the 18 subjects, 10 subjects (the Gaussian type, in green) were better fit by the Gaussian model, who had internal variance close to true ( 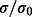close to 1) but who underestimated the vertical anisotropy of their true distribution (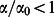). The remaining 8 subjects (the area-matching type, in gray) were better fit by the area-matching model, as if they were comparing the areas rather than the probabilities of hit of the targets. Four subjects of the area-matching type resulted in too large 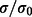(13, 19, 57, 889) and were not plotted. b. 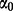plotted against for subjects of the Gaussian type. Note that was close to 1 regardless of the value of 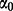for most subjects. That is, the distribution was incorrectly assumed to be isotropic in subjects' model.