Figure 6.

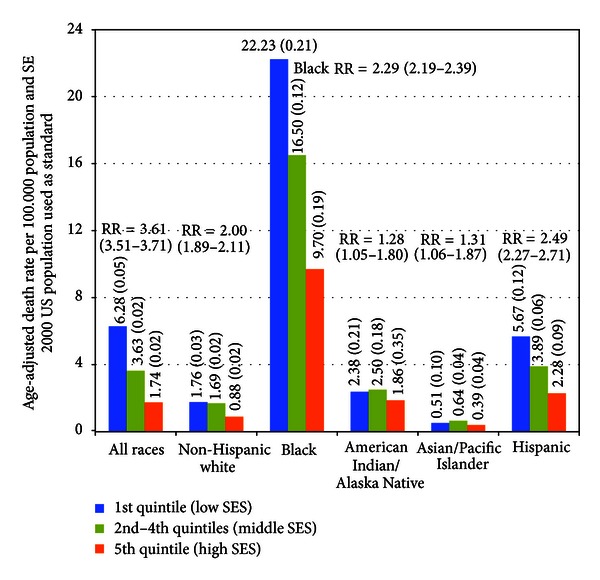
HIV/AIDS mortality by race/ethnicity and socioeconomic deprivation level, United States, 2005–2009. RR is ratio of mortality rate for the 1st quintile (low SES) to that for the 5th quintile (high SES). The standard normal Z test can be used to evaluate the statistical significance of the difference in mortality rates between any two groups at one point in time or to test for change in mortality rates between two time points for a specific group. If the absolute value of the Z-statistic = (R1 − R2)/SQRT[(SE  (R1))² + (SE  (R2))²] ≥ 1.96, then the difference is statistically significant at the 0.05 level. If the test statistic ≥2.58, then the difference in the rates is significant at the 0.01 level, where R1 is mortality rate for the first demographic group, R2 is mortality rate for the second demographic group, and SE (R1) and SE (R2) are the standard errors associated with R1 and R2, respectively. For example, during 2005–2009, the HIV/AIDS mortality rate for Hispanics in the most-deprived socioeconomic group (5.67) was 3.2 times higher than the corresponding rate for non-Hispanic whites (1.76), and this difference was statistically significant at the 0.01 level (computed Z-value = 31.61). The 95% confidence interval for a specific mortality rate can be constructed by using the formula = rate ± 1.96 * standard error.