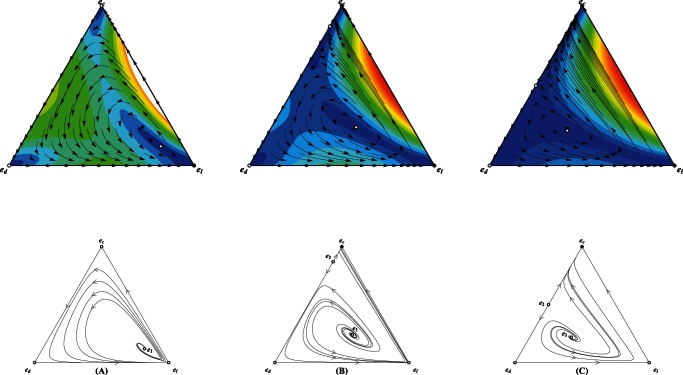
Figure 6. Triangle plots illustrating the population dynamics for defectors (), cooperators () and loners () for trajectories starting from all possible initial frequencies for the linear risk removal pattern.

Each vertex represents a homogeneous population of that pure strategy. 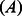For small interest rate , there is only one nontrivial fixed point (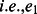) located inside the simplex 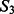. All trajectories starting from inside of the simplex 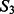invariable lead to the unique convergent equilibrium 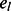. For modest , except 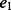, there also exists another nontrivial fixed point located in the line 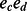(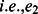). Instead the cooperators' attraction basin covers absolutely large fraction of the inside area of the simplex 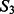, and loners' attraction basin is almost negligible. If defectors are abundant, the population dynamics oscillate around the unique unstable interior fixed point 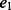with increasing amplitude and eventually converges to the full cooperative state 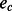. Otherwise, the population directly drives towards 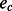. 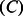Further increase in continue to expand the cooperators' attraction basin. It should be noted that even 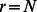, loners' attraction basin, albeit narrows, does not vanish. Relevant parameters 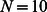, and 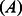, , .
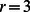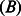
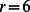
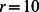