Figure 4.
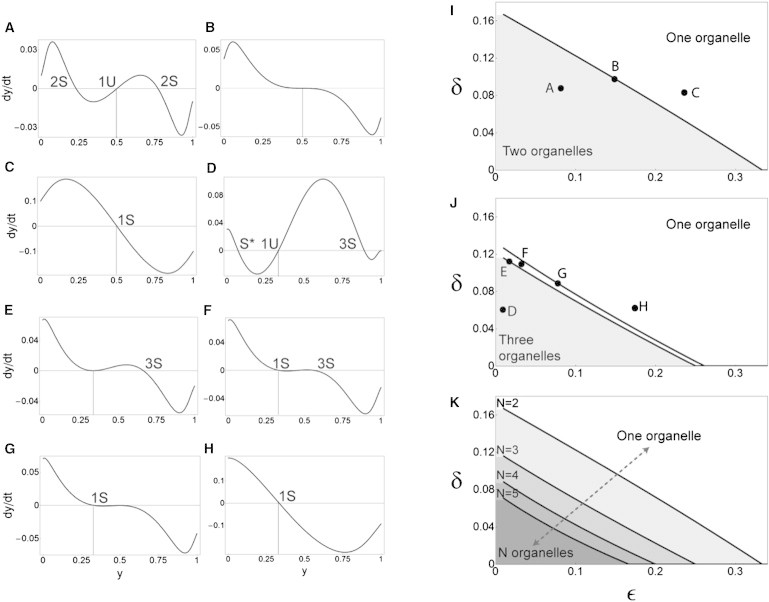
Larger organellar repertoires require greater molecular interaction specificity. We consider the N compartment, N coat, N SNARE case. The parameters δ and ε capture the strengths of cross-interactions: the lower their value, the higher the degree of molecular specificity. We restrict our attention to the 1D dynamical subsystem, in which compartments are equally sized and each compartment is labeled by a unique dominant SNARE whose amount is y(t). Time evolution is given by . (A–H) Graphs of dy/dt versus y corresponding to different points in δ-ε space. These graphs tell us about the existence of fixed points (where the graph crosses zero) and their stability (crossings with negative slope are stable and those with positive slope are unstable). The one-organelle fixed point is the uniform case in which y = 1/N (vertical dotted lines); it always exists but can be stable (1S) or unstable (1U). The N-organelle fixed point is the case in which dominant SNAREs emerge, so y > 1/N; it is always stable whenever it does exist (2S and 3S). Note that stability within the 1D subsystem is necessary but not sufficient for stability within the full system; for example, we never observe the subdominant fixed point y < 1/N (S*) in simulations. (A–C) N = 2. (D–H) N = 3. (I) For N = 2, we find a boundary that separates δ-ε space into two-organelle (shaded) and one-organelle (white) regions. The corresponding graphs of dy/dt are symmetric around y = 0.5, preventing more complex bifurcations. (J) For N ≥3 there are no symmetry constraints, so we find two bifurcation boundaries. In the shaded region bounded by the lower curve, we see only three-organelle behavior. Between the two curves, both one-organelle and three-organelle behaviors are stable, so the outcome depends on initial conditions, and across the upper curve we see only one-organelle behavior. (K) For N = 2, 3, 4, and 5, we show the curves that bound the shaded regions of always-N-organelle behavior. We see that as N increases, this region shrinks toward the origin.
