Figure 3.
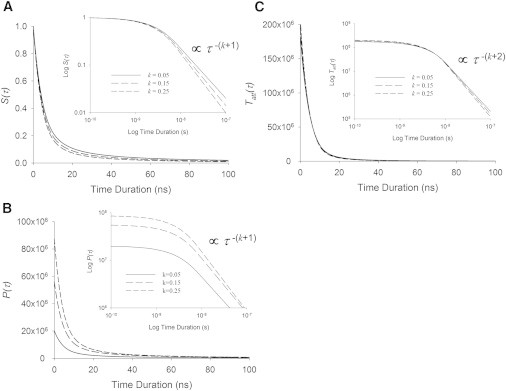
Probability density functions. (A) The probability that any already attached crosslink has been formed or has survived for a specific duration, τ, is described by S(τ), which we model with an inverse power law after a critical time tcrit. For illustration purposes, we use tcrit = 10 ns as might be expected from ionic bonds. This survival function always has unitary value at time zero. (B) The corresponding probability density function for the survival duration τ is given by P(τ), which is equivalent to S(τ) divided by the mean crosslink lifetime. (C) The probability density function for attached crosslink lifetimes, Tatt(τ), is proportional to the time-derivative of S(τ). (Insets) Log-log plots of these functions versus duration show linear relationships for crosslink durations longer than tcrit.
