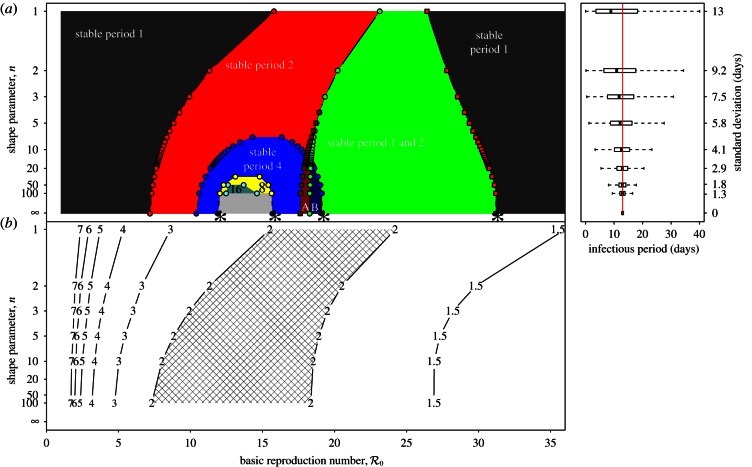
Figure 6.

Dynamical structure of the SIⁿR model with a mean infectious period 1/γ = 13 days. (a) Two-parameter (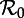 versus n) bifurcation diagram corresponding to the main branch of the one-parameter bifurcation diagrams shown in figure 4. Circles represent period-doubling (flip) bifurcations while squares denote tangent (fold) bifurcations as in figure 4. Regions are labelled according to the asymptotic dynamics on the main branch; the labels indicate which attractors are detected in each region of the 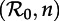plane: ‘stable period 1’ (a single annual attractor), ‘stable period 2’ (a single biennial attractor), ‘stable period 4’ (a single 4-year attractor), ‘8’ (a single 8-year attractor), ‘16’ (a single 16-year attractor), ‘stable period 1 and 2’ (coexistence of annual and biennial attractors), ‘A’ (coexistence of two distinct biennial attractors or coexistence of biennial and 4-year attractors) and ‘B’ (coexistence of annual and 4-year attractors). In the unlabelled light grey region below the region marked ‘16’, there are cascades of further period doublings that appear to end in chaos as n → ∞. The stars indicate bifurcation points that were estimated by extrapolation to n = ∞ rather than by direct calculations based on the fixed-delay model (see the electronic supplementary material, equation S12). (b) Contours of constant transient period (associated with the annual cycle) in the 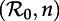plane (cf. black curves in figure 2b and in each panel of figure 5). In the hatched region, the transient period is phase-locked at precisely 2 years [37], whereas the transient period changes smoothly between the other contours. (Online version in colour.)