Figure 6.
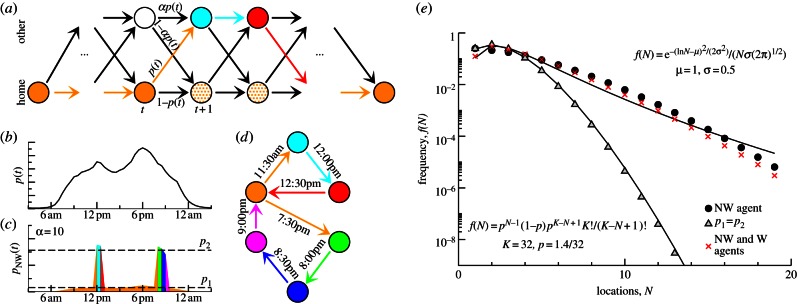
The introduced model is illustrated for a non-working agent. (a) The possible trajectories of an agent are shown. The agent starts the day at home and finishes it at home. At a given time t, depending on the actual location of the agent, the probability to be at home at time t + 1 is either 1 − p(t) or 1 − αp(t) with a parameter α and with probability p(t) and αp(t) the agent travels to another location. The filled circles and the coloured path is an exemplary trajectory. The time-dependent probabilities can be related to the circadian rhythm of activity, shown in (b). (c) The location-dependent probabilities for the exemplary agent with α = 10 are shown. The time-dependent probabilities can be approximated by only two values, p1 and p2 for being at home and being at another location. With this approximation, the model can be solved analytically. (d) The exemplary trajectory is converted into the corresponding motif with six locations and seven trips among them. (e) The daily number of visited locations obtained from the analytical model under three different conditions is shown. While the removal of workers does not change the tail of the log-normal distribution, α = 1 leads to a binomial distribution; thus periods of activities are key for the observed behaviour. Note that the absolute difference between analytical and numerical model is less than 0.01.
