Abstract
Purpose
Cross-relaxation imaging (CRI) is a family of quantitative magnetization transfer (MT) techniques that utilize images obtained with off-resonance saturation and longitudinal relaxation rate (R1) maps reconstructed by the variable flip angle (VFA) method. It was demonstrated recently that a significant bias in apparent VFA R1 estimates occurs in macromolecule-rich tissues due to MT-induced bi-exponential behavior of longitudinal relaxation of water protons. The purpose of this paper is to characterize theoretically and experimentally the resulting bias in the CRI maps and propose methods to correct it.
Theory
The modified CRI algorithm (mCRI) is proposed, which corrects for such bias and yields accurate parametric f, k, and R1 maps. Additionally, an analytical correction procedure is introduced to recalculate previously obtained parameter values.
Results
The systematic errors due to unaccounted bi-exponential relaxation can be characterized as overestimation of R1, bound pool fraction f, and cross-relaxation rate k, with a relative bias comparable with the magnitude of f. The phantom and human in vivo experiments demonstrate that both proposed mCRI and analytical correction approaches significantly improve accuracy of the CRI method.
Conclusion
Accuracy of the CRI method can be considerably improved by taking into account the contribution of MT-induced bi-exponential longitudinal relaxation into VFA R1 measurements.
Keywords: Magnetization transfer, two-pool model, cross-relaxation imaging, variable flip angle T1 mapping
INTRODUCTION
Magnetization transfer (MT) effect is commonly recognized as a source of important information about tissue microstructure due to its sensitivity to immobile macromolecular protons not detectable by conventional MRI (e.g., those associated with proteins and lipid bilayers of myelin, collagen matrix in cartilage, muscle fibers, etc) (1,2). Various approaches have been proposed to quantify the MT effect in-vivo including empirical indexes characterizing signal saturation due to MT (1,3,4) and methods for quantitative mapping of specific parameters describing MT within the two-pool model (2,5–15). The key parameters of interest in this model are associated with the state of macromolecular protons, which is characterized by their molar fraction (bound pool fraction, f), the forward rate constant describing cross-relaxation with water protons (k), and the transverse relaxation time T2B. Particularly promising findings were reported for the bound pool fraction, which was found to correlate with myelin content in neural tissues (16–19) and was shown to be capable of tracking age-related changes of WM myelination in animal studies (20).
One group of quantitative MT methods termed cross-relaxation imaging (CRI) (6,10,12) is specifically targeted at mapping the parameters f, k, and T2B or their subsets in isolation from relaxation properties of the water proton magnetization. Collectively, these techniques rely on the approximate two-pool pulsed MT formalism (6,10) where the action of off-resonance saturation pulses on the macromolecular proton pool is described by an effective time-independent saturation rate calculated for a square pulse with equivalent power and duration. Further, direct saturation of the free water proton pool is ether neglected (6) or estimated within the stationary approximation sufficiently far from resonance (10). These techniques allow 3D acquisition with clinically acceptable scan times and resolution based on a limited number of MT-weighted images obtained with variable off-resonance saturation. The common feature of CRI and other off-resonance qMT techniques is the need for complementary T1 mapping, which allows decoupling of the two-pool model parameters from the longitudinal relaxation rate R1=1/T1 (5–7,9,10,12). Due to the need for fast 3D acquisition, T1 maps are often generated using the variable flip angle (VFA) method with a spoiled gradient-echo (SPGR) sequence (21). It has been realized recently that the VFA method originally derived for the single-pool model inaccurately describes the SPGR signal, which often leads to biased R1 estimation in tissues with rich macromolecular content. This bias is due to unaccounted cross-relaxation caused by magnetization transfer between macromolecular and water protons, which leads to the bi-exponential behavior of longitudinal relaxation of water proton magnetization in such tissues (22). The cross-relaxation contribution was shown to dominate R1 of water in hydrated collagen (22) and more recently in neural tissues (23). Deviation of longitudinal relaxation from single-exponential behavior due to cross-relaxation significantly affects signal intensities in fast gradient-echo sequences (24,25) and introduces bias in VFA R1 measurements that depends on the pulse sequence parameters and may reach up to 14–15% in brain white matter (WM) (24).
Apart from biasing VFA R1 estimates, systematic errors from unaccounted bi-exponential relaxation may further propagate into the two-pool model parameters estimated by quantitative MT techniques such as CRI. On the other hand, unbiased determination of R1 values in tissues requires the knowledge about the rest of parameters of the two-pool model, which may not be practical for data correction within the VFA method alone (24). In this study, we propose the unified treatment of VFA and MT SPGR signals using a modified CRI analysis, which enables simultaneous correction of R1 and two-pool MT model parameters. In particular, we theoretically and experimentally characterize systematic errors in CRI caused by bi-exponential relaxation in VFA R1 mapping and demonstrate a new processing algorithm, which corrects for such errors and yields accurate parametric f, k, T2B, and R1 maps. Additionally, we propose an analytical correction procedure allowing recalculation of previously obtained cross-relaxation parameter values with acceptable residual errors.
THEORY
Analytical Theory of the SPGR Signal in the Presence of Cross-Relaxation
To estimate the effect of cross-relaxation on the apparent R1 measured by the VFA method, we employ the previously described pulsed steady-state formalism (6,10) in the simplified form, where no off-resonance saturation is applied. The matrix model of longitudinal magnetization (based on Eq. [1] in Ref. (10)) can be rewritten as:
| [1] |
, where corresponds to the longitudinal magnetization before the excitation pulse, are longitudinal magnetizations of free and bound protons, respectively, Meq = M0[1−f f]T is the vector of equilibrium magnetization, I is the identity matrix, the matrix E = exp(RTR) describes relaxation during repetition time TR and the diagonal matrix C = diag (Sf, Sb), Sf = cos α, Sb = 1 corresponds to instant rotation of the magnetization by an excitation pulse with the flip angle α. The relaxation matrix R is defined as follows:
| [2] |
where are longitudinal relaxation rates of the free and bound pool respectively. Applying the first-order approximation to exponential terms, Eq. [1] can be simplified to
| [3] |
Corresponding approximated expression for the observed signal can be explicitly written as follows:
| [4] |
We further assume that similar to earlier studies (6,12) that corresponds to the fast exchange conditions (26). With these assumptions, the signal intensity is expressed as:
| [5] |
Finally, the relaxation rate R1 can be neglected in the sum with a much larger term k/f, thus providing the signal equation
| [6] |
By comparing Eq. [6] with the first-order approximation of the Ernst equation (27) (not shown for brevity), the relationship between true R1 and its apparent value R1app estimated from VFA data becomes evident:
| [7] |
Equation [7] demonstrates that the bias in R1 caused by cross-relaxation is on the order of f and independent of the sequence parameters (TR and flip angles), if the first-order approximation is justified by a short TR. More general treatment for arbitrary sequence parameters can be found in Ref. (24,25).
Effect of Apparent R1 on the CRI Parameters
The next goal is to estimate systematic errors in the two-pool model parameters due to R1app in the CRI method. We start our analysis with a simplified CRI model (6), which allows analytical investigation of errors in fitted parameters in the regime where the direct saturation effect is negligible (Δ> 2.5 kHz) (28). According to this model, the ratio of signals with and without off-resonance saturation in a pulsed MT experiment can be expressed as
| [8] |
where
| [9] |
| [10] |
and WB is the saturation rate of the bound pool scaled by the duty cycle of the saturation pulse (s=tmt/TR, where tmt is the pulse duration). The saturation rate WB depends on the offset frequency and flip angle of the saturation pulse and is determined by the parameter T2B based on an appropriate spectral line shape model (typically SuperLorentzian (29)). If data are fitted in the form given by Eq. [8], the fitting algorithm searches for optimal parameters P, Q, and T2B regardless of an actual R1.
The effect of R1 errors on the two-pool model parameters originates from the dependence of the coefficients P and Q on R1 (Eqs. [9] and [10]). Accordingly, if R1app is supplied as input information, apparent values fapp and kapp will be obtained. The relationships between the true f and k and their apparent values can be derived from the conditions P(R1app, fapp)= P(R1, f) and Q(R1app, kapp)= Q(R1, k), which result in the simple recalculation formulas:
| [11] |
where the correction coefficient C is the same for f and k and depends on TR and flip angle:
| [12] |
The above analysis also suggests that R1 errors should not affect T2B, since WB is independent of R1 (6). We refer below to the recalculation formulas (Eqs. [11][12]) as CRI with 1st order correction.
Standard and Modified CRI Approaches
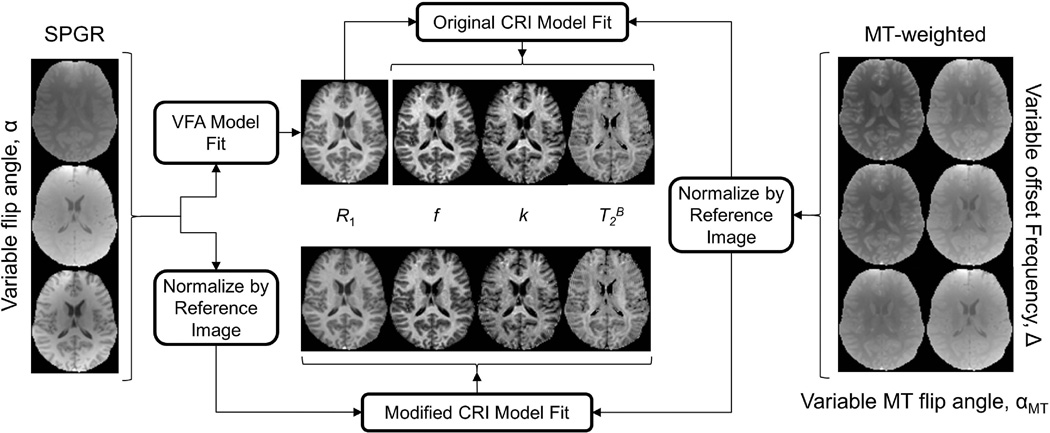
In the original CRI approach (10), reconstruction of parametric maps is performed in two stages (Fig. 1). During the first stage, R1 maps are calculated from VFA SPGR data by fitting the Ernst equation (21). During the second step, the matrix model of pulsed MT is fitted to MT-weighted data, while R1 is supplied as an external parameter. Prior to fit, MT data are normalized pixel-wise by an arbitrary reference image typically obtained without saturation. The purpose of such normalization is to reduce the number of free parameters in the fit by excluding a multiplicative factor commonly referred to as proton density, which absorbs the effects of spin concentration, T2* decay, and coil sensitivity. The normalized data are then fit to the corresponding ratio of analytical signal expressions with and without saturation . As an alternative to the standard CRI approach, we propose a modified CRI (mCRI) reconstruction algorithm to perform global fit of VFA and MT SPGR data simultaneously (Fig. 1). On the first stage, similarly to CRI, the normalization procedure is uniformly applied to VFA and MT data to exclude the common proton density term. Then, the normalized images are simultaneously fit to the corresponding ratios of analytical signal expressions with and without saturation using Eq. [1] from this paper and Eq. [1] from Ref. (10), respectively. Accordingly, the global fit simultaneously yields all remaining parameters (R1, f, k, T2B) and automatically takes into account the cross-relaxation contribution into VFA data (Fig. 1).
Figure 1.
Original CRI and modified CRI (mCRI) processing pipelines.
MATERIALS AND METHODS
Simulations
To estimate errors in the two-pool model parameters caused by the unaccounted bi-exponential relaxation, synthetic VFA and MT SPGR signal intensities were generated using Eq. [1] from this paper and Eq. [1] from Ref. (10), respectively. Then, datasets were fitted using the original CRI algorithm. The first-order correction formulas (Eqs. [7][11][12]) were also evaluated. Specific parameters used in simulations were taken from ROI measurements in the genu of corpus callosum (WM) and thalamus (GM) from full mCRI fit of the in vivo data presented below: 1) WM: R1 = 0.97s−1; f = 15.36 %; k = 2.70s−1; T2B = 9.84µs; 2) GM: R1 = 0.71s−1 ; f = 8.8% ; k = 1.57s−1 ; T2B = 10.21 µs. To study the effect of approximations of the 1st order correction in realistic imaging regime, pulse sequence parameters and sampling scheme in these simulations corresponded to those used in the in-vivo experiments detailed below.
Phantom Preparation
Five cross-linked BSA samples (98% bovine serum albumin, essentially fatty acid free, Sigma-Aldrich Corp., St. Louis, MO) were prepared with BSA percent weight of 10, 15, 20, 25, and 30 as described in (30). The BSA was dissolved in distilled water and was placed on ice for 10 minutes. Then, 50 µl/ml of an ice-cold 25% glutaraldehyde solution (Sigma-Aldrich Corp., St. Louis, MO) were added to the BSA solution while stirring with a syringe needle. The samples were kept at room temperature for two hours and then stored at 4° C.
Data Acquisition
Imaging experiments were carried out on a 3.0T GE Discovery MR750 (GE Healthcare; Waukesha, WI) using either an eight-channel transmit/receive knee coil (for phantom scans) or eight-channel phased array head coil (for a volunteer scan). All data were acquired with 3D MT-weighted SPGR sequence in a strong spoiling regime (31) (spoiling gradient area AG = 450 mT·ms/m, RF phase increment 169°). In phantom experiments, eight Z-spectroscopic datasets were acquired (TR/TE=37/2.3ms, excitation flip angle α=15°) with the 18 ms Fermi saturation pulse applied at the offset frequencies Δ = 2.5, 10, 18, 26 kHz with two nominal saturation flip angles αMT = 850° and 1300°. Additionally, four VFA SPGR datasets were acquired using the same sequence with Δ = 250 kHz to ensure that transmitter operates with identical gain settings (no MT effect is observed at this frequency) and flip angles optimized for the range of T1 values in the phantoms (α = 6°, 15°, 35°, and 50°). The SPGR dataset with the highest signal-to-noise ratio (α = 15°) was used as a reference image to normalize both Z-spectroscopic and VFA data as explained in the previous section. All datasets were acquired with FOV = 140×105×48mm and matrix = 128×96×24. Single-slice 2D inversion-prepared spin-echo (IR) data were collected to determine reference T1 values in the phantoms (TR/TE=5000/8.2ms, TI = 0.3, 0.5, 0.7, 0.9, 1.2, 1.6, 2s).
Informed written consent was obtained from a healthy volunteer in accordance with the local institutional policy. Eight Z-spectroscopic datasets were acquired using same pulse sequences (Δ = 2.5, 5, 9, 13 kHz, αMT = 500°, 1100°, α=10°). Four VFA datasets were acquired with flip angles α = 5°, 10°, 20°, and 30°. The image with α = 10° was used as a reference dataset. All Z-spectroscopic and VFA data were acquired with TR/TE=40/2.0ms, FOV =240×180×80mm and matrix = 128×96×42. The total scan time for this protocol was 35 minutes.
B0 and B1 maps were used to correct flip angle and local off-resonance frequency values in both phantom and volunteer studies. B1 maps were acquired using the actual flip angle imaging (AFI) method (32) (TR,1/TR,2/TE = 37/185/2.3 ms, α = 55°, FOV =240×180×80mm, matrix = 96×72×28) with the strong spoiling regime (31). B0 maps were calculated from the 3D fat-water separation method known as “iterative decomposition of water and fat with echo asymmetry and least squares estimation” (IDEAL) with FOV =240×180×80 mm and matrix = 256×256×42 (33). The scan time for these additional B0 and B1 mapping sequences was 10 minutes.
Image Processing and Analysis
The standard CRI processing workflow (Fig. 1) was implemented according to (10,34). In mCRI, all parametric maps were generated by fitting the normalized VFA and MT data simultaneously as described above (Fig. 1) using in-house-written C and MATLAB (MathWorks, Natick, MA) software utilizing a standard “lsqnonlin” function for nonlinear least squares voxel-based fitting (http://www.medphysics.wisc.edu/~samsonov/qmap). All quantitative parameter estimates in phantom scans and in-vivo were obtained from parametric maps in manually drawn regions-of- interest (ROI).
To study the association between BSA content and the bound pool fraction determined by different processing approaches, we performed linear regression analysis using the following model:
| [13] |
The strength of anticipated linear relationships was assessed using the Pearson’s correlation coefficient. We additionally tested if the intercept β0 is significantly different from zero (the anticipated value for f at BSA%=0). Statistical significance of differences between parameter measurements by CRI, mCRI, and CRI with first-order correction was assessed using paired two-tailed t-test.
RESULTS
Simulations
Table 1 shows the systematic errors in estimated parameters in WM and GM obtained from the original CRI method, mCRI, and CRI with first-order correction. As predicted by theory, the R1 bias propagates into f and k measurements but does not affect T2B, and it is most prominent for WM. A major portion of the biases are removed by proposed first-order correction, with R1 and f being corrected most efficiently (<1% residual error).
Table 1.
Simulated relative bias in two-pool MT model parameters obtained by the original CRI fit and its first-order correction due to unaccounted bi-exponential relaxation for WM and GM.
| Original CRI | 1st Order Correction | ||||||
|---|---|---|---|---|---|---|---|
| R1 | f | k | T2B | R1 | f | k | |
| WM | 16.92% | 12.42% | 15.20% | −0.08% | −0.96% | −0.42% | 2.04% |
| GM | 8.88% | 5.95% | 6.46% | −0.07% | −0.64% | −0.24% | 0.24% |
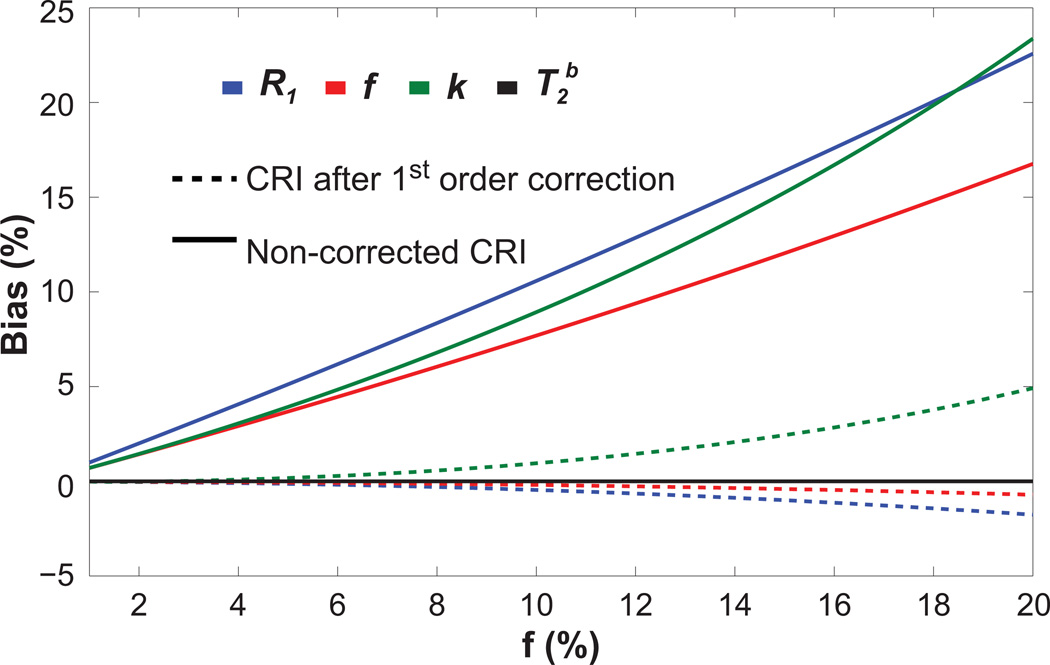
Figure 2 further illustrates the dependence of the biases on the fraction of bound protons in WM. Again, unaccounted bi-exponential relaxation in the SPGR signal model introduces a substantial bias to all quantitative MT parameters except for T2B when estimated by the original CRI method. These errors affect most significantly R1 values, then k and f values. They are steadily growing with the bound pool fraction as predicted by Eqs. [7][11]. First-order correction (Eqs. [11][12]) removes most of the bias for a wide range of f values, while the level of residual errors increases with an increase in f. First-order correction is less accurate for k values where the residual bias may reach up to ~5% for tissues with a higher macromolecular content.
Figure 2.
Relative bias in parameters estimated using original CRI before and after first-order correction vs. bound pool fraction. The other two-pool model parameters were fixed with values corresponding to WM.
Phantom Studies
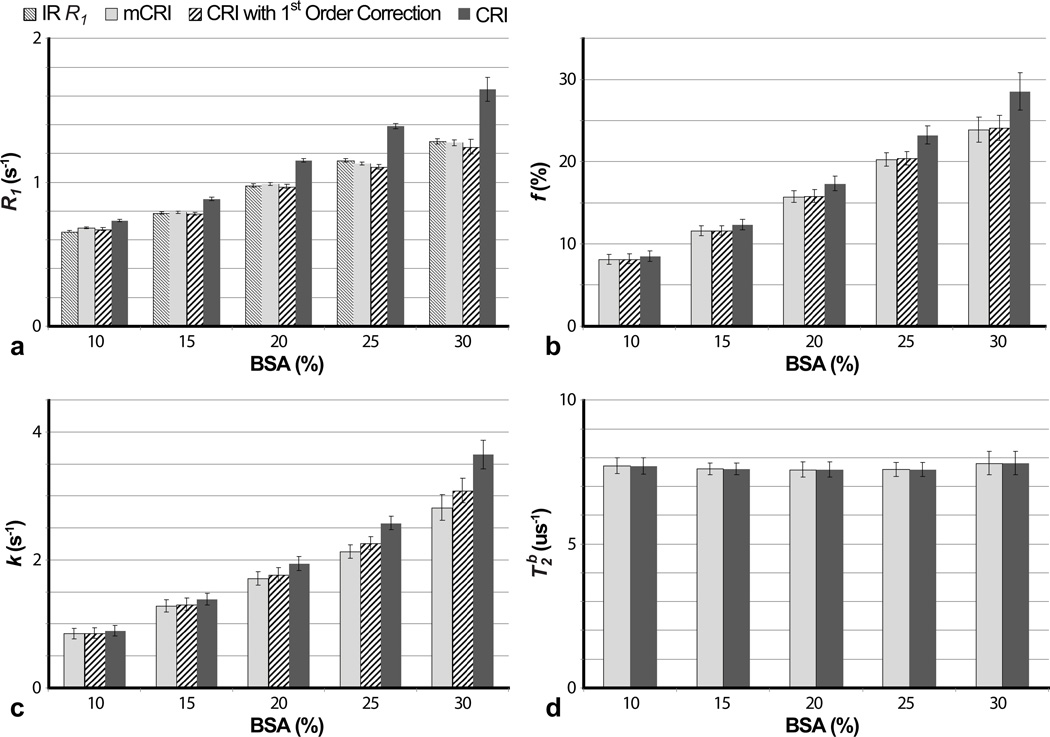
Figure 3 shows estimates of the two-pool MT model parameters in the BSA phantoms obtained using original CRI, mCRI, and CRI with first-order correction, as well as R1 values from a reference IR experiment. Both mCRI fit and the first-order correction of CRI fit provide good agreement with the reference IR R1 measurements, while the standard VFA method results in substantial discrepancy with IR R1 estimates. The difference between R1 values measured by the VFA method and IR method increases with BSA concentration as predicted by Eq. [7] and simulations (Fig. 2).
Figure 3.
Comparison of qMT parameters estimated using original CRI (without and with first-order correction) and mCRI in phantoms with different BSA concentrations. a: R1 measurements. IR R1 values are shown for reference. b,c,d: f, k, and T2B measurements, respectively. Error bars indicate standard deviations in ROI measurements taken from parameter maps.
Similarly, original CRI tends to overestimate bound pool fraction f and cross-relaxation rate k in the phantoms with a higher concentration of BSA. While first-order correction of f provides good agreement with the mCRI fit for all concentrations, an increased macromolecular content leads to a poorer first-order correction for k, as predicted by simulations (Fig. 2). T2B is consistent among different concentrations of BSA.
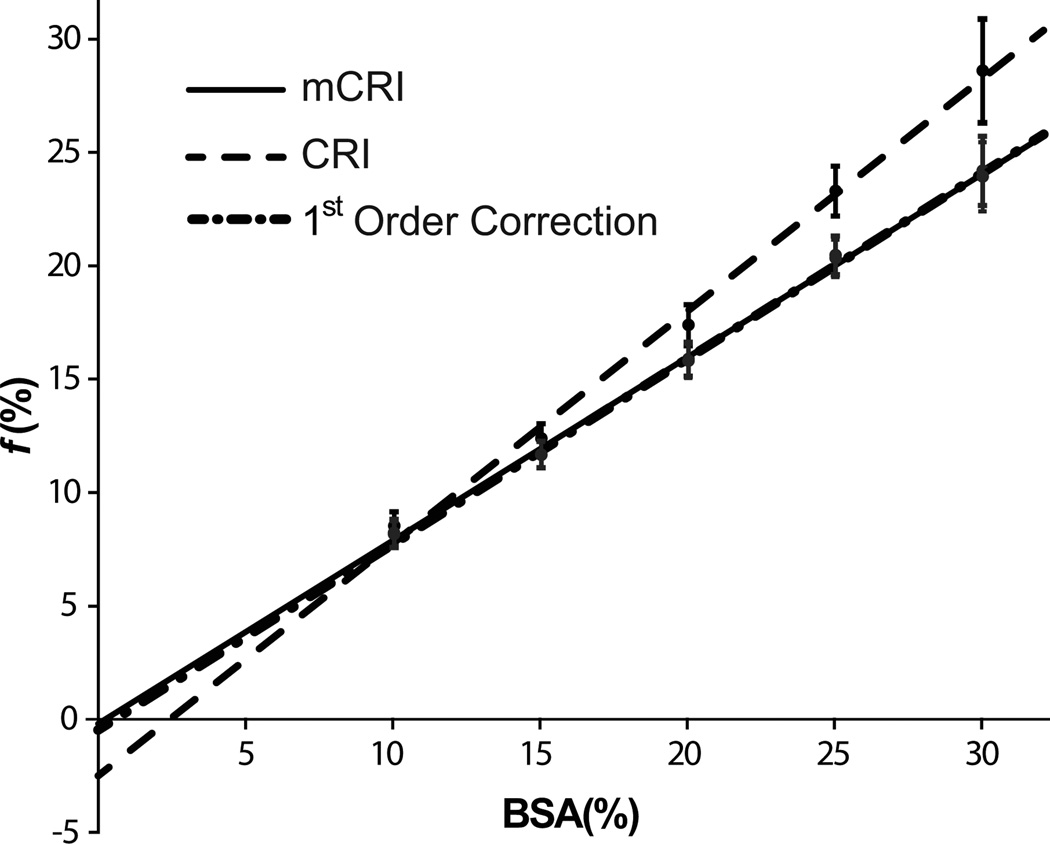
Figure 4 and Table 2 show results of linear regression analysis of f from phantom data. Bound pool fraction strongly correlates with BSA concentration for both CRI and mCRI, though the original CRI estimation lead to a somewhat weaker correlation (Table 2). The intercept of the fitted line for mCRI and the first-order correction is not significantly different from zero, thus reflecting the anticipated absence of the bound proton pool at 0% BSA concentration. At the same time, the intercept of the fitted line for original CRI is significantly different from zero and appears in the physically unrealistic range (~ −2.5%).
Figure 4.
Results of linear regression of bound pool fraction values derived by CRI, CRI with first-order correction, and mCRI vs. BSA concentration. Error bars indicate standard deviations in ROI measurements taken from parameter maps.
Table 2.
Results of linear regression analysis for bound pool fraction f in BSA phantoms.
| β0 (p-value) | β1 | R2 | |
|---|---|---|---|
| CRI | −2.46e-2±0.18e-3 (<10−4)* | 1.02e-2±8.63e-5 | 0.965 |
| 1st Order Correction | −0.25e-2±1.31e-3 (0.053) | 0.81e-2±6.16e-5 | 0.972 |
| mCRI | −0.14e-2±1.27e-3 (0.256) | 0.80e-2±6.00e-5 | 0.972 |
Asterisk (*) indicated that the difference between the intercept of the fitted line and zero is statistically significant.
In-Vivo Results
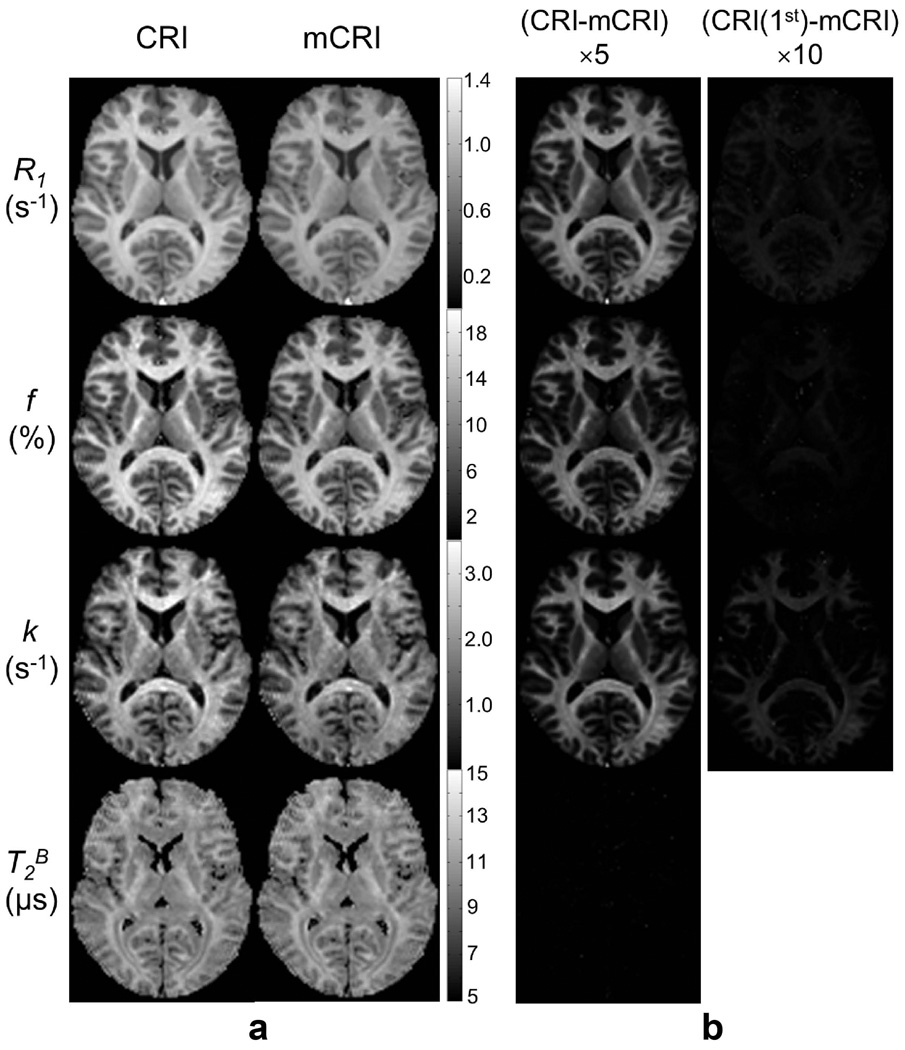
Figure 5 compares parametric maps obtained using the mCRI processing approach with original CRI and its first-order correction. Table 3 provides quantitative comparisons of qMT parameters in several WM and GM regions of interest. Processing with mCRI resulted in structurally similar, but quantitatively different parametric maps. For all parameters except for T2B, the error images reveal dependence of the bias on the macromolecular content as predicted by simulations and phantom studies. First-order correction efficiently minimizes the errors in f and R1. However, there is still visible residual error for k values after first-order correction, with most appreciable residue in WM regions, which is in agreement with simulations and phantom experiments (Figs. 2–3, Table 1). Statistical analysis of ROI data detected significant differences between CRI and mCRI for all parameters except for T2B in gray matter (Table 4). The effect of first-order correction was also significant for R1, f, and k. There were significant differences between mCRI and the first-order correction for R1 and k. These systematic errors as well as bias between mCRI and the first-order correction (Table 4) are consistent with the estimates predicted in simulations (Table 1).
Figure 5.
Parametric MT maps estimated using original CRI and mCRI (a), and errors of original CRI and its first-order correction (CRI (1st)) presented as difference maps with respect to mCRI (b). Note the consistency between levels of error in individual maps vs. macromolecular content as revealed by the bound pool fraction.
Table 3.
In vivo measurements of the two-pool MT model parameters using modified CRI (mCRI), original CRI, and CRI with first-order correction.
| Regions of Interest | mCRI | Original CRI | 1st Order Correction | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| R1 (s−1) | f (%) | k (s−1) | T2B (µs) | R1 (s−1) | f (%) | k (s−1) | T2B (µs) | R1 (s−1) | f (%) | k (s−1) | |
| White Matter | |||||||||||
| Cerebral peduncle | 0.933 | 14.81 | 2.064 | 11.560 | 1.088 | 16.54 | 2.353 | 11.556 | 0.928 | 14.73 | 2.097 |
| Corona radiata | 0.894 | 13.87 | 1.979 | 11.731 | 1.032 | 15.44 | 2.247 | 11.722 | 0.889 | 13.87 | 2.019 |
| Corpus callosum, genu | 0.966 | 15.36 | 2.702 | 9.844 | 1.133 | 17.28 | 3.115 | 9.836 | 0.959 | 15.30 | 2.758 |
| Corpus callosum, splenium | 0.942 | 14.92 | 2.517 | 10.197 | 1.105 | 16.75 | 2.890 | 10.187 | 0.940 | 14.90 | 2.570 |
| Frontal white matter | 0.898 | 13.93 | 2.161 | 11.231 | 1.036 | 15.49 | 2.445 | 11.223 | 0.892 | 13.90 | 2.196 |
| Internal capsule, anterior limb | 0.932 | 13.88 | 2.327 | 10.171 | 1.085 | 15.52 | 2.651 | 10.162 | 0.934 | 13.91 | 2.378 |
| Internal capsule, posterior limb | 0.903 | 15.33 | 2.048 | 11.836 | 1.057 | 17.20 | 2.356 | 11.829 | 0.896 | 15.26 | 2.092 |
| Middle cerebrallar peduncle | 0.855 | 14.28 | 1.993 | 10.473 | 0.999 | 15.99 | 2.220 | 10.443 | 0.855 | 14.33 | 1.990 |
| Occipital white matter | 0.924 | 14.79 | 1.898 | 10.628 | 1.080 | 16.73 | 2.198 | 10.621 | 0.919 | 14.89 | 1.956 |
| Gray Matter | |||||||||||
| Cerebral cortex | 0.739 | 6.6 | 1.102 | 9.023 | 0.781 | 6.89 | 1.122 | 8.987 | 0.729 | 6.58 | 1.072 |
| Caudate nucleus | 0.655 | 6.42 | 1.321 | 9.628 | 0.702 | 6.71 | 1.380 | 9.619 | 0.657 | 6.43 | 1.322 |
| Putamen | 0.710 | 7.29 | 1.432 | 9.736 | 0.770 | 7.66 | 1.512 | 9.728 | 0.714 | 7.29 | 1.439 |
| Substantia nigra | 0.788 | 8.59 | 1.371 | 9.817 | 0.863 | 9.14 | 1.462 | 9.808 | 0.789 | 8.59 | 1.375 |
| Thalamus | 0.707 | 8.77 | 1.569 | 10.208 | 0.780 | 9.36 | 1.682 | 10.198 | 0.711 | 8.8 | 1.583 |
Table 4.
Average relative bias between mCRI and CRI without and with first-order correction calculated from in vivo ROI measurements (Table 3).
| CRI | 1st Order Correction | ||||||
|---|---|---|---|---|---|---|---|
| R1 | f | k | T2B | R1 | f | k | |
| WM | 15.33% | 11.34% | 13.21% | 0.09% | −0.41% | −0.06% | 1.85% |
| GM | 7.94% | 5.39% | 5.2% | 0.15% | 0.03% | 0.05% | 0.06% |
Bold font indicates significantly different results (p<0.05).
DISCUSSION
MT imaging offers unique sensitivity to macromolecular content in tissues that cannot be assessed with conventional MRI. Accurate modeling of MT processes using the two-pool model is essential to yield specific parameters characterizing the macromolecular fraction in both normal and pathological conditions. This study demonstrates on the example of CRI, one of qMT methods based on SPGR pulse sequence, that separate treatment of VFA and MT data may cause non-negligible systematic errors in both R1 and quantitative MT parameters such as bound pool fraction f and cross-relaxation rate k. Specifically, this type of errors can be characterized as overestimation of R1, f, and k with a relative bias comparable with magnitude of f (Fig. 2, Tables 1,3,4). As the effect of the MT-induced bi-exponential longitudinal relaxation on the parameter estimates strongly depends on the macromolecular content in tissues (Fig. 2), the original CRI method and other qMT analysis techniques that do not take into account this effect may make interpretation of quantitative parameters inconsistent for different tissues types in different pathological conditions. It is also important to emphasize that apparent R1 values obtained from the standard single-compartment VFA technique are biased proportionally to f, and, hence, represent non-specific measures containing contributions from both intrinsic T1 relaxation properties of water protons in tissues and cross-relaxation.
We demonstrated that the accuracy of CRI estimates can be noticeably improved with the proposed combined data fit algorithm. Our modified CRI (mCRI) data processing approach does not require any additional measurements, thus maintaining the same time-efficiency as the original CRI technique. The mCRI method yields unbiased VFA R1 estimation, resulting in a decrease in R1 values by approximately 15% in WM and 8% in GM (Tables 3,4), which agrees well with the bias predicted earlier (24). In addition to the modified CRI fit, we have proposed simple analytical first-order approximated correction formulas allowing recalculation of original CRI-based parameters. The residual bias of such correction was shown both theoretically and experimentally to increase with macromolecular content due to violation of the first-order approximation. It may reach about 2% for k and 1% for f and R1 in the ranges of physiologically reasonable values for brain tissues. Nevertheless, first-order correction employed as a simple post-processing step in the original CRI processing pipeline (Fig. 1) may be a valid alternative to mCRI when either faster processing is required or previously computed parameter values need to be refined. Since the residual error after first-order correction increases with f, care must be taken when applying this approach to tissues with a markedly high macromolecular content. Additionally, a combination of either mCRI fit or the first-order correction with the recent single-point CRI technique (12) provides a promising approach for fast unbiased estimation of water proton R1 values within the VFA method (35). Finally, it should be pointed out that other sources of bias in the VFA method need to be eliminated in conjunction with the proposed methodology, similar to the procedures described in this study. Practically, VFA R1 mapping should be performed with a 3D sequence providing a uniform slab profile, B1 correction, and appropriate spoiling conditions (30,31).
The described analysis and correction methods have several potential limitations. One is the fundamental limitation of the two-pool model for accurate description of multiple exchanging compartments in biological tissues (36,37). Another is a specific assumption about the longitudinal relaxation rate of the bound pool R1B. Particularly, a recent study (26) demonstrated that widely adapted approximations (2,5) or (6,12) may considerably underestimate actual values of this parameter. Accordingly, this may cause an additional bias in the two-pool model parameters obtained using all qMT techniques based on the above assumptions about . However, it remains unclear at this point whether a faster longitudinal relaxation rate of the bound pool is an intrinsic property of macromolecular protons or a manifestation of more complex equilibriums involving water proton fractions with different mobility. The later hypothesis is logical in view of a shorter T1 found for the short-T2 water fraction commonly termed “myelin water” (36,38–41). Yet another limitation is the assumption about a negligible effect of the excitation pulse on the bound pool. This approximation is common for off-resonance pulsed quantitative MT methods employing low-angle excitation pulses (5–7,10,12), which cause negligible on-resonance saturation of the bound pool magnetization. However, as was shown earlier (25), the effect of on-resonance saturation should be taken into account for sequences with very short TR and high flip angles, the conditions typical for balanced steady state precession (bSSFP) imaging. In the two-pool formalism with pulsed excitation (Eq. [1]), on-resonance saturation of the bound pool can be taken into account by assigning an actual saturation factor Sb<1 in the diagonal matrix C. Corresponding Sb values can be estimated from the properties of the excitation pulse (duration and flip angle) and a spectral line shape of the bound pool (11,22). Based on this approach, we found for a particular pulse used in our sequence that on-resonance saturation of the bound pool results in an almost negligible effect on the accuracy of the two-pool model parameters determined by mCRI (<1% relative error for comparison between fits with actual Sb vs. Sb =1). However, this aspect of the technique could be important in the context of its standardization for future multi-center clinical studies since variations in the shape, duration, and flip angle of the excitation pulse may introduce a small but non-negligible bias dependent on a particular sequence implementation. Similarly, the approximation of the effect of the excitation pulse on the free pool by the term cosα in the matrix C (Eq. [1]) may not be absolutely correct due to relaxation during RF pulses of finite duration. Such an effect has been recently described (42), and its role for both VFA R1 and CRI parameter measurements remains to be investigated. In summary, while this study relies on the commonly accepted in the quantitative MT methodology approximations, future refinements of CRI accuracy seem to be possible based on accommodation of multi-compartment magnetization exchange schemes and a more rigorous analysis of magnetization dynamics during RF pulses.
CONCLUSIONS
This study demonstrates on the example of CRI that the accuracy of quantitative MT imaging can be considerably improved by taking into account the contribution of bi-exponential longitudinal relaxation into VFA R1 measurements. We have developed the two technical approaches allowing correction of biases in CRI parameter estimates caused by the MT-induced bi-exponential behavior of longitudinal relaxation of water spins based on either the global fit of both VFA and MT SPGR data to the two-pool signal model or the simple analytical recalculation formulas for key cross-relaxation parameters. While the choice between these techniques depends on a tradeoff between the correction accuracy and image processing speed, both approaches do not require extra data compared to the original CRI method.
ACKNOWLEDGMENTS
This work was supported by NIH NINDS R01NS065034 and NIBIB R21EB009908. We would like to thank Dr. Richard Kijowski for valuable comments.
REFERENCES
- 1.Wolff SD, Balaban RS. Magnetization transfer contrast (MTC) and tissue water proton relaxation in vivo. Magn Reson Med. 1989;10(1):135–144. doi: 10.1002/mrm.1910100113. [DOI] [PubMed] [Google Scholar]
- 2.Henkelman RM, Huang X, Xiang QS, Stanisz GJ, Swanson SD, Bronskill MJ. Quantitative interpretation of magnetization transfer. Magn Reson Med. 1993;29(6):759–766. doi: 10.1002/mrm.1910290607. [DOI] [PubMed] [Google Scholar]
- 3.Dousset V, Grossman RI, Ramer KN, Schnall MD, Young LH, Gonzalez-Scarano F, Lavi E, Cohen JA. Experimental allergic encephalomyelitis and multiple sclerosis: lesion characterization with magnetization transfer imaging. Radiology. 1992;182(2):483–491. doi: 10.1148/radiology.182.2.1732968. [DOI] [PubMed] [Google Scholar]
- 4.Helms G, Dathe H, Kallenberg K, Dechent P. High-resolution maps of magnetization transfer with inherent correction for RF inhomogeneity and T1 relaxation obtained from 3D FLASH MRI. Magn Reson Med. 2008;60(6):1396–1407. doi: 10.1002/mrm.21732. [DOI] [PubMed] [Google Scholar]
- 5.Sled JG, Pike GB. Quantitative imaging of magnetization transfer exchange and relaxation properties in vivo using MRI. Magn Reson Med. 2001;46(5):923–931. doi: 10.1002/mrm.1278. [DOI] [PubMed] [Google Scholar]
- 6.Yarnykh VL. Pulsed Z-spectroscopic imaging of cross-relaxation parameters in tissues for human MRI: theory and clinical applications. Magn Reson Med. 2002;47(5):929–939. doi: 10.1002/mrm.10120. [DOI] [PubMed] [Google Scholar]
- 7.Ramani A, Dalton C, Miller DH, Tofts PS, Barker GJ. Precise estimate of fundamental in-vivo MT parameters in human brain in clinically feasible times. Magn Reson Imaging. 2002;20(10):721–731. doi: 10.1016/s0730-725x(02)00598-2. [DOI] [PubMed] [Google Scholar]
- 8.Gochberg DF, Gore JC. Quantitative imaging of magnetization transfer using an inversion recovery sequence. Magn Reson Med. 2003;49(3):501–505. doi: 10.1002/mrm.10386. [DOI] [PubMed] [Google Scholar]
- 9.Tozer D, Ramani A, Barker GJ, Davies GR, Miller DH, Tofts PS. Quantitative magnetization transfer mapping of bound protons in multiple sclerosis. Magn Reson Med. 2003;50(1):83–91. doi: 10.1002/mrm.10514. [DOI] [PubMed] [Google Scholar]
- 10.Yarnykh VL, Yuan C. Cross-relaxation imaging reveals detailed anatomy of white matter fiber tracts in the human brain. Neuroimage. 2004;23(1):409–424. doi: 10.1016/j.neuroimage.2004.04.029. [DOI] [PubMed] [Google Scholar]
- 11.Ropele S, Seifert T, Enzinger C, Fazekas F. Method for quantitative imaging of the macromolecular 1H fraction in tissues. Magn Reson Med. 2003;49(5):864–871. doi: 10.1002/mrm.10427. [DOI] [PubMed] [Google Scholar]
- 12.Yarnykh VL. Fast macromolecular proton fraction mapping from a single off-resonance magnetization transfer measurement. Magn Reson Med. 2012;68(1):166–178. doi: 10.1002/mrm.23224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Dortch RD, Li K, Gochberg DF, Welch EB, Dula AN, Tamhane AA, Gore JC, Smith SA. Quantitative magnetization transfer imaging in human brain at 3 T via selective inversion recovery. Magn Reson Med. 2011;66(5):1346–1352. doi: 10.1002/mrm.22928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gloor M, Scheffler K, Bieri O. Quantitative magnetization transfer imaging using balanced SSFP. Magn Reson Med. 2008;60(3):691–700. doi: 10.1002/mrm.21705. [DOI] [PubMed] [Google Scholar]
- 15.Soellinger M, Langkammer C, Seifert-Held T, Fazekas F, Ropele S. Fast bound pool fraction mapping using stimulated echoes. Magn Reson Med. 2011;66(3):717–724. doi: 10.1002/mrm.22846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Underhill HR, Rostomily RC, Mikheev AM, Yuan C, Yarnykh VL. Fast bound pool fraction imaging of the in vivo rat brain: association with myelin content and validation in the C6 glioma model. Neuroimage. 2011;54(3):2052–2065. doi: 10.1016/j.neuroimage.2010.10.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Schmierer K, Tozer DJ, Scaravilli F, Altmann DR, Barker GJ, Tofts PS, Miller DH. Quantitative magnetization transfer imaging in postmortem multiple sclerosis brain. J Magn Reson Imaging. 2007;26(1):41–51. doi: 10.1002/jmri.20984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ou X, Sun SW, Liang HF, Song SK, Gochberg DF. Quantitative magnetization transfer measured pool-size ratio reflects optic nerve myelin content in ex vivo mice. Magn Reson Med. 2009;61(2):364–371. doi: 10.1002/mrm.21850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Dula AN, Gochberg DF, Valentine HL, Valentine WM, Does MD. Multiexponential T2, magnetization transfer, and quantitative histology in white matter tracts of rat spinal cord. Magn Reson Med. 2010;63(4):902–909. doi: 10.1002/mrm.22267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Samsonov A, Alexander AL, Mossahebi P, Wu YC, Duncan ID, Field AS. Quantitative MR imaging of two-pool magnetization transfer model parameters in myelin mutant shaking pup. Neuroimage. 2012;62(3):1390–1398. doi: 10.1016/j.neuroimage.2012.05.077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wang HZ, Riederer SJ, Lee JN. Optimizing the precision in T1 relaxation estimation using limited flip angles. Magn Reson Med. 1987;5(5):399–416. doi: 10.1002/mrm.1910050502. [DOI] [PubMed] [Google Scholar]
- 22.Edzes HT, Samulski ET. Cross relaxation and spin diffusion in the proton NMR or hydrated collagen. Nature. 1977;265(5594):521–523. doi: 10.1038/265521a0. [DOI] [PubMed] [Google Scholar]
- 23.Prantner AM, Bretthorst GL, Neil JJ, Garbow JR, Ackerman JJ. Magnetization transfer induced biexponential longitudinal relaxation. Magn Reson Med. 2008;60(3):555–563. doi: 10.1002/mrm.21671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ou X, Gochberg DF. MT effects and T1 quantification in single-slice spoiled gradient echo imaging. Magn Reson Med. 2008;59(4):835–845. doi: 10.1002/mrm.21550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bieri O, Scheffler K. On the origin of apparent low tissue signals in balanced SSFP. Magn Reson Med. 2006;56(5):1067–1074. doi: 10.1002/mrm.21056. [DOI] [PubMed] [Google Scholar]
- 26.Helms G, Hagberg GE. In vivo quantification of the bound pool T1 in human white matter using the binary spin-bath model of progressive magnetization transfer saturation. Phys Med Biol. 2009;54(23):N529–N540. doi: 10.1088/0031-9155/54/23/N01. [DOI] [PubMed] [Google Scholar]
- 27.Ernst RR, Anderson WA. Application of Fourier Transform Spectroscopy to Magnetic Resonance. Review of Scientific Instruments. 1966;37(1):93–102. [Google Scholar]
- 28.Portnoy S, Stanisz GJ. Modeling pulsed magnetization transfer. Magn Reson Med. 2007;58(1):144–155. doi: 10.1002/mrm.21244. [DOI] [PubMed] [Google Scholar]
- 29.Morrison C, Henkelman RM. A model for magnetization transfer in tissues. Magn Reson Med. 1995;33(4):475–482. doi: 10.1002/mrm.1910330404. [DOI] [PubMed] [Google Scholar]
- 30.Koenig SH, Brown RD, 3rd, Ugolini R. Magnetization transfer in cross-linked bovine serum albumin solutions at 200 MHz: a model for tissue. Magn Reson Med. 1993;29(3):311–316. doi: 10.1002/mrm.1910290306. [DOI] [PubMed] [Google Scholar]
- 31.Yarnykh VL. Optimal radiofrequency and gradient spoiling for improved accuracy of T1 and B1 measurements using fast steady-state techniques. Magn Reson Med. 2010;63(6):1610–1626. doi: 10.1002/mrm.22394. [DOI] [PubMed] [Google Scholar]
- 32.Yarnykh VL. Actual flip-angle imaging in the pulsed steady state: a method for rapid three-dimensional mapping of the transmitted radiofrequency field. Magn Reson Med. 2007;57(1):192–200. doi: 10.1002/mrm.21120. [DOI] [PubMed] [Google Scholar]
- 33.Reeder SB, Pineda AR, Wen Z, Shimakawa A, Yu H, Brittain JH, Gold GE, Beaulieu CH, Pelc NJ. Iterative decomposition of water and fat with echo asymmetry and least-squares estimation (IDEAL): application with fast spin-echo imaging. Magn Reson Med. 2005;54(3):636–644. doi: 10.1002/mrm.20624. [DOI] [PubMed] [Google Scholar]
- 34.Underhill HR, Yuan C, Yarnykh VL. Direct quantitative comparison between cross-relaxation imaging and diffusion tensor imaging of the human brain at 3.0 T. Neuroimage. 2009;47(4):1568–1578. doi: 10.1016/j.neuroimage.2009.05.075. [DOI] [PubMed] [Google Scholar]
- 35.Mossahebi P, Samsonov AA. Proc of ISMRM. Melbourne: 2012. Rapid and Accurate Variable Flip Angle T1 Mapping with Correction of On-Resonance MT Effects; p. 4267. [Google Scholar]
- 36.Stanisz GJ, Kecojevic A, Bronskill MJ, Henkelman RM. Characterizing white matter with magnetization transfer and T(2) Magn Reson Med. 1999;42(6):1128–1136. doi: 10.1002/(sici)1522-2594(199912)42:6<1128::aid-mrm18>3.0.co;2-9. [DOI] [PubMed] [Google Scholar]
- 37.Levesque IR, Pike GB. Characterizing healthy and diseased white matter using quantitative magnetization transfer and multicomponent T(2) relaxometry: A unified view via a four-pool model. Magn Reson Med. 2009;62(6):1487–1496. doi: 10.1002/mrm.22131. [DOI] [PubMed] [Google Scholar]
- 38.Does MD, Gore JC. Compartmental study of T(1) and T(2) in rat brain and trigeminal nerve in vivo. Magn Reson Med. 2002;47(2):274–283. doi: 10.1002/mrm.10060. [DOI] [PubMed] [Google Scholar]
- 39.Koenig SH, Brown RD, 3rd, Spiller M, Lundbom N. Relaxometry of brain: why white matter appears bright in MRI. Magn Reson Med. 1990;14(3):482–495. doi: 10.1002/mrm.1910140306. [DOI] [PubMed] [Google Scholar]
- 40.MacKay A, Whittall K, Adler J, Li D, Paty D, Graeb D. In vivo visualization of myelin water in brain by magnetic resonance. Magn Reson Med. 1994;31(6):673–677. doi: 10.1002/mrm.1910310614. [DOI] [PubMed] [Google Scholar]
- 41.Deoni SC, Rutt BK, Arun T, Pierpaoli C, Jones DK. Gleaning multicomponent T1 and T2 information from steady-state imaging data. Magn Reson Med. 2008;60(6):1372–1387. doi: 10.1002/mrm.21704. [DOI] [PubMed] [Google Scholar]
- 42.Boulant N. T1 and T2 effects during radio-frequency pulses in spoiled gradient echo sequences. J Magn Reson. 2009;197(2):213–218. doi: 10.1016/j.jmr.2008.12.023. [DOI] [PubMed] [Google Scholar]