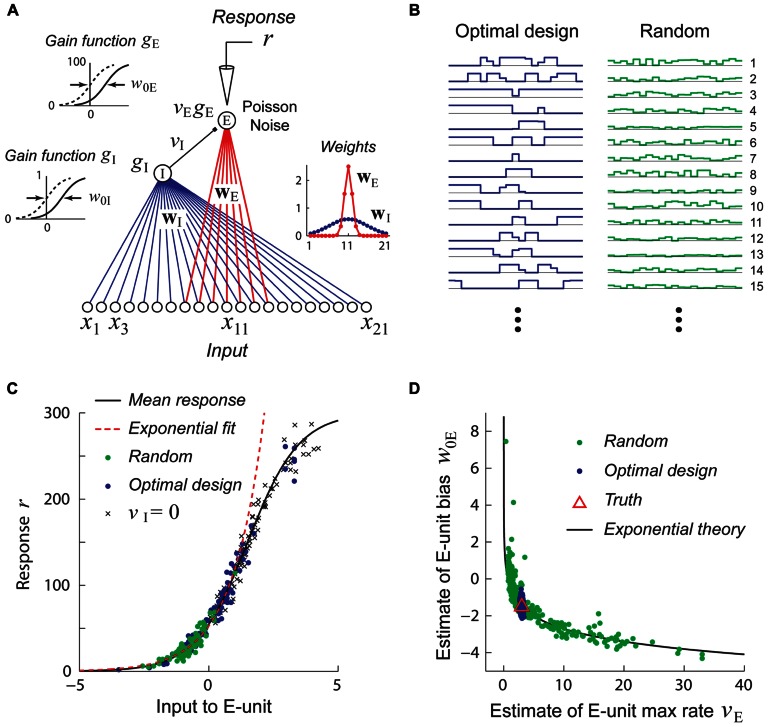
FIGURE 5.

Stimuli which are adaptively optimized for accurate parameter estimation can be more effective than random stimuli for recovering non-linear models. Adapted with permission from DiMattina and Zhang (2011). (A) A simple center-surround neural network consisting of a narrowly integrating excitatory output unit (E-unit) which receives inhibitory input from a broadly integrating interneuron (I-unit). (B) Examples of optimally designed (left) and random (right) stimuli. Note that the optimally designed stimuli exhibit complex correlated structure. (C) Random stimuli (green dots) only drive the E-unit over a limited range of its gain function (black curve) which may be well approximated by an exponential function (red dashed line). This is due to inhibition from the I-unit, as can be seen by setting v_I = 0 (crosses). By contrast, optimally designed stimuli (blue dots) drive the gain function over its full range. (D) Estimates attained from training with random stimuli (green dots) exhibit continuous parameter confounding between the output weight and bias, as predicted by the exponential theory (black curve). In contrast, estimates attained from optimally designed stimuli accurately recover the true parameters (red triangle).