On the Accuracy of Unwarping Techniques for the Correction of Susceptibility-Induced Geometric Distortion in Magnetic Resonance Echo-Planar Images

Abstract

Rapid and efficient imaging of the brain to monitor brain activity and neural connectivity is performed through functional MRI and diffusion tensor imaging (DTI) using the Echo-planar imaging (EPI) sequence. An entire volume of the brain is imaged by EPI in a few seconds through the measurement of all k-space lines within one repetition time. However, this makes the sequence extremely sensitive to imperfections of magnetic field. In particular, the error caused by susceptibility induced magnetic field inhomogeneity accumulates over the duration of phase encoding, which in turn results in severe geometric distortion (warping) in EPI scans. EPI distortion correction through unwarping can be performed by field map based or image based techniques. However, due to the lack of ground truth it has been difficult to compare and validate different approaches. In this paper we propose a hybrid field map guided constrained deformable registration approach and compare it to field map based and image based unwarping approaches through a novel in-vivo validation framework which is based on the acquisition and alignment of EPI scans with different phase encoding directions. The quantitative evaluation results show that our hybrid approach of field map guided deformable registration to an undistorted T2-weighted image outperforms the other approaches.

I. Introduction

Echo-planar imaging (EPI) is among the most widely used magnetic resonance imaging (MRI) sequences which constitutes the basis for some of the most important imaging protocols, such as functional MRI and diffusion weighted MRI. Consequently EPI plays a critical role in studying brain functional and structural connectivity [1] and white matter tractography. The applications of brain connectivity analysis in neuroscience, neuropathology, and neurosurgical planning are rapidly emerging thus the accuracy of EPI image analysis is crucial.

The entire brain volume is imaged by EPI in a few seconds. This provides the time resolution required for monitoring brain activity in fMRI and also for efficient measurement of water diffusion in diffusion weighted imaging for white matter tractography. The rapid acquisition in EPI is achieved by collecting all the k-space lines of a 2D plane within one repetition time. The cost for this rapid acquisition is extreme sensitivity to errors caused by field inhomogeneity [2]. Magnetic field inhomogeneity is caused by different susceptibility of air and tissue in areas near sinuses. As Jezzard and Balaban showed [3] the effect of field inhomogeneity is negligible in regular gradient echo and spin echo sampling strategies where one k-space line is acquired per phase encoding step, however, the effect is significant in EPI. The accumulation of error over the phase encoding, results in severe geometric distortions in EPI as voxel shifts by signal stretching or shrinking in the phase encoding direction. These artifacts may cause voxel shifts of up to 10 mm in areas such as prefrontal, orbitofrontal, temporal, and inferior cerebellar regions of the brain [2].

A common approach for geometric distortion correction in EPI is based on physical analysis and the acquisition of dual echo gradient echo images which provide an estimate of magnetic field map through data acquisition at two different echo times [4]. The geometric distortion correction using field map is performed through voxel shift unwarping directly computed from the estimated phase field map value at each voxel. The accuracy of this approach is highly dependent on the availability of accurate field map scans as well as the required image processing steps.

An alternative approach to field map based distortion correction is image-based deformable registration [5]. For an earlier review of the literature on field map-based and image-based approaches along with various validation strategies see [6]. Hybrid field map guided deformable registration techniques were proposed in [7] and [8]. Gholipour et al. developed average field map image template [9] and proposed field map guided deformable registration in the absence of field map images for individual subjects [6].

There have been more recent studies on deformable registration for distortion correction [10], and enhanced field mapping [11]; however the relative effectiveness of different approaches has not been properly addressed due to the lack of ground truth. Very recently Embleton et al. [12] and Holland et al. [13] developed correction techniques based on acquisitions with reversed phase encoding directions. While the acquisition of large series of EPI images with opposite phase encoding directions complicates fMRI and DTI protocols, the alteration of phase encoding direction provides a novel strong basis for the validation of different approaches, as proposed in this article.

In this study we use EPI acquisitions with different phase encoding directions for validation only. Within this framework we report comparative evaluation of field map-based and image-based correction techniques as compared to field map guided deformable registration. Our proposed hybrid method involves deformable registration of EPI to a high-resolution undistorted T2-weighted structural image, thus does not require any modification or extension of EPI scans or the acquisition of EPI with alternative phase encodings. The methods are discussed in section II. The invivo validation results reported in section III indicate that our field map guided deformable registration approach results in better alignment of EPI scans and also generates higher similarity of EPI to T1-weighted anatomic scans, which indicates better distortion correction.

II. Methods

A. Field map based unwarping

The analysis in [3] shows that the effect of field inhomogeneity is negligible in the frequency encoding direction of EPI but results in severe geometric warping in the phase encoding direction. EPI images can be unwarped using the information about magnetic field inhomogeneity in the form of phase field maps. According to the analysis in [3] voxel shift (in millimeters) along the phase encoding direction at a location r is proportional to the measured field inhomogeneity (in Hz) divided by the effective bandwidth per voxel, that is Δy_r = (2π. ΔT_E. B_pe)⁻¹ φ_r. Δq_y, where φ_r is the unwrapped phase field map value (in radians) at the voxel location r, ΔT_E is the difference in echo times of the dual echo gradient echo field map acquisition (in seconds), B_pe is the bandwidth in Hz/pixel, and Δq_y is the voxel spacing of the EPI image along the phase encoding direction in millimeters/pixel. The intensity values at voxels are then corrected by the Jacobian of the unwarping model to account for the effect of signal stretching or shrinking. We refer to this method as field map unwarping (FMU).

B. Image based unwarping

Image based unwarping is performed through deformable registration of EPI to an undistorted structural scan. Considering the EPI image as the source I_s and the structural image as target I_t we formulate the registration problem as the maximization of a similarity cost function between the transformed Jacobian-corrected EPI image and the target image to define the unwarping transformation T. The registration problem is thus written as

$$T_{\mathit{opt}}={\mathrm{argmax}}_{T\in \mathit{T}}\mathit{Sim}(I_t,J_{T}T(I_s\left)\right)$$ (1)

where J_T is the Jacobian of the transformation image.

We use a unidirectional transformation model based on a regular grid of control points with cubic B-Spline kernel interpolation:

$$T(y;p)=\sum _j{p}_j{\beta }^{\left(3\right)}\left(\frac{x-c_{\mathit{jx}}}{\Delta q_x}\right){\beta }^{\left(3\right)}\left(\frac{y-c_{\mathit{jy}}}{\Delta q_y}\right){\beta }^{\left(3\right)}\left(\frac{z-c_{\mathit{jz}}}{\Delta q_z}\right)$$ (2)

where β⁽³⁾(.) is the cubic B-spline kernel function, p is a vector of the displacement parameters p_j of the control points centered at locations (c_jx, c_jy, c_jz), (x, y, z) are the locations of the image points, and (Δq_x, Δq_y, Δq_z) is the voxel spacing of the source image.

Based on the physics of the problem the deformation field is regularized to warp the image significantly in the phase encoding direction as needed but not in the other directions. Without loss of generality we assumed y to be the phase encoding axis. With strong regularization, the deformation field will be a unidirectional transformation similar to [5]. Due to the differences in the contrast of EPI and structural MRI scans we use mutual information (MI) as the similarity measure. MI quantifies the nonlinear relationship between the intensity values of the images thus performs better than sum of square differences and normalized cross correlation in this application. We refer to this method as DR.

An alternative image-based method for EPI images specifically acquired with opposite phase encoding direction is to optimize a cost function between two EPI images to compute one unwarping model applied to the images in opposite directions. This approach has been recently proposed in [13]. We also implemented a similar method based on symmetric deformable registration of two EPI images of opposite phase encoding directions.

Finally we combine field map and image based approaches for field map guided deformable registration. The transformation model T is initialized with field map unwarping as discussed in section II.A. Deformable registration is then applied with constraints computed from the phase field map image. The constraints on control point parameters were defined through weighted kernel averaging of neighborhood voxels of the phase field map values. We refer to this method as FMG-DR.

III. Results

A. Data Acquisition

Data for the experiments in this study was acquired on a Siemens Trio 3 Tesla scanner with a 32 channel head coil. The data acquisition protocol involved a T1-weighted sagittal MPRAGE scan with a high resolution of 0.5×0.5×1 mm³, an axial T2-weighted fast spin echo scan with a resolution of 0.4×0.4×2.5 mm³, and 45-direction diffusion weighted MRI with five images with b=0s/mm²., and a spatial resolution of 1.7×1.7×2 mm³. The diffusion weighted images were acquired with a single-shot spin-echo EPI sequence, and were repeated with different phase encoding directions, i.e. anterior-to-posterior (A-to-P), posterior-to-anterior (P-to-A), and right-to-left (R-to-L), for validation. A dual echo gradient echo field map image was acquired in each experiment with echo times of 5.19 ms, 7.65 ms, and a resolution of 3.5×3.5×3 mm³. An unwrapped phase field map image was generated by the scanner for this sequence. Fig. 1 shows examples of the acquired data; the geometric distortion in EPI scans is severe in the inferior frontal, temporal, and cerebellar regions.

Fig. 1.

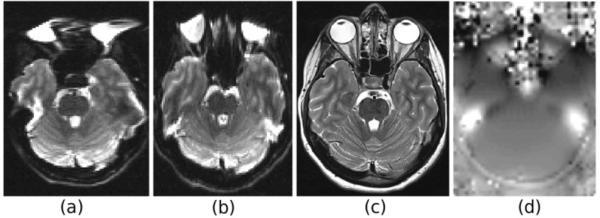
Susceptibility-induced magnetic field inhomogeneity causes geometric distortions along the phase encoding direction of EPI scans: (a) and (b) axial slice of B0 images of a DTI sequence with right-to-left and posterior-to-anterior phase encoding directions, respectively. (c) is an undistorted high-resolution T2-weighted fast spin echo MRI used as anatomic reference, and (d) is the corresponding phase field map image.

B. Quantitative in-vivo evaluation and comparison

For quantitative evaluation each pairs of EPI images in each experiment were averaged voxel-by-voxel. If the distortion in the images is perfectly corrected the geometry of the original and average images should match and the intensity differences between the images should be acquisition noise. We applied FMU, DR, and FMG-DR to all the EPI images in each experiment and computed the difference between the original images and the average. Fig. 2 shows color-coded intensity differences between these images before correction (a), after FMU (b), and after FMG-DR (c). The difference values below 40 were considered too small and set transparent for better visualization.

Fig. 2.

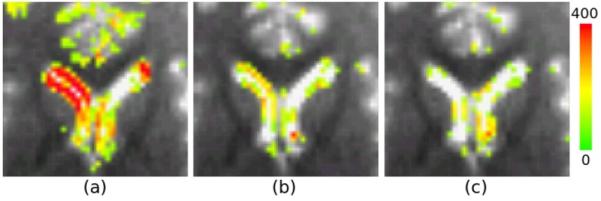
Color-coded intensity value differences between an original EPI image and the average of a pair of EPI images acquired with A-to-P and R-to-L phase encoding directions. Overlay values of less than 40 were set transparent.

For quantitative evaluation we compute the peak signal to noise ratio (PSNR) and mean absolute error (MAE) between pairs of EPI scans before and after unwarping with different methods. The results have been reported in Table 1. Mutual information (MI) computed between the EPI scans and the reference undistorted T1-weighted structural scans have also been presented in this Table. Note that the best values in each column have been highlighted in bold. All measures show that the discrepancy between the differently distorted EPI images was lower after FMG-DR, which in-turn indicates that the geometric distortions were better compensated with this method. Note that the error measures are averaged over the entire brain image. The compensation of distortion has been in fact much more prominent in the distorted region, as observed in Fig. 2.

Table 1.

Quantitative intensity difference and mutual information similarity measures computed between EPI scans and the average EPI scans and the reference T1-weighted scans.

	EPI-to-EPI		MI
Method	PSNR (dB)	MAE	to EPI	to T1W
No correction	27.5	24.3	0.554	0.375
FMU	28.0	22.0	0.589	0.384
DR	27.9	22.4	0.578	0.384
FMG-DR	28.4	20.9	0.590	0.387

Next we computed the sharpness of the average of EPI scans and the similarity of the average to the T1-weighted scans. As discussed before, if there is discrepancy between the EPI images, the average image becomes blurred, while if the EPI images perfectly match the average image will be sharp. We use two sharpness measures which are robust to noise [14]. The values are shown in Table 2. Again, all the measures indicate that geometric distortions have been more effectively compensated with the FMG-DR method.

Table 2.

Quantitative sharpness measures and mutual information between the average of EPI scans and T1-weighted reference scans.

Method	M1	M2	MI to T1W
No correction	3.33×109	39970	0.407
FMU	3.79×109	44582	0.416
DR	3.41×109	41890	0.414
FMG-DR	3.83×109	45119	0.433

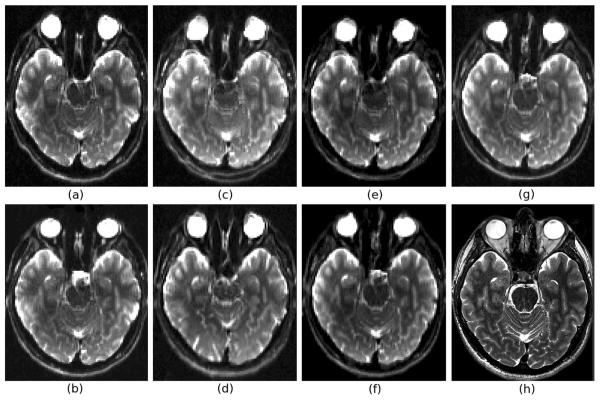
Fig. 3 shows typical results of unwarping with different techniques. The visualized axial slice of the images contains parts of the inferior frontal, temporal lobes, and inferior posterior distortion regions all together. The amount of distortion in these regions is observed by the mismatch between the EPI images overlaid through averaging in images (c) to (g). This mismatch is clearly observed in the boundaries of the brain in the posterior bone of the skull, and the orbits. (a) and (b) show one of the EPI images before any correction and after FMG-DR unwarping, respectively. (c) shows the average of two EPI scans with A-to-P and P-to-A phase encoding directions before correction, (d) shows the average image after symmetric constrained deformable registration of the pairs of the oppositely distorted EPI scans without an undistorted reference image, (e), (f) and (g) show average EPI images after FMU, DR, and FMG-DR, respectively. (h) shows a reference undistorted FSE scan.

Fig. 3.

EPI unwarping on a pair of B0 DTI images acquired with opposite phase encoding direction. This axial slice is chosen for visualization as it shows the intersection of several distorted regions, i.e. inferior frontal region, temporal lobes. The geometric distortions and the mismatch between the pairs of EPI images are obvious around the cortex, in orbits, and also in the bones at the back of the skull; (a) is an original image, (b) is the image after FMG-DR unwarping, (c) to (g) show the average of the two pairs of images; (c) is before any correction, (d) is after symmetric deformable registration of the two EPI scans, (e) is after DR, (f) is after FMU, and (g) is after FMG-DR. (h) shows the corresponding slice of the undistorted high-resolution T2-weighted FSE scan. The mismatch between the pairs of EPI images due to geometric distortion in opposite directions is observed in (c) to (e). On the other hand, the images are well matched in (g) which indicates that the geometric distortion is properly corrected using the FMG-DR method.

IV. Conclusion

Using a strong novel validation framework based on the alignment of EPI acquisitions with different phase encoding directions, we evaluated and compared three approaches to EPI unwarping for geometric distortion correction. The quantitative in-vivo validation criteria were independent of the methods used for distortion correction. The obtained results indicate that a hybrid method consisting of field map guided deformable registration of EPI to undistorted T2-weighted structural MRI generates the best match between pairs of differently distorted EPI images, and also between EPI images and a high-resolution T1-weighted anatomical scan. Geometric distortion correction in EPI is critical for precise mapping of EPI data to brain anatomy in the localization of brain activity, functional maps, and also for accurate analysis of neural connectivity and mapping white matter tracts to brain regions. This is particularly important in labeling and analyzing white matter tracts based on automatic brain segmentation. The methods developed in this article are available as part of the Neuroimage Processing ToolKit (NPTK) on Neuroinformatics Tools and Resources Clearinghouse (NITRC) (http://www.nitrc.org).