Predicting Physical Interactions between Protein Complexes

Abstract

Protein complexes enact most biochemical functions in the cell. Dynamic interactions between protein complexes are frequent in many cellular processes. As they are often of a transient nature, they may be difficult to detect using current genome-wide screens. Here, we describe a method to computationally predict physical interactions between protein complexes, applied to both humans and yeast. We integrated manually curated protein complexes and physical protein interaction networks, and we designed a statistical method to identify pairs of protein complexes where the number of protein interactions between a complex pair is due to an actual physical interaction between the complexes. An evaluation against manually curated physical complex-complex interactions in yeast revealed that 50% of these interactions could be predicted in this manner. A community network analysis of the highest scoring pairs revealed a biologically sensible organization of physical complex-complex interactions in the cell. Such analyses of proteomes may serve as a guide to the discovery of novel functional cellular relationships.

Protein complexes are central to nearly all biochemical processes in the cell (1). In physiologically relevant states, their protein members assemble with varying degrees of stability, over time and under different cellular conditions, to carry out specific cellular functions (1). Although it is a dynamic and tightly regulated process, there is much evidence to support the notion that protein complex assembly results in discrete signaling macromolecules (2). According to the modular organization of molecular networks of the cell (3), protein complexes cooperate in functional networks through dynamic physical interactions with other macromolecules, including other protein complexes (4–6). These physical interactions between pairs of protein complexes may form the backbone of cellular processes (7), such as the recruitment of complexes by other complexes to sites of genome reorganization or in signaling networks. In this study, we attempted to predict these physical interactions between all pairs of known protein complexes, using the manually curated protein complex databases in CORUM and CYC2008 for humans and yeast, respectively.

The physical protein interactions that may occur between pairs of complexes have been reported to be more transient, compared with the combination of both permanent and transient interactions that occur within complexes (8). Indeed, the very stability of protein interactions within a protein complex lies between the two extremes of either transient or permanent states (9). Consequently, the experimental identification in a genome-wide manner of the physical interactions between pairs of complexes is very difficult. This challenge has recently been addressed (7, 10) by experiments where the weak interactions were preserved during affinity purifications, followed by inference of the less stable interactions of proteins with the core proteins within the complex. Guided by a computational method to predict the list of protein members in the complexes (10), this allowed a screen of putative inter-complex relationships from human cell lines (7). This adds to the many landmark developments in recent years to characterize protein complexes in a genome-wide manner (7, 11–13). However, in these experiments it is not always easy to infer accurately what constitutes the protein members of a protein complex. Because of various experimental limitations (14) and the dynamic nature of complex assembly in the cell (15), the protein members of the complexes must be predicted from thousands of purification measurements (10–12, 16). As a result, there are surprisingly large differences in the protein complexes inferred in these studies, depending on the algorithm used (17, 18). Hence, the inference of protein complexes from genome-wide screens (11, 12) is likely to contain significant noise from false-positives resulting from methodological uncertainty (9). This noise would in turn cause ambiguity when attempting to predict, genome-wide, interactions that may occur between protein complexes. One solution to this problem, as applied in this study, is the use of comprehensive databases of the so-called “gold standard” community definitions of protein complexes (19–22). In these resources, critical reading of the scientific literature by trained experts leads to definitions of the lists of protein members that are experimentally verified to form complexes. Each of these manually curated protein complexes are assigned functional annotations and a unique identifier. It is our assumption that this approach will allow for a more accurate resolution of the physical interactions between protein complexes.

Based on this reasoning, we utilized all protein complex pairs from 1216 human protein complexes in CORUM (21) and 471 in the yeast CYC2008 databases (22, 23), and we attempted to predict physical interactions between them.

To this end, we integrated only binary physical protein interactions that were experimentally verified and supported by Medline references, from the iRefIndex database (24, 25), and we developed a statistical method that compared the number of observed physical protein interactions between pairs of protein complexes versus the number of protein interactions expected to be present in pairs of randomized protein complexes. The highest scoring predicted pairs formed a network that was analyzed to identify communities of physically interacting protein complexes. Such higher order perspectives of cellular proteomes may aid discovery of novel functional relationships and lead to an improved understanding of cellular behavior.

One recent study utilized manually curated protein complexes-complex interactions in yeast (23) as part of a machine learning strategy to identify complex-complex interactions. However, they added to the training data complex pairs enriched with protein interactions under the assumption that these were likely to contain complex-complex interactions but without a clear statistical argument to assess the reliability of these. Our aim has been to provide a more rigorous statistical approach applied to yeast and human, in which the main confounding factors, protein degrees and protein similarities within the complexes, have been taken into account.

We used only the manually curated yeast complex-complex interactions from Ref. 23 as the reference set to evaluate our method after verifying with the authors that the manual curation had not been guided by enrichment in the protein network. Of these interactions, we predicted half at a 10% false discovery rate. Thus, although improvements in data as well as methods are still required for a more complete prediction of complex-complex interactions, a fair portion of these interactions can be reliably predicted now by using our method.

MATERIALS AND METHODS

Sources of the Physical Protein Interaction Networks

The binary physical protein interactions for both humans and yeast were downloaded from the on-line iRefWeb site (25). There, protein interactions are sourced from 10 integrated protein interaction databases. The protein interactions, their annotations, and their identifiers are integrated in this resource using the iRefIndex method (24). Briefly, this integration method maps protein identifications across the 10 databases, enabling systematic backtracking to establish the nonredundant identity of the interaction partners. A strict filtering process for each protein interaction was applied whereby we selected only physical binary protein interactions from the iRefWeb that had all of the following criteria: (a) experimentally verified; (b) within the same organism; (c) at least one supporting publication in Medline, and (d) physically binding protein interactions. The final protein interaction network used and the network used after exclusion of the intra-complex protein interactions can be found in supplemental Tables 7 and 8, for humans and yeast, respectively. The high confidence protein networks for humans were sourced from the databases HIPPIE (26) and HitPredict (27).

Sources of Manually Curated Protein Complexes

The human complexes were downloaded from the CORUM database (see supplemental Tables 7 and 8, for humans and yeast, respectively) (21). This is the largest repository of mammalian manually curated protein complexes. Only protein complexes that have been isolated and characterized by reliable experimental evidence are included. In CORUM, a protein complex has to be isolated as one molecule and must not be a construct derived from several experiments. In addition, artificial constructs of subcomplexes are not taken into account. Because of information from high throughput experiments containing a significant fraction of false-positive results, this source of data is excluded in their curation process. Medline references supporting a protein complex are mainly from articles judged to have placed importance on the characterization of protein complexes.

The manually curated yeast complexes were from a study that characterized both predicted and curated complexes (23), from which we only used their 87 manually curated complexes. These curated complexes were merged with the comprehensive CYC2008 database of curated yeast complexes (7). This is a catalogue is of 408 manually curated yeast complexes derived from small scale studies. It is reported to be a resource that represents a complete and up-to-date description of the stable yeast interactome (22).

Statistical Method and the Random Protein Complex Model

The complex-complex degree between a pair of complexes was defined as the number of interactions between pairs of proteins pairs, one from each complex, and was computed for all pairs of protein complexes. We then computed the expected complex-complex degree, λ, under a random model where we permuted the protein membership of the complexes but preserve the complex sizes (number of protein members of a complex) and protein degrees (number of physical protein interactions for the protein). Because large complexes containing high degree proteins are more likely to correspond to protein interactions by chance alone, leading to an over-prediction for such complexes and under-prediction for small complexes or complexes with low degree proteins, we considered controlling for size and degree as important.

We binned the proteins based on their degree in the protein network, and we permuted the proteins within each bin. To ensure sufficient numbers of proteins within each bin to allow for sufficient permutation of the proteins, some protein degrees were binned together as follows: degrees 0–39 were separate bins, from 40 to 59 bins were intervals of length 2 (i.e. 40–41 and 42–43), from 60 to 79 of length 5, from 80 to 119 of length 10, from 120 to 199 of length 20, from 200 to 299 of length 50, and degree 300 and above were put into bins of length 100.

The probability that two random proteins of degree D₁ and D₂ interact is shown in Equation 1,

and if D₁ and D₂ are different, see Equation 2,

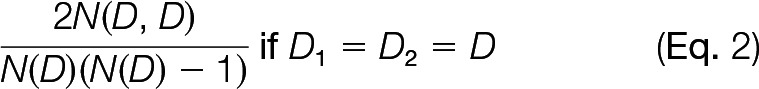where N(D) is the number of proteins of degree D (or in the D-bin when the degree is 40 or above) in the network, and N(D₁,D₂) is the number of edges between a degree D₁ and a degree D₂ (or their respective bins). The expected number of random interactions was then computed by summing this probability over all pairs of proteins for each complex pair.

The deviance residual, R(χ;λ), of the actual complex-complex degree, χ, relative to a Poisson distribution with the expected number of random interactions, λ, was then computed as shown in Equation 3,

where

Ideally, the residuals R(χ;λ) should behave approximately like a standard normal distribution. Of course, because χ takes integer values, this will be a very rough approximation for low values, but for the larger values of χ and large ratios of χ/λ it may still be expected to give fair p values. One might argue that a binomial or hypergeometric model could have been more appropriate than a Poisson assumption, but as long as χ is much less than the degree of each of the complexes, there was likely to be very little difference, although if χ is close to the complex degrees (which are upper bounds on χ) the Poisson assumption may be somewhat conservative in this approach.

Overdispersion Correction for Shared Protein Interaction Partners within Complexes

The Poisson assumption assumes that different interactions occur independently. However, if multiple proteins within a complex are known a priori to have the same interaction partners, these interactions are not independent. We corrected for this source of overdispersion by dividing the deviance D(χ;λ) by a factor φ, as shown in Equation 4,

where d₁ and d₂ represent the numbers of shared interaction partners for pairs of proteins summed over all pairs of protein in each of the two complexes, and D is the degree of the complex. The deviance residual is corrected by dividing by √φ.

There are several motivations for adding the term d/D to the overdispersion for each of the complexes (although they do not constitute full statistical models with conservation of protein degrees). For example, assume that for a given complex, there are exactly m_k proteins in the protein interaction network (and not in the complex itself) that interact with exactly k proteins within the complex. Randomizing the proteins outside the complex, each of the interaction partners has likelihood, p, of belonging to the other complex. Thus, for X the random number of complex-complex interactions, the expected value and variance becomes Equation 5,

and

where D = Σ_{k ≥1}m_kK is the degree of the complex, and V₀ = p(1 − p)D is the variance, without taking shared interaction partners into account. In our actual analyses, we have used V₀ ≈ E(X) as an approximation, which is appropriate if p is small.

The justification for applying the correction factor was evident from our observation that the variance of the deviance residuals, R(χ;λ), was higher than expected and increased with increasing overdispersion estimates. After correction for overdispersion, these problems were less apparent.

Community Detection from Predicted Complex-Complex Networks

To detect network communities of physical complex-complex interactions, we applied the algorithm outlined by Ahn et al. (28). This was applied to a network where each complex-complex prediction was reliable for either of the rules (<10% FDR,¹ with either ICE or BSO rules). In brief, the method uses the Jaccard coefficient for assigning similarity between two complex-complex interactions, e_ik and e_ik, which share a protein complex, node k, as shown in Equation 6,

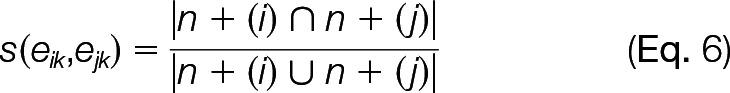where n + (i) refers to the first-order node neighborhood of node i. After assigning pairwise similarities to all of the links in the complex-complex network, the links are hierarchically clustered, using single linkage. The resulting dendrogram was cut at a point that maximizes the density of links within the clusters, normalizing against the maximum and minimum numbers of links possible in each cluster, known as the partition density (fully described in Ahn et al. (28)). Hierarchical clustering was carried out on the resulting 90 communities, using the Jaccard coefficient as a measure of the numbers of nodes shared by pairs of communities to find the meta-communities.

RESULTS

Framework to Predict Physical Complex-Complex Interactions

A flow chart of the method to predict physical interactions between protein complexes is illustrated in Fig. 1. In this method, for each pair of manually curated protein complexes, we counted the number of physical protein interactions between their proteins, which we refer to as the complex-complex degree. We interpret high complex-complex degree as an indication that there is an interaction between the complexes. High complex-complex degree indicates that there are several protein pairs that are able to form a bond between the two complexes, and thus the complexes are more likely to interact. An alternative motivation is that many of the physical protein interactions may be detected because of physical complex-complex interactions in which they partake. Although these two motivations are somewhat complementary, they imply different treatment of physically interacting protein pairs that may form intra-complex interactions, i.e. interact within a complex. There are usually multiple interactions within each complex, and unless appropriately handled these could induce spurious predictions of interactions between complexes.

Fig. 1.

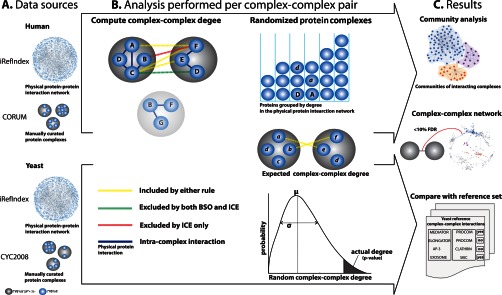
Flowchart. A, data sources. We downloaded validated networks of physical protein interactions from iRefIndex and curated lists of protein complexes from Corum (human) and CYC2008 (yeast). Data from humans and yeast were analyzed separately but using the same techniques. B, analysis was performed for each pair of complexes. First, we computed the complex-complex degree for each pair of complexes and then identified all interactions in the protein network between proteins in the two complexes. The complex-complex degree refers to the number of such interactions. We applied two different rules to exclude proteins and interactions that could induce spurious predictions. In the binding site occupancy rule (BSO), proteins found in both complexes (e.g. protein D in the example) were excluded, and only protein interactions between the remaining interactions were counted (leaving four interactions in the example). The motivation was that an interaction involving shared proteins, e.g. the C-D interaction in the example, is more likely to form within the complex than between the complexes. The intra-complex exclusion rule (ICE), in addition to excluding shared proteins, also excluded interactions between proteins if these coexist in some other complex (e.g. the B-F interaction in the example, leaving three interactions to be counted). The motivation for the ICE rule is to enrich the interaction network with inter-complex interactions. Separate analyses were performed using the BSO and ICE rules. Next, we carried out randomization of the protein complexes. To assess if a complex pair had a complex-complex degree higher than expected by chance alone, we computed the expected complex-complex degree for randomized protein complexes. The randomization consisted of replacing each protein in the two complexes with random proteins of the same (or similar) degrees. In addition to computing the expected complex-complex degree, we estimated the standard deviation taking into account similarities between proteins within complexes, i.e. proteins sharing many of the same interaction partners. p values were then computed based on an over-dispersed Poisson distribution, and false discovery rates were computed from these. C, results of the method. For prediction in both human and yeast, and for both the BSO and the ICE rules, we generated a list of predicted complex-complex interactions with FDR = <10%. In yeast, we compared our predictions to a list of 67 curated complex-complex interactions.

The BSO rule dictated that two proteins could not simultaneously interact within a complex and between complexes. Thus, if two complexes contain a common protein, we assumed that any protein interacting with this is more likely to do so within the same complex and thus should not be used as evidence of a physical interaction between the complexes. Effectively, for any pair of complexes, this corresponds to excluding any proteins they have in common prior to counting the complex-complex degree.

The ICE rule was stricter in that, prior to all analyses, it excluded from the physical protein interaction network all interactions between proteins found within the same complex. By removing interactions that are likely to be intra-complex interactions, the remaining physical protein interaction network should be enriched with interactions formed between complexes.

For both humans and yeast, analyses were performed once with the BSO rule and once with the ICE rule. If two complexes share a set of proteins, either rule prevents interactions involving these common proteins from influencing the predictions. However, in particular for human, we found a number of cases where, from a moderate number of proteins, several different complexes could form with varying sets of overlapping proteins. When this is the case, many of the protein-protein interactions excluded by the ICE rule remained when applying only the BSO rule, and the two methods differed significantly.

Predicted Physical Complex-Complex Interactions

In vivo, a physical complex-complex interaction may require no more than a single physical protein interaction between the two complexes. However, to reliably predict physical complex-complex interactions, we had to distinguish them from the thousands of arbitrary pairs of complexes, most of which do not interact. We did this by identifying pairs of complexes with complex-complex degrees higher than what would be expected from pairs of randomized protein complexes.

To determine the expected complex-complex degree, we considered randomized complexes in which the proteins of the physical protein interaction network had been permuted, i.e. each protein was replaced by a randomly selected protein of the same degree (number of interaction partners in the physical protein interaction network) as the original one. For high degree proteins, we needed to bin together multiple degrees to get a sufficient number of proteins in each bin. Proteins found in both complexes were excluded as both exclusion rules prevent these from contributing to the complex-complex degree. From the random model, we computed the expected complex-complex degree for each pair of complexes, and we compared the actual complex-complex degree to the expected degree. As a measure of the difference, we used the deviance residual relative to a Poisson distribution. (see “Materials and Methods ” for further details.)

Ideally, we should be able to analyze the deviance residuals as if they were the standard normally distributed, i.e. expected value 0 and variance 1. The majority of protein complex pairs had no physical protein interactions between them, and therefore should abide by this assumption. However, we observed that many complexes contained proteins that were similar in the sense that they had many of the same interaction partners in the physical protein interaction network. One reason for this is co-occurrence of homologous proteins in the same protein complex (see supplemental Fig. S1, A and B, for effects of merging paralogous proteins with 50% identity) (29). However, we found this similarity to be far more widespread than could be explained by homology, and so we needed to adjust for this in a more general manner. Although co-occurrence of similar proteins does not affect the expected complex-complex degree, it does cause overdispersion, i.e. an increase in the variance of the distribution. We corrected the deviance residual scores by dividing the scores by an overdispersion correction factor estimated for each complex pair from the number of shared physical interaction partners between proteins in each of the two complexes (see under “Materials and Methods”). The deviance residual scores adjusted for overdispersion are illustrated for human physical complex-complex interactions in Fig. 2A for the BSO rule (the plots for both humans and yeast, applied using both rules, are illustrated in supplemental Fig. S1, A–G). From the deviance residuals corrected for overdispersion, we computed p values, and from these the FDR. With a threshold of 10% FDR, we predicted 375 and 428 physical complex-complex interactions for the ICE rule in humans and yeast, respectively. For the BSO rule, there were 1216 and 188 predictions for humans and yeast, respectively. Summary statistics of the source data and predictions are presented in supplemental Table 1. The predicted physical complex-complex interactions for both rules and organisms at 10% FDR can be seen in supplemental Table 2.

Fig. 2.

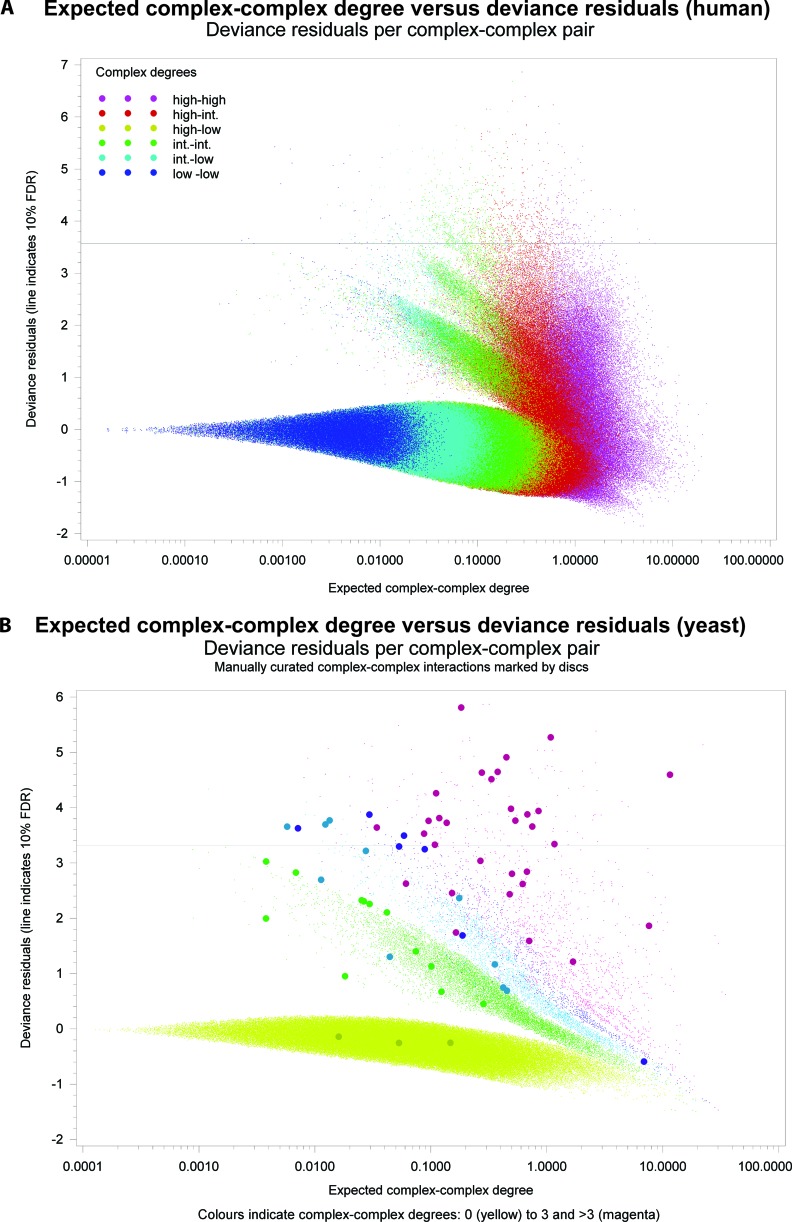
A, plot of deviance residuals (y axes) against the expected complex-complex degree (x axes) for all complex-complex pairs in humans with the BSO rule applied. Each data point represents a complex-complex pair, with overlapping points spread out to better illustrate the number of cases. The complex-complex predictions having an FDR of <10% are indicated above the gray line. Each data point is classified and color-coded according to the total complex degree (sum of the protein network degrees over all members of the complex). It is apparent that an intrinsic high protein network degree of a complex does not systematically bias the predictions. B shows the distribution of the expected random complex-complex degree against the deviance residuals in yeast (BSO rule). The data points in this plot are color-coded according to their actual complex-complex degree. The yeast manually curated interactions from (23), are visible as larger circles.

Complex-complex pairs with high deviance residuals, indicating higher complex-complex degrees than expected by chance, were found evenly across high and low degree complexes and were not particularly prone to coincide with high degree complexes or complexes with high degree proteins (Fig. 2A, supplemental Fig. S2, A–C for complex pairs categorized by total complex degree, and supplemental Fig. S2, D–G for average protein degree within complexes). However, as expected, for pairs of low degree complexes, protein interactions were rare, and the power to detect interactions between such complexes was low.

To further assess the validity of our analyses, we performed identical analyses on complexes where the proteins were actually randomized. This confirmed the assumption that random complex-complex degrees were approximately Poisson distributed and that the use of deviance residuals was appropriate, although slightly conservative, but it indicated that the correction for overdispersion made statistical tests very conservative (supplemental Figs. S3 and S4). However, as co-occurrence of similar proteins is far more common in actual complexes than in randomized complexes, the correction for overdispersion cannot be ignored.

The difference between the ICE rule and the BSO rule was largely due to two effects. In both organisms, the ICE rule removed a large number of interactions from the physical protein interaction network on the grounds that they may be intra-complex interactions, and we therefore lacked evidence that they interact between complexes. This reduced the protein degrees, i.e. number of interaction partners in the protein interaction network. The expected complex-complex degree for random complexes is based on the protein degrees, and lower protein degrees result in lowering the expected complex-complex degree for randomized complexes, making complex-complex interactions mediated by nonintra-complex interactions more easily detected. In yeast, the reduction in the expected complex-complex degree when applying the ICE rule was the dominant effect, resulting in higher sensitivity and more predicted complex-complex interactions under the ICE rule than under the BSO rule.

Conversely, in humans we saw several large clusters of partially overlapping complexes, and not merely complexes sharing a common set of core proteins, but groups of complexes where different pairs of complexes share different sets of genes. Under the BSO rule, a substantial portion of the predicted physical complex-complex interactions in humans were from such clusters, where the protein interactions that induced the predictions were intra-complex interactions from within other complexes in the same cluster. Although the complexes within such clusters appeared to be related, we have reservations against using these intra-complex interactions to infer physical interactions between the complexes. Because the ICE rule excluded all intra-complex interactions, it eliminated this problem, possibly making the ICE rule more reliable. The ICE rule, however, also appeared less powerful in humans (see supplemental Table 1), and it possibly missed many biologically relevant physical complex-complex interactions.

Evaluation of the Physical Complex-Complex Interaction Predictions

We evaluated the method on a set of 87 manually curated yeast complexes, used in machine learning by Wang et al. (23). These interactions were sent to us by request from the authors, along with a confirmation that they were not selected for having an enriched number of protein interactions between them. There were 59 such interactions between 81 complexes used in that study (23). These 81 complexes were a subset of 87 initial complexes forming the 67 curated interactions, after the authors applied filtering to merge them into their interaction network (written communication from the authors). There was an additional 66 interactions added to the training data by Wang et al. (23), selected based on enrichment of protein interactions between their members. This enrichment is a property similar to our computation of the complex-complex degree. To avoid circular reasoning, these enriched interactions were therefore not used in our evaluation. The 87 manually curated protein complexes that form these 67 reference interactions were combined with the 408 manually curated yeast complexes from CYC2008 (22). When applying the method using the ICE rule on this set, we predicted 33 of the 67 reference interactions at a 10% FDR threshold, and with the BSO rule we predicted 26 (22 of the reference physical complex-complex interactions were common to both rules, see supplemental Table 3 and Fig. 2B).

These 67 expertly curated interactions were the only gold standard resources available in yeast, and there are no existing catalogues of curated physical complex-complex interactions in humans that could be used for similar evaluation purposes. However, for protein complex pairs to interact, they must be simultaneously expressed in the same cellular specific conditions. We therefore assessed the validity of the predicted physical complex-complex interactions from a human tissue-specific perspective. We applied the method on tissue-specific expression patterns from 79 human tissues (30) and their inferred tissue-specific protein-protein interaction networks (31) in the context of the human curated protein complexes in CORUM. For ∼26% of the 1216 human complexes, we could not identify any tissue in which at least 80% of its member proteins were expressed. Of the initial 375 predicted complex-complex interactions (ICE rule, FDR <10%), this left 228 in which each complex had at least one identified tissue. Of these, 201 (88%) were co-expressed in the same tissue. On average, the predicted interactions were found co-expressed in 2.5 tissues, with none co-expressed in more than 80% of the tissues. Co-expression is a requirement for physical interactions to occur between protein complexes and may be seen as validation of the predictions. However, this should be considered with caution because interacting proteins need to be co-expressed, and the co-expression of complexes may in part be the results of selecting pairs of complexes containing several co-expressed proteins.

The predictions described here were generated using protein interactions subject to strict filtering (see “Materials and Methods”). To evaluate the reliability of these sources, we assessed the performance of the method against two different databases of high confidence protein interactions (26, 27). As these high confidence protein networks were smaller, the power of the method decreased as could be expected, resulting in fewer predictions (see supplemental Table 4). However, in a comparison of the results using these high confidence interactions against random subsets of protein interactions of similar size, it appeared that there was no substantial difference in the performance (see supplemental Table 4).

Biologically Relevant Human Physical Complex-Complex Interactions

Inspection of the predictions from the more stringent ICE rule in the human physical complex-complex network identified biologically relevant relationships. For example, the highest scores revealed archetypal cooperation between mediator complexes interacting with RNA polymerase, linking co-activators to the general transcriptional machinery (supplemental Table 2). In particular, the highest scoring interaction in humans points to a direct relationship between a BRCA1-bound RNA-polymerase II complex (32) and a mediator complex (33), possibly allowing for the subsequent transcriptional activation of the RNA polymerase II.

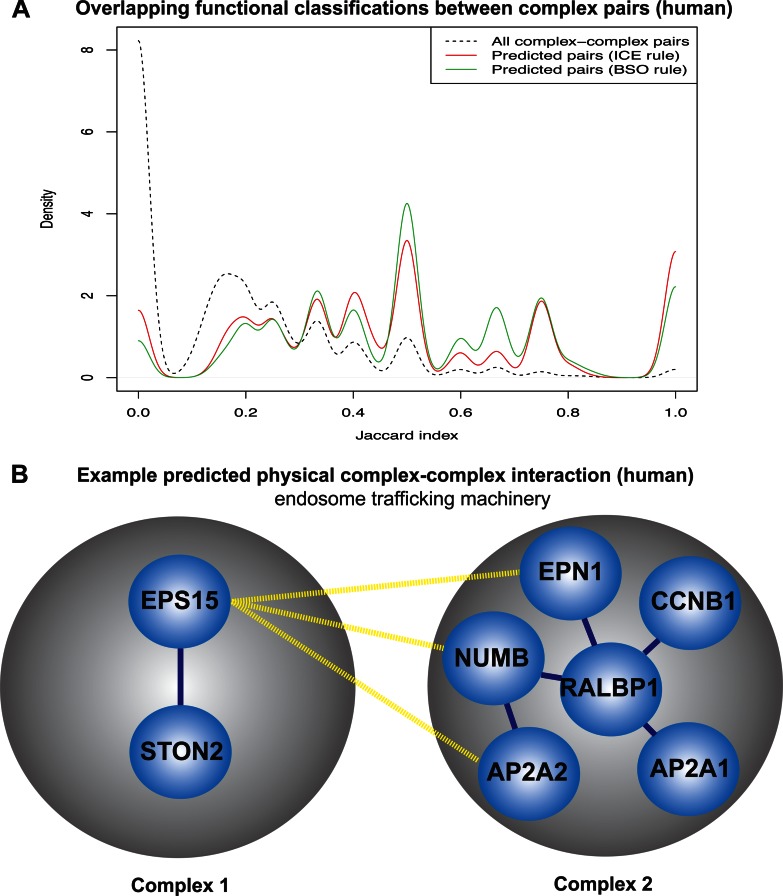
To examine the biological relevance from a more global perspective, we tested whether the overlapping Functional Catalogue (FunCat) annotations (34), manually assigned to each CORUM (21) complex, were more frequently higher among predicted pairs. We scored the complex pairs for overlapping FunCat annotations using the Jaccard Index (intersection divided by union). The resulting density plot is illustrated in Fig. 3A. The proportion of complex pairs having a Jaccard index of >0.5 was 33% for the ICE rule and 37% for the BSO rule, compared with 5% for all human complex pairs. This global perspective suggests that the predicted complex-complex pairs are more functionally related compared with the entire set of complex pairs in humans.

Fig. 3.

Biological relevance of the human physical complex-complex interactions. A, global illustration of biological relevance. The figure shows the density plot of the overlapping FunCat annotations among all complex pairs (dashed line), ICE rule predictions (red line), and the BSO rule predictions (green line). Here, we used the FunCat (34) annotations assigned manually to each individual complex from the CORUM database (21). The overlapping annotations for the complex pairs were scored using the Jaccard index, whereby the parent classification for each FunCat term is counted only once for each complex. B, specific example of a high scoring prediction of a physical complex-complex interaction. Complex 1 is a clathrin-mediated endosome complex (37), important for the internalization of receptors during cell signaling. The prediction is suggestive of a regulatory interaction with Complex 2, which is responsible for regulating the switching off of endosome trafficking during mitosis (36).

To investigate the biological relevance of a specific example, we selected an interaction predicted between two complexes of fairly common sizes and degrees and were not directly related, i.e. no protein member in common. The resulting example is one suggestive of the endosome regulatory machinery interacting with a trafficking complex during cell division (see Fig. 3B). Mitosis is a period of cell division where endocytosis is switched off (35) and the RLIP76-RalBP1 complex (Complex 2 in Fig. 3B) is related to an absence of endocytosis during mitosis (36). It has been proposed that the RLIP76-RalBP1 complex serves as a scaffold that brings together networks of endosome trafficking proteins to regulate endocytosis during the transition to mitosis during the cell cycle (36). The predicted complex interaction partner of the RLIP76-RalBP1 complex, Eps15-Stonin2 (Complex 1 in Fig. 3B), coordinates the internalization by clathrin-mediated endocytosis of receptors during signaling (37). Thus suggesting that this predicted physical complex-complex interaction might have a regulatory role on endosome mediated signaling during the cell cycle, and therefore a candidate for experimental validation.

Higher Order Organization of Physical Complex-Complex Interactions

To examine the cellular organization of the predictions from a global network perspective, we defined a physical complex-complex interaction network in humans, where the interactions are significant with either rule (<10% FDR). Either rule was chosen because although the ICE rule is more reliable due to strict exclusion of protein interactions occurring at least once within any protein complex, in reality, however, many protein interactions occur within and between complexes in different dynamic contexts. The resulting network consisted of 1365 predicted interactions between 540 complexes (see Fig. 4A). We then applied an edge-based community detection algorithm (28) to identify functional groups of physical complex-complex interactions that correspond to various cellular processes (see “Materials and Methods”). This community network analysis revealed a sensible biological organization of the cellular proteome into relevant physically interacting protein complex communities. There were in total 96 distinct communities identified (Fig. 4B), where there were clear functional relationships between the complexes within each community, and many distinct communities could be detected. Examples of such were communities of physically interacting transcription factor complexes, cell-cell adhesion complexes, cell signaling, and genome organization machinery, etc. (see supplemental Table 5).

Fig. 4.

Multiscale and biologically sensible cellular organization of the human physical complex-complex interaction network. A, network of the highest scoring interactions at FDR <10% for either the BSO or ICE rules. Three of the meta-communities are color-coded in the network corresponding to their colors in the dendrogram in Fig 3C. B, hierarchical clustering dendrogram showing 15 clusters of physical complex-complex interactions (meta-communities). Each color represents a meta-community, and each line represents one of the 96 communities of physical complex-complex interactions. C, subnetwork of the human physical complex-complex interaction network where three meta-communities are colored accordingly. Using Gene Ontology (process tree) analysis, the genes mapped in these meta-communities depict examples of three distinct biological processes.

This community detection of physical complex-complex interactions allowed for a further so-called “multiscale” exploration of cellular organization by studying the similarity between the communities. The pairwise similarity between each community (number of shared complexes per community) was scored using the Jaccard Coefficient and was subsequently hierarchically clustered (see “Materials and Methods”). Such clustering between the 96 different communities produced 15 meta-communities (for the ICE rule alone it was 38 and 9, respectively). The functional class of these meta-communities was tested using the nonredundant list of proteins from each meta-community in a gene ontology (GO) analysis (gene set enrichment tests). GO functional classification of the complex-complex communities is illustrated in the dendrogram in Fig. 4B, and a subnetwork of three meta-communities is illustrated in Fig. 4C (complete lists, including that of the ICE rule alone, in supplemental Table 5). These groupings demonstrate an organized structure of the proteome across multiple scales, where the communities of physically interacting protein complexes correspond to a functional organization of the cell.

DISCUSSION

Capturing a higher order perspective of the complex molecular networks in a cell has been demonstrated previously to offer valuable new insights (38). It has also been suggested that cells could be interpreted as higher order networks of protein molecular machines, transforming and passing information to each other (5). In turn, it has been proposed that these discrete, yet dynamic, protein complexes form the backbone of cell regulation (2). One genome-wide study estimated there to be ∼3000 protein complexes in humans and ∼800 in yeast (11) involved in all processes of cellular life. Here, we took 1216 and 471 manually curated protein complexes in humans (21) and yeast (22, 23), respectively, and we attempted to predict the physical interactions between these molecular entities.

In the absence of having the three-dimensional structures for all the protein complexes, it was unknown which binding sites are available for interaction with proteins in other assembled complexes. The ICE and BSO protein exclusion rules were devised to consider the availability of binding sites between potential physical complex-complex interactions. These exclusion rules had a strong impact on predictions, despite excluding only a small percentage of the physical protein interactions, as they primarily took effect under rather specific conditions. The differences in the behavior of both rules within and between humans and yeast can be attributed to the observation of protein complex members overlapping much less in the yeast protein complexes than in human. The subsequent permutation and statistical analysis resulted in predictions of physically interacting complex-complex networks that corresponded to a sensible functional organization of the cell, as observed by the network community analysis

Evaluating the predictions in yeast, we found that approximately half of the physical complex-complex interactions could be predicted in this manner. However, the method is limited to detecting protein complex pairs that have multiple possible protein interactions between them. In addition, many physically interacting complex pairs were possibly not detected, which is likely due to the current incompleteness of the manually curated protein complex and protein interaction databases.

It was the goal of this study to predict physical interactions between two protein complexes, in an attempt to identify complex pairs that coordinate with each other to execute a cellular process. These interactions are likely to be transient and dependent on certain biochemical conditions at a specific time and cellular location. However, some of the predictions may not be transient physical interactions between two complexes, perhaps pointing to the assembly of larger stable complexes. The incomplete annotation in the curated databases means the larger assembly would not yet be considered as a unique entity and therefore results in an incorrect classification by the prediction method. These false-positives can be identified and resolved in future iterations of the method and improved by increased manual curation and more accurate experimental detection of intact protein complexes.

Another class of inter-complex relationships has been comprehensively mapped in so-called “complexome” studies, which have constructed networks of protein complexes, containing shared protein members (39–43). In those primarily yeast studies, two experimentally detected or predicted complexes are connected if they shared one or more protein members. These studies have revealed key insights into the pattern of protein complex organization in the cell. They can be considered different from the approach taken in this study, which focused on predicting physical interactions between protein complexes by identifying the complex pairs that are significantly enriched for physical protein interactions between them. With respect to this goal, one yeast study by Wang et al. (23) used a machine learning approach to detect signatures of complex-complex interactions. That particular study used a combination of manually curated complex-complex interactions and complex pairs enriched with reliable protein interactions between their members to train their model. However, these “enriched” complex pairs were used to augment their training data and, unlike this study, were not a result of statistical predictions under a complete randomized model (see under “Materials and Methods”). The cross-validation reported in that study was carried out using a merged reference set of enriched and curated complex-complex interactions. This is not directly comparable with our results, as the enriched interactions are selected based on our computation of the complex-complex degree. To avoid circular reasoning in our evaluation, we used only the manually curated complex pairs from the study by Wang et al. (23). When our method was applied to their enriched and predicted complex pairs, some major differences were clearly due to factors that we correct for, in particular the protein degree of the complexes (see supplemental Table 6). Another yeast study used logistic regression trained on nine different experimental and computational parameters of interacting and noninteracting protein pairs to infer interactions between stable protein interactions within complexes and transient interactions between complexes (8). There also has been a study in yeast to predict transient interactions between predicted protein complexes, based on similarity of protein members from pulldown assays (44). To the best of our knowledge, there were no previous attempts to predict physical complex-complex interactions restricted to manually curated protein complexes in human.

As more complete proteomes with characterized protein complexes (7) and their three-dimensional structures are fast approaching (45), the in silico mapping of the physically interacting relationships between protein complexes will be of greater importance. Genome-wide technologies are now evolving to capture these physical complex-complex interactions (45). The method described in this study could be used as a complementary tool in proteomics experiments, guiding the discovery of higher order interactions between protein complexes. For example, the application of this method, integrated with clustering algorithms that attempt to identify protein complexes from large protein networks (46), may guide the identification of higher order relationships in proteomics data (the SAS code is freely available by request from the authors). The prediction of complex-complex interactions will complement experimental advances and overall contribute to building complete molecular maps of the cell.