Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Jun 10.
Published in final edited form as: Behav Processes. 2009 Dec 14;83(2):191–196. doi: 10.1016/j.beproc.2009.12.009

Context affects the numerical semantic congruity effect in rhesus monkeys (Macaca mulatta)

Sarah M Jones *, Jessica F Cantlon #, Dustin J Merritt *, Elizabeth M Brannon *
PMCID: PMC3677752  NIHMSID: NIHMS460994  PMID: 20015467

Abstract

Do monkeys anchor their numerical judgments based on the context in which their choices are presented? We addressed this question by varying the numerical range across sessions while macaque monkeys made ordinal judgments. Monkeys were trained to make a conditional discrimination whereby they were reinforced for ordering arrays of dots in ascending or descending numerical order, dependent on a color cue. Monkeys were tested using two ranges of numerosities that converged on a single pair. Similar to the findings of Cantlon & Brannon (2005), we found a semantic congruity effect whereby decision time was systematically influenced by the congruity between the cue (ascending or descending) and the relative numerical magnitude of the stimuli within each range. Furthermore, monkeys showed a context effect, such that decision time for a given pair was dependent on whether it was a relatively small or large set of values compared to the other values presented in that session. This finding suggests that similar to humans, the semantic congruity effect observed in monkeys is anchored by the context. Thus our data provide further evidence for the existence of a shared numerical comparison process in monkeys and humans.

Keywords: nonhuman primates, numerical cognition

Introduction

There is abundant evidence that approximate numerical representations are universal in human societies, appear early in human development and are shared by nonhuman animals (see Brannon, 2005; 2006; Feigenson, et al, 2004; Neider & Miller, 2004 for reviews). In all of these groups, approximate number discrimination appears to be governed by Weber's law such that accuracy decreases and reaction time increases for numerical comparisons as the ratio between the two values (min/max) approaches 1. For adult humans, Weber’s law holds across many numerical formats such as spoken words, Arabic numerals, tones, and dot arrays (Dehaene & Akhavein, 1995; Pica, et al., 2004; Whalen, et al, 1999; Dehaene, et al, 2008).

A lesser known characteristic of adult human numerical comparisons is the semantic congruity effect. When asked to compare two large items, adults are quicker to respond to the question “Which is larger?” than “Which is smaller?” Conversely, when asked to compare two small items, adults are quicker to respond to the question “Which is smaller?” than “Which is larger?” The semantic congruity effect has been demonstrated with a variety of stimuli, including animal sizes, distance between cities, line length, brightness, surface area, Arabic numerals, and the numerosity of dot arrays (Cech & Shoben, 1985; Cech, et al, 1990; Holyoak & Mah, 1982; Petrusic, et al, 1998; Audley & Wallis, 1964; Moyer & Bayer, 1976; Banks, et al. 1976; Holyoak, 1978). For example, when evaluating Arabic numerals, adults indicate that 2 is smaller than 3 more quickly than they indicate that 3 is larger than 2. However, when presented with two relatively large values such as 8 and 9, adults are faster when asked to indicate the larger compared to the smaller value (Banks, et al. 1976).

One proposal that accounts for the semantic congruity effect is the propositionally based semantic theory also known as the Discrete Code model (Banks, 1977; Banks, et al, 1975; Banks, et al. 1976; Cech, et al. 1990.) According to this model, when two stimuli are compared on the basis of size or number, they are coded for magnitude (Small or Large) using symbolic or linguistic processes. When the stimuli being compared differ greatly in magnitude, they are given different magnitude codes (e.g. small vs. large). If asked “which is larger?” or “which is smaller?”, these codes can then be quickly and easily matched to the form of the question. However, when the stimuli being compared are either both large or both small, then the magnitude codes for both stimuli will be similar to one another (e.g. Large and Large+ or Small and Small+, respectively). If both stimuli have similar magnitude codes, and the form of the question does not match those codes, (i.e. when both stimuli are small, but the instruction is “choose larger”), then the codes must be translated from Small/Small+ to Small/Large so that one of the codes is consistent with the form of instruction. Under this proposal, the reaction-time patterns that characterize the semantic congruity effect are the result of the added processing time necessary to translate these codes.

In contrast to the idea that semantic congruity effects emerge from linguistic coding, Cantlon & Brannon (2005) demonstrated a numerical semantic congruity effect with a nonverbal species; the macaque monkey (Macaca mulatta). Monkeys were trained on a touch screen computer to choose between two arrays of dots. A color cue indicated whether they would be rewarded for selecting the array with the larger (blue background) or smaller (red background) number of dots. The monkeys were tested with pairs of dots that ranged in value from 1 – 9. Monkeys showed a semantic congruity effect similar to that reported for humans: with a red background, they were faster to respond that 2 was smaller than 3 than they were to respond that 3 was larger than 2. In contrast, when the values were relatively large (i.e. 7 vs. 8), monkeys were faster to indicate the larger of the two values than they were to indicate the smaller of the two values with a blue background. Evidence of the semantic congruity effect in a nonlinguistic animal species demonstrates that the effect must not depend on linguistic coding.

An alternative model, proposed by Holyoak and colleagues (Holyoak, 1978; Holyoak & Mah, 1982), does not rely on linguistic processes and instead assumes that humans compare stimuli with respect to a reference point which is either established implicitly by the form of the question or is presented explicitly by the experimenters. Holyoak (1978) tested his reference point model by presenting participants with an explicit reference point on a numerical continuum and asking them to determine which of two digits in the range 1–9 was closer to that reference point. When the reference point was set at 1 or 9, reaction times showed a clear congruity effect similar to that reported by Banks, et al. (1976). When the reference point was set at a value in the middle of the range of values presented, reaction time was fastest for the pairs closest to the reference point provided.

The reference point model suggests that the endpoints of the continuum being tested serve as temporary reference points, and therefore, reaction-time patterns for a given pair are dependent on whether the pair is considered to be relatively small or large within the range of values being tested. Thus, if a given pair of numerosities (or digits) were close to the higher endpoint of the testing range, then participants would be faster to choose the larger value in the pair (e.g., 8 vs. 9 in the range 1 to 9). If the range of values were then changed such that the same pair was closer to the lower endpoints, we would expect the subjects to be faster at indicating the smaller value of the pair (e.g., 8 vs. 9 in the range 8 to 64).

Cech & Shoben (1985) demonstrated this context effect for semantic congruity in adult humans. In their study, participants were presented with pairs of animals and asked which was larger or which was smaller. When only small animals were presented, participants were faster at choosing the larger of the two largest animals in that range (i.e. Rabbit-beaver), but when those same animals were presented in a broader range, the smaller of the two was identified more rapidly. Thus, the speed of human comparison judgments is determined in part by the range of choice options available (i.e., the context of the judgment).

Like the semantic congruity effect, the context effect is a signature of the mental comparison process that has been shown in human adults. If monkeys and humans are using a homologous mental comparison process, then the range effects shown by humans should also be evident in the reaction time patterns shown by monkeys making numerical comparisons. The goal of the current paper is to examine the role of context on the semantic congruity effect in the numerical judgments of nonhuman primates. If context affects numerical semantic congruity in nonhuman primates similar to humans, then the effect cannot be attributed to uniquely human processes such as linguistic encoding. Instead, it would provide further evidence of a shared comparison algorithm between humans and nonhuman primates.

Methods

Subjects and Apparatus

Subjects were 2 socially-housed adult female rhesus macaques (Macaca mulatta), Mikulski and Schroeder. Both monkeys were kept on a water-restricted diet approved by an institutional animal care and use committee. Subjects were tested in sound-attenuated booths while seated in Plexiglas primate chairs fitted with a water delivery system. Stimuli were presented on a touch screen computer monitor.

Task and Procedure

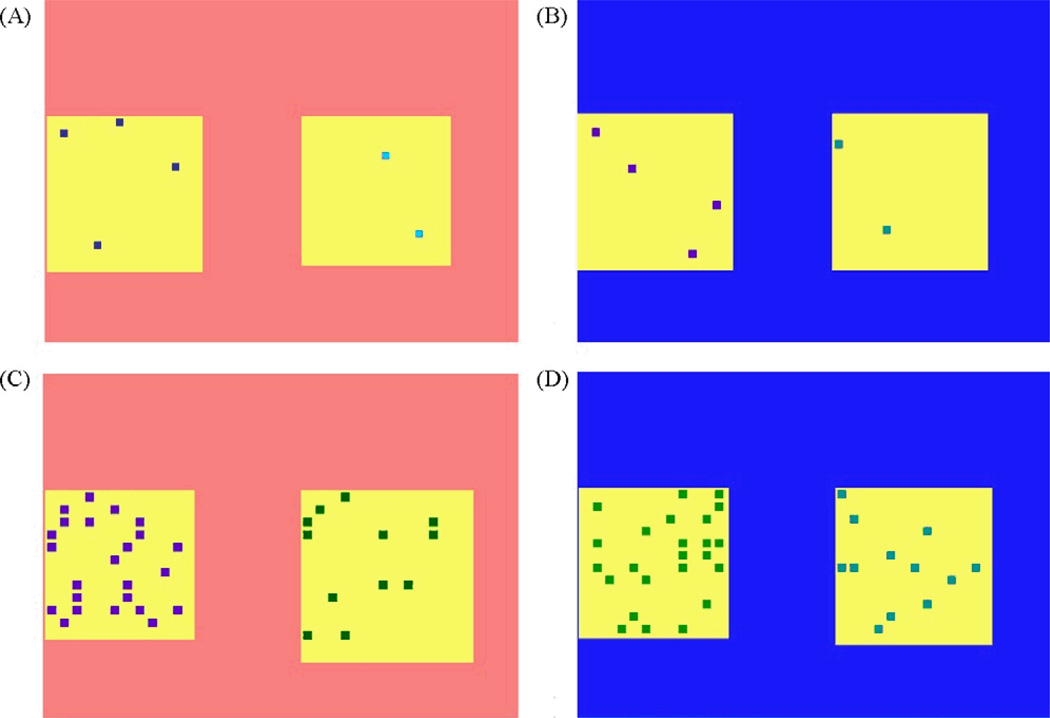
Subjects initiated each trial by touching a start stimulus, a small red square in the bottom-right corner of the screen. Pressing the start stimulus caused it to disappear, after which, two arrays of dots, each of which contained between 1 and 72 elements, were presented in random spatial locations (selected from one of four locations) on the screen. (Figure 1).

Figure 1.

Figure 1

Open in a new tab

(A) Example of an ascending trial in small range, (B) example of a descending trial in small range, (C) example of an ascending trial in large range, (D) example of a descending trial in large range. Note that the background screen color was red for all ascending trials and blue for all descending trials.

If the background color of the screen was red, subjects were rewarded for selecting the array with the smaller number of elements first (“ascending” trials). If the background was blue, reward was given for selecting the array with the larger number of elements first (“descending” trials). Ascending and descending trials were randomly intermixed within a session. A trial was terminated after the arrays were touched in the correct order, or when the subject made an incorrect response. Correct trials were rewarded with 1.16 ml of water and positive auditory feedback, which was followed by a 1 second intertrial interval (ITI). Incorrect responses ended the trial and initiated a 2 second time-out added to the intertrial interval (ITI) and negative auditory feedback.

Prior Training

Both monkeys had extensive prior numerical training, including numerical matching and ordinal tasks. Mikulski had experience ordering all pairs of 1–9, as well as larger numerosities up to 150. Schroeder had more limited prior training ordering pairs with a 1:2 ratio with absolute values between 1 and 150. Prior training for Mikulski is described in Cantlon and Brannon (2005) and training for Schroeder was similar.

Testing

Subjects were tested using the task described above for two ranges. The small range contained the following numerosity pairs: 1:2, 2:4, 3:6, 4:8, 5:10, 6:12. The large range was established by multiplying the small range by 6, thereby creating the pairs 6:12, 12:24, 18:36, 24:48, 30:60, 36:72. The two ranges were presented in blocks of 5 sessions1 in an ABBA design where A refers to the small range and B refers to the large range. Each session contained 200 trials.

Stimuli

Stimuli were randomly generated by a RealBasic program and were thus trial unique according to parameters that allowed surface area, element size and color to be controlled. All elements within a stimulus were square and the background of the array was always yellow. Individual elements were homogeneous in color within an array and the color was randomly selected for each stimulus from a list of 16 colors (brown, red, green, turquoise, pink, dark blue, orange, gray, blue, dark green, periwinkle, purple, teal, dark red, dark purple and dark pink.). Elements within each stimulus were also homogeneous in size and varied between .04 and 36 cm2. To control for cumulative surface area and individual element size, surface area was equated for the two arrays on half of the trials, whereas element size was equated for the two arrays on the other half of trials. To control for density, the density of the two arrays was congruent with number on half of the trials and was either equated for the two arrays or incongruent with number on the other half of the trials.

Results

Overall, monkeys performed significantly above chance across all test sessions on both the ascending trials [single-sample t tests vs. 50% (chance), Mikulski, mean accuracy 73%, t(19) =13.01, p < 0.001; Schroeder, mean accuracy 66%, t(19) =11.63, p < 0.001] and the descending trials [single-sample t tests: Mikulski, mean accuracy 70%, t(19) =15.48, p < 0.001; Schroeder, mean accuracy 63%, t(19) = 10.54, p < 0.001]. Performance did not differ between ascending and descending trials [Mikulski, t(19) =.74, p = 0.47; Schroeder, t(19) = 1.47, p = 0.16].

Monkeys performed significantly above chance both when density was congruent with number [single-sample t tests; Mikulski, t(19) = 27.72, p < 0.001; Schroeder, t(19) = 16.91, p < 0.001] and when density was not congruent with number2 [single sample t tests; Mikulski, t(19)= 20.69, p < 0.001; Schroeder, t(19) = 9.75, p < 0.001]. Similarly, monkeys performed significantly above chance both when cumulative surface area was congruent with number [single-sample t tests; Mikulski, t(19) = 27.24, p < 0.001; Schroeder, t(19) = 20.84, p < 0.001] and when cumulative surface area was equated between the two arrays [single sample t tests; Mikulski, t(19)= 15.71, p < 0.001; Schroeder, t(19) = 6.85, p < 0.001]. Thus, both monkeys used numerical value, rather than density or cumulative surface area, to compare stimuli.

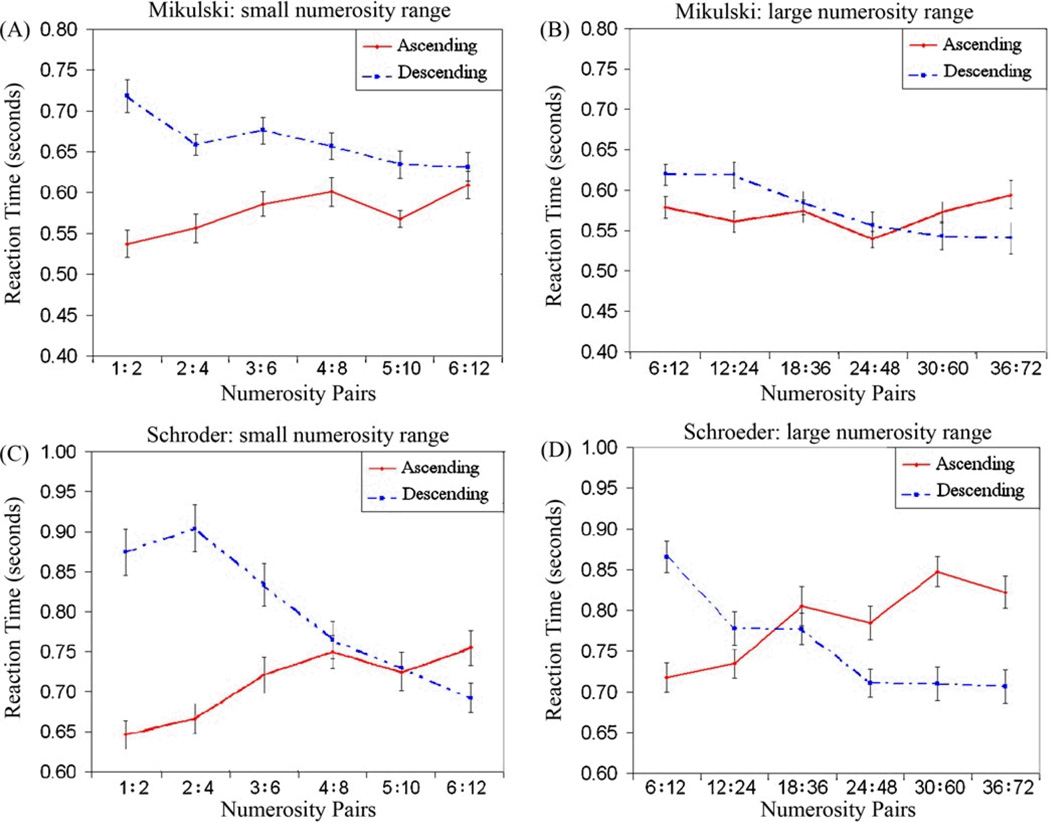
The main finding was that both monkeys showed a semantic congruity effect for the small and large numerosity ranges (Figure 2). In the small range, an ANOVA for Direction (ascending, descending) X Numerical Magnitude [Small (1 vs. 2, 2 vs. 4, 3 vs. 6), Large (4 vs. 8, 5 vs. 10, 6 vs. 12)] on RT revealed an interaction between the Direction and the Numerical Magnitude of the comparison stimuli for each monkey [Mikulski, F(3,39) = 29.34, p < 0.001; Schroeder, F(3,39) = 38.45, p < 0.001]. In addition there was a main effect of Direction for both monkeys [Mikulski, F(3,39) = 80.64, p < 0.001; Schroeder, F(3,39) = 14.88, p < 0.001], reflecting overall faster RTs on ascending trials than descending trials [Mikulski, t(19) = 6.07, p < 0.001; Schroeder, t(19) = 2.38, p < 0.05]. Finally there was a main effect of Numerical Magnitude for Schroeder [F(3,39) = 6.42, p < 0.05], reflecting moderately faster RTs on large pairs compared to small pairs in the small range [t(19) = 1.54, p =.14].

Figure 2.

Figure 2

Open in a new tab

(A) Mean RTs for Mikulski in small range, (B) Mean RTs for Mikulski in large range, (C) Mean RTs for Schroeder in small range, (D) Mean RTs for Schroeder in large range. Both monkeys showed a semantic congruity effect in both ranges.

In the large numerosity range, an ANOVA for Direction (ascending, descending) X Numerical Magnitude [Small (6 vs. 12, 12 vs. 24, 18 vs. 36), Large (24 vs. 48, 30 vs. 60, 36 vs. 72)] on RT also revealed an interaction between the Direction and the Numerical Magnitude of the comparison stimuli for both monkeys [Mikulski, F(3,39) = 21.11, p < 0.001; Schroeder, F(3,39) = 20.56, p < 0.001]. Thus, both monkeys showed a semantic congruity effect for both the small and large numerical ranges.

In addition to the interaction between direction and Numerical Magnitude in the large range there was a marginally significant main effect of Direction for Schroeder [F(3,39) = 3.80, p = 0.06], indicating overall faster RTs on descending than ascending trials. Finally there was a main effect of Numerical Magnitude for Mikulski [F(3,39) = 17.85, p < 0.001], reflecting overall faster RTs on small pairs than large pairs in this range [t(19) = 3.20, p < 0.01].

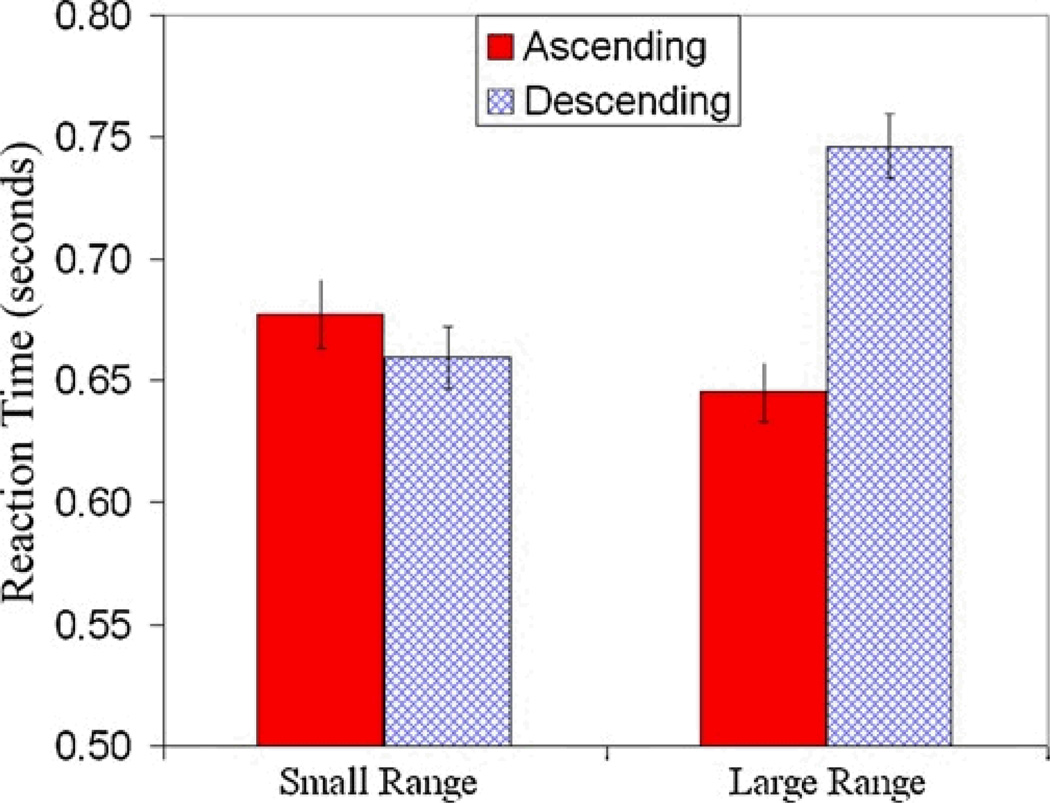
As can be seen in Figure 2, Mikulski’s semantic congruity effect for the small range showed a “funnel effect” whereby RT was significantly shorter for small values on ascending trials compared to descending trials and there was no difference between the two trial types for large values. In contrast for Schroeder on both ranges and for Mikulski on the large range, the semantic congruity effect was a true crossover effect (Holyoak, 1978). The finding that the semantic congruity effect held for both ranges indicates that the monkeys treated the largest values in the small range as small values when they were presented within the context of the larger range. To more closely examine this context effect we examined RT on the 6:12 pair which was a critical pair because it was the largest pair of values in the small range and the smallest pair of values in the large range. As shown in Figure 3, monkeys were on average 35 msec faster on ascending trials than descending trials when 6:12 was a relatively small pair (in the large range). In contrast, monkeys were, on average, 106 msec faster on descending trials than on ascending trials when 6:12 was a relatively large pair (in the small range).

Figure 3.

Figure 3

Open in a new tab

Mean RTs averaged across both monkeys on the pair 6 vs. 12 for all correct trials in the small and large ranges. When the pair 6 vs.12 was the largest set of values in the small range, monkeys were, on average, faster to choose the larger than to choose the smaller of the two arrays. In contrast, when the pair 6 vs. 12 was the smallest set of values in the large range, monkeys were, on average, faster to choose the smaller than to choose the larger of the same two arrays.

An ANOVA for Direction (ascending, descending) X Range [Small (1:2 through 6:12), Large (6:12 through 36:72)] on Schroeder’s RT to the pair 6:12 revealed a main effect of Range [F(3,39) = 11.76, p < 0.01], reflecting her overall faster responses on trials in the small range than trials in the large range, as well as a significant interaction between the Range and the Direction in which she was required to respond (ascending vs. descending) [F(3,39) = 17.67, p < 0.001]. This interaction indicates that, when the pair 6:12 was a relatively large pair in the small range, Schroeder was faster to choose the larger than to choose the smaller of the two arrays [t(9) = 3.20, p < 0.05], whereas when the same numerosity pair was presented in the large range and therefore was a relatively small pair, Schroeder was faster to choose the smaller than to choose the larger of the two arrays [t(9) = 3.76, p < 0.01].

The same analysis on Mikulski’s RT revealed a main effect of Direction [F(3,39) = 4.76, p < 0.05], reflecting her overall faster responses to the pair 6:12 on ascending trials than descending trials. She also showed a trend towards a significant interaction between the Range and the Direction of the comparison stimuli [F(3,39) = 2.34, p = 0.13].

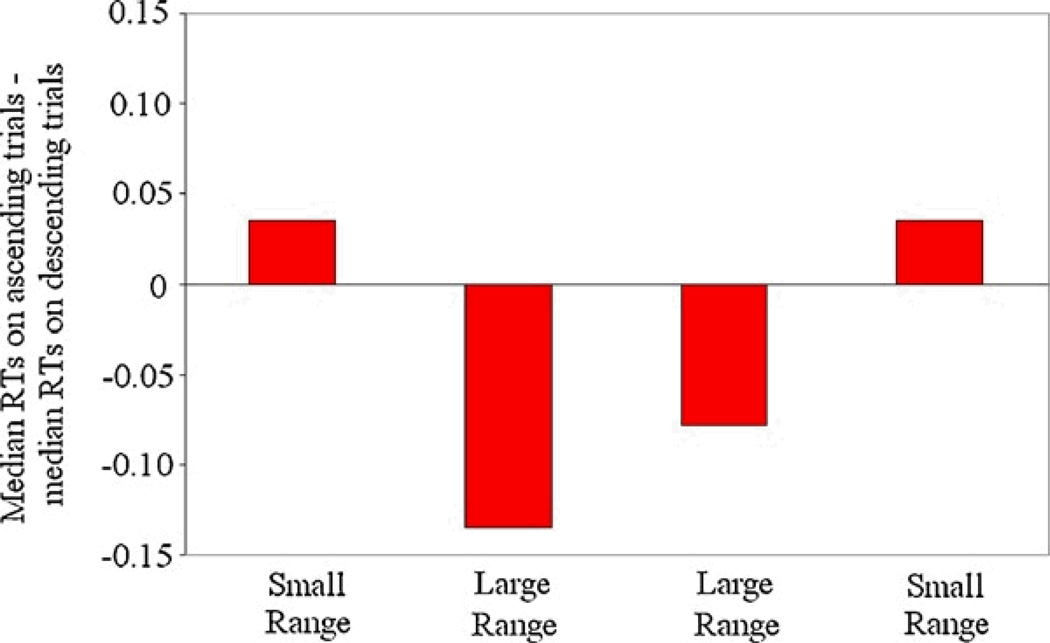
A final analysis assessed when the contextual shift took place by examining response times to the smallest pairs (6 vs. 12 and 12 vs. 24) in the large range. A contextual shift would result in monkeys being faster at ascending trials for the pair 6 vs. 12 in the large range, despite the fact that it was previously the largest pair in the small range (Figure 4). Given how few trials were available for the pair 6 vs. 12 from each session, we included the next smallest pair, 12 vs. 24, to increase power. A contextual shift would also result in monkeys being faster on ascending trials for 12 vs. 24, even though these values were larger than any pair in the small range. We conducted T-tests comparing the RTs for these pairs on ascending vs. descending trials on the sessions following the switch from the small to the large range. Despite the fact that both monkeys at the end of small-range testing, were faster at ordering the largest pair (6 vs. 12) when given a descending compared to ascending cue, both monkeys quickly became faster at ordering the 6 vs. 12 and 12 vs. 24 pairs in ascending order when these pairs were presented in the large range context. Schroeder was faster on ascending than descending trials on these pairs by the third session of large-range testing [t(47) = −2.020, p < 0.05] and Mikulski showed the same effect on the very first large-range session [t(44) = −2.202, p < 0.05].

Figure 4.

Figure 4

Open in a new tab

Median RTs for descending trials for the pair 6 vs. 12 subtracted from median RTs for ascending trials for the pair 6 vs.12. Data reflects the average of the median RTs for correct trials for the 5 sessions of each block averaged for the two monkeys. Positive values indicate that the monkeys were faster on descending trials compared to ascending trials for the pair 6 vs. 12, whereas negative values indicate the reverse. Monkeys showed a rapid contextual shift between blocks such that in blocks of small range sessions, monkeys were faster on descending trials, and in blocks of large range sessions, monkeys were faster on ascending trials for the 6 vs. 12 pair.

Discussion

Our findings provide further evidence against linguistic coding models of the semantic congruity effect. Both monkeys showed striking semantic congruity effects replicating a prior report by Cantlon & Brannon (2005). The novel aspect of our study however is that, the semantic congruity effect in monkeys is influenced by context as was previously reported in humans (Cech & Shoben, 1985). Specifically a given pair of values was treated as small or large depending on the range of values in which it was presented. Thus our data indicate that the cognitive process that monkeys use to compare the numerical value of two arrays of dots shares yet another important feature with the comparison processes of human adults, the context effect of numerical comparisons.

Another question that could be addressed by our results was how quickly the monkeys responded to a shift in context. Cech, et al (1990) and Petrusic & Baranski, (1989) found that adult humans respond to a shift in context very rapidly (e.g., within 40–92 trials). Cech, et al (1990) asked human adults to select either the larger or the smaller of a pair of animals. Small animals were paired only with other small animals and large animals were paired only with other large animals (the ranges did not overlap: all small animals were smaller than all large animals). The authors reported a context effect in RTs to the largest pair in the small range and the smallest pair in the large range that was established within the first 40–92 trials. The authors suggest that initial sampling of pairs may determine how subjects determine what is relatively large or small.

Petrusic & Baranski (1989) similarly reported that adults rapidly adjust they way they code stimuli based on context. Pairs of weighted objects were presented in blocks of 46 trials and participants were asked to choose either the lighter or the heavier object. Data from the first block of trials showed a funnel effect, while data from the second block of trials showed a full cross-over semantic congruity effect. The authors interpreted this to indicate that the reference point against which the stimuli were compared shifted rapidly (within the first 92 trials) to one more appropriate for the range of the stimuli. Our analyses indicate that like adult humans, monkeys rapidly shift their response strategies and show a contextual shift within the first few sessions in which the range of values is changed.

In summary, our findings provide further support for a numerical comparison process shared by monkeys and humans. The numerical semantic congruity effect is found in both species and is similarly sensitive to contextual anchoring. Monkeys respond to identical stimuli differently depending on the context in which those stimuli are presented. We suggest that an adequate model of the human comparison process should account for both the semantic congruity effect and the context effect without invoking linguistic coding.

Acknowledgements

We thank Monica Carlson, Melissa Libertus, David Paulsen, Nick DeWind and all of the members of the E.M.B. laboratory for their help in collecting data and discussing the results.

Footnotes

1

The first A block for Schroeder contained only 4 sessions due to an experimenter error. The data for Schroeder’s missing session (fifth session in the first block of the smaller range) was replaced by the average accuracy from the first four sessions within the small range.

2

Trials in which density was equated between the two arrays (30% of trials) and trials in which density was incongruent with number (20% of trials) were collapsed for analysis.

References

  1. Audley RJ, Wallis CP. Response instructions and the speed of relative judgements: I. Some experiments on brightness discrimination. British Journal of Psychology. 1964;55(1):59–73. doi: 10.1111/j.2044-8295.1964.tb02712.x. [DOI] [PubMed] [Google Scholar]
  2. Banks WP. Encoding and processing of symbolic information in comparative judgments. In: Bower GH, editor. The psychology of learning and motivation. Vol. 11. New York: Academic Press; 1977. pp. 101–159. [Google Scholar]
  3. Banks WP, Clark HH, Lucy P. The Locus of the Semantic Congruity Effect in Comparative Judgments. The entity from which ERIC acquires the content, including journal, organization, and conference names, or by means of online submission from the author. Journal of Experimental Psychology: Human Perception and Performance. 1975;104(1):35–47. [Google Scholar]
  4. Banks WP, Fujii M, Kayra-Stuart F. Semantic Congruity Effects in Comparative Judgments of Magnitudes of Digits. Journal of Experimental Psychology: Human Perception and Performance. 1976;2(3):435–447. [Google Scholar]
  5. Brannon EM. Quantitative thinking: From monkey to human and human infant to adult. In: Dehaene S, Duhamel J, Hauser MD, Rizzolatti G, editors. From Monkey Brain to Human Brain. Cambridge, MA: MIT Press; 2005. pp. 97–116. [Google Scholar]
  6. Brannon EM. The representation of numerical magnitude. Current Opinion in Neurobiology. 2006;16:222–229. doi: 10.1016/j.conb.2006.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Cantlon J, Brannon EM. Semantic congruity affects numerical judgments similarly in monkeys and humans. Proceedings of the National Academy of Sciences. 2005;102(45):16507–16511. doi: 10.1073/pnas.0506463102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Cech C, Shoben E. Context effects in symbolic magnitude comparisons. Journal of Experimental Psychology: Learning, Memory and Cognition. 1985;11(2):299–315. doi: 10.1037//0278-7393.11.2.299. [DOI] [PubMed] [Google Scholar]
  9. Cech C, Shoben E, Love M. Multiple congruity effects in judgments of magnitude. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1990;16(6):1142–1152. [Google Scholar]
  10. Dehaene S, Akhavein R. Attention, automaticity and levels of representation in number processing. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1995;21:314–326. doi: 10.1037//0278-7393.21.2.314. [DOI] [PubMed] [Google Scholar]
  11. Dehaene S, Izard V, Spelke E, Pica P. Log or linear? Distinct intuitions of the number scale in Western and Amazonian indigene cultures. Science. 2008;320:1217–1220. doi: 10.1126/science.1156540. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Feigenson L, Dehaene S, Spelke E. Core systems of number. Trends in Cognitive Sciences. 2004;8:307–314. doi: 10.1016/j.tics.2004.05.002. [DOI] [PubMed] [Google Scholar]
  13. Gallistel CR, Gelman R. Nonverbal numerical cognition: from reals to integers. Trends in Cognitive Sciences. 2000;4:59–65. doi: 10.1016/s1364-6613(99)01424-2. [DOI] [PubMed] [Google Scholar]
  14. Holyoak KJ, Mah W. Cognitive reference points in judgments of symbolic magnitude. Cognitive Psychology. 1982;14:328–352. [Google Scholar]
  15. Holyoak K. Comparative judgments with numerical reference points. Cognitive Psychology. 1978;10:203–243. [Google Scholar]
  16. Moyer RS, Bayer RH. Mental comparison and the symbolic distance effect. Cognitive Psychology. 1976;8:228–246. [Google Scholar]
  17. Nieder A, Miller EK. Analog numerical representations in rhesus monkeys: Evidence for parallel processing. Journal of Cognitive Neuroscience. 2004;16:889–901. doi: 10.1162/089892904970807. [DOI] [PubMed] [Google Scholar]
  18. Petrusic WM, Baranski JV. Semantic congruity effects in perceptual comparisons. Perception & Psychophysics. 1989;45:439–452. doi: 10.3758/bf03210718. [DOI] [PubMed] [Google Scholar]
  19. Petrusic WM, Baranski JV, Kennedy R. Similarity comparisons with remembered and perceived magnitudes: Memory psychophysics and fundamental measurement. Memory and Cognition. 1998;26:1041–1055. doi: 10.3758/bf03201182. [DOI] [PubMed] [Google Scholar]
  20. Pica P, Lemer C, Izard V, Dehaene S. Exact and approximate arithmetic in an Amazonian indigene group. Science. 2004;306:499–503. doi: 10.1126/science.1102085. [DOI] [PubMed] [Google Scholar]
  21. Whalen J, Gallistel CR, Gelman R. Non-verbal counting in humans: the psychophysics of number representation. Psychological Science. 1999;10:130–137. [Google Scholar]

RESOURCES