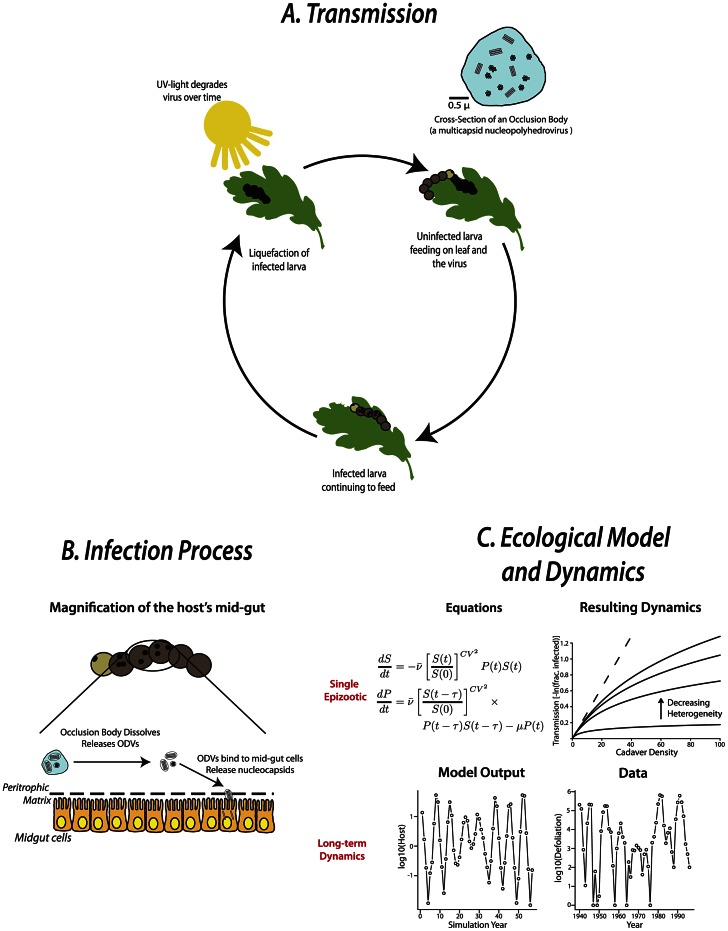
Figure 1. Typical baculovirus transmission cycle, the infection process, and resulting ecological dynamics in lepidopteran larvae.

A) The transmission cycle begins when an uninfected larva consumes occlusion bodies (OBs) containing either multiple or single copies of the baculovirus. If enough OBs are consumed, the virus establishes in the midgut of the host and eventually spreads throughout the body of the now infected larva. Eventually, liquefaction of the host occurs as the host's body tissue is consumed by the virus, resulting in millions of OBs within a single larva. The virus triggers the larval integument to split open, releasing the newly formed OBs into the environment to continue the cycle. Over time, the OBs degrade due to ultraviolet light exposure. B) Within the larvae, the OB's protein coat dissolves, releasing the occlusion-derived viruses (ODVs). The ODVs bind to the midgut cells and, in turn, release their nucleocapsids into the cells' cytoplasm. The nucleocapsid uncoats and begins reproduction once it is transported to the nucleus. C) During a single epizootic, the change over time (t) in the density of susceptible individuals (S) and pathogen-infected cadavers (P) in the environment depends upon the mean transmission rate (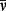) between the two, the coefficient of variation (CV) associated with that rate, the time between infection and death (τ), and the degradation of the virus in the environment (μ). For a given transmission rate 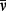, a population's heterogeneity has a dramatic impact on disease transmission. As individuals become more similar, heterogeneity between them decreases and overall transmission increases. When all individuals share the same transmission rate, transmission becomes linear (the dotted line in the “Resulting Dynamics” figure) as pathogen-infected cadaver density increases. A long-term dynamic model for the gypsy moth derived from the equations shown [7] does a reasonably good job of replicating the pattern of forest acres defoliated in Maine from 1940 to 1996.