Embedding inertial-magnetic sensors in everyday objects: Assessing spatial cognition in children

Abstract

This paper describes an interdisciplinary approach to the assessment of children development of spatial cognition, with a focus on the technology. An instrumented toy (block-box) is presented which embeds magneto-inertial sensors for orientation tracking, specifically developed to assess the ability to insert objects into holes. The functional specifications are derived from experimental protocols devised by neuroscientists to assess spatial cognition skills in children. Technological choices are emphasized with respect to ecological requirements. Ad-hoc calibration procedures are presented which are suitable to unstructured environments.

Preliminary results based on experimental trials carried out at a day-care on typically developing children (12–36 months old) show how the instrumented objects can be used effectively in a semi-automatic fashion (i.e., rater-independent) to derive accurate measurements such as orientation errors and insertion time which are relevant to the object insertion task.

This study indicates that a technological approach to ecological assessment of spatial cognition in children is indeed feasible and maybe useful for identification and early assessment of developmental delay.

1. Introduction

How does our conception of three-dimensionality of space emerge? Through careful observation of children of all ages, a few decades ago Jean Piaget laid the foundations to understanding the development of spatial cognition in humans. Recent years have seen an effort towards more quantitative forms of assessment, as opposed to qualitative, observational and subjective methods used in classic studies since the early works of Piaget (1953). In this sense, motion analysis is becoming a fundamental tool for research as well as clinical practice.

Despite the broad spectrum of available “ammunitions” for motion analysis (Welch & Foxlin, 2002), ecological assessment imposes strict technological constraints. For example, the need for minimally structured environments makes the use of video-based technologies difficult, also due to the line-of-sight issues (e.g., during manipulation tasks performed by children, markers might not always be visible). Furthermore, motion tracking devices should be minimally obtrusive to the natural movements of the children and this makes, for example, the use of mechanical-sensing devices rather impractical. From a technological perspective, a very appealing possibility is represented by sourceless devices such as inertial and geo-magnetic sensors (Welch & Foxlin, 2002), already proved suitable for clinical gait analysis (Kemp et al., 1998). Being sourceless, such devices produce no electromagnetic radiation and, in this sense, raise no concern for the safety of children.

Restrictions to the use of this technology are due to the influence of external magnetic fields or distortion of the geo-magnetic field itself. In this sense, care must be taken to avoid large ferromagnetic objects (e.g., metal tables or chairs) or electromagnetic objects (electrical transformers, cellphones) in the immediate vicinity of the devices. While the naturalistic environments for children (e.g., kindergartens and daycares) typically use fully compatible materials such as plastic, rubber and wood, transportation of the devices from the laboratory to the experimental centre might cause de-calibration and loss of sensitivity for the sensors. For these devices to be useful in research, proper sensor calibration should be guaranteed in the first place, and various methods have been proposed which address the in-use (Lotters et al., 1998) and the in-field calibration (Campolo et al., 2006). Based on our previous experience with such devices (Taffoni et al., 2009; Campolo et al., 2011a,b), we summarize issues related to the effective use of Inertial- Magnetic Units (IMU), i.e., design and fabrication of wireless IMU-based devices for assessing spatial cognition in children, in-field calibration procedures, and finally data analysis. In particular, in this paper, we shall expand on our previous work and fully describe the algorithm behind attitude estimation and infield calibration. We shall also briefly present the laboratory tests used to assess the overall accuracy, for which full details are reported in Campolo et al. (2011a), as well as preliminary results of the final use of our device on regularly developing children.

2. Instrumented toys

Virtually any toy, tool or piece of garment used by children could be a good candidate to host all sorts of technology and “see what comes out” when the child wears it or plays with it.

Our approach is based on a closed-loop dialogue between neuroscientists and bioengineers: iteratively, starting from established protocols, we select appropriate technologies for a given scenario and at the same time redesign the protocols to include the proposed technology.

In the following, a platform specifically devised to investigate the development of spatial cognition in children is presented for which functional specifications are derived from protocols of experiments of interest for neuroscientists.

The aim is twofold: on one hand, we wish to provide scientists with novel technological platforms for the unobtrusive and ecological assessment of behavioral development in children; on the other hand, these platforms should enable/facilitate the transition from research to clinical practice.

2.1. Assessing spatial cognition skills

By the end of the first year of life, children start to pile-up blocks, put lids on cans and insert objects into apertures. Through these activities, the child learns to plan actions that involve more than one item. The ability to solve such problems reflects the childs spatial, perceptual and motor development. In particular, the ability to represent objects in different positions and orientations must be in place before they can be fit into apertures.

Recent studies by Ornkloo & von Hofsten (2007) show developmental curves, based on statistical rates of success of object-fitting tasks, relative to children aged 14—26 months.

Specifically, the tasks consisted of inserting cylindrical objects, hereafter “blocks”, with different cross-sections into a box with similar holes on its lid. The experimental scenario and the shapes of blocks inspired by Ornkloo & von Hofsten (2007) are shown in Fig. 1. All the blocks had similar dimensions, 1 mm smaller than the apertures. Different cross-sections were used, which would require similar hand aperture in grasping. The only difference was the number of possibilities they could fit into the corresponding aperture (i.e., infinite possibilities for the circular cross-section, four possibilities for the squared cross-section and three possibilities for the triangular cross-section).

Fig. 1.

Block-box experimental scenario.

Ornkloo & von Hofsten (2007) assessed (among other things) the horizontal and vertical pre-adjustments. The outcome was yes/no (i.e., successful or unsuccessful) based on the alignment errors between the block and the box. Both the vertical error (angular misalignment between the longitudinal axis of the block and verticality) and the horizontal error (angular misalignment between the orientations of the cross-section and the aperture) were estimated from the videos acquired with two cameras. A trial was considered unsuccessful for misalignments exceeding 30 degree. Accuracy of such methods highly depends on the quality of the videos. As highlighted by Ornkloo & von Hofsten (2007), the vertical and horizontal alignments were judged by two coders who disagreed on 31 out of 302 cases, i.e., on more than 10% of the times. Moreover, this method relies on the (time-consuming) manual scoring of videos, frame-by-frame.

2.2. Block-box platform

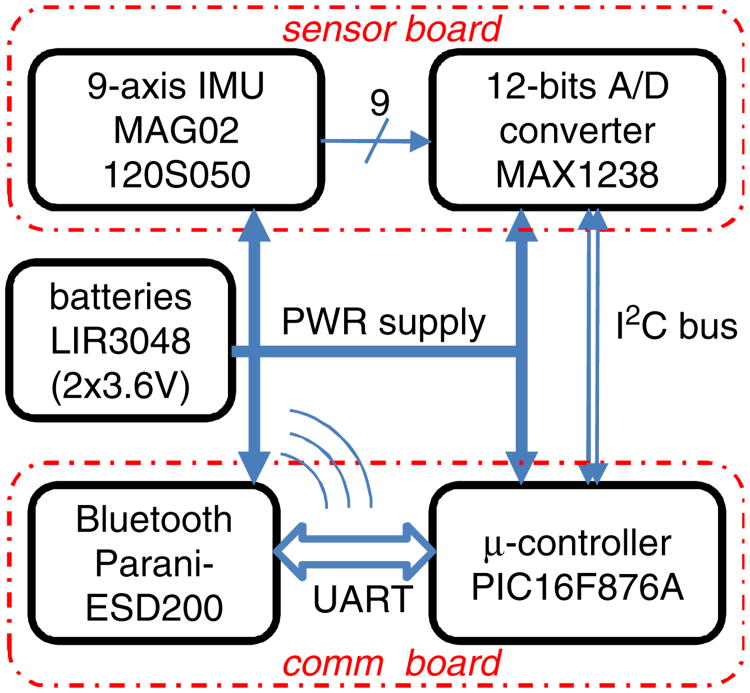
Inspired by such experiments and based on our previous experience with sensorized toys (Campolo et al., 2007), we developed a sensorized core (the overall architecture is shown in Fig. 2, CAD drawings and physical implementation are shown in Fig. 3) to be embedded in blocks with various cross-sections, shown in Fig. 4.

Fig. 2.

Architecture of the sensorized core.

Fig. 3.

CAD drawing and photograph of the sensorized core, consisting of a kinematics sensing unit and communication board.

Fig. 4.

Photograph of the prototyped sensorized core and outer shells.

In particular, we found that from an ecological perspective, the sourceless orientation estimation via inertial and magnetic sensors is especially suited to this application. Accelerometers can in fact be used to measure tilt while magnetometers can be used as a compass to measure horizontal misalignments. Gyroscopes are required to compensate for non-static effects.

Figures 2 and 3 show the sensing core, mainly consisting of a compact (17.8 mm × 17.8 mm × 10:2 mm), micro-fabricated 9-axis inertial-magnetic sensor (model MAG02-1200S050 from Memsense Inc.). In particular, the device is designed to sense ± 2 g accelerations, ± 1200 deg/s angular rates, ± 1 Gauss magnetic fields, all within a 50-Hz bandwidth. The sensors are coupled with a multi-channel, 12-bit AD converter (model MAX1238 from Maxim Inc.) which can retransmit sampled data over a 4-wires I2C bus. For our application, we sample each of the nine channels at 100 samples/s. Such data are collected and rearranged in a specific message format by a microcontroller and then retransmitted via a bluetooth device. Finally, two 3.6-V Li-Ion Rechargeable batteries (LIR3048 from Powerstream Inc.) are used in series which guarantee approximately an hour of autonomous operation. Data transmitted over the bluetooth interface are collected by a nearby PC, for off-line data analysis.

2.3. In-field calibration protocol

Magnetometers are meant to sense the geomagnetic field and provide its components [b_x, b_y, b_z]^T along the x̂, ŷ and ẑ axes of the sensing device itself (such axes move with the moving frame). Similarly, the accelerometers are meant, in static conditions, to read out the components of the gravitational field [g_x, g_y, g_z]^T along the same axes.

Calibration of such sensors is straightforward when one can reliably count on precision alignment procedures, e.g., in a laboratory setting. In (Campolo et al., 2006), a procedure for in-field calibration of magnetometric sensors was presented which does not rely on previous knowledge of magnitude and direction of the geomagnetic field and which does not require accurately predefined orientation sequences. Such a method can be applied to accelerometers as well and is especially suited for clinical applications. The procedure relies on the fact the geomagnetic (or gravitational) field has constant components in the fixed frame. As the orientation of the sensors vary, the components in the moving frame also vary but the magnitude of the field keeps constant, i.e., the components are bound to lie on a sphere. Readouts from non-calibrated sensors are therefore bound to lie on an ellipsoid, see (Campolo et al., 2006) for details. Via the least-square method it is possible to robustly estimate the centroid and semi-axes length of the ellipsoid which coincide with the calibration parameters (gain and offsets for each axis).

Based on this method, a calibration protocol was devised to provide a sufficient number of measurements for the algorithm to robustly converge. The instrumented toy (of whatever shape) is secured inside a wooden box, shaped as a parallelepiped, so that the toy does not move as the box is displaced around.

Magnetometers

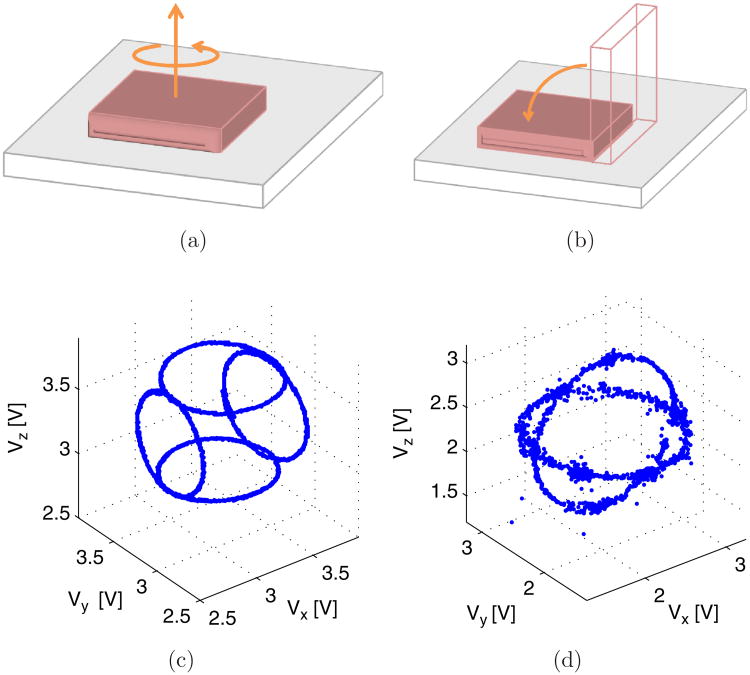
As in Fig. 5(a), the box is placed on a table and an approximately 360 degree rotation (no need to be accurate) is performed by keeping one face of the box always parallel and in contact with the table. The same procedure is repeated for four different faces.

Fig. 5.

Calibration sequences for (a) magnetometers and (b) accelerometers. Plots of the measurements (i.e., voltages V_x, V_y and V_z from the triaxial sensors) derived from the calibration sequences for (c) the magnetometers and (d) the accelerometers.

Accelerometers

As in Fig. 5(b), the box is placed on a table and smoothly (i.e., avoiding shocks) tilted by 90 degrees along one edge, this is repeated four times¹ until the box returns in the initial position. The whole procedure is repeated with a different initial position.

Gyroscopes

The procedure is similar to the one deployed for the accelerometers.

Measurements derived from a calibration sequence are shown in Figs. 5(c) and 5(d), respectively for the magnetometers and for the accelerometers. The least-squares algorithm is then used to derive the best fitting ellipsoids (one for the magnetometers and one for the accelerometers) whose surfaces contain the two sets of measurements.

As previously mentioned, since the geomagnetic field is constant, its components in the moving frame are bound to lie on the calibrating ellipsoid, not only during the calibration sequences but for every possible movement. For this reason, movements performed during the regular use of the toy, i.e., when the children play with it, can be used for updating the calibration parameters, or at least for an on-line check. Similar procedures apply to accelerometers, paying attention to consider only the quasi-static movements, i.e., when accelerations of the movement itself are negligible with respect to gravity. Details about “in-use” calibration can be found in (Lotters et al., 1998).

2.4. Attitude estimation from calibrated sensors

Complementary and Kalman filters have traditionally been used to design attitude observers, especially in presence of redundant measurements. Kalman filters work in the time domain focusing on the noise corrupting the signals and leads to optimality when the noise is Gaussian (Brown & Hwang, 1992). Complementary filters approach the problem from the frequency domain, falling in the category of the so called Wiener filters, i.e., less general when it comes to dealing with noise. It should be noted however that in real applications such as navigation assuming white, Gaussian noise is definitely a strong assumption.

The natural configuration space for a rigid body is the so-called Special Orthogonal group SO(3), i.e., the space of 3 × 3 rotation matrices R such that R⁻¹ = R^T and det R = +1. As shown in Arnold (1989), SO(3) is a three-dimensional space and, for every smooth curve on SO(3), the quantity

$$\widehat{\omega }=R^TṘ$$ (2.1)

is a skew-symmetric matrix, where ·̂ is the hat operator (A1) and ω is the body angular velocity (Ṙ is the time derivative of the orientation matrix R).

The body angular velocity is a three-dimensional vector which can be directly measured by a set of triaxial gyroscopes fixed on the rigid body. Ideally, we can get the orientation just by integrating Eq. (2.1) but noise, bias and sensitivity errors from the gyroscopes would rapidly lead to large drift errors.

In static conditions (ω = 0), calibrated data from accelerometers and magnetometers are sufficient to determine the orientation R with respect to a global fixed frame defined by gravity and by the geomagnetic North (Campolo et al., 2006). In dynamic conditions, especially at higher frequencies, this estimate is much less reliable and is traditionally fused with information from the gyroscopes for robust attitude tracking by means of complementary and Kalman filters. Although Kalman filters can be extended (EKF) to nonlinear cases, they fail to fully capture the nonlinear and noncommutative of 3D rotations, with risks of instabilities. On the other hand, nonlinear filters (Won et al., 2010; Daum, 2005), in particular complementary filters, are better suited to deal with 3D rotations. We developed a complementary filter for attitude estimations, as fully detailed in (Campolo et al., 2008, 2009a,b), and in particular its numerical implementation:

$$\begin{array}{c}{\omega }_n^{\ast }={\omega }_n+k_g(g_n\times (R_n^{\ast T}{g}_0\left)\right)+k_b(b_n\times (R_n^{\ast T}{b}_0\left)\right)\\ {\alpha }_n=sin\Vert \Delta T{\widehat{\omega }}_n^{\ast }\Vert /\Vert \Delta T{\widehat{\omega }}_n^{\ast }\Vert \\ {\beta }_n=1-cos\Vert \Delta T{\omega }_n^{\ast }\Vert /{\Vert \Delta T{\widehat{\omega }}_n^{\ast }\Vert }^2\\ R_{n+1}^{\ast }=R_n^{\ast }\left(I+{\alpha }_n\Delta T{\widehat{\omega }}_n^{\ast }+{\beta }_n\Delta T{\widehat{\omega }}_n^{\ast 2}\right)\end{array}$$ (2.2)

where ‖ · ‖ is the standard Euclidean norm; k_g and k_b are scalar gains²; ΔT is the sampling time (10 ms); g₀ and b₀ are the readings at initial time t₀ from, respectively, accelerometers and magnetometers; g_n, b_n, and ω_n are the readings at discrete time t_n = t₀ + nΔT from accelerometers, magnetometers and gyroscopes, respectively; $R_n^{\ast }$ is the orientation matrix estimate at time t_n. By construction, the numerical filter Eq. (2.2) guarantees that $R_n^{\ast }\in SO\left(3\right)$ at all times (Campolo et al., 2009b). The overall accuracy for our sensorized core is less 2 degrees angular root-mean-square error, for details see (Campolo et al., 2011a).

When a cylinder is presented to the child, it is always aligned with the hole and the initial frame of reference could be defined so that e₃ := [0 0 1]^T is the vertical axis aligned with gravity while e₁ := [1 0 0]^T and e₂ := [0 1 0]^T are the horizontal axes heading North and West, respectively. In this way, at all time, the vertical (| ∊_υ|) and horizontal (| ∊_h|) angular misalignments can be determined directly from the projections of two moving axes (R_ie₃ and R_ie₁) onto the fixed axes (e₁, e₂, e₃), i.e.,

$${\in }_{\upsilon }:=\text{a}cos\left(e_3^T{R}_i{e}_3\right)[\text{wrap}\pm \frac{\pi }{2}]$$ (2.3)

$${\in }_h:=\text{a}tan2(-e_2^T{R}_i{e}_1,e_1^T{R}_i{e}_1)[\text{wrap}\pm \frac{\pi }{N}]$$ (2.4)

where the [wrap ± π/N] operation ensures that ∊_h is wrapped within ± π/N, where N is the number of possible insertions³ of the block.

3. Preliminary experiments with the block-box

The block-box prototypes described in previous sections were tested with several typically-developing children, aged 12–36 months, at a day-care in Rome.

3.1. Experimental protocol

We used three sensorized blocks, respectively with circular (CIR), squared (SQR) and hexagonal (HEX) cross-sections. The blocks were presented to the child one at a time, either vertically or horizontally, and each block was always associated with a lid with a corresponding aperture, as in Fig. 6. The order of presentation was pseudo-random. Snapshots from a video of a representative trial are shown in Fig. 7.

Fig. 6.

Different cross-sections for the cylindrical blocks and corresponding apertures.

Fig. 7.

Snapshots of an experimental trial. The video is also provided as supplemental multimedia material.

Each task consisted of grasping (Fig. 7(a)) the presented block, transporting it over the aperture (Fig. 7(b)), inserting with possible adjustments (Fig. 7(c)) and releasing it into the aperture (Fig. 7(d)). For each presented block the task was repeated three times. Children were completely free to perform the task at their own pace. Often the children were distracted by the environment (e.g., other children in the daycare) and so most of the children interrupted the task. In this paper, we present data relative to three children who completed the insertion tasks without interruptions.

3.2. Data analysis

The raw data collected from the inertial-magnetic sensors embedded in each presented block were processed off-line. Data were first fed into a complementary filter (Campolo et al., 2008, 2009a,b) to derive the sequence of orientations of the block (100 per s).

Once the orientation of the block was determined, the vertical and horizontal errors can be derived at any time as, respectively, the angular tilt with respect to gravity and the angular misalignment in the horizontal plane between the current orientation and the orientation of the block, once inserted. Pre-adjustment errors are defined as the vertical and horizontal errors at the time of first contact, i.e., when the first impact between the sensorized block and the lid of the box occurs, which as in Ornkloo & von Hofsten (2007) was determined from inspecting the video.

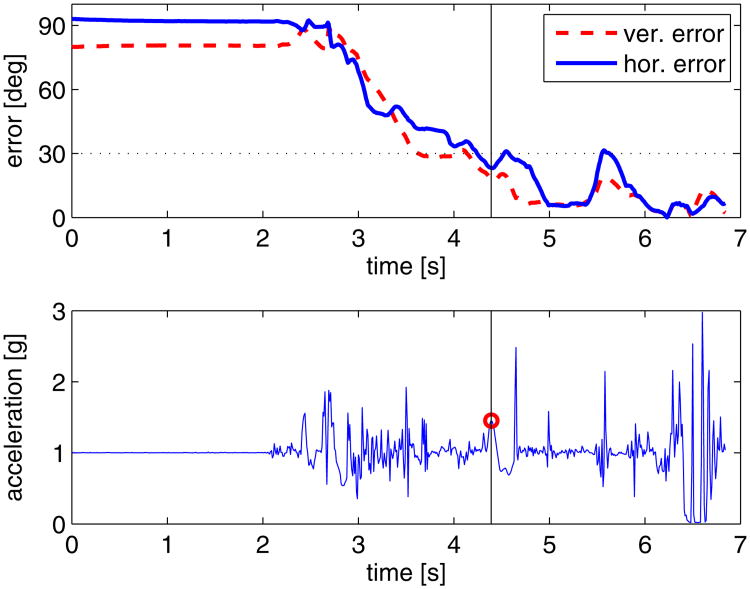
Figure 8 reports data from a representative trial. The block is presented to the child, who grasps it approximately at time t = 2.1 s (when the first vibrations appear in the accelerometer plots, bottom figure). The time of first contact occurs approximately at t = 4.4 s and it corresponds to a peak in the acceleration trace (marked with a circle). At this time, both vertical and horizontal errors are below 30 degrees, so the pre-adjustment would be considered correct according to Ornkloo & von Hofsten (2007). In the remaining time, the child tries to fit the the block into the aperture and only at approximately time t = 6.4 s both vertical and horizontal alignment errors drop to zero and the block can be successfully inserted.⁴ The time interval between the first contact and a successful insertion is called insertion time, see Fig. 8 (bottom).

Fig. 8.

Representative data acquired during experiments with the block-box. (Top) Horizontal and vertical angular errors between the sensorized block and corresponding aperture. (Bottom) Acceleration amplitude: the circle at approximately t = 4.4 s denotes the time of first contact between the block and the lid of the box.

3.3. Preliminary results

Preliminary tests have been carried out on four children, three 25 months old female and one 14 months old male (i.e., the age range of interest for the development of orientation skills). Their data were grouped together for statistical analysis. Table 1 reports data relative to horizontal and vertical errors, i.e., angular misalignments from Eqs. (2.3)–(2.4), as well as to the insertion time. For each measured variable, mean and standard error (SE) are reported. The first three rows are relative to vertically presented blocks, the second three rows are relative to horizontally presented blocks. Note that the horizontal error is by definition zero for the block with circular cross-section (CIR) as all horizontal orientations are in fact possible for the block to fit the corresponding aperture.

Table 1.

Mean values (± standard error) of the horizontal error (| ∊_h|), vertical error (| ∊_υ|) and the insertion time (Time) averaged on three subjects for three sensorized blocks with different cross-sections (CIR, SQR, and HEX) and for two different presentations (horizontal and vertical).

	| ∊h| Mean ± SE [deg]	| ∊υ| Mean ± SE [deg]	Time Mean ± SE [sec]
Horizontal presentation
CIR	—	23.4 ± 4.9	2.0 ± 0.8
HEX	18.2 ± 3.3	22.3 ± 4.6	4.7 ± 1.5
SQR	11.52 ± 3.54	16.9 ± 3.9	1.9 ± 0.6
Vertical presentation
CIR	—	14.9 ± 4.8	1.6 ± 0.4
HEX	14.6 ± 2.0	18.3 ± 3.2	3.8 ± 1.0
SQR	22.0 ± 4.04	11.81 ± 2.73	3.4 ± 0.9

Despite the small number of subjects and completed tasks, there are some considerations which can inferred from the data reported in the table. The insertion time seems to depend on the initial presentation of the block. For all blocks, the insertion time for the horizontal presentation was consistently larger than that measured for the vertical presentation. This is probably related to pre-adjustment errors which tend to be consistently larger for horizontally presented blocks (except for the horizontal error of the squared section block): a larger per-adjustment error may require more time to perform the corrections necessary to insert the block into the hole. Moreover, such data are consistent with the fact that horizontally presented blocks require greater computational efforts for motor planning (e.g., performing mental rotations) as well as in online control since the child has to correct both horizontal and vertical errors at the same time.

Note: Given the limited number of completed trials, our analysis lacks statistical power and we might not be able to detect some effects, e.g., due to shape. The presented experiments mainly aim at proving feasibility of the method and acceptability of the device by the children.

4. Conclusion

Developmental milestones of children have long been object of study (e.g., see the works of Piaget (1953)), nevertheless quantitative normative databases of sensorimotor integration skills in relation to increasingly complex tasks are still lacking. Such information extend the current knowledge on developmental mechanisms, with an impact on Developmental Sciences as well as on bio-inspired Robotics.

We propose a mechatronic platform for assessing the development of spatial cognition in children based on experimental scenarios devised by psychologists. The selection of the technology strictly follows the ecological requirements.

In particular, we present an instrumented toy specifically devised to assess the development of spatial cognition in children. The scientific focus is on the children's ability to mentally rotate a block in order to fit the appropriate hole.

The experimental protocol is adapted from that originally proposed by Ornkloo & von Hofsten (2007), specifically devised to assess vertical and horizontal pre-adjustments of the block (with various levels of difficulty in relation to the different cross-sections) at the time of contact with the box. In the work of Ornkloo & von Hofsten (2007), two video cameras monitored the experiment providing respectively a top and a side view. From the videos, after determining the frame during which the block came first into contact with the lid of the box, both vertical and horizontal alignment of the block with the aperture were evaluated from the specific frame, with a goniometer.

Accuracy of such methods highly depends on the quality of the videos. As highlighted by Ornkloo & von Hofsten (2007), the vertical and horizontal alignments were judged by two coders who disagreed on 31 out of 302 cases, i.e., on more than 10% of the times. Moreover, this method relies on the (time-consuming) manual scoring of videos, frame-by-frame.

The block-box platform embeds magnetic-inertial sensors for attitude estimation. Both vertical and horizontal alignments can be derived automatically from the orientation estimated from the raw data, with 1–2-degree accuracy (as shown in Table 1). Furthermore, the proposed platform allows for analysis of orientation at all times, not only at the insertion time. The platform was also successfully tested with healthy children, to assess acceptability and robustness as well as to derive a first set of normative data. Results from this pilot study will be part of future publications. In conclusion, the proposed block-box platform proved suitable for use in day-cares, with the potential of becoming a screening tool for a large number of children.

Appendix

The hat operator maps a vector a = [a₁ a₂ a₃]^T into a skew-symmetric matrix:

$$\widehat{\cdot }:\mathit{\text{a}}=\left[\begin{array}{c}{a}_1\\ a_2\\ a_3\end{array}\right]\to \left[\begin{array}{ccc}0& -a_3& a_2\\ a_3& 0& -a_1\\ -a_2& a_1& 0\end{array}\right]=\widehat{\mathit{\text{a}}}$$ (A1)

The Logarithmic map (Park & Martin, 1994; Park, 1995) on SO(3) maps a rotation matrix into a skew-symmetric one:

$$\widehat{r}=\text{log}R:=\frac{\theta }{2\text{sin}\theta }\left(R-R^T\right)$$ (A2)

where θ satisfies 1 + 2 cos θ = trace(R). The physical significance of this map is that any rotation R can be thought of as a pure rotation about a fixed axis r through an angle ‖r‖ = θ.