Using Frankenstein’s Creature Paradigm to Build a Patient Specific Atlas

Abstract

Conformal radiotherapy planning needs accurate delineations of the critical structures. Atlas-based segmentation has been shown to be very efficient to delineate brain structures. It would therefore be very interesting to develop an atlas for the head and neck region where 7 % of the cancers arise. However, the construction of an atlas in this region is very difficult due to the high variability of the anatomies. This can generate segmentation errors and over-segmented structures in the atlas. To overcome this drawback, we present an alternative method to build a template locally adapted to the patient’s anatomy. This is done first by selecting in a database the images that are the most similar to the patient on predefined regions of interest, using on a distance between transformations. The first major contribution is that we do not compute every patient-to-image registration to find the most similar image, but only the registration of the patient towards an average image. This method is therefore computationally very efficient. The second major contribution is a novel method to use the selected images and the predefined regions to build a Frankenstein’s creature” for segmentation. We present a qualitative and quantitative comparison between the proposed method and a classical atlas-based segmentation method. This evaluation is performed on a subset of 58 patients among a database of 105 head and neck CT images and shows a great improvement of the specificity of the results.

1 Introduction

Conformal radiotherapy allows to precisely target the tumor while keeping an acceptable level of irradiation on neighboring critical structures. This however requires to accurately locate the tumor and the organs at risk in order to determine the best characteristics of the irradiation beams. This delineation task is usually done manually and is therefore very long and not reproducible.

To solve this problem, atlas-based segmentation has been shown to produce accurate and automatic segmentations of the brain [1], allowing to take into account easily the relative positions of the structures. The construction of an atlas for other regions such as the head and neck region, where 7 % of the cancers arise, is therefore of great interest [2, 3]. Methods have been presented for the construction of an unbiased average model from an image dataset such as [4, 5]. We presented in [6] a method to build a symmetric atlas from a database of images manually delineated following the guidelines in [7]. However, anatomical variability is very high in the head and neck region. An average atlas may therefore be very different from the patient, leading to registration discrepancies. Moreover, this variability may cause the mean contours to be too large in the atlas yielding over-segmentations.

To overcome these drawbacks, methods have been presented towards the creation of atlases whose anatomy is adapted to the patient [8, 9]. First, Blezek et al. [8] presented an interesting approach to cluster a database into several atlases representing homogeneous sub-populations. However, the selection of the most adequate atlas with respect to a given patient is not addressed. Another method [9] has been introduced to select the most similar images to the patient by comparing a similarity measure between each database image and the patient. This method is however computationally expensive, requiring to register all the database images on the patient. Moreover, a local comparison of the images is more adapted in our case, as our database consists of manually delineated patients who present pathologies that may corrupt a global comparison.

In this paper, we present the development of an atlas locally adapted to the patient to get more precise delineations than with an average atlas. To this end, we first present a new and efficient method to select the most similar images to the patient on predefined regions. Each most similar sample is defined as the one that needs the smallest local deformations to be registered on the patient. These images are then combined into a template image, as an analogy to Frankenstein’s creature [10], and used for segmentation.

We first present our approach to select the image that is the most similar to the patient P to delineate on a given region. We then focus on the combination of the local templates selected into one single template for delineation. Finally, we show qualitative and quantitative results on a database of 105 head and neck CT images, showing a great improvement of the specificity of the results.

2 Method

In this section, we present an efficient method to compute a template that is similar to the patient P on predefined regions R_l, based on the following steps:

• –Construction of an average atlas M from the database images (pre-computed)
• –Non linear registration of the patient P to delineate on M
• –Selection of the most similar image Ĩ_l for each local region R_l
• –Computation of the anatomy M̃ and segmentations from the set of Ĩ_l

2.1 Selection of the Locally Most Similar Images to a Patient

For each region of interest R_l, we select the most similar image among our database to the patient to delineate. It is defined as the one that is the “less” deformed to be non linearly registered on the patient. We denote by T_B←A the transformation linking two images A and B, so that B can be resampled on A (i.e. A ≈ B○T_{B ←A}). The selection for a given region R_l is then based on a comparison of the non linear transformations T_Ij←P to bring each image I_j of the database on P, i.e. the most similar image is defined as: Ĩ_l = arg min_Ij d_Rl (I_j, P) = arg min_Ij d_Rl (T_Ij←P, Id), where d_Rl will be defined later on. However, this type of comparison is computationally very expensive as it requires to perform all the registrations between P and the images I_j for each patient to segment. To perform an efficient selection, we therefore use an intermediate image: an average atlas M pre-computed from the database using [6].

From the average atlas construction, we obtain for each image I_j an affine transformation A_Ij←M and a non linear transformation T_Ij←M bringing it on the average image M. Moreover, when registering P on M, another non linear transformation T_P←M is computed. The key hypothesis is then to assume that T_Ij←P can be approximated by T_Ij←M ○ $T_{P\leftarrow M}^{-1}$. This hypothesis presents many advantages. First, the regions of interest R_l can be defined once and for all on the atlas image M. Moreover, this can be done very easily thanks to the average segmentations available on the atlas. Also, the similarity between P and I_j, d_Rl (T_Ij←P, Id), can be approximated using the following equation:

$$d_{R_l}(T_{I_j\leftarrow M}○T_{P\leftarrow M}^{-1},Id)=\sum _{i\in R_l○T_{P\leftarrow M}^{-1}}||\text{log}(T_{I_j\leftarrow M}○T_{P\leftarrow M}^{-1})(i)||$$ (1)

where i corresponds to the voxels of the dense transformation and d_Rl is the Log-Euclidean distance on diffeomorphisms [11] between the identity transformation and T_Ij←M ○ $T_{P\leftarrow M}^{-1}$. Using our hypothesis, we need to perform only one non linear registration between M and P to select the locally most similar images Ĩ_l for all regions R_l, therefore reducing drastically the computation time.

2.2 Piecewise Most Similar Atlas Construction

We now focus on the computation of a template for segmentation from the selected images Ĩ_l and the regions R_l. This template, similar to the Frankenstein’s creature [10], is built by iterating over the following steps to combine the images:

• –Registration of the images Ĩ_l on the average image at iteration k : M̃_k
• –Compute the new average image M_k+1, based on the regions R_l,k
• –Compute an average transformation T̄_k from the transformations T_Ĩl←M̃k
• –Apply ${\overline{T}}_k^{-1}$ to M_k+1 to get the new reference M̃_k+1 = M_k+1 ○ ${\overline{T}}_k^{-1}$
• –Update the regions of interest by applying ${\overline{T}}_k^{-1}$ to R_l,k : R_l,k+1 = R_l,k ○ ${\overline{T}}_k^{-1}$

This algorithm can be seen as an extension of [4] to the construction of an atlas where images have spatially varying weights, depending on the regions R_l. In contrast, Guimond et al. consider implicitly that all images have equal and spatially constant weights (1/N for each image if N images are averaged). The final step is then to associate a set of segmentations to this anatomy. This is done by transforming the manual segmentations of the image Ĩ_l present in the region R_l onto M̃, using the transformations obtained in the construction process, and ensuring that no overlap exists between the final structures.

Average Image Computation

To compute M_k+1 from the images Ĩ_l registered on M̃_k, we first need to define the spatial extensions of each region at iteration k : R_l,k. This will allow to use, on each R_l,k, only the corresponding Ĩ_l and to interpolate between the regions. The weight functions w̄_l,k(x) are computed in three steps: locally erode the regions R_l,k using the method presented in [12] to ensure a minimal distance between them, compute the inverse of the minimal distance to each R_l,k: w_l,k(x) = 1/(1 + αdist(x, R_l,k)), and normalize the $w_{l,k}(x):{\overline{w}}_{l,k}(x)=w_{l,k}(x)/{\sum }_{l=1}^L{w}_{l,k}(x)$.

The images Ĩ_l are then aligned onto M̃_k, first globally resulting in affine transformations A_Ĩl←M̃k, and then non linearly producing dense transformations T_Ĩl←M̃k. These transformations and the w̄_l,k(x) are then used to compute M_k+1:

$$M_{k+1}(x)=\sum _{l=1}^L{\overline{w}}_{l,k}(x)({\tilde{I}}_l○A_{{\tilde{I}}_l\leftarrow {\tilde{M}}_k}○T_{{\tilde{I}}_l\leftarrow {\tilde{M}}_k})(x)$$ (2)

Residual Deformation Computation

Similarly to [4], the next step consists in averaging the T_Ĩl←M̃k into a transformation T̄_k and apply its inverse to M_k+1 to get the new reference M̃_k+1 = M_k+1 ○ ${\overline{T}}_k^{-1}$. However, we are averaging transformations using spatially variable weights w̄_l,k(x). To take this into account and ensure that T̄_k is a diffeomorphism, we introduce a generalization of the Log-Euclidean (LE) polyaffine transformation to diffeomorphisms, as suggested in [13]. The polydiffeomorphism construction is based on the LE framework for diffeomorphisms [11], allowing to compute operations easily while staying on the manifold of diffeomorphisms. T̄_k is then built by integrating between time 0 : x(0) = x and time 1 : x(1) = T̄_k(x) the following Ordinary Differential Equation (ODE): $\dot{x}={\sum }_{l=1}^N{\overline{w}}_{l,k}(x)\text{log}\left(T_{{\tilde{I}}_l\leftarrow {\tilde{M}}_k}^{(k)}\right)(x)$. Similarly to the LE polyaffine framework, T̄_k and ${\overline{T}}_k^{-1}$ are expressed respectively as the exponential of the right hand side of the ODE, and the exponential of its opposite.

3 Evaluation Methodology

To evaluate our method, we have used a database of 105 CT images of patients delineated for head and neck radiotherapy following the guidelines provided in [7]. Segmented structures included 12 structures: lymph nodes II, III and IV, parotids and sub-mandibular glands on each side as well as the spinal cord and the brainstem. On this database, we have repeated a Leave-One-Out approach, each time picking out one patient from the dataset of images. The average atlas is then built from the remaining images. We used this framework to compare two segmentation methods: the average atlas-based segmentation, and the locally most similar image based segmentation. The Frankenstein’s creature was built by defining on the average atlas a region of interest for each structure. This gives a total of 12 selected images, combined together into a single composite patient. This image is then registered on the left-out patient to get its segmentation.

The results were then compared to the manual delineations of the left-out patient using two voxel-based overlap measures: sensitivity (rate of true detection of the structure) and specificity (rate of true detection of the background). As they were delineated for radiotherapy, some structures were not available. We have therefore used the Leave-One-Out evaluation on a subset of 58 patients which had 8 or more manual delineations. Finally, the separation between some structures (lymph nodes, brainstem and spinal cord) are made on an arbitrary axial plane, based on possibly moving anatomical landmarks. This may lead to errors in the separations of the automatic segmentations and artificially low quality measures for all methods. We addressed this by evaluating together the brainstem and spinal cord, and by grouping the lymph nodes on each side.

4 Results

4.1 Qualitative Evaluation

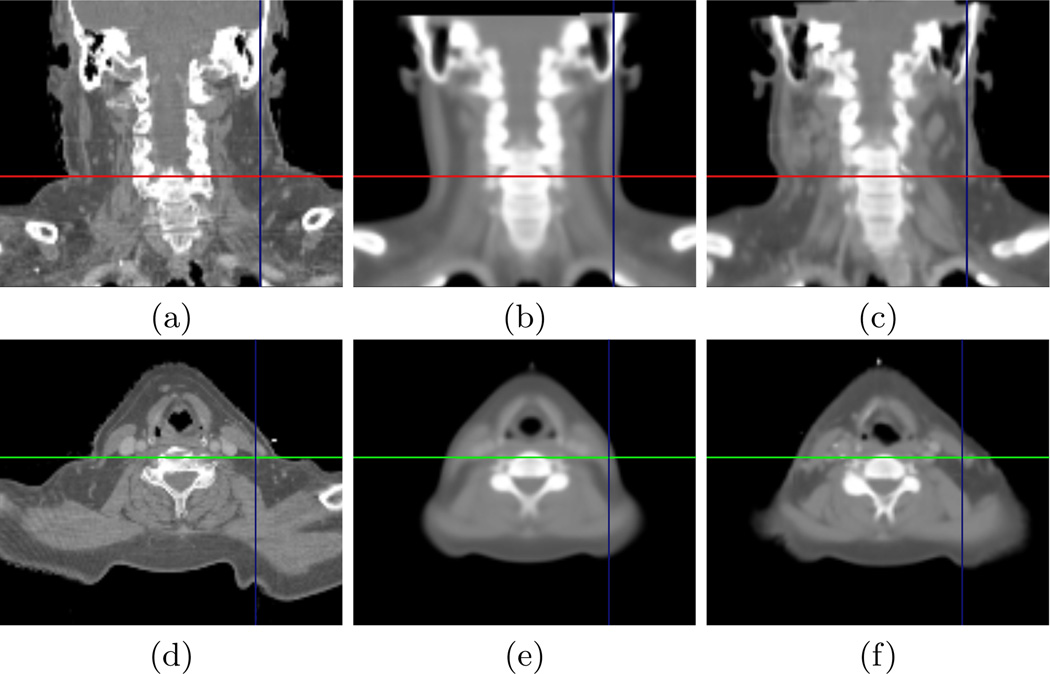
We first present in Fig. 1 the visual comparison of the average atlas and locally most similar image for one patient. This example illustrates very well that the average atlas anatomy may be significantly different from the patient after a global registration. This may result in registration discrepancies and in erroneous segmentations. This is particularly visible in the lymph nodes areas (see axes in the images) where the patient is much more corpulent than the atlas. The composite patient is much closer visually to the patient. The deformations between these two images will therefore be easier to recover and this will contribute to minimize the registration errors.

Fig. 1. Example of Computed Piecewise Most Similar Image.

Comparison between the patient image (a), (d) ; the average atlas (b), (e) and the locally most similar image (c), (f). All images are globally registered on the patient’s image.

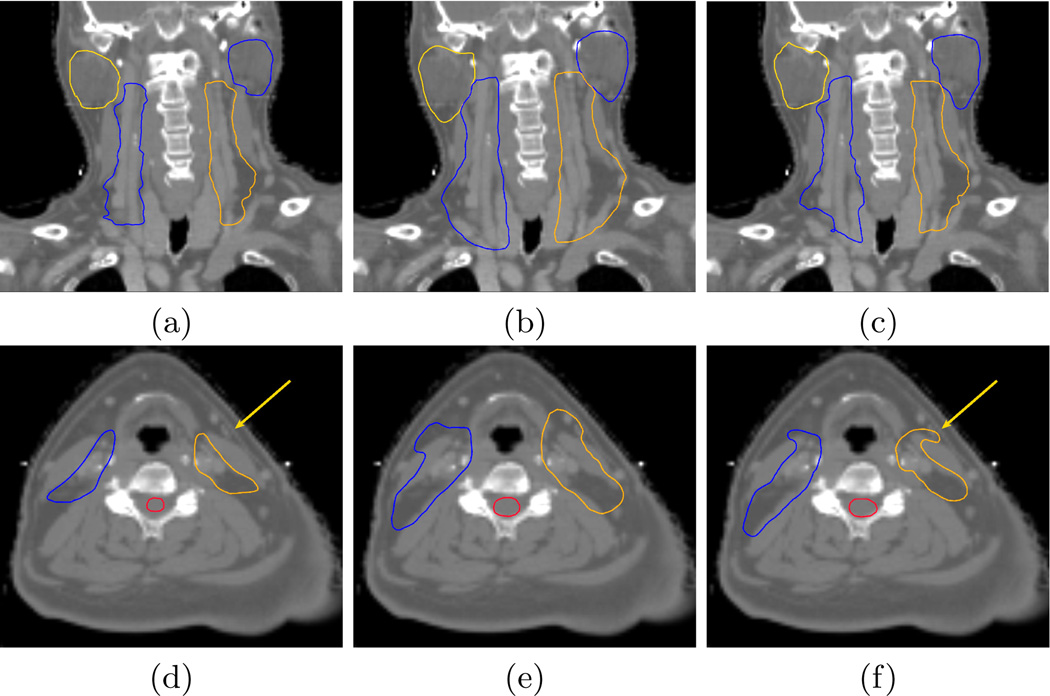
We then present in Fig. 2 the qualitative evaluation of the segmentation results, using the Leave-One-Out framework. This figure first shows that the atlas-based segmentations (images (b,e)) are overly large when compared to the manual ones. This is due to the inter-expert segmentation variabilities when creating the average segmentations, resulting in overly large segmentations in the atlas itself. This over-segmentation almost disappears using our approach. Only a single manual segmentation is indeed used for each structure, leading to more accurate segmentations, particularly on the lymph nodes areas. Finally, there are still differences in some regions (see arrow in image (f)). These differences are due to the local specificities of the selected manual segmentation, induced by the inter-expert segmentation variability.

Fig. 2. Qualitative atlas and piecewise most similar image based segmentation results.

Comparison between the manual segmentations (a), (d) ; the atlas-based segmentations (b), (e) and the piecewise most similar image segmentations (c), (f).

4.2 Quantitative Evaluation

We finally present in this section the quantitative evaluation of the results using the Leave-One-Out framework described in section 3. We present in Table 1 the average quantitative results (sensitivity and specificity) computed using the Leave-One-Out framework on 58 patients. We also indicate the number of structures on which each average was performed. The patients in the database were indeed not totally segmented manually and we therefore computed the quantitative values for the available structures.

Table 1. Quantitative Segmentation Results Comparison.

Sensitivities (Sens.), specificities (Spec.) and their standard deviations for atlas-based and locally most similar image (Frankenstein) based segmentation (see text).

	Atlas		Frankenstein		Patients
	Sens. ± StD	Spec. ± StD	Sens. ± StD	Spec. ± StD
Lymph Nodes (L)	0.930 ± 0.051	0.607 ± 0.070	0.692 ± 0.097	0.813 ± 0.072	53
Lymph Nodes (R)	0.923 ± 0.045	0.630 ± 0.078	0.675 ± 0.113	0.832 ± 0.074	46
Spinal Cord	0.938 ± 0.044	0.730 ± 0.065	0.773 ± 0.093	0.867 ± 0.079	47
Left Parotid	0.885 ± 0.072	0.691 ± 0.089	0.700 ± 0.172	0.813 ± 0.074	22
Right Parotid	0.879 ± 0.085	0.703 ± 0.078	0.684 ± 0.107	0.856 ± 0.050	19

This table shows an important improvement of the specificity measure in the locally most similar method with respect to classical atlas-based segmentation. This confirms the observations made in the qualitative results as this measure increases as the over-segmentation of the structures with respect to the manual segmentations decreases. However, the sensitivity is lower in the locally most similar case. This is mainly due to the inter-expert segmentation variabilities illustrated in Fig. 2. Nevertheless, these results are very promising and show that the locally most similar image allows to obtain an atlas whose anatomy is close to the patient to delineate and to remove the over-segmentation.

5 Conclusion

We have presented a new method to select, up to an affine transformation, the locally most similar images associated to regions of interest predefined on a precomputed average atlas. This is based on the use of a Log-Euclidean distance between transformations obtained through atlas construction and the transformation to register the patient on the atlas. As the atlas is pre-computed, the selection method is very efficient, requiring only one non linear registration. We have then associated to this selection a novel framework to build from these images a composite patient to be used as a template for the patient segmentation.

This method was validated by comparing it to atlas-based segmentation on a subset of 58 CT images among a database of 105 head and neck patients. The segmentations are not over-segmented anymore using our approach. This is seen both on qualitative and quantitative results (specificity). This method has a great interest and could also be applied to many other regions where large variabilities may be seen in the patients anatomies, such as the abdomen region.

We have seen in our experiments that the sensitivity results are corrupted by a large intra- and inter-expert segmentation variability. It is also partially responsible for the overly large segmentations in the average atlas. In the future, we aim at studying further this segmentation variability by computing locally, in the average atlas reference frame, the changes of each delineation, for example using the Staple algorithm [14]. This would be of great interest to reduce the variability inuence on the segmentation process.

Finally, we will study in the future other selection criterions, such as intensity based comparisons between the images, and compare their performance on the selection of the locally most similar image. We will also study how to combine these different criterions to obtain a very robust selection criterion.