Table 2.

Mean values of iPCF and iPNF estimated using: the population risk distribution F(R) assuming that the model is well calibrated; risks in a case–control study and known disease prevalence μ; observations of (R,Y) in the population

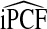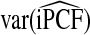								ARE
p†	iPCF true	R	CC	(R,Y)	R	CC	(R,Y)	CC/R	(R,Y)/R	(R,Y)/CC
α=6.55,β=124.45†
0.10	0.60	0.60	0.60	0.60	0	1.26	1.26	279.48	278.91	1.00
0.20	0.57	0.57	0.57	0.57	0	1.20	1.20	311.36	311.83	1.00
0.30	0.53	0.53	0.53	0.53	0	0.84	0.84	316.73	316.32	1.00
0.40	0.48	0.48	0.48	0.48	0	0.49	0.49	271.95	271.77	1.00
α=1,β=2.33‡
0.10	0.73	0.73	0.73	0.73	0.02	0.81	0.81	46.58	46.54	1.00
0.20	0.68	0.68	0.68	0.68	0.01	0.59	0.59	59.61	59.52	1.00
0.30	0.63	0.63	0.63	0.63	0.01	0.39	0.39	68.36	68.90	1.01
0.40	0.55	0.55	0.55	0.55	0	0.24	0.25	69.42	69.52	1.00
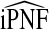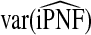								ARE
q†	iPNF true	R	CC	(R,Y)	R	CC	(R,Y)	CC/R	(R,Y)/R	(R,Y)/CC
α=6.55,β=124.45†
0.60	0.27	0.27	0.27	0.27	0.0014	0.44	0.44	311.04	310.85	1.00
0.70	0.22	0.22	0.22	0.22	0.0006	0.23	0.23	358.61	358.83	1.00
0.80	0.16	0.16	0.16	0.16	0.0003	0.10	0.10	353.88	353.58	1.00
0.90	0.09	0.09	0.09	0.09	0	0.02	0.02	506.42	506.83	1.00
α=1,β=19.0‡
0.60	0.19	0.19	0.19	0.19	0.01	0.49	0.49	58.48	58.39	1.00
0.70	0.16	0.16	0.16	0.16	0.01	0.27	0.27	53.43	53.46	1.00
0.80	0.12	0.12	0.12	0.12	0.0002	0.15	0.15	77.24	77.47	1.00
0.90	0.07	0.07	0.07	0.07	0	0.05	0.05	91.55	91.58	1.00
α=0.3,β=5.7‡
0.50	0.12	0.12	0.12	0.12	0.01	0.29	0.30	20.92	21.71	1.04
0.60	0.11	0.11	0.11	0.11	0.01	0.23	0.23	19.70	20.19	1.02
0.70	0.10	0.10	0.10	0.10	0.01	0.19	0.19	26.88	26.77	1.00
0.80	0.08	0.08	0.08	0.08	0	0.11	0.11	27.62	27.53	1.00
0.90	0.05	0.05	0.05	0.05	0	0.05	0.05	46.03	45.81	1.00

Results are based on 500 simulations for each set of parameters (α,β) for the beta distribution and values of q and p. Each simulation has N=10 000 samples with μ=0.05. AREs are computed as the ratio of the influence function-based variances.

ARE = asymptotic relative efficiency, the ratio of the influence functions-based variances CC/R=var(T_CC)/var(T_R), (R,Y)/R=var(T_(R,Y))/var(T_R), (R,Y)/CC=var(T_(R,Y))/var(T_CC), where T=PCF or T=PNF respectively.

^†AUC=0.63.

^‡AUC=0.79.

^§AUC=0.92.