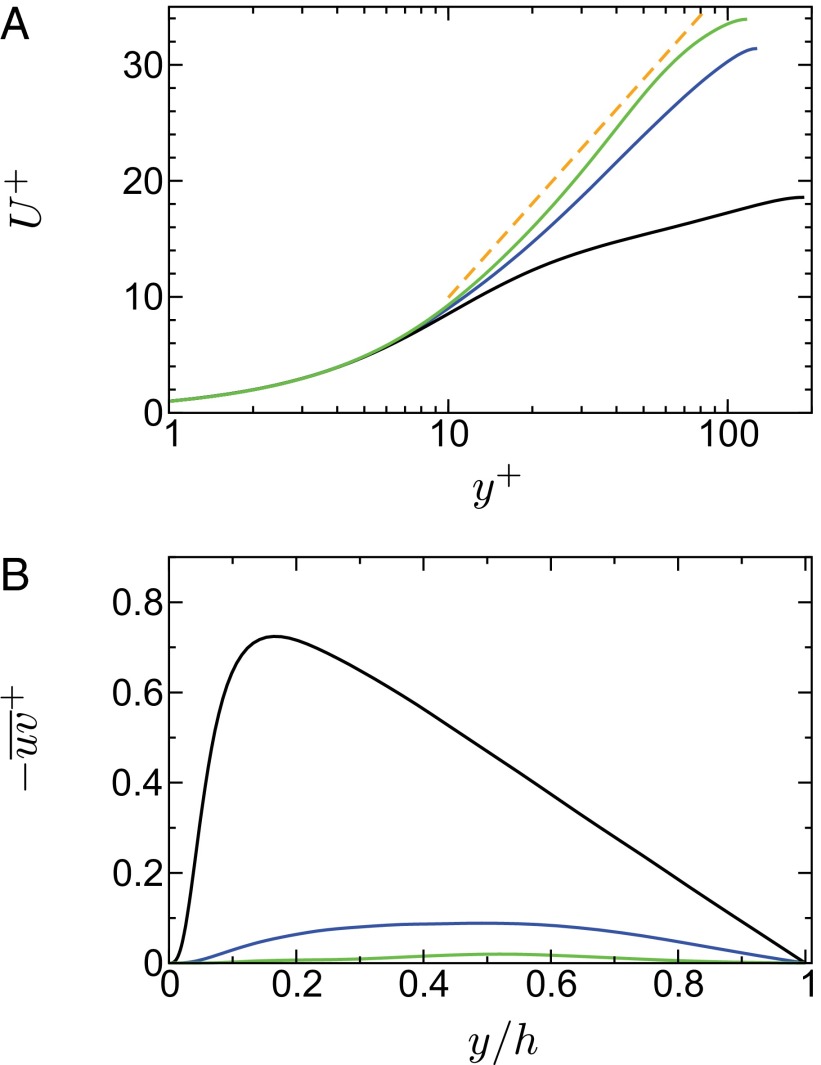
Fig. 5.
Profiles of turbulence statistics at the highest simulated 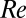 with the addition of a higher
with the addition of a higher 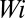 simulation. For FENE-P fluids (see SI Text),
simulation. For FENE-P fluids (see SI Text),  leads to a universal form of the polymer tensor closely related to the MDR asymptotic state. Mean velocity profiles in the typical log-linear representation are shown, where the mean velocity
leads to a universal form of the polymer tensor closely related to the MDR asymptotic state. Mean velocity profiles in the typical log-linear representation are shown, where the mean velocity  and the distance from the wall
and the distance from the wall 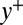 are normalized by skin-friction velocity
are normalized by skin-friction velocity 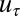 and kinematic viscosity (A) vs. profiles of Reynolds shear stress,
and kinematic viscosity (A) vs. profiles of Reynolds shear stress, 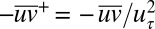 , as a function of the distance from the wall normalized by the channel half-height h (B). Statistics are shown for Re = 6,000; solid blue line, Wi = 100; solid green line, Wi = 700; solid black line, Newtonian turbulent flow. (A) Virk log-law (6) is denoted by the dashed orange line. The Virk mean velocity profile is a best fit of high
, as a function of the distance from the wall normalized by the channel half-height h (B). Statistics are shown for Re = 6,000; solid blue line, Wi = 100; solid green line, Wi = 700; solid black line, Newtonian turbulent flow. (A) Virk log-law (6) is denoted by the dashed orange line. The Virk mean velocity profile is a best fit of high 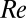 data. The assumption of the existence log-law at a low
data. The assumption of the existence log-law at a low 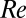 was recently shown (39) to fail at a low to moderate
was recently shown (39) to fail at a low to moderate 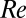 (at least up to
(at least up to 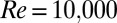 ). The agreement of
). The agreement of 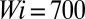 is consistent with previous MDR simulations and experiments. (B) Experiments of Warholic et al. (41) at MDR observe negligible Reynolds shear stress.
is consistent with previous MDR simulations and experiments. (B) Experiments of Warholic et al. (41) at MDR observe negligible Reynolds shear stress.