Interlimb differences of directional biases for stroke production

Abstract

Directional preferences during center-out horizontal shoulder–elbow movements were previously characterized for the dominant arm. These preferences were attributed to a tendency to actively accelerate one joint, while exploiting largely passive motion at the other joint. Since the non-dominant arm is known for inefficient coordination of inter-segmental dynamics, here we hypothesized that directional preferences would differ between the arms. A center-out free-stroke drawing task was used that allowed freedom in the selection of movement directions. The task was performed both with and without a secondary cognitive task that has been shown to increase directional biases of the dominant arm. Mirror-symmetrical directional preferences were observed in both arms, with similar bias strength and secondary task effects. The preferred directions were characterized by maximal exploitation of interaction torques for movement production, but only in the dominant arm. The non-dominant arm failed to benefit from interaction torques. The results point to a hierarchical architecture of control. At the higher level, a movement capable to perform the task while satisfying preferences in joint control is specified through forward dynamic transformations. This process is mediated for both arms from a common neural network adapted to the dominant arm and, specifically, to its ability to exploit interaction torques. Dynamic transformations that determine actual control commands are specified at the lower level of control. An alternative interpretation that strokes might be planned evenly across directions, and biases emerge during movement execution due to anisotropic resistance of intrinsic factors that do not depend on arm dominance is also discussed.

Introduction

Neural control of arm movement direction has been a topic of research for decades. The debates were initiated by a finding that firing rates of single motor neurons in motor cortex are tuned to movement direction (Georgopoulos et al. 1982, 1986) and that activity of populations of these neurons reliably represents movement trajectory (Schwartz 1994). Later studies suggested that the anisotropic intersegmental dynamics of the arm may substantially influence control of movement direction (Sabes and Jordan 1997; Scott et al. 2001).

Our recent findings support the latter hypothesis, suggesting that intersegmental dynamics causes directional preferences of arm movements (Dounskaia et al. 2011; Goble et al. 2007). We used a center-out free-stroke drawing task in which participants produced strokes with the fingertip from the center of a circle to the perimeter. The instruction was to produce strokes equally across different directions, selecting directions in a random order. Although this instruction encouraged the uniform distribution of movement directions, participants demonstrated consistent biases, frequently selecting certain directions and avoiding some other directions. Two directions represented the major preferences: diagonal movements to and away from the shoulder (this preferred direction will be further referred to as “longitudinal” diagonal) and movements along the other diagonal (further addressed as “transverse” diagonal), also in both directions.

The optimal control framework was employed to determine factors contributing to the revealed biases. Seven cost functions were formulated, the optimization of which could cause the biased selection of movement directions (Goble et al. 2007). Three of these cost functions represented a possible tendency to maximize smoothness of movement trajectory and to minimize total muscle torque (MUS) and change in MUS. The other four cost functions represented a possible tendency to minimize effort for control of anisotropic effects of intersegmental kinematics and dynamics of the limb. The best fit to the observed directional preferences was provided by two cost functions that represented a tendency to actively rotate one joint (either the shoulder or elbow) and to allow interaction torque (INT, a passive torque emerging from intersegmental dynamics of the limb) to generate motion at the other joint. Specifically, the preferred movements along the longitudinal diagonal were performed with active shoulder motion and predominantly passive elbow motion. Movements along the transverse diagonal were produced by active elbow motion and largely passive shoulder motion.

The tendency to minimize active coordination of INT obtained further support from our later studies. Dounskaia and Goble (2011) used a free-stroke drawing task during which movements were not limited to a circular space, and horizontal strokes were initiated anywhere in front of the subject. Directional biases were again evident, although in intrinsic and not extrinsic space. As in the previous study, the optimization approach pointed to the two INT cost functions as the best predictors of the directional biases. Additionally, Dounskaia et al. (2011) tested the dependence of the directional biases on a number of experimentally manipulated factors that could influence selection of movement direction. The availability of visual information, rate of stroke production, and attention were manipulated. While the effect of the first two factors was minor, distraction of attention with a secondary task markedly strengthened the directional biases without changing the major preferred directions. This finding supported the interpretation that directional biases emerged predominantly due to a tendency to minimize control effort required for coordination of INT at the subordinate joint.

The preference to select movement directions in which minimal active control of INT is required suggests that directional biases emerge during movement planning that takes into account the dynamic efficiency of the intended movement. Alternatively, directional biases might arise downstream to the direction selection process, during movement execution. According to this idea, intrinsic factors, such as INT, may cause deviations from the planned directions. For instance, errors in MUS generation may cause deviations from the directions that require INT suppression but not in the directions in which MUS does not interfere with INT.

Here, we will distinguish between the two alternative interpretations by comparing directional biases between the dominant (D) and non-dominant (ND) arm. The directional preferences were observed in our studies in movements of the dominant arm. Sainburg and colleagues have found that unlike the D arm, the ND arm is inefficient in coordinating intersegmental dynamics, such as INT (Bagesteiro and Sainburg 2002; Sainburg 2002; Sainburg and Kalakanis 2000). The need to specify INT control during movement planning may therefore influence the selection of movement direction in the ND arm differently compared with the D arm, thus resulting in different directional biases. The alternative interpretation of directional biases as deviations from preplanned directions caused by the influence of intrinsic factors during movement execution predicts no differences between the arms because such factors do not depend on arm dominance. By comparing directional biases exhibited by the two arms, we should thereby be able to determine at what level of the planning process the directional biases arise.

This goal was pursued by testing directional biases during performance of the free-stroke drawing task with horizontal movements of the D and ND arm. Attention manipulation with the use of a cognitive secondary task was also included, taking into account the finding of Dounskaia and Goble (2011) that this manipulation markedly enhanced directional biases in the D arm. It was expected that differences in directional biases between the two arms would be more pronounced during simultaneous performance of the secondary task than without it.

Materials and methods

Subjects

Ten neurologically intact right-handed adults (2 males and 8 females, 22 ± 2 years of age) were recruited from the university community to participate in this study. Subjects signed informed consent prior to participation. The institutional review board at Arizona State University approved the experimental protocol.

Procedure and design

The experimental procedure was similar to that used by Dounskaia et al. (2011) and by Goble et al. (2007) except for that movements were produced with the D and ND arm. Subjects sat at a table, the height of which was adjusted to provide arm movements approximately in the horizontal plane at the shoulder level. The upper arm segments were supported in slings suspended from the ceiling to reduce muscle effort for gravity compensation. Subjects produced strokes by either the D or ND arm, sliding the tip of the index finger along the table surface. The finger tip was wrapped with Micropore™ paper tape to reduce friction with the table. The arm movements were performed through flexion/extension of the elbow and shoulder. Motion at the trunk was prevented by restraining the torso between the table edge and the chair back. The wrist was immobilized with a splint. The index finger was splinted in a fully extended position to prevent motion of the fingertip relative to the hand.

The task consisted of the performance of a series of straight fingertip strokes from the center to the perimeter of a circle depicted on the table surface. The circle had a radius of 15 cm. The location of the center was adjusted to the initial position of the arm performing the task. The initial arm position was determined by the shoulder and elbow joint angles of φ = 30° and θ = 100°, respectively. The joint angles were defined relative to the longitudinal axis of the proximal segment (Fig. 1). The usage of joint angles to define the initial positions of the arms assured similar intersegmental dynamics conditions across subjects. The initial joint angles were chosen to allow movements from the center to the circle perimeter in all directions with minimal elastic forces that may arise at the anatomical limits of joint rotations.

Fig. 1.

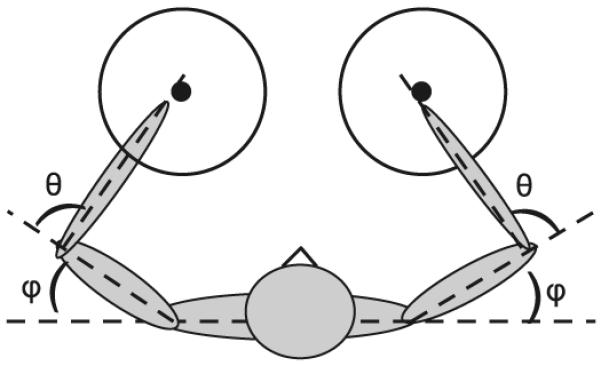
Experimental setup and joint angles. Subjects performed center-out movements with either the D or ND arm within a circular workspace specified for each arm. The locations of the two circle centers were defined by shoulder and elbow joint angles of θ = 30° and φ = 100°, respectively. Positive values of θ and φ corresponded to flexion at both the elbow and shoulder joints

No specific accuracy of reaching the perimeter was required during the production of center-out strokes. Fingertip motion did not leave any visible traces on the table. Upon completing each stroke, subjects moved the fingertip along the table surface back to the circle center to initiate a subsequent stroke. The instruction was to select direction of each center-out stroke randomly and to produce strokes in as many different directions as possible. Thus, the instruction encouraged the uniform distribution of movement directions. Deviations from the uniform distribution consistent across subjects would indicate inherent directional biases.

The free-stroke drawing task was first performed with the D arm and then with the ND arm. Subjects were instructed to produce strokes at 1.5-Hz frequency guided by a metronome. Each arm performed the task first without any secondary task and then simultaneously with a secondary task. The secondary task consisted of counting out loud, while continuously reducing by three, a number given by the experimenter at the trial start. Ten fifteen-second trials were performed in each condition, each including the production of series of strokes. Two practice trials were provided prior to the initiation of data recording in each condition. If necessary, verbal feedback was provided to discourage a specific order of movement directions, such as clockwise or counterclockwise stroke sequences, and to emphasize the need to select movement directions randomly.

Prior to performance of the task with each arm, position of the arm while touching the circle center was recorded for 15 s. These data were later used for the identification of the circle center location.

Data collection and analysis of directional biases

Arm movements were recorded with an OPTOTRAK® (Northern Digital Inc., Waterloo, Ontario, Canada) three-dimensional optoelectronic system. Seven infrared emitting diodes (IREDs) were positioned on the trunk and the two shoulders, elbows, and index fingernails. Time varying position data were recorded at a sampling rate of 200 Hz. The collected data were filtered with a 7-Hz low-pass 4th-order Butterworth digital filter.

Center-out strokes were identified with the use of minima of fingertip marker velocity. Pairs of the consecutive minima were interpreted as the beginning and the end of a stroke if the first minimum occurred within a 4-cm radius from the circle center and the next minimum took place at least at 12-cm distance from the circle center. The initial and final stroke portions during which velocity was lower than 3% of its peak value were removed from the analyzed trajectories. Only strokes entirely produced in the horizontal plane along the table surface as demonstrated by the z-axis component of the fingertip marker were considered. Additionally, strokes were required not to have portions characterized by curvature exceeding 50 m⁻¹. This requirement was introduced to prevent inclusion of sharp turns associated with reversals in movement trajectory. Curvature was computed as $C=\mid \stackrel{.}{x}\cdot \ddot{y}-\ddot{x}\cdot \stackrel{.}{y}\mid ∕{({\stackrel{.}{x}}^2+{\stackrel{.}{y}}^2)}^{3∕2}$, where $\stackrel{.}{x}$, $\stackrel{.}{y}$ and $\ddot{x}$, $\ddot{y}$ represent the first and second derivatives of the (x, y) position data, respectively. Finally, only strokes that contained a minimum of 100 ms of data and a minimum length of 12.5 cm were considered to prevent inclusion in the analysis of shortened and incomplete strokes; 98.6% of all strokes were included in the analysis.

The angular orientation of each stroke was determined with the use of the line connecting the location of the end point at stroke initiation and termination. The 0° orientation was assigned to movements performed in the mediolateral direction away from the body midline (to the right for the D arm and to the left for the ND arm). For both arms, 90° was associated with strokes drawn along the anterioposterior direction away from the subject.

For each subject, the stroke orientation data generated during ten trials in each experimental condition were combined to build individual directional histograms. The histograms were produced by placing the orientation data into 72 bins, each of 5° width. These histograms were smoothed using a standard normal kernel smoothing function having a window width of 5°, yielding a probability density estimate for each orientation (Bowman and Azzalini 1997). For visualization purposes, each individual histogram was normalized to its maximal value. It is important to note that although the polar representation of histograms visualized directional biases, it distorted the histogram's image, increasing the angular scale for histogram levels that are further from the center. For this reason, the polar representation was used only for the visualization of histograms, while a linear representation of the histograms was used for numeric analyses.

Each individual histogram was analyzed to identify statistically significant peaks that were interpreted as directional biases. The multimodal distributions within the individual histograms were analyzed with a mode existence test (Minnotte 1997; Minnotte and Scott 1993). A detailed description of the application of this test to directional histograms is presented by Goble et al. (2007). Briefly, this test revealed whether each peak identified in the directional histogram was either an artifact of the sample or a true feature of the population. Due to the conservative nature of tests for multimodality, peaks were considered significant at P ≤ 0.15 (Izenman and Sommer 1988; Minnotte 1997). The mode existence test provided the direction and bounds of each significant peak.

To evaluate the dependence of directional biases on the arm and the secondary task, bias strength was assessed in each directional histogram f(x) as the deviation of f(x) from its mean value M. Here, x represents movement direction (0° < x < 360°) and M represents the uniform distribution that would be obtained if the stroke directions were distributed evenly. After applying the smoothing procedure, x varied with an increment 0.1° across 3,601 directions. Since directional biases were represented by histogram peaks that exceeded M, and values f(x) < M were limited by 0 (which could distort the evaluation of bias strength), only directions x_i (i = 1,…,N) in which f(x_i) > M were included in the computation. The bias strength was computed as:

$$\text{BS}=\frac{1}{N}\frac{1}{M}\sum _{i=0}^N\left(f\right(x_i)-M),$$ (1)

where the normalization coefficients 1/N and 1/M were used to allow the comparison of bias strength across conditions and subjects. Computed in this way, bias strength is higher for directional histograms characterized by larger deviation of their peaks from the uniform distribution.

Joint torques

Torques at the joints were computed from angular velocity and acceleration time series obtained by differentiation of shoulder (φ) and elbow (θ) joint angles that were calculated from the IRED position data. Torque computations were performed with the use of two-joint equations of motion presented by Dounskaia et al. (2002) as torque definition II. Namely, INT, MUS, and net torque (NET) were computed for each joint. INT represents the passive rotational effect attributed to reaction forces at the joints due to motion of the adjacent limb segments. MUS represents the effect of muscle forces on joint rotation. NET reflects the net effect of INT and MUS, i.e., NET = INT + MUS. The influence of gravitation was not considered because arm movements were performed in the horizontal plane. Anthropometric measurements including limb segment inertia, mass, and center of mass exploited for torque calculations were estimated from regression equations using the height and weight of each subject (Chaffin and Andersson 1984).

Cost functions

The calculated torques were used to compute the two cost functions, optimization of which accounted for directional biases in the D arm in our previous studies (Dounskaia and Goble 2011; Dounskaia et al. 2011; Goble et al. 2007):

$$I_{\text{INTE}}=\frac{1}{T_1-T_0}\sum _{t=T_0}^{T_1}\frac{\mid {\text{INTE}}_t\mid }{\mid {\text{INTE}}_t\mid +\mid {\text{MUSE}}_t\mid },$$ (2)

$$I_{\text{INTS}}=\frac{1}{T_1-T_0}\sum _{i=T_0}^{T_1}\frac{\mid {\text{INTS}}_t\mid }{\mid {\text{INTS}}_t\mid +\mid {\text{MUSS}}_t\mid },$$ (3)

Here, T₀ and T₁ are the time moments of the beginning and the end of the stroke, INTE and INTS are interaction torques, and MUSE and MUSS are muscle torques at the elbow and shoulder at each moment of time T₀ ≤ t ≤ T₁. These cost functions represented a tendency to produce predominantly passive motion either at the elbow (I_INTE) or at the shoulder (I_INTS) by generating low MUS compared with INT. Each cost function varied between 0.0 and 1.0 with 1.0 being the optimal value representing completely passive joint motion performed with MUS = 0. A movement was considered optimized if the value of the corresponding cost function was greater than 0.6. This threshold distinguished strokes during which motion at the corresponding joint was predominantly passive, i.e., it was generated through a larger contribution of INT compared with MUS.

Directional histograms of strokes optimized according to each cost function were computed as the percent of optimized strokes relative to the total number of strokes in each direction. Contribution of a cost function to directional biases was revealed if a peak of the corresponding histogram coincided with one of the preferred directions represented by peaks of the directional histogram of all strokes.

Statistical analyses

Statistical analyses were used to assess the difference between the D and ND arm and the effect of the secondary task on characteristics of stroke production, directional biases, and contribution of I_INTE and I_INTS to them. A 2 × 2 (arm × task) ANOVA with repeated measures on both variables was applied to data obtained from the D and ND arm without and with the secondary task. Characteristics analyzed were the number of produced strokes, rate of stroke production, stroke length and curvature, bias strength, the percentage of strokes optimized in terms of I_INTE and I_INTE, and the percentage of non-optimized strokes, i.e., strokes that were not optimized by any of the two cost functions. The level of significance was set at 0.05.

Results

Characteristics of strokes

Strokes produced in all directions were typical point-to-point center-out movements. The number of produced strokes, rate of stroke production, and stroke length averaged across subjects for each arm without and with the secondary task are shown in Table 1. Even though the stroke production was paced by the metronome, the number of strokes and the rate of stroke production were higher in the D arm compared with the ND arm [F(1, 9) = 18.1, P<0.01 and F(1, 9) = 18.1, P<0.01, respectively]. The secondary task effect and the interaction were not significant for both characteristics (P>0.1). No significant effect of the arm and/or task was found for stroke length.

Table 1.

Mean characteristics of stroke production

	D arm		ND arm
	Without ST	With ST	Without ST	With ST
Stroke number*	21.7 ± 0.7	21.9 ± 1.7	19.8 ± 2.7	21.1 ± 1.2
Stroke rate (per sec)*	1.4 ± 0.04	1.5 ± 0.11	1.3 ± 0.18	1.4 ± 0.08
Stroke length (cm)	15.2 ± 5.1	15.3 ± 5.5	15.2 ± 4.6	15.2 ± 5.6
Stroke curvature**	0.037 ± 0.006	0.037 ± 0.004	0.047 ± 0.008	0.045 ± 0.007

^*significant arm effect (P < 0.01)

^**significant arm effect (P < 0.001)

Since previous research reported that trajectories of point-to-point movements performed by the ND arm were more curved than trajectories of the D arm (Bagesteiro and Sainburg 2002; Sainburg and Kalakanis 2000), we also assessed stroke curvature as deviation of the hand path from linearity (Bagesteiro and Sainburg 2002). The results are in Table 1. Consistent with the previous findings, strokes performed with the ND arm were more curved than strokes performed by the D arm [F(1, 9) = 22.4, P<0.001]. The secondary task effect and the interaction were not significant (P>0.1).

Directional biases

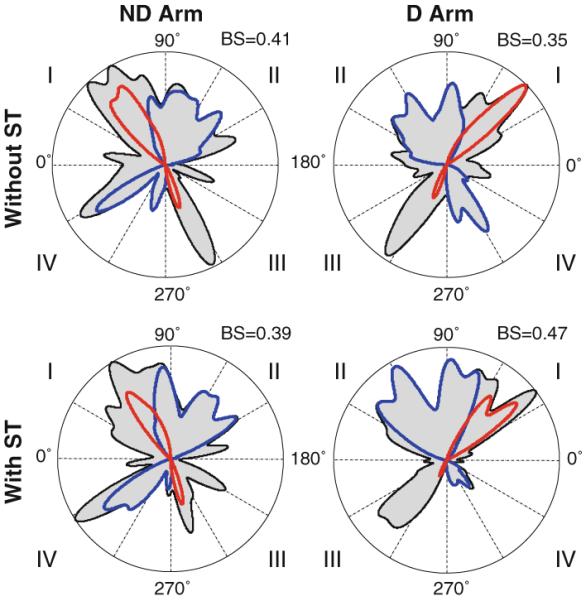
Figure 2 gives an example of strokes produced by a representative subject with each arm without (Fig. 2a, b) and with the secondary task (Fig. 2e, f). Each plot combines strokes produced in all 10 trials. Uneven distribution of the strokes across directions is apparent in all four plots. Distribution of stroke directions was assessed by building directional histograms of strokes produced by each subject in each condition. The plots in the bottom row of Fig. 2 demonstrate directional histograms of strokes shown in the top row. The color traces in these histograms are explained further when INT control is reported. Directional biases were revealed by peaks of the histograms. The dominant preference to produce strokes in the diagonal directions documented in our previous studies for the dominant arm (Dounskaia and Goble 2011; Goble et al. 2007) is apparent for both arms in both secondary task conditions. Furthermore, Fig. 2 shows that the directional preferences in the D and ND arm were mirror symmetrical.

Fig. 2.

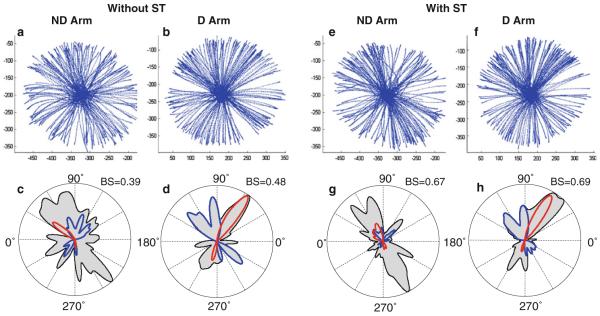
An example of strokes and corresponding circular histograms obtained from a representative subject. Data obtained from the D and ND arm without and with the secondary task are shown. The histograms represented by the contours of the gray areas demonstrate the frequency of stroke production in each direction for each subject. Peaks of these contours represent preferred directions. Bias strength (BS) is shown for each histogram. The histograms are overlapped with traces, representing the directional histograms of strokes optimized according to I_INTE (blue) and I_INTS (red). If a color trace closely follows a peak of the gray area, this indicates that the majority of strokes in this preferred direction were optimized with respect to the corresponding cost function. Here and in the other histograms, 0° denotes the lateral direction away from the body midline and 90° denotes the anterior direction away from the body

The preference to move in the diagonal directions and mirror symmetry of the preferred directions in the D and ND arm were common across subjects. This was shown by the analysis of statistically significant peaks of the individual histograms. Average, 4.4 ± 0.9 statistically significant peaks were identified in each directional histogram with no difference between the arms and no effect of the secondary task (P>0.1). Directional histograms of the statistically significant peaks detected across all subjects in each arm and task condition are shown in Fig. 3. The major peaks of the four histograms were in the diagonal directions, confirming that the majority of the peaks were diagonal. The preferences to produce strokes in the diagonal directions are also apparent in group histograms built for directions of strokes produced by all subjects in each condition (Fig. 4).

Fig. 3.

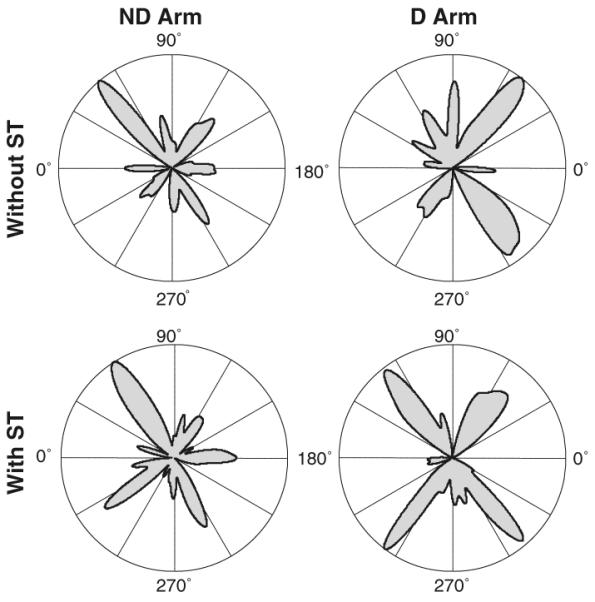
Directional histograms of statistically significant peaks detected in all individual directional histograms of strokes produced with the D arm (the right column) and ND arm (the left column) without (the top row) and with (the bottom row) the secondary task. The orientation of the major peaks in each panel in the diagonal directions demonstrates that peaks of individual histograms were also mainly oriented in these directions

Fig. 4.

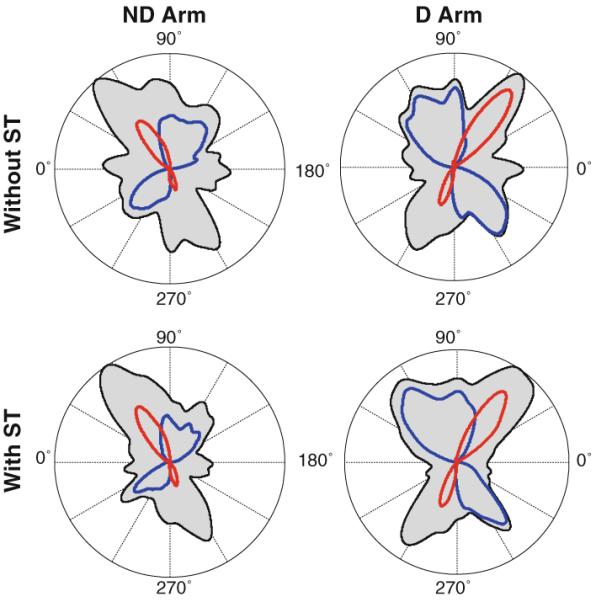
Group histograms of stroke directions obtained with the D arm (the right column) and ND arm (the left column) without (the top row) and with (the bottom row) the secondary task. The blue and red contours show group histograms of strokes optimized in terms of I_INTE and I_INTS

Visual comparison of the group histograms in Fig. 4 between the arms shows that the preferred directions were largely mirror symmetrical. This symmetry is even more apparent in Fig. 5 that shows linear representations of the group directional histograms plotted together for the D and ND arm in each secondary task condition. In this figure, the x-axis shows movement directions with respect to the body's midline with 0° denoting the lateral direction away from the body's midline and 90° denoting the direction away from the body. The correlation coefficient computed between the two group histograms was 0.79 in both secondary task conditions. Both were statistically significant (P<0.05), confirming that directional preferences in the D and ND arm were largely mirror symmetrical.

Fig. 5.

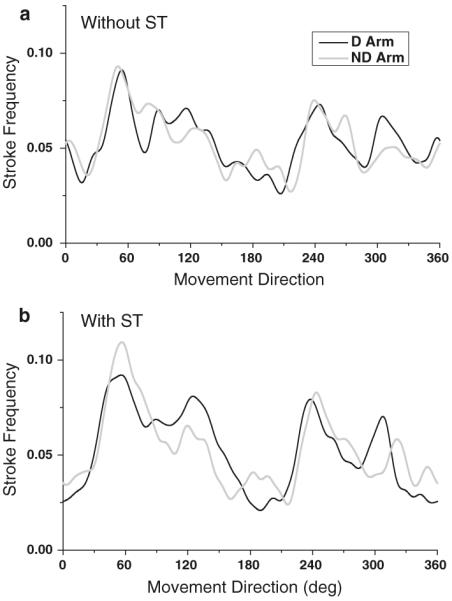
Linear representation of the group directional histograms. Each plot shows group histograms for the D and ND arm (a) without and (b) with the secondary task

The similarity of the directional biases in both arms was further tested by computing bias strength. Mean and SD values of bias strength are shown in Fig. 6. Bias strength was not statistically different between the arms. The secondary task caused similar increases in bias strength in the D and ND arm [F(1, 9) = 8.9, P<0.05]. The interaction was not significant (P>0.1).

Fig. 6.

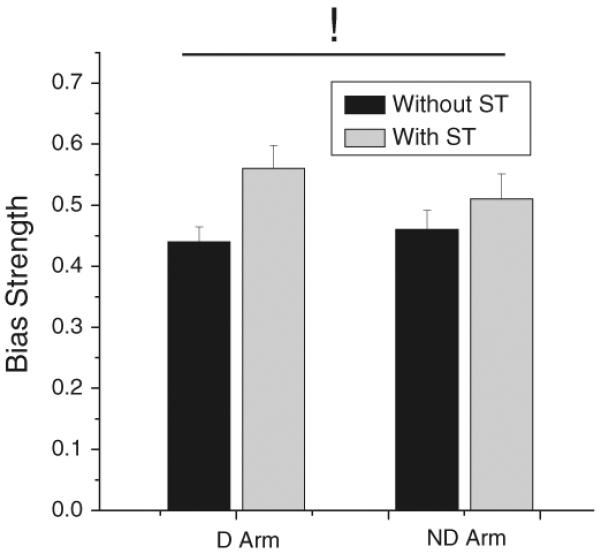
Effect of the arm and secondary task (ST) on the strength of directional biases. The secondary task significantly increased bias strength equally in both arms. The significant main effect of the secondary task is indicated by !

INT control in the preferred directions

In the previous studies of directional biases, the majority of strokes performed in the preferred directions with the D arm were optimized in terms of one of the two cost functions, I_INTE or I_INTS (Dounskaia et al. 2011; Dounskaia and Goble 2011; Goble et al. 2007). Longitudinal strokes were produced predominantly with active (due to MUS) rotation of the shoulder and largely passive (due to INT) elbow motion. Accordingly, the transverse strokes were produced predominantly with active elbow rotation and largely passive shoulder motion. The color contours overlaid with the directional histograms in Figs. 2 and 4 represent directional histograms of strokes optimized according to the cost functions I_INTE (blue) and I_INTS (red) for the D and ND arm in the two secondary task conditions. It is apparent from both figures that the results obtained for the D arm in the present study were similar to those in the previous studies. Strokes optimized according to I_INTE (blue) were performed approximately in the longitudinal direction, and strokes optimized according to I_INTS (red) were performed approximately in the transverse direction. The color traces were close to the border of the corresponding peaks of the gray areas, indicating that the majority of strokes performed by the D arm in these preferred directions were optimized according to one of the two cost functions.

In the ND arm, the directions of the color contours were mirror symmetrical to those in the D arm, and they also coincided with the directions of the major peaks of the directional histograms that signified preferred directions. However, the areas outlined by the color contours in Figs. 2 and 4 are much smaller in the ND arm compared with the D arm. This observation suggests that the strokes optimized in terms of I_INTE and I_INTS were fewer in the ND arm. Analysis of the percentage of strokes optimized by each cost function confirmed this observation (Fig. 7a, b). The percentage of strokes optimized in terms of each cost function, I_INTE and I_INTS, was significantly lower in the ND arm compared with the D arm [F(1, 9) = 8.0, P<0.05 and F(1, 9) = 5.1, P = 0.05, respectively]. The secondary task effect and the interaction were not significant for both cost functions (P>0.1). Since there can be some overlap between the blue and red contours, we also computed percentage of non-optimized strokes (strokes that were not optimized in terms of any of the two cost functions) with respect to the total number of strokes in each individual histogram (Fig. 7c). The percentage of non-optimized strokes was significantly higher in the ND arm compared with the D arm [F(1, 9) = 7.5, P<0.05]. Neither the main effect of the secondary task nor the interaction was significant (P>0.1). These results show that, unlike the D arm, the ND arm failed to efficiently exploit INT in the biased directions.

Fig. 7.

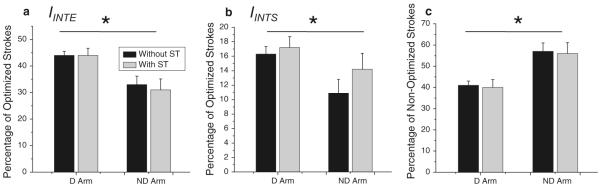
Optimization of I_INTE and I_INTS in the D and ND arm. The three panels demonstrate percentage of strokes (a) optimized in terms of I_INTE, (b) optimized in terms of I_INTS, and (c) not optimized in terms of any of the two cost functions. All three characteristics significantly depended on the arm (indicated by *) but not by the secondary task. The significant arm effect indicates that the ND arm exploited INT for joint rotation less efficiently than the D arm

The deficiency of the ND arm in INT control could also prompt a preference in this arm to perform single-joint elbow movements that require minimal INT control. Strokes performed with single-joint elbow movements are transverse diagonal, i.e., they are close to the strokes optimized in terms of I_INTS. Thus, even though the percentage of strokes optimized by I_INTS in the ND arm was lower compared with the D arm, the ND arm may have had a stronger preference to produce transverse strokes compared with the D arm.

Visual analysis of group histograms in Fig. 4 indeed suggests that the ND arm histograms were more stretched in the transverse-diagonal direction than the D arm histograms. We verified this difference by computing percentage of strokes produced by each arm in quadrants I and III that included the transverse strokes and in quadrants II and IV that included the longitudinal strokes. Neither the main effects of arm and secondary task nor the interaction was significant for both quadrant pairs (P>0.1). Visual analysis of individual histograms across all subjects accounted for the discrepancy of this statistical result with the shapes of the group histograms in Fig. 4. It was found that six of the ten subjects (S1, S5, S6, S7, S8, and S10) had more stretched histograms in the ND arm compared with the D arm (see the example of S7 in Fig. 2). However, the other four subjects (S2, S3, S4, and S9) did not show this tendency, as can be seen in Fig. 8 that shows the histograms obtained from S4. Thus, no consistent preference for the ND arm to perform movements predominantly through elbow rotation was found.

Fig. 8.

Individual directional histograms obtained from the D arm (the right column) and the ND arm (the left column) without (the top row) and with (the bottom row) the secondary task obtained in a subject who did not demonstrate a tendency to increase the number of strokes produces in quadrants I and III (i.e., strokes performed predominantly through single-joint elbow rotation in the ND arm. Bias strength (BS) is shown for each histogram. The quadrants are numbered for each arm relative to the body midline. Like in Fig. 2, the blue and red contours depict directional histograms of strokes optimized in terms of I_INTE and I_INTS, respectively

Discussion

The results obtained in the present study for directional biases in the D arm are in agreement with our previous findings (Dounskaia and Goble 2011; Dounskaia et al. 2011; Goble et al. 2007). Subjects demonstrated consistent preferences to produce strokes in the two diagonal directions. Movements in the preferred directions were predominantly optimized in terms of the cost functions I_INTE and I_INTS. This means that the majority of movements in the preferred directions were performed with minor contribution of MUS and major contribution of INT to rotation of one of the joints, either the elbow (along the longitudinal diagonal) or shoulder (along the transverse diagonal).

The leading joint hypothesis accounts for the results obtained for the D arm. This hypothesis offers an interpretation of joint control during multijoint movements (Dounskaia 2005, 2010; Dounskaia et al. 1998, 2002). According to this interpretation, the arm joints play different roles in movement production. One of the joints, either the shoulder or elbow, serves as the leading joint. Its MUS generates energy for motion of the entire limb because leading joint motion causes influential INT at the other (subordinate) joint. MUS at the subordinate joint controls the effect of INT generated by motion of the leading joint and modifies passive motion, producing required direction, accuracy, and other movement features. The precise regulation of INT with MUS at the subordinate joint may involve complex neural processes. The complexity of the subordinate joint control predicts a preference for movement directions that require minimal interference of MUS with INT at this joint. This prediction is represented by optimization of I_INTE when the subordiante joint is the elbow and by optimization of I_INTS when the subordinate joint is the shoulder. The results of this and our previous studies of directional biases in the D arm are consistent with this prediction, demonstrating the tendency to optimize I_INTE and I_INTS.

Unlike the transparent and expected results for the D arm, the results for the ND arm appear paradoxical. In contrast to our predictions that directional biases in the ND arm would differ from those in the D arm, the directional biases were similar in both arms. The most preferred directions were mirror symmetrical, and bias strength was the same in the arms. Furthermore, the secondary task equally increased bias strength in both arms. This effect of the secondary task was demonstrated for the D arm by Dounskaia and Goble (2011). It was consistent with the prediction of the directional biases from the complexity of neural processes involved in INT control at the subordinate joint. Cognitive load caused by the secondary task may decrease neural resources available for INT control, and therefore, it may increase the strength of the preference to avoid this control. The need for extra neural effort for INT control is supported by a finding that excitability of corticospinal projections to arm muscles is increased when INT needs to be suppressed as compared to movements during which INT assists joint motion (Gritsenko et al. 2011).

Thus, all characteristics of directional biases in the ND arm were similar to those in the D arm. However, the interpretation of these characteristics as a result of the tendency to minimize active control at the subordinate joint that was applicable for the D arm is problematic for the ND arm. The relative number of strokes optimized in terms of the cost functions I_INTE and I_INTS was substantially lower in the ND arm compared with the D arm, and therefore, the preference to rotate the subordinate joint predominantly passively, by INT, does not provide a convincing interpretation of the directional biases in the ND arm. The finding that the ND arm failed to exploit INT for movement production to the same extent as the D arm is consistent with the repeatedly demonstrated deficiency of the ND arm controller in coordinating INT with MUS (Bagesteiro and Sainburg 2002; Dounskaia et al. 2010; Sainburg 2002; Sainburg and Kalakanis 2000). The question is if the ND arm was not able to benefit from INT, why did it prefer the directions in which INT can be exploited?

We present two possible interpretations to this question related to the two possibilities discussed in the Introduction for the emergence of directional biases either during movement planning or during movement execution. The first interpretation supports the emergence of direction biases in the planning process, prior to arm selection. In fact, Sainburg has proposed that the hemisphere contra-lateral to the dominant arm is specialized for the specification of characteristics of movement trajectory, including planning of movement direction, for both arms (Sainburg 2005; Schaefer et al. 2009). Assuming that directional biases provide information about the selection of movement directions, our finding of symmetrical directional biases and equal increases in bias strength in both arms due to the secondary task is consistent with this organization. Our findings further suggest that the processes involved in planning of movement direction are adapted to the D arm controller, for both arms. In our study, the frequent selection of the diagonal directions was advantageous for the D arm controller that efficiently exploited INT. Since the ND arm preferred the mirror-symmetrical directions, the fact that coordination of INT in the ND arm has greater dynamic cost for these movements appeared to be neglected.

The suggested interpretation of the obtained results implies a hierarchical organization of the control process that includes at least two distinct levels. At the higher level, planning of movement direction is governed by principles predominantly associated with D arm control. At the lower level, generation of MUS for movement execution depends on specific properties of each arm's controller. A similar conclusion was made based on analysis of kinematics and dynamics of the D and ND arm during bimanual movements (Dounskaia et al. 2011; Wang and Sainburg 2009). For instance, Dounskaia et al. (2011) examined stability of bimanual coordination during drawing circles and ovals. Stability of a non-symmetrical coordination pattern was low, and it farther decreased with increases in cyclic frequency, which was consistent with findings of multiple previous studies (Franz 1997; Kelso 1984; Peper et al. 1995; Riek et al. 1992; Sherwood 1994; Swinnen 2002). An unexpected finding was that progressive deviations from the mirror-symmetrical coordination pattern were also observed. These deviations were caused by deficient control of INT that resulted in deformations of the drawn shapes in the ND arm but not in the D arm. These results argued for the two-level control architecture. The low stability of the non-symmetrical coordination pattern emerges due to interference between the arms at the level of planning of movement kinematics. The decreases in stability of the symmetrical pattern result from the differences between the arms at the level of MUS generation.

The hierarchical structure of the control process is consistent with the interpretation of this process as a sequence of inverse kinematic and dynamic transformations that eventually yield MUS capable to generate the desired movement (Atkeson 1989; Hollerbach 1982). However, our results suggest that the sequence of inverse transformations is a simplified model that does not adequately represent the control process. The interpretation of the observed directional biases with the tendency to simplify INT control implies that challenges associated with control of intersegmental dynamics are considered yet at the level of movement direction selection. This suggests that properties of limb's dynamics are taken into account at the level of planning of movement kinematics.

This inference is consistent with a hypothesis that in addition to inverse transformations, movement control also involves forward transformations of control commands to movement kinematics (Bhushan and Shadmehr 1999; Miall and Wolpert 1996; Wolpert et al. 1993). These transformations can be used for different purposes, including the prediction of the limb's state that will be acquired as a result of application of a specific control command and for the verification of correctness of inverse models. Our results support the use of forward transformations for the estimation of control effort and minimization of it. Importantly, they also suggest that the control commands used as the input signals for the forward models may not be exactly those actually sent to the muscles, but rather they are an estimate of the actual control commands. This conclusion follows from the understanding that control signals actually generated at the ND arm in the preferred directions did not optimize INT control, and hence, they were different from those used for the selection of optimized movement directions through forward transformations. Although the evidence for the difference between the outcome of the forward transformations and neural signals actually sent to the muscles was obtained for the ND arm only, this difference is likely present in the D arm as well, assuming that control of the D arm includes the same hierarchical levels as control of the ND arm.

An alternative explanation for the current findings is that the directional biases occur downstream in the control process to selection of movement direction. In short, directions are planned as an equal distribution around the circle. However, intrinsic factors poorly taken into account during movement planning cause biases in movement directions. For instance, if INT is underestimated, MUS generated at the subordinate joint would be insufficient to accurately offset INT. Another possibility is that there is a tendency to underproduce subordinate joint MUS. Both would result in the observed directional biases because strokes would deviate from the preplanned directions in which INT needs to be compensated with MUS but not from the directions in which no active interference with INT is required. Such intrinsic factors do not depend on arm dominance, and therefore, similar directional biases would emerge in the D and ND arm, as was observed in our experiment.

Multiple studies demonstrated that INT is predicted and muscular control is generated in consideration of this prediction (Gribble and Ostry 1999; Koshland and Hasan 1994; Latash et al. 1995). Straightness of the path to a target shows that the offset of INT with MUS is usually accurate, at least in the D arm. However, this does not exclude a possibility for a systematic underproduction of MUS for INT coordination when no specific movement direction is required. Using forward dynamic simulations, a pertinent study by Buneo et al. (1995) demonstrated that neural noise in the implementation of muscle activations may cause directional biases. This study however provides limited support to our alternative interpretation because the prediction was that the diagonal directions would be most non-preferred, which is inconsistent with the preferences to produce strokes in these directions observed in our studies with the use of the free-stroke drawing task. Thus, further research is necessary to establish whether directional biases may be a result of factors affecting movement execution. Noteworthy, the two alternative interpretations are not mutually exclusive, i.e., in addition to the tendency to select the directions that require minimal interference with INT, the emergent biases may be further strengthened during stroke production due to systematic underproduction of MUS magnitude at the subordinate joint.

In summary, this study revealed that directional biases are mirror symmetrical in the D and ND arm. Results offer two alternative interpretations. One interpretation suggests that the directional biases emerged from a tendency of the D arm to exploit INT for the simplification of control of intersegmental dynamics. The ND arm was not able to take advantage of INT in the preferred directions, which suggests that planning of movement direction is mediated for both arms from a common center that employs both inverse and forward dynamic transformations. The other interpretation is that movement directions are planned evenly and directional biases emerge during movement execution due to influence of intrinsic factors common for the two arms.