Estimating West Nile Virus Transmission Period in Pennsylvania Using an Optimized Degree-Day Model

Abstract

We provide calibrated degree-day models to predict potential West Nile virus (WNV) transmission periods in Pennsylvania. We begin by following the standard approach of treating the degree-days necessary for the virus to complete the extrinsic incubation period (EIP), and mosquito longevity as constants. This approach failed to adequately explain virus transmission periods based on mosquito surveillance data from 4 locations (Harrisburg, Philadelphia, Pittsburgh, and Williamsport) in Pennsylvania from 2002 to 2008. Allowing the EIP and adult longevity to vary across time and space improved model fit substantially. The calibrated models increase the ability to successfully predict the WNV transmission period in Pennsylvania to 70–80% compared to less than 30% in the uncalibrated model. Model validation showed the optimized models to be robust in 3 of the locations, although still showing errors for Philadelphia. These models and methods could provide useful tools to predict WNV transmission period from surveillance datasets, assess potential WNV risk, and make informed mosquito surveillance strategies.

Introduction

West Nile Virus (WNV) is a single-stranded RNA virus belonging to the family Flaviviridae. It is transmitted amongst primary bird hosts by Culex mosquitoes (Family Culicidae) such as Culex pipiens, Cx. restuans, and Cx. tarsalis (Campbell et al. 2002), with transmission via these vectors causing infections in secondary/dead-end hosts such as humans and horses. Following its arrival in New York City in 1999 (Lanciotti et al. 1999), WNV has spread across the continental United States (Peterson 2001, Nash et al. 2001, Sugumaran et al. 2009). Each year, between 60 and 9000 human infections are reported in the United States, with a total of >30,600 confirmed cases and 1200 fatalities to date (Centers for Disease Control and Prevention 2011). One of the key surveillance tools is routine monitoring of mosquito populations for infected mosquitoes during potential WNV transmission periods.

As with many vector-borne diseases, key life history traits of both vector and pathogen are affected by environmental temperature (Rueda et al. 1990, Dohm et al. 2006a, Bellan et al. 2010). In particular, the extrinsic incubation period (EIP) of the virus, which is the time it takes following an initial infected blood meal for the virus to replicate and disseminate within the mosquito and for the mosquito to become infectious, exhibits a strong temperature dependence (Reisen et al. 2006, Kilpatrick et al. 2008, Bolling et al. 2009). For example, at 18°C it takes around 30 days for Cx. tarsalis to be able transmit the virus, whereas at 30°C it takes less than 1 week (Reisen et al. 2006). This temperature dependence has been characterized using a degree-day model (Allen 1976) where the number of days required for 50% of mosquitoes to be able to transmit (EIP₅₀) takes 109 accumulated degree-days (109 DD) above a minimum development threshold of 14.3°C (Reisen et al. 2006).

When combined with a measure of adult mosquito longevity, the degree-day model of the EIP provides a potential tool to define the spatial and/or temporal limits for WNV transmission (Reisen et al. 2006). That is, if conditions are too cold to enable accumulation of sufficient degree-days within the average life span of a female mosquito, then the chances of transmission are low (note the reverse is not true as more factors are involved in transmission than simply exceeding the thermal threshold). Several studies have used this approach to explore WNV risk. For example, Zou et al. (2007) examined WNV occurrence in Wyoming between 2003 and 2005. Using the standard degree-day model and a 12-day average life span for Culex (Dohm et al. 2006b), they were able to predict temporal (±1 week) and spatial variation in the first week of potential WNV transmission in the year (measured as the first positive samples of infected mosquitoes collected from the field) with about 80% accuracy. Konrad et al. (2009) also used this approach to explore WNV transmission dynamics in Cx. tarsalis in Santa Barbara, California. In this case, however, model accuracy was rather poor until the degree-day accumulation for the EIP was adjusted to a much lower 76 DD.

Here, we investigate whether this type of degree-day modeling method can be used to characterize the transmission period of WNV in Pennsylvania, where Cx. pipiens and Cx. restuans, rather than Cx. tarsalis, are the dominant WNV vectors. Our study draws on an extensive mosquito surveillance data set collected between 2002 and 2008 across Pennsylvania by the Pennsylvania Department of Environmental Protection. These data provide a measure of the time and location of first and last positive mosquito samples collected across each year. We begin using the standard degree-day model (Zou et al. 2007) to explore the first and last detection dates (hence the potential transmission period is between these two dates) for WNV at 4 dispersed locations in Pennsylvania (Philadelphia, Harrisburg, Williamsport, and Pittsburgh) across 7 years (2002 to 2008). We then explore various adjustments in model parameters to optimize model performance. The major objective of this study was to evaluate the robustness of previous degree-day approaches (Zou et al. 2007, Konrad et al. 2009) and provide an optimized degree-day model to predict potential West Nile virus transmission period in different locations in Pennsylvania.

Materials and Methods

Background environmental and mosquito data

We selected 4 sites to cover a range of latitudes and longitudes across Pennsylvania: Harrisburg, Pittsburgh, Philadelphia, and Williamsport. Daily minimum and maximum temperature data for meteorological stations at these sites were obtained from National Oceanic and Atmospheric Administration (NOAA) (www.noaa.gov).

Mosquito surveillance data collected between 2002 and 2008 were provided by the Pennsylvania Department of Environmental Protection. Mosquito/WNV data for the current analysis were selected from sampling sites within 15 km of the 4 meteorological stations. The surveillance data include: Georeferenced trap location and type, number of mosquitoes collected, life stage of mosquito sampled (egg, larvae, pupae, adult) and their species habitat type, the number of mosquito pools (batches) tested, and quantity of mosquitoes in each pool (pool size). Mosquitoes were sorted by species and the presence of WNV for each pool was determined using RT-PCR. If the test result was positive, then the pool was considered to be WNV positive, regardless of pool size. Each pool consists of only 1 species. For the purpose of this study, we used data associated with the adult mosquitoes only.

Modeling WNV transmission using original degree-days model approach

We began with the basic model of Zou et al. (2007). This approach estimated potential for WNV transmission on each day of the transmission period by computing degree-day accumulation over a previous time frame as the vector mosquitoes' adult longevity. That is, in each day the accumulated degree-day is recorded by adding the net heat units above a base development threshold (for example, if the average temperature in the day is T_d then the net heat unit in that day is T_d − 14.3°C, given T_d>14.3°C; otherwise net heat unit is 0), plus the total net heat units in the previous 11 days, to represent the total heat units a mosquito could potentially accumulate during its 12-days adult longevity. The degree-day accumulation was then compared to the transmission threshold defined by the extrinsic incubation period (actually the EIP₅₀) of the virus to see whether WNV transmission could potentially occur that day. The first and last day for potential WNV transmission confine the WNV transmission period in a year. The EIP₅₀ was set at 109 DD with a minimum temperature threshold for development of 14.3°C (Reisen et al. 2006). Mosquito longevity was set at 12 days (Dohm et al. 2006b), and we did not consider vertical transmission because it is a relatively rare event (<0.1%; Dohm et al. 2006a). Other sources reported different extrinsic incubation (e.g., Richards et al. 2007), but for the initial test we followed the approach of Zou et al. (2007) and used the parameters reported under nonconstant temperatures by Reisen et al. (2002) and Dohm et al. (2006b).

We computed the degree-day accumulation for each day across the season (from calendar day 150 to calendar day 300) recording the first and last day in the season that the degree-day accumulation was above the EIP₅₀ threshold. Before day 150, the temperature is too low for the mosquitoes to accumulate any degree-days in Pennsylvania (i.e., daily mean temperature below 14.3°C, even in Philadelphia, the warmest location). So we suggest that using day 150 as a starting point is adequate to capture any potential WNV transmission. We then compared these predicted dates with observed dates based on the RT-PCR measures of the pooled mosquito samples (the first and last dates when WNV positive pools occur in a specific year and location), and computed the error (difference between the observed and predicted days) and used this error as the criterion to evaluate model performance. We considered a prediction to be ‘accurate’ if it was within±10 days of the observed data (this threshold was selected here as we felt 10 days was sufficient resolution to make informed operational decisions regarding surveillance and control).

To more precisely model degree-day accumulation we used daily maximum and minimum temperatures at each site to reconstruct the hourly temperature profile in a day, incorporating the influence of photoperiod (Parton and Logan 1981, Martinez 1991, Forsythe et al. 1995). The daily temperature profile is given by:

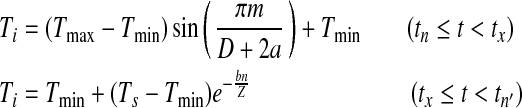where T_i is the hourly temperature, T_max and T_min are daily maximum and minimum temperature, respectively, D is day length (determined by latitude and day in a year), Z is night length, T_s is the temperature at the moment of sunset, m is number of hours after minimum temperature until sunset, n is number of hours after sunset until the time of minimum temperature of the next day, a is the lag coefficient for the maximum temperature, and b is the nighttime temperature coefficient (Parton and Logan 1981, Forsythe et al. 1995). A detailed description and derivation of the degree-day accumulation model is presented in Appendix A.

Improving model performance

As seen later, and consistent with the Californian study of Konrad et al. (2009), the original degree-day model parameters failed to capture the WNV transmission period in Pennsylvania adequately. There could be many reasons for this inconsistency (e.g., different life history parameters in the field compared with lab estimates, possibly different mosquito or virus strains, effects of acclimation or local adaption, etc.), and we have no robust data to adjust parameters empirically. Hence, we applied an optimization technique and explored a range of values for both mosquito longevity and EIP to identify the optimal combination that minimizes the error between predicted first and last WNV transmission dates and field observations. To do this, we divided the potential transmission period into 2 intervals—day 150 to day 210 (May 25 to July 29) representing the early period, and day 211 (July 30) onward representing the late period. The logic here is that we expect virus development and mosquito survival to be depend on local biotic and abiotic factors, and there is no reason to assume fixed parameters across the entire transmission period. For instance, Richards et al. (2007) reported variable EIP values. For each interval we explored a specific value of EIP and longevity, allowing the EIP to vary from 89 DD to 129 DD, with a 10 DD step, and longevity to vary from 10 to 14 days with 1-day step. This creates 625 different EIP×longevity parameter combinations. Each set of predictions (first and last day of transmission period) from these simulations was compared to the observed data. Optimal parameter combinations were identified by selecting the smallest total absolute error values between prediction and observation over all 7 years.

Model validation

Model validation was carried out by cross-validation. We split the data into 2 parts, picked 6 out of 7 years data (2002–2007) for modeling (with 2008 data for validation), applied the optimization process discussed above, and generated the new optimal parameter combinations. The new parameters (see Model validation section, below) were used to predict the transmission period in 2008 and evaluated against actual 2008 observations. If the new parameters are similar or identical to those derived from entire dataset, and the error between prediction and 2008 observation is small, then our model is accurate and robust. This validation process should ensure that our model is capable of predicting future transmission periods of WNV in Pennsylvania.

Results

Surveillance data

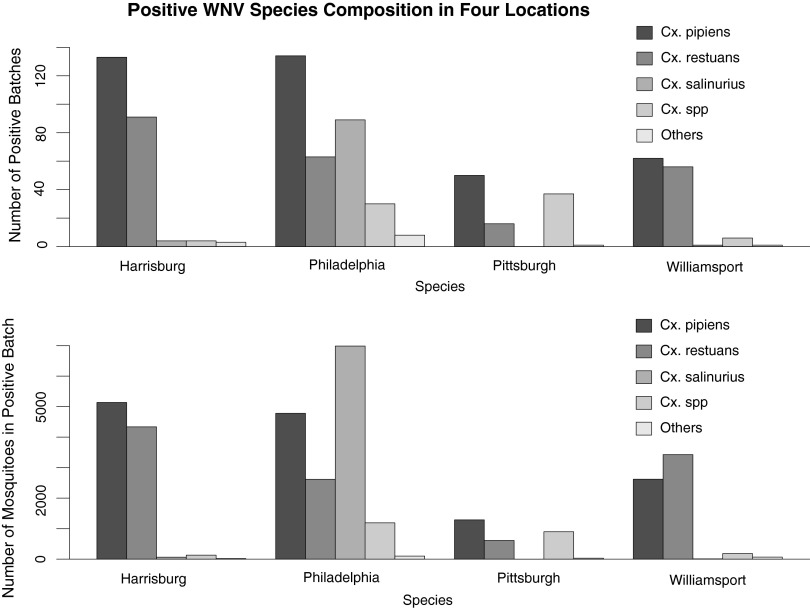
Across the various sites and years, a total of 790 pools were diagnosed as WNV positive, consisting of 34,720 mosquitoes in these pools. Pool size varied from 2 mosquitoes/pool to 120 mosquitoes/pool, with a mean pool size of 43 mosquitoes/pool. The number of positive pools for WNV was generally higher in Harrisburg and Philadelphia than Pittsburgh and Williamsport (Fig. 1), and the number of total pools tested does not vary substantially across the 4 locations. Cx. pipiens and Cx. restuans were the dominant vector species in Harrisburg, Pittsburgh, and Willamsport (i.e., these species comprised greater than 10% of the mosquitoes in WNV-positive pools; Fig 1). Cx. salinarius was an additional potential vector species in Philadelphia (Fig 1).

FIG. 1.

West Nile virus (WNV)-positive species composition in 4 locations from 2002 to 2008. (Upper panel) Number of positive pools, regardless of pool size. Cx. pipiens is the most abundant species in all locations, followed by Cx. restuans, except in Philadelphia. In Philadelphia, the second most abundant species is Cx. salinarius. (Lower panel) Number of total mosquitoes in positive pools. Cx. salinarius is the most abundant in Philadelphia, but not present in Pittsburgh at all, and has a low quantity in Harrisburg and Williamsport as well. This figure summarizes the species composition over entire 7-year period. We do not observe substantial species composition change among different years.

Original degree-days model results

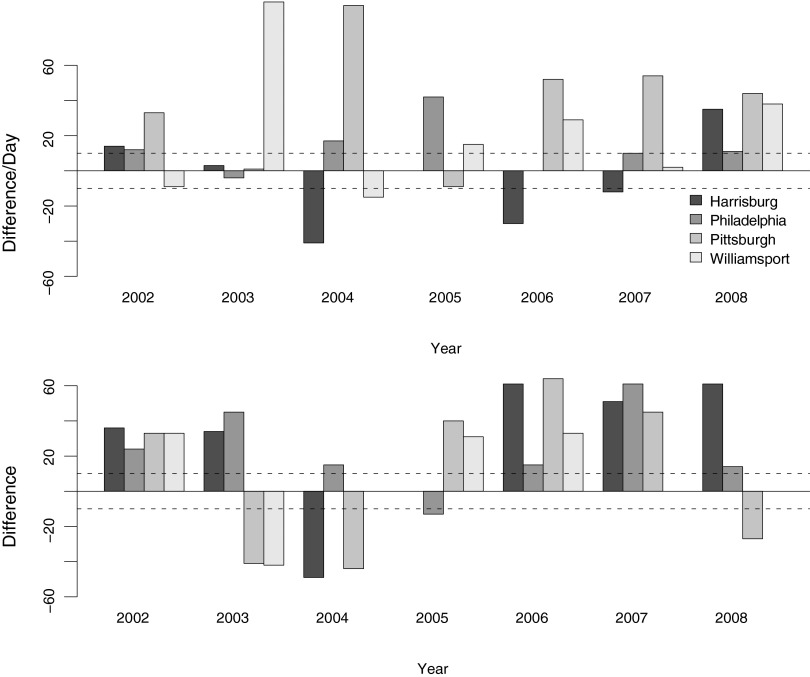
Comparing the first and last potential WNV transmission dates in each year based on the Zou et al. (2007) model (109 DD for EIP and 12 days for longevity) with field observations in all 4 locations generally overestimates the duration of the WNV transmission period (Table 1 and Fig. 2). Across sites and years, the model only predicts 7 of the first detection points within 10 days, with the remaining 15 predictions tending to predict earlier detection than observed, and 4 later than observed. Even worse, the model completely fails to predict the last potential transmission period within 10 days interval, with 18 earlier predictions and 6 later predictions (Table 1 and Fig. 2).

Table 1.

Predicted, Observed Detection Dates and Difference (in days) in Original Model

		Harrisburg		Philadelphia		Pittsburgh		Williamsport
Year	Location	First	Last	First	Last	First	Last	First	Last
2002	Predicted	3-Jul	28-Aug	28-Jun	14-Sep	15-Jul	22-Aug	5-Jul	24-Aug
	Observed	17-Jul	2-Oct	9-Jul	8-Oct	17-Aug	24-Sep	25-Jun	26-Sep
	Difference	14	36	12	24	33	33	−9	33
2003	Predicted	8-Jul	15-Aug	30-Jun	3-Sep	4-Aug	27-Oct	10-Apr	27-Oct
	Observed	11-Jul	18-Sep	26-Jun	17-Oct	5-Aug	16-Sep	15-Jul	15-Sep
	Difference	3	34	−4	45	1	−41	96	−42
2004	Predicted	13-Jul	27-Oct	22-Jun	6-Sep	10-Apr	27-Oct	25-Aug	25-Oct
	Observed	23-Aug	8-Sep	9-Jul	21-Sep	13-Jul	13-Sep	10-Aug	10-Aug
	Difference	−41	−49	17	15	94	−44	−15	NA*
2005	Predicted	15-Jun	17-Oct	13-Jun	26-Sep	20-Jul	20-Aug	6-Jul	14-Aug
	Observed	NA	NA	25-Jul	13-Sep	11-Jul	29-Sep	21-Jul	14-Sep
	Difference	NA	NA	42	−13	−9	40	15	31
2006	Predicted	21-Jul	10-Aug	7-Jun	29-Aug	12-Jun	8-Aug	3-Jul	10-Aug
	Observed	21-Jun	11-Oct	31-Aug	12-Sep	2-Aug	11-Oct	1-Aug	11-Sep
	Difference	−30	61	NA*	15	52	64	29	33
2007	Predicted	6-Aug	10-Aug	14-Jul	18-Aug	7-Jul	12-Aug	5-Aug	3-Oct
	Observed	25-Jul	4-Oct	24-Jul	18-Oct	30-Aug	26-Sep	7-Aug	NA
	Difference	−12	51	10	61	54	45	2	NA
2008	Predicted	18-Jun	23-Jul	13-Jun	11-Sep	16-Jun	27-Oct	20-Jun	25-Sep
	Observed	22-Jul	23-Sep	24-Jun	25-Sep	31-Jul	30-Sep	28-Jul	NA
	Difference	35	61	11	14	44	−27	38	NA

Note: Original model has a constant EIP₅₀ (109 DD) and a constant adult longevity (12 days). NAs indicate no record in the field data. NA^*s indicate unreliable calculation due to suspicious outlier observations (i.e., the observed date varies substantially from both predicted date and other years). First indicates first detection date of positive WNV incidence while Last indicates last detection date. We present predicted first and last detection dates for 2002–2008. The difference is calculated as subtracting observed date (converted to calendar day in a year) from predicted date for the first detections, and subtracting predicted date from observed date for the last detections.

EIP, extrinsic incubation perio; DD, degree-days.

FIG. 2.

Difference of observation and model prediction in original model. (Upper panel) First detection dates of potential West Nile virus (WNV) transmission. (Lower panel) Last detection dates. Two dashed lines:±10 days interval of success prediction. The last detection incidence dates are always poorly predicted in the original model.

Variable EIP and longevity adjustment

The dataset from the 625 parameter combinations is too large to show here and is available in Chen (2012). We found that recalibrating the Zou et al. (2007) model to include an EIP of 109 DD and mosquito longevity of 10 days at the beginning of the season (up to day 210), and then an EIP of 89 DD and longevity of 12 days thereafter, resulted in the smallest total prediction error over all 4 locations during the 7 year surveillance period.

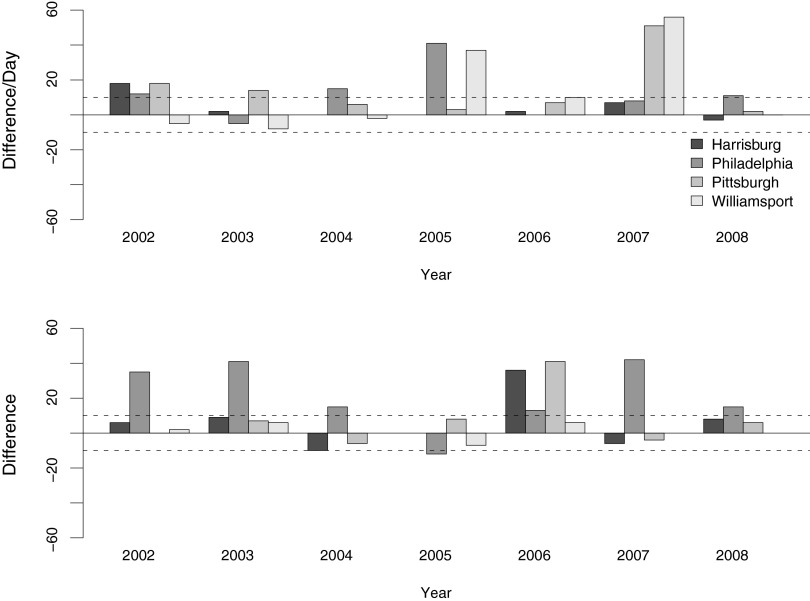
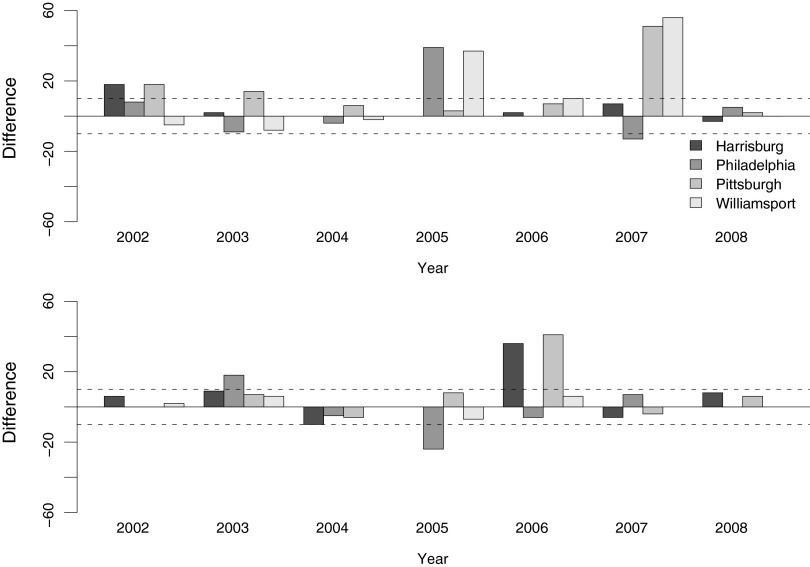
These parameter adjustments improved the model fit substantially (Table 2 and Fig. 3). For the 25 available first detection data points, the adjusted model predicts 15 of them within a 10-day window. The remaining 10 unsuccessful predictions are all earlier than observed. For the 24 last transmission dates, the adjusted model correctly reports 15 incidences. Of the 9 unsuccessful cases, 8 are earlier than observed, and 1 is later. Interestingly, nearly 80% of these errors (7 out of 9) in the adjusted model are associated with Philadelphia, suggesting that the model works well for the other sites but Philadelphia is in some way unusual. The reasons for the differences between sites are unclear but could include both biotic and abiotic factors. Philadelphia, for example, had a mean annual temperature approximately 3°C (significantly) higher than the other locations during the 2002–2008 period. In addition, the dominant species of infected mosquito late in the season in Philadelphia is Cx. salinarius, whereas this species is largely absent from the other sites. From a practical point of view, to improve model fit, we examined optimum longevity and EIP parameters for Philadelphia alone, regardless of the mechanisms. The parameter combinations that resulted in the lowest error were 159 DD for EIP and 10 days for adult longevity for early season, and 109 DD EIP and 12 days adult longevity for late season. These adjustments provided a substantial improvementin the model fit for Philadelphia (Table 3 and Fig. 4), predicting 17 out of 25 (i.e., 68%) first transmission dates and 20 out of 24 (i.e., 83%) last transmission dates within 10 days, with combined successful rate of 75% for both first and last potential transmission dates.

Table 2.

Predicted, Observed Detection Dates, and Difference in Adjusted Model

		Harrisburg		Philadelphia		Pittsburgh		Williamsport
Year	Location	First	Last	First	Last	First	Last	First	Last
2002	Predicted	29-Jun	26-Sep	27-Jun	7-Sep	30-Jul	24-Sep	30-Jun	24-Sep
	Observed	17-Jul	2-Oct	9-Jul	8-Oct	17-Aug	24-Sep	25-Jun	26-Sep
	Difference	18	6	12	35	18	0	−5	2
2003	Predicted	9-Jul	9-Sep	1-Jul	6-Sep	19-Aug	9-Sep	7-Jul	9-Sep
	Observed	11-Jul	18-Sep	26-Jun	17-Oct	5-Aug	16-Sep	15-Jul	15-Sep
	Difference	2	9	−5	41	14	7	−8	6
2004	Predicted	13-Jul	18-Sep	24-Jun	6-Sep	7-Jul	19-Sep	8-Aug	20-Sep
	Observed	23-Aug	8-Sep	9-Jul	21-Sep	13-Jul	13-Sep	10-Aug	10-Aug
	Difference	NA*	−10	15	15	6	−6	−2	NA*
2005	Predicted	15-Jun	28-Sep	14-Jun	25-Sep	8-Jul	21-Sep	14-Jun	21-Sep
	Observed	NA	NA	25-Jul	13-Sep	11-Jul	29-Sep	21-Jul	14-Sep
	Difference	NA	NA	41	−12	3	8	37	−7
2006	Predicted	19-Jun	5-Sep	23-Jun	30-Aug	9-Aug	31-Aug	11-Aug	5-Sep
	Observed	21-Jun	11-Oct	31-Aug	12-Sep	2-Aug	11-Oct	1-Aug	11-Sep
	Difference	2	36	NA*	13	7	41	10	6
2007	Predicted	18-Jul	10-Oct	16-Jul	6-Sep	9-Jul	30-Sep	12-Jun	9-Oct
	Observed	25-Jul	4-Oct	24-Jul	18-Oct	30-Aug	26-Sep	7-Aug	NA
	Difference	7	−6	8	42	51	−4	56	NA
2008	Predicted	25-Jul	15-Sep	13-Jun	10-Sep	29-Jul	24-Sep	28-Jul	17-Sep
	Observed	22-Jul	23-Sep	24-Jun	25-Sep	31-Jul	30-Sep	28-Jul	NA
	Difference	−3	8	11	15	2	6	0	NA

Note: Adjusted model has variable EIP₅₀ and longevity prior to day 210 (109 DD and 10 days) and thereafter (89 DD and 12 days). NA, NA^*, first, and last have the same meaning as in Table 1. The observed dates are the same as in Table 1.

EIP, extrinsic incubation period; DD, degree-days.

FIG. 3.

Difference of observation and model prediction in adjusted model. (Upper panel) First detection dates. (Lower panel) Last detection dates. Two dashed lines:±10 days interval of success prediction. Note substantial improve over the original model.

Table 3.

Predicted, Observed Detection Dates, and Difference for Philadelphia using Optimal Parameters

Year	2002	2003	2004	2005	2006	2007	2008
First Pred.	19-Jun	2-Jul	28-Jun	16-Jun	28-Jun	6-Aug	19-Jun
First Obs.	27-Jun	1-Jul	24-Jun	24-Jul	31-Aug	24-Jul	24-Jun
Difference	8	−1	−4	39	NA*	−13	5
Last Pred.	8-Oct	9-Oct	26-Sep	7-Oct	18-Sep	11-Oct	25-Sep
Last Obs.	8-Oct	17-Oct	21-Sep	13-Sep	12-Sep	18-Oct	25-Sep
Difference	0	8	−5	−24	−6	7	0

Note: These specific optimal parameters (EIP₅₀=159 DD and longevity=10 days before day 210, EIP₅₀=109 DD and longevity=12 days thereafter) are different from what were used previously (optimization for all locations). These parameters only apply to Philadelphia and do not yield optimal results (minimizing total absolute error) for other locations.

EIP, extrinsic incubation period; DD, degree-days; NA, unreliable data.

FIG. 4.

Difference of observation and model prediction in adjusted model with calibration for Philadelphia. (Upper panel) First detection dates. (Lower panel) Last detection dates. Two dashed lines:±10 days interval of success prediction.

Model validation

The results of model validation are shown in Table 4. For Harrisburg, Pittsburgh, and Williamsport, the model with the optimized parameters described above worked very well, with only 2 parameters estimated differently for 2008; mosquito longevity after day 210 optimized as 11 days in Williamsport, and EIP before day 210 optimized as 99 DD in Pittsburgh (though note the original parameters were within the 10-day accuracy target for Pittsburgh). Hence the model appears robust in these 3 locations. For Philadelphia, the model is less robust, with newly optimized parameters are more variable and have lower accuracy of the predictions.

Table 4.

Results of Model Validation

Location	EIP 1	Longevity 1	Error 1	EIP 2	Longevity 2	Error 2
Harrisburg	109	10	−3	89	12	8
Pittsburgh	99 (109)	10	−9 (2)	89	12	6
Williamsport	109	10	0	89	11 (12)	NA
Philadelphia	139 (159)	12 (10)	17 (5)	79 (89)	12	−12 (0)

Note: Model validation is performed by using the climate data between 2002 and 2007, and generating the optimal life history parameters (EIP 1 represents EIP₅₀ before day 210, EIP 2 represents EIP₅₀ after day 210, longevity 1 represents adult longevity before day 210, and longevity 2 represents adult longevity after day 210). After that we use the new life history parameters to predict the emergence dates in 2008. The errors represent relative error between model prediction (using current parameters) and 2008 observation. Error 1 and error 2 represent first and last emergence date error, respectively. The value with an asterisk mark (^*) indicates that it's different from the value reported in section 3.3 (which is the value in the parentheses). Note that the model is relatively robust for Harrisburg, Pittsburgh, and Williamsport, but not very robust for Philadelphia.

EIP, extrinsic incubation period.

Discussion

It is well established that the transmission dynamics of mosquito-borne diseases such as WNV can be influenced by environmental temperature. Most critically, because the rate of pathogen development within the mosquito varies with temperature and the duration of the incubation period tends to be similar to the average mosquito life span (Kilpatrick et al. 2008), temperature strongly affects the proportion of mosquitoes that live long enough to potentially transmit the disease. By taking this relationship into account, simple degree-day models of pathogen development coupled with estimates of mosquito longevity can potentially be used to explore disease risk (at least as determined by the minimum thermal requirements necessary to enable transmission) (Reisen et al. 2006, Zou et al. 2007, Konrad et al. 2009). Here we followed this approach to examine WNV transmission potential in Pennsylvania. Our final model provided reasonably accurate (±10 day) predictions of the beginning and end of the WNV transmission period across 3 locations over 7 years. Slight adjustment of the parameters appeared to enable us to extend the model with reasonable accuracy to a further site (Philadelphia). Examinations of an even larger parameter space with finer increments may yield a better fit, although such efforts may exceed the biological resolution (which is limited by sampling resolution) of these data.

To fit the model to the observed data, we optimized the number of degree-days required to complete the EIP, and the average adult mosquito longevity, across a range of parameter values. The best model fit resulted in selection of different paired parameter combinations for the beginning and end of the season. Although it is not unreasonable to expect baseline adult longevity or EIP to vary across the season or with location (see later discussion), we have no explicit biological justification for the parameter values selected, or for the transition in values mid season. As such, our model provides a phenomenological description of the link between environmental temperature and transmission potential. This approach contrasts with certain other studies that have developed more complex mechanistic models to explore WNV risk (e.g., Tachiiri et al. 2006, Gong et al. 2010). However, our aim is to explore the utility of this more generic approach in an attempt to balance model accuracy and simplicity, and to advance the potential of mining surveillance data for estimating transmission period. To this end, we believe the model provides a number of valuable insights.

For example, on the basis of the surveillance data, transmission can occur from mid-June through to mid-October, giving a potential transmission window of around 120 days. However, within any 1 season and/or location the actual transmission period can start as late as mid-July and finish as early as late August (Tables 1 and 2). As such, the model could help inform surveillance practices, refining sampling efforts from the current calendar-based approach (sampling generally starts in May and progresses through to October) to a degree-day approach that better reflects actual risk, optimizing allocation of monitoring and control resources. The utility of this approach in Philadelphia warrants further investigation.

From a more fundamental perspective, the model raises interesting questions regarding mosquito and pathogen biology. Based on simulation, we suggest mosquito longevity be 10 days at the beginning of the season (calendar day 150 to calendar day 210) and 12 days later on. However, in laboratory studies (Reisen et al. 2006, Tachiiri et al. 2006), adult Culex mosquitoes had better survival under cooler conditions (like the early season) and reduced longevity under warmer conditions (like the later part of the season). These potentially conflicting results highlight a need for more detailed knowledge of mosquito life history under field conditions.

Similarly, the model works best when we assume the degree-days necessary to complete the EIP vary across the season. EIP is generally considered an intrinsic property of the pathogen (or at least of a specific vector-pathogen combination; Davis 1932), so identifying possible variation in the temperature-dependence of EIP across the season is an interesting finding. How various aspects of host and vector condition might interact with temperature to determine EIP is again an important area for future study.

Beyond these biological factors, certain aspects of the surveillance data will also influence our results. For example, sampling effort varies across the season and across sites and detecting WNV-positive mosquitoes in the early part of the year when prevalence is expected to be low potentially adds a bias to the model. Similarly, control operations will alter mosquito abundance and WNV prevalence above and beyond any effects of environmental temperature. Further exploration of such factors could improve model fit and increase capacity of this simple modeling approach to predict potential WNV transmission period.

Appendix A. Degree-Day Modeling Procedure Incorporating Daily Temperature Range

Mean Temperature Model

This is the simplest model, which treats daily mean temperature as the arithmetic mean of daily maximum and minimum temperature:

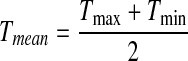The disadvantage of this model is obvious. Although T_mean is derived from daily maximum and minimum temperature, it does not contain any information about them, that is, we are ignoring DTR information completely.

Sine-negative exponential model

To overcome the problem inherited in the mean temperature model, biometerologists have proposed sine curve model (sinusoidal model) to simulate DTR profile, which has the basic form as:

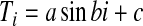Four inputs are required to reconstruct DTR profile: daily maximum temperature, minimum temperature to determine coefficient a and c. Coefficient b is determined by photoperiod, which itself is further considered as a function of latitude and number of the day in the year. Thus, we will need daily maximum, minimum temperature, latitude, and number of day in the year as inputs. The accumulated degree-day is basically the integration over basic development threshold. To reduce computational effort we interpolate hourly temperatures and use these temperatures to approximate degree-day accumulation above threshold in a day. This is a direct analog of Riemann Integral.

Forsythe et al. (1994) have proposed the following equations to calculate day length:

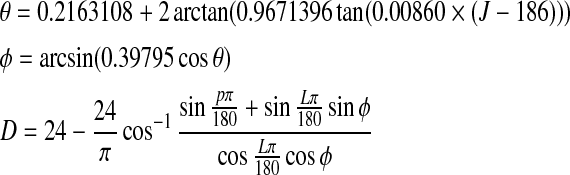where θ is the revolution angle predicted by number of day in the year (J), &phi; is the declination angle, L is latitude, and D is the day length. p is the sun position constant and equals 0.8333 according to US government definition (Forsythe et al. 1994).

While we have calculated the day length, we could further determine temperature profile in a day:

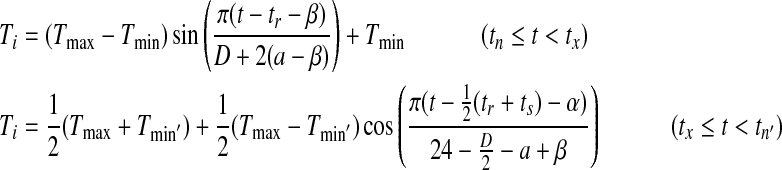where t is current time, D is day length, t_r and t_s are the sunrise and sunset time derived from day length, T_min’ is minimal temperature of the next day, and α and β are predetermined coefficients (Wann et al. 1985).

The sine-negative exponential model is a fine tuning version of the original sine curve model. Field observation data suggest that DTR is not necessarily symmetric in a day and the temperature curve after sunset is better fitted with a negative exponential curve. Thus, the final model is formulated as:

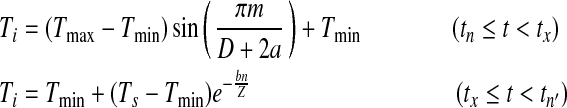where D is day length (determined by latitude and day in a year), Z is night length, T_s is the temperature at the moment of sunset, m is number of hours after minimum temperature until sunset, n is number of hours after sunset until the time of minimum temperature of the next day, a is the lag coefficient for the maximum temperature, and b is the nighttime temperature coefficient (Parton and Logan 1981). Because sine-negative exponential model is derived from sine curve model, we will call it sine curve model in the following text for simplicity.

Acknowledgments

We thank Dr. Mercedes Pascual, University of Michigan, for her helpful suggestions and discussion on some of the basic ideas of this manuscript.

This work was supported in part by the NSF-EID Program (grant no. EF-0914384).

Author Disclosure Statement

The other authors have no competing or conflicting financial interests to declare.