Modeling Time Varying Effects with Generalized and Unsynchronized Longitudinal Data

Summary

We propose novel estimation approaches for generalized varying coefficient models that are tailored for unsynchronized, irregular and infrequent longitudinal designs/data. Unsynchronized longitudinal data refers to the time-dependent response and covariate measurements for each individual measured at distinct time points. The proposed methods are motivated by data from the Comprehensive Dialysis Study (CDS). We model the potential age-varying association between infection-related hospitalization status and the inflammatory marker, C-reactive protein (CRP), within the first two years from initiation of dialysis. Traditional longitudinal modeling cannot directly be applied to unsynchronized data and no method exists to estimate time- or age-varying effects for generalized outcomes (e.g., binary or count data) to date. In addition, through the analysis of the CDS data and simulation studies, we show that preprocessing steps, such as binning, needed to synchronize data to apply traditional modeling can lead to significant loss of information in this context. In contrast, the proposed approaches discard no observation; they exploit the fact that although there is little information in a single subject trajectory due to irregularity and infrequency, the moments of the underlying processes can be accurately and efficiently recovered by pooling information from all subjects using functional data analysis. Subject-specific mean response trajectory predictions are derived and finite sample properties of the estimators are studied.

1 Introduction

The public health burden directly related to infection in the dialysis population is substantial. Current projections estimate the United States will have as many as 710,000 prevalent end-stage renal disease (ESRD) patients by the year 2015 [1]. Recently Dalrymple et al. [2] showed a significant burden of infection in patients on dialysis, finding that among patients aged 65 to 100 years, the rate of infection-related hospitalization was 52 and 53 per 100 person-years for patients on peritoneal and hemodialysis, respectively. The Comprehensive Dialysis Study (CDS) is a prospective cohort study of ESRD patients who newly initiated dialysis between September 2005 and June 2007 [3] where longitudinal serum samples were collected on a subset of participants within the first two years from the start of dialysis. In this work, we aim to examine the potential age-varying association between infection-related hospitalization status and serum C-reactive protein (CRP), a positive acute-phase protein marker of inflammation which is increased during inflammation.

Varying coefficient models ([4], [5]) are designed to capture complex age- (or more generally, time-) varying effects/associations in regression relationships. They have been widely used in longitudinal data analysis in the past decade due to their ability to capture time-varying associations, their ease in interpretation and natural graphical display of time-varying dynamics ([6]–[12]). Cai et al. [13] developed extensions to generalized varying coefficient models for modeling longitudinal generalized responses, such as binary variables (e.g., infection-related hospitalization status) or counts of events. The generalized varying coefficient model for longitudinal data is

$$E\{Y(t)\mid X(t)\}=g\{{\beta }_0(t)+{\beta }_1(t)X(t)\},$$ (1)

where g(·) is a known inverse link (transformation) function that relates the mean outcome to the longitudinal covariate X. Qu and Li [14] studied estimation in generalized varying coefficient models for longitudinal data using penalized spline expansions coupled with quadratic inference function approaches, while Zhang [15] used a generalized linear mixed model approach where a double penalized quasi-likelihood approach is used for estimation.

There are several major challenges in the estimation of the generalized varying coefficient models from the CDS data. First, the longitudinal measurements on the binary response, infection-related hospitalization status, and the continuous covariate, serum CRP concentration, are obtained at distinct time points (unsynchronized) within each subject. Hospitalization times are stochastic and do not coincide with serum CRP measurement times. In addition, longitudinal hospitalization data is naturally highly irregular and infrequent over time. Thus, longitudinal data characterized by a combination of unsynchronized, irregular and infrequent measurements pose substantial challenges to modeling time-varying effects. We note that in other longitudinal studies, these issues may arise due to missed and/or rescheduled visits, despite diligent plans to collect data contemporaneously and on regular follow-up schedules.

Existing methods for the regression modeling of longitudinal data cannot handle unsynchronized data. Binning has been proposed [16], as a data preprocessing step (if feasible), to synchronize the response and covariate measurements to make existing methods applicable. However, binning can lead to significant loss of data in irregular and infrequent longitudinal designs as will be shown in the simulation studies of Section 5. For the CDS data, binning leads to a loss of 69% of the repeated measurements (and 51% loss in subject sample size). Hence, in this work, we develop novel estimation procedures for generalized varying coefficient models based on unsynchronized, irregular and infrequent longitudinal data, obviating data loss due to preprocessing steps.

The proposed estimation procedures build on recent developments in the longitudinal data literature that introduce functional data analysis techniques ([17]–[21]) to address irregular and infrequent designs ([22]–[24]). Yao et al. ([25], [26]) used estimates of the covariance structure and mean function of the longitudinal trajectories for functional linear regression; Hall et al. [27] modeled a single generalized longitudinal response trajectory (without any covariates) using latent Gaussian processes based on functional data analysis. Recently, Senturk and Mueller [28], Senturk and Nguyen [29] and Kim et al. [30] developed the functional data analysis framework for estimation in the standard varying coefficient models and reported improved estimation results over standard estimation procedures such as local least squares in regression modeling of sparse continuous error-prone longitudinal data. However, there has been no work on modeling generalized longitudinal outcome, including binary and count data, in the framework of generalized varying coefficient modeling geared towards unsynchronized, irregular and infrequent designs.

The remainder of the paper is organized as follows. We detail the proposed estimation approaches in Section 2, where binning coupled with local maximum likelihood estimation is also outlined as a comparison/baseline approach in Section 2.4. Representations of the varying coefficient functions of interest via the moments of the underlying covariate and response processes are derived in Section 2.1 leading to our first direct approach to estimation of the varying coefficient functions. A second alternative approach based on reconstruction of the predictor processes at the observation time points for the response is outlined in Section 2.3. Both of the proposed approaches rest on ideas of borrowing strength from the entire data and dimension reduction. Hence, unlike binning, every observation contributes to the estimation of the varying coefficient functions and no observation is discarded. Furthermore, while standard approaches can predict the mean response only at the original sparse observation times, the proposed methods lead to subject-specific predictions of the mean response trajectories for the entire study period as outlined in Section 3. The proposed method is illustrated with the aforementioned CDS data in Section 4. Section 5 reports on simulation studies of the accuracy of the proposed estimation and prediction procedures, including comparisons with local maximum likelihood estimators coupled with binning. We conclude with a brief discussion in Section 6.

2 Estimation in Generalized Varying Coefficient Models

Consider the generalized response Y_i(t) and the longitudinal predictor X_i(t) for i = 1, …, n subjects in model (1). The observed covariate and response trajectories are assumed to be square integrable realizations of the random smooth processes X and Y. Unsynchronized, infrequent and irregular nature of the CDS data, as described in the previous section, is characterized by subject and variable specific random observation times and small total number of repeated measurements. To accommodate these data characteristics, we assume that the longitudinal response (Y_i) and the covariate (X_i) trajectories for subject i, are observed at distinct time points T_ij ∈ [0, T] and S_ik ∈ [0, T], for j = 1, …, N_i and k = 1, …, M_i, respectively. N_i and M_i denote the ith subject’s total number of repeated measurements for the response and covariate, respectively. We also assume additive measurement error on the longitudinal covariate, i.e., X_ik = X_i(S_ik) + ε_ik, where ε_ik are mean zero finite variance i.i.d. measurement errors. The repeated measurements on the generalized response are denoted by Y_ij = Y_i(T_ij).

2.1 Moments Representations of the Varying Coefficient Functions

In this section, we outline our first approach for estimation in generalized varying coefficient models based on the moments representations for the time-varying coefficient functions of interest. We consider an expansion of X_i about its mean function, where the variation about it’s mean is relatively small, i.e., X_i(t) = μ_X(t) + δZ_i(t), with μ_X(t) ≡ E{X(t)}, Z_i a mean zero, bounded variance stochastic process and δ > 0 an unknown small constant. Assuming that the function g is continuously differentiable, g′ does not vanish and inf_s∈D g′ (s) > 0 where D is the range of β₀(t) + β₁(t)μ_X(t), it holds by a Taylor’s expansion that

$$g\{{\beta }_0(t)+{\beta }_1(t)X(t)\}=g\{{\beta }_0(t)+{\beta }_1(t){\mu }_X(t)\}+\delta Z(t){\beta }_1(t)g^{\prime }\{{\beta }_0(t)+{\beta }_1(t){\mu }_X(t)\}+O_p({\delta }^2).$$

It follows that μ_Y (t) ≡ E{Y (t)} = g{β₀(t) + β₁(t)μ_X(t)} + O(δ²), since E{Z(t)} = 0 and

$$\begin{array}{l}{G}_{YX}(t,t)\equiv cov\{Y(t),X(t)\}=cov[g\{{\beta }_0(t)+{\beta }_1(t)X(t),X(t)\}]\\ ={\beta }_1(t)g^{\prime }\{{\beta }_0(t)+{\beta }_1(t){\mu }_X(t)\}cov\{X(t),X(t)\}+O({\delta }^3)\\ ={\beta }_1(t)g^{\prime }\{{\beta }_0(t)+{\beta }_1(t){\mu }_X(t)\}{G}_{XX}(t,t)+O({\delta }^3),\end{array}$$

where G_XX(t, t) ≡ cov{X(t), X(t)}. Hence, we obtain the following approximations to the time-varying coefficients of interest,

$${\beta }_1(t)\approx \frac{G_{YX}(t,t)}{g^{\prime }[g^{-1}\{{\mu }_Y(t)\}]G_{XX}(t,t)}\text{and}{\beta }_0(t)\approx g^{-1}\{{\mu }_Y(t)\}-{\beta }_1(t){\mu }_X(t).$$ (2)

The approximations in (2) imply plug-in estimators for the targeted varying coefficient functions β₁(t) and β₀(t), respectively; both up to terms of order O(δ²). Note that the derived expressions in (2) do not depend on δ; therefore, δ need not be estimated. Nevertheless, we study the sensitivity of the proposed estimators to different values of δ (i.e., different variance of X) via Monte Carlo simulations in Section 5.

Note that the derived expressions for the varying coefficient functions given in (2) depend only on population quantities. Hence, even though the data is unsynchronized and infrequent at the subject level, population moments can still be estimated effectively when the data from all subjects are pooled together as will be described in the next section.

2.2 Estimation of the Moments of the Underlying Stochastic Processes

The population moments are obtained through smoothing, which also allows for pooling of information from all subjects. In a first step, the mean functions of the longitudinal trajectories are obtained by smoothing the aggregated data (S_ik, X_ik) and (T_ij, Y_ij) for i = 1, …, n, k = 1, …, M_i and j = 1, …, N_i, with local linear fitting. This yields μ̂_X(t) and μ̂_Y(t), respectively. Next, we compute the raw covariances between (Y, X) and (X, X) as G_{Y X,i}(T_ij, S_ik) = {Y_ij − μ̂_Y (T_ij)}{X_ik − μ̂_X(S_ik)} and G_XX,i(S_ik, S_iℓ) = {X_ik − μ̂_X(S_ik)}{X_iℓ − μ̂_X(S_iℓ)}, respectively. To obtain the final smooth estimates of the covariances, Ĝ_{Y X} and Ĝ_XX, we feed the raw estimates, G_{Y X,i} and G_XX,i, into a two dimensional local least squares algorithm. Explicit expressions of the local least squares estimators are given in Senturk and Mueller [28]. For a computationally efficient bandwidth choice in the proposed one- and two-dimensional smoothing, we adopt the generalized cross-validation algorithm of Liu and Mueller [31].

To eliminate the effects of covariate measurement error on the auto-covariance Ĝ_XX, we exclude the diagonal raw covariance elements G_XX,i(S_ik, S_ik), i = 1, …, n, k = 1, …, M_i in the two-dimensional smoothing step. This is because the measurement error on the longitudinal predictor variables only affect the variance terms along the diagonal. More details on this phenomenon can be found in [25]–[26]. In order to guarantee the non-negative definiteness of the estimated auto-covariance matrix, we exclude the negative estimates of the eigenvalues and corresponding eigenfunctions from the functional principal component decomposition $G_{XX}(s,t)={\sum }_{\ell =1}^{\infty }{\rho }_{\ell }{\phi }_{\ell }(s){\phi }_{\ell }(t)$, where φ_ℓ denotes the eigenfunctions with non-increasing eigenvalues ρ_ℓ. Here, a nonparametric functional principal component analysis step would be employed on the smooth estimate of the auto-covariance surface by a standard discretization procedure to estimate the eigenfunctions and eigenvalues. Once these quantities are estimated, the final auto-covariance estimator is given as ${\widehat{G}}_{XX}(s,t)={\sum }_{\ell =1,{\widehat{\rho }}_{\ell }>0}^L{\widehat{\rho }}_{\ell }{\widehat{\phi }}_{\ell }(s){\widehat{\phi }}_{\ell }(t)$ where the total number L of eigen-components included can be chosen by various criteria, including the Akaike information criterion (AIC) or fraction of variance explained. (For more details, see Appendix A.3 of Senturk and Mueller [28].)

The estimated mean and covariance functions can be plugged into the varying coefficient function representations given in (2) to obtain

$${\widehat{\beta }}_1(t)=\frac{{\widehat{G}}_{YX}(t,t)}{g^{\prime }[g^{-1}\{{\widehat{\mu }}_Y(t)\}]{\widehat{G}}_{XX}(t,t)}\text{and}{\widehat{\beta }}_0(t)=g^{-1}\{{\widehat{\mu }}_Y(t)\}-{\widehat{\beta }}_1(t){\widehat{\mu }}_X(t).$$ (3)

We will refer to the above estimators as the moments estimators of the varying coefficient functions throughout the manuscript. Uniform consistency of the moments estimators, up to terms of order O(δ²) (see Section 2.1), follow from the uniform consistency of the moments estimators described above. More specifically, the uniform consistency of the proposed mean and covariance function estimates have been shown for continuous longitudinal observations in Yao et al. ([25], [26]) and generalized longitudinal observations in Hall et al. [27]. We study the sensitivity of the finite sample performance of the moments estimators to different δ values in the simulation studies of Section 5.

Note that instead of applying a binning procedure to each subject trajectory to synchronize the response and covariate measurements, the proposed method uses smoothing in the estimation of the population quantities. While regularization via smoothing of each subject’s trajectory may be appropriate for densely measured longitudinal data, the proposed approach with regularization applied at the estimation of the population moments is much more suitable for infrequent and unsynchronized designs. In this way, every observation on each subject, whether it be unsynchronized or infrequent, contributes to the estimation via the connection between the population moments and the varying coefficient functions given in (2).

For analysis with a fixed duration, when another time index is considered for the varying coefficient model, other than the duration of the study, such as age, we have subject-specific supports for the observed data: {a_i; X_i(S_ik); Y_i(T_ij)} for j = 1, …, N_i and k = 1, …, M_i, S_ik, T_ij ∈ [a_i + T₀, a_i + T₁] and T₀ < T₁. We will refer to this case as the fixed duration case throughout the manuscript. As we will describe in more details in the data analysis of Section 4, for the CDS data, the protein inflammation marker and hospitalization measurement times per subject are randomly scattered within the [100, 550] day interval of interest, after the initiation of dialysis. Hence, in this set-up, a_i refers to age at initiation of dialysis for subject i, T₀ = 100 and T₁ = 550. Since each subject is observed within 100 to 550 days from their baseline age (age at initiation of dialysis, marking the beginning of the study), the raw covariances are only available in a band around the diagonal of length twice the duration of the study (450 days). (This will be detailed in Section 4.) Hence, the smoothing needs to be performed only in this region around the diagonal. In addition, note that (2) involves only the diagonal values of the auto- and cross-covariance surfaces of the underlying covariate and response processes. Hence, the proposed age-varying coefficient models can be estimated based on an analysis with a fixed duration time, such as the analysis of the CDS data considered here. Properties of the proposed estimation procedures are studied in detail under both time indices, the duration of the study and subject age (similar to CDS data), in simulation studies of Section 5.

2.3 Reconstruction of the Predictor Processes and Local Maximum Likelihood Estimation

Since traditional estimation procedures for modeling longitudinal data can only handle synchronized data, our second proposed estimation approach uses the functional data analysis framework and the estimated population moments in Section 2.2 to reconstruct the predictor processes at the observation times of the response. Once the predictor measurements are obtained synchronized with the response for each subject, we utilize an extension of the local maximum likelihood estimators of Cai et al. [13] originally proposed for i.i.d. data to longitudinal data, to obtain estimators of the varying coefficient functions.

The starting point in reconstructing the predictor trajectories will be the Karhunen-Loéve expansion for the observed process for subject i,

$$X_{ik}={\mu }_X(S_{ik})+\sum _{\ell =1}^{\infty }{\xi }_{i\ell }{\phi }_{\ell }(S_{ik})+{\epsilon }_{ik},$$

where ξ_iℓ is the ℓth functional principal component score playing the role of random effects with E(ξ_ℓ) = 0 and var(ξ_ℓ) = ρ_ℓ, ε_ik is the zero-mean finite variance measurement error introduced before, S_ik ∈ [0, T] and k = 1, …, M_i. Estimation of the mean function μ_X(t) and the auto-covariance operator G_XX from noise contaminated infrequent and irregular observed data have been outlined in the previous section. The eigenfunctions φ_ℓ(t) can be recovered through a functional principal component step applied to the discretization of the smooth auto-covariance estimator Ĝ_XX. Following the works in [25]–[26], Senturk and Mueller [28] proposed to recover ξ_iℓ from infrequent observations on the longitudinal predictor using Gaussian assumptions on all eigen-scores and measurement error of the longitudinal predictor based on the conditional expectation E(ξ_iℓ|U_i, M_i, S_i). Here U_i is the M_i × 1 observation vector U_i ≡ (X_i1, …, X_iMi)^T with X_ik = X_i(S_ik) + ε_ik and M_i and S_i = (S_i1, …, S_iMi) are the total number of repeated measurements and the vector of observation time points for subject i, respectively. Readers are referred to [28] for explicit expressions of ξ̂_iℓ. Next, putting together all estimated model components, we reconstruct the predictor process at the observation time points of the response: ${\stackrel{\sim }{X}}_{ij}\equiv {\widehat{\mu }}_X(T_{ij})+{\sum }_{\ell =1}^L{\widehat{\xi }}_{i\ell }{\widehat{\phi }}_{\ell }(T_{ij})$, T_ij ∈ [0, T] and j = 1, …, N_i. Here, the number L of eigen-components included can be chosen by various criteria, including AIC and the fraction of variance explained.

For reconstruction in analysis with a fixed duration, such as our analysis of the CDS data, we estimate the eigenfunctions and eigenvalues of the covariate process via pooling all covariate observations on the common observation period [T₀, T₁]. For this, we use predictor trajectories shifted from subject-specific supports S_ik ∈ [a_i + T₀, a_i + T₁] to the common observation period S_ik − a_i ∈ [T₀, T₁], for example within the [100, 550] day interval after the initiation of dialysis for the CDS data. (Details are provided in the data analysis of Section 4.) Once the predictor processes are reconstructed at the response observation times T_ij − a_i ∈ [T₀, T₁] within the common observation period, they are then shifted back to subject-specific supports T_ij ∈ [a_i + T₀, a_i + T₁] by adding a_i. In summary, we reconstruct on subject-specific intervals where the subject was originally observed, without extrapolation.

Using the synchronized data (T_ij, X̃_ij, Y_ij) for j = 1, …, N_i, we utilize a local maximum likelihood procedure for estimation of the varying coefficient functions. Assuming β₀(t) and β₁(t) have continuous second derivatives, we approximate each function locally by β₀ ≈ a₀ + a₁(t − t₀) and β₁(t) ≈ b₀ + b₁(t − t₀) for t in a neighborhood of the fixed time point t₀. Local maximum likelihood estimators aim to maximize the local log-likelihood,

$${\ell }_n(\mathbf{a},\mathbf{b})=\frac{1}{{\sum }_{i=1}^n{N}_i}\sum _{i=1}^n\sum _{j=1}^{N_i}\ell \left(g\left[a_0+a_1(T_{ij}-t_0)+\{b_0+b_1(T_{ij}-t_0)\}{\stackrel{\sim }{X}}_{ij}\right],Y_{ij}\right)K_h(T_{ij}-t_0),$$ (4)

where K_h(·) = K(·/h)/h, K(·) denotes a kernel function, h is the bandwidth, a ≡ (a₀, a₁)^T, b ≡ b₀, b₁)^T and ℓ(·, ·) denotes the log-likelihood function. Maximizing the local log-likelihood ℓ_n(a, b) results in the local maximum likelihood estimators for the varying coefficient functions β̂₀(t₀) = â₀ and β̂₀(t₀) = b̂₀. These second set of estimators obtained for the varying coefficient functions will be referred to as reconstruction estimators throughout the manuscript. The maximization can be implemented using the Newton-Raphson algorithm, with the r + 1 iteration update given by

$${({\widehat{\mathbf{a}}}_{r+1},{\widehat{\mathbf{b}}}_{r+1})}^{\text{T}}={({\widehat{\mathbf{a}}}_r,{\widehat{\mathbf{b}}}_r)}^{\text{T}}-{\left\{{\ell }_n^{″}({\widehat{\mathbf{a}}}_r,{\widehat{\mathbf{b}}}_r)\right\}}^{-1}{\ell }_n^{\prime }({\widehat{\mathbf{a}}}_r,{\widehat{\mathbf{b}}}_r),$$ (5)

where ${\ell }_n^{\prime }(·,·)$ and ${\ell }_n^{″}(·,·)$ denote the gradient and Hessian matrix of the log-likelihood, respectively. Explicit forms of the terms involved in the updating step (5) is given for the Bernoulli and Poisson distributed responses in the Appendix.

Note that the proposed reconstruction for the predictor process is quite different from preprocessing steps such as binning or smoothing a single subject’s trajectory. While the latter use only information from that particular subject, the proposed approach uses the pooled information from all subjects. Functional data analysis framework provides a unique opportunity for synchronizing the response and predictor measurements using the estimated underlying population quantities, moments of the predictor process. Comparisons of the two proposed approaches based on functional data analysis, along with a binning coupled with local maximum likelihood approach, outlined below, are given in the simulation studies and data analysis.

2.4 Binning and Local Maximum Likelihood Estimation

In this section we outline an equidistant binning procedure to synchronize the data followed by local maximum likelihood for estimation of the varying coefficient functions, as a baseline method in comparisons with the proposed estimators. For the equidistant binning, the maximum number of equidistant bins per subject is selected such that each bin contains at least one repeated measurement on the covariate and the response. In applications, the maximum number of bins would be selected from a preliminary set of total number of bins that is determined by the distributions of the subject-specific total number of repetitions for the covariate and the response, M_i and N_i, respectively. More specifically, for subject i, the binning yields synchronized data (t_ib, X_ib, Y_ib) for b = 1, …, B_i bins, where the time t_ib denotes the midpoint of the bth bin, X_ib is the average of the covariate observations X_ik and Y_ib is the sum of the response observations Y_ij falling in bin b. We use the sum of the binary and count response values within a bin to yield Binomial and Poisson distributed response values, respectively, after binning.

The synchronized data obtained from binning is then fed into a local maximum likelihood procedure for estimation of the varying coefficient functions. For binned data (t_ib, X_ib, Y_ib) with possibly reduced total number of subjects i = 1, …, n_B (n_B ≤ n) and possibly reduced repetitions per subject b = 1, …, B_i (B_i ≤ min{N_i, M_i}), local maximum likelihood estimators aim to maximize the local log-likelihood,

$${\ell }_{n_B}(\mathbf{a},\mathbf{b})=\frac{1}{{\sum }_{i=1}^{n_B}{B}_i}\sum _{i=1}^{n_B}\sum _{b=1}^{B_i}\ell \left(g\left[a_0+a_1(t_{ib}-t_0)+\{b_0+b_1(t_{ib}-t_0)\}{X}_{ib}\right],Y_{ib}\right)K_h(t_{ib}-t_0),$$

where K_h(·) = K(·/h)/h, K(·) denotes a kernel function, h is the bandwidth, a ≡ (a₀, a₁)^T, b ≡ (b₀, b₁)^T and ℓ(·, ·) denotes the log-likelihood function. Maximizing the local log-likelihood ℓ_nB (a, b) with similar computations as in Section 2.3, we obtain what we will refer to as binning estimators for the varying coefficient functions β̂₀(t₀) = â₀ and β̂₀(t₀) = b̂₀.

3 Prediction of Subject-Specific Mean Response Trajectories

While the traditional estimation methods, such as the binning estimator outlined above, can only predict the mean response at the bin midpoints t_ib, we will utilize functional data analysis techniques to provide smooth predicted mean response trajectories throughout the duration of the study based on the two proposed estimation procedures. We begin by the Karhunen-Loéve expansion of the covariate trajectory of a new subject, $X^{\ast }(t)={\mu }_X(t)+{\sum }_{\ell =1}^{\infty }{\xi }_{\ell }^{\ast }{\phi }_{\ell }(t)$ where ${\xi }_{\ell }^{\ast }={\int }_0^T\{X^{\ast }(t)-{\mu }_X(t)\}{\phi }_{\ell }(t)dt$ is the ℓth functional principal component score with $E({\xi }_{\ell }^{\ast })=0$ and $var({\xi }_{\ell }^{\ast })={\rho }_{\ell }$. Based on the generalized varying coefficient model (1), the predicted response trajectories will be obtained through

$$E\{Y^{\ast }(t)\mid X^{\ast }(t)\}=g\{{\eta }^{\ast }(t)\}=g\left\{{\beta }_0(t)+{\beta }_1(t){\mu }_X(t)+{\beta }_1(t)\sum _{\ell =1}^{\infty }{\xi }_{\ell }^{\ast }{\phi }_{\ell }(t)\right\},$$ (6)

where η^*(t) ≡ β₀(t) + β₁(t)X^*(t) and Y^*(t) denotes the generalized response trajectory of a new subject.

The eigenfunctions φ_ℓ(t) and eigen-scores ${\xi }_{\ell }^{\ast }$ are estimated as outlined in Section 2.3 based on the conditional expectation $E({\xi }_{\ell }^{\ast }\mid U^{\ast },M^{\ast },S^{\ast })$, where U^* is the M^* × 1 observation vector $U^{\ast }\equiv {(X_1^{\ast },\dots ,X_{M^{\ast }}^{\ast })}^{\text{T}}$ with $X_k^{\ast }=X^{\ast }(S_k^{\ast })+{\epsilon }_j^{\ast }$ and M^* and $S^{\ast }=(S_1^{\ast },\dots ,S_{M^{\ast }}^{\ast })$ are the total number of repeated measurements and the vector of observation time points of the new subject, respectively. Thus, using this plug-in estimate for (6) enables us to predict individual mean response trajectories in the generalized varying coefficient model by

$${\widehat{Y}}_L^{\ast }(t)=g\{{\widehat{\eta }}^{\ast }(t)\}=g\left\{{\widehat{\beta }}_0(t)+{\widehat{\beta }}_1(t){\widehat{\mu }}_X(t)+{\widehat{\beta }}_1(t)\sum _{\ell =1}^L{\widehat{\xi }}_{\ell }^{\ast }{\widehat{\phi }}_{\ell }(t)\right\}.$$ (7)

Here β̂₀(t) and β̂₁(t) refer to the moments and reconstruction estimators of the varying coefficient functions proposed, leading to predictions from the two estimation proposals, respectively. Note that the resulting predictions are for t ∈ [0, T], i.e. the trajectory on the entire time domain, not just for the original infrequent observation times S^*.

For prediction in analysis with a fixed duration, such as our analysis of the CDS data, we begin by predicting subject-specific predictor trajectories on the interval [T₀, T₁] by using all predictor trajectories shifted from subject-specific supports [a_i + T₀, a_i + T₁] to the common observation period [T₀, T₁], similar the reconstruction procedure described in Section 2.3. The predicted subject-specific trajectories are then shifted back to subject-specific supports, for example to [a_i + T₀, a_i + T₁] for subject i. Hence even though the varying coefficient functions are estimated on [min(a_i) + T₀, max(a_i) + T₁], we only need the estimated functions from [a_i + T₀, a_i + T₁] to obtain our predicted response trajectories on [a_i + T₀, a_i + T₁] for subject i. In this way we don’t extrapolate in prediction of the fixed duration case; we predict on subject-specific time intervals where the subject was originally observed.

4 Application to Data from the Comprehensive Dialysis Study

4.1 Description of CDS Data and Analysis Cohort

Longitudinal CRP levels were available for a subset of 266 participants in the CDS study (with 1 to 5 measurements per subject) and their infection-related hospitalization data was obtained from the USRDS database. The median time to the first serum collection is about 6 months after the initiation of dialysis and then samples were taken approximately every three (median) months thereafter. The minimum time to first serum sample collection is about 3.4 months; therefore, CRP measurements are mostly between [100, 550] days from the initiation of the dialysis. To avoid boundary bias (due to extremely few data points at the boundaries) we consider longitudinal measurements on a subset of 228 patients with CRP measurements in this [100, 550] days period (approximately 1.2 years). This analysis cohort yields 729 total longitudinal CRP measurements (with 47, 35, 30, 58, 58 subjects with 1 to 5 measurements, respectively). The median baseline age is 63.6 (standard deviation 10.0). There are 304 total hospitalizations, of which 88 were infection related. The total number of hospitalizations per person range between 0 to 16. Because hospitalization events are stochastic, times of infection-related hospitalization statuses (0 or 1) and CRP measurement times are unsynchronized, in addition to being highly irregular and infrequent.

As mentioned earlier, a preliminary binning step to synchronize the data leads to 51% loss in the subject sample size since nearly half of the subjects are missing a response measurement. In terms of the total number of measurements, this represents about 69% data loss. In our analysis below, we compare the two proposed estimators, moments and reconstruction as well as binning estimators. We note that in the application of the binning, we search for the maximum number of bins formed for each subject such that each bin contains at least one covariate and response measurement, as outlined in Section 2.4. We search for the maximum bin number for each subject starting from 5 (and decreasing to 0), since the maximum total number of CRP measurements per subject and hence the maximum number of bins is 5. Nearly half of the subjects have zero bins, with no response measurements and subject-specific total number of bins range from 0 to 3. In contrast, individuals with CRP measurements but without any hospitalizations still contribute to the proposed estimation procedures and in particular are used to estimate the auto-covariance G_XX(t, t) in the proposed methods.

4.2 Data Analysis Results

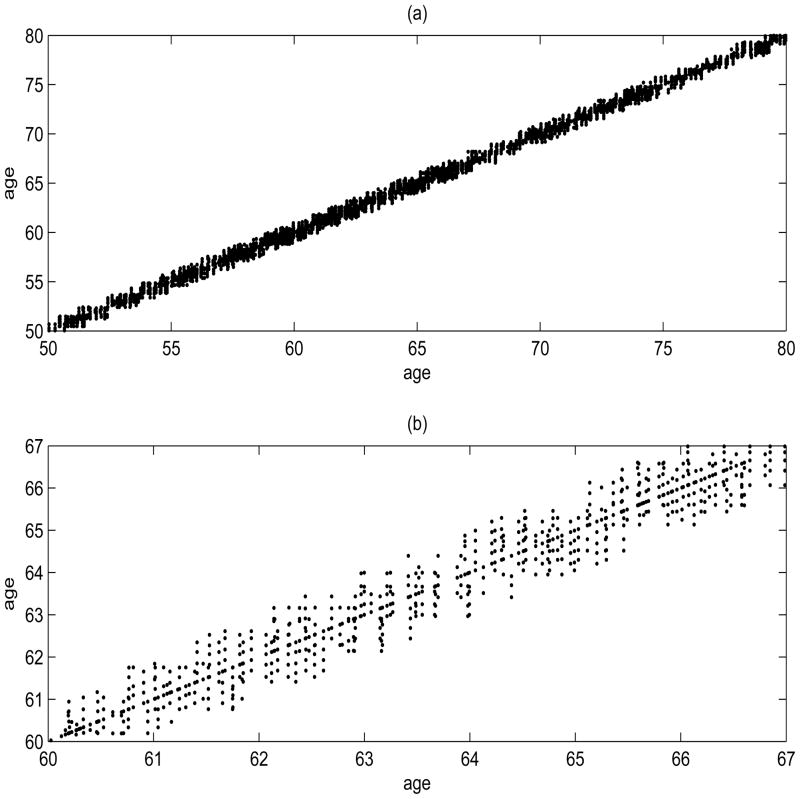
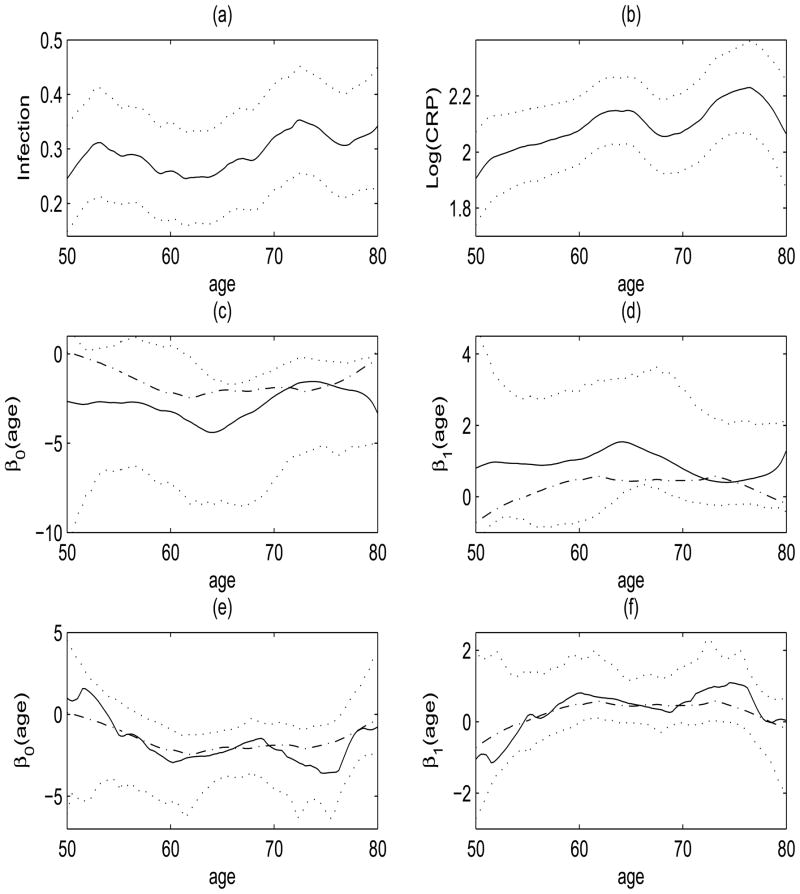
To illustrate the proposed methods, we consider estimation of the age-varying association between longitudinal infection-related hospitalization status and a protein inflammation marker, serum CRP levels. Since CRP has a skewed distribution, we take the logarithm transformation for our analysis. The auto-covariance support in age scale of log(CRP) is given in Figure 1, where both the auto- and cross-covariances are estimated within about a 1.2 year band ([100, 550] days from the initiation of dialysis) around the diagonal. The estimated cross-sectional mean functions for the response and the covariate are given in Figure 2(a)–(b), where the infection probability and mean log(CRP) concentration is increasing slightly with age.

Figure 1.

(a) Support (S_ik, S_iℓ), k, ℓ = 1, …, M_i, i = 1, …, n, of the auto-covariance for the covariate process. (b) A closer view of the support for ages between 60 and 67.

Figure 2.

(a)–(b) The smoothed cross-sectional estimate of the mean function μ̂_Y (age) (solid) for the presence of an infection-related hospitalization (a) and μ̂_X(age) (solid) of log(CRP) (b) along with ±2 sliding window standard deviation error bars (dotted). (c)–(d) Estimated varying coefficient functions β₀(age) (c) and β₁(age), the slope function of log(CRP) (d) from the proposed moments fits (solid) along with moments based 90% bootstrap confidence intervals (dotted) for the CDS data. Estimated functions from the binning fits (dash-dotted) are also displayed. (e)–(f) Estimated varying coefficient functions from proposed reconstruction fits (solid) and binning fits (dash-dotted) along with reconstruction based 90% bootstrap confidence intervals (dotted).

The estimated age-varying coefficient functions from the three estimators, moments, reconstruction and binning are also given in Figure 2. More specifically, the middle row ((c)–(d)) contains comparisons of the moments (solid) and binning (dash-dotted) fits along with moments based bootstrap confidence intervals (dotted), while the last row contains comparisons of the reconstruction (solid) and binning (dash-dotted) fits along with reconstruction based bootstrap confidence intervals (dotted). We utilize percentile point-wise confidence intervals based on 500 bootstrap samples obtained by resampling from subjects with repetition. Both moments and reconstruction approaches yield slightly more positive age-varying slope functions for the relationship between infection-related hospitalization status and log(CRP) over parts of age range 60 to 80 than the binning approach which hovers around zero over age. This observed positive association between infection-related hospitalization and inflammation markers, particularly CRP, is consistent with well-established findings in the literature on infection and CRP (see [32] and references therein). Although small sample sizes lead to wider bootstrap confidence intervals, as expected, the estimated slope functions based on the moments and reconstruction methods are found significant with the 90% confidence intervals, especially in the mid age range of (63–69) and (60–64, 72–74), respectively.

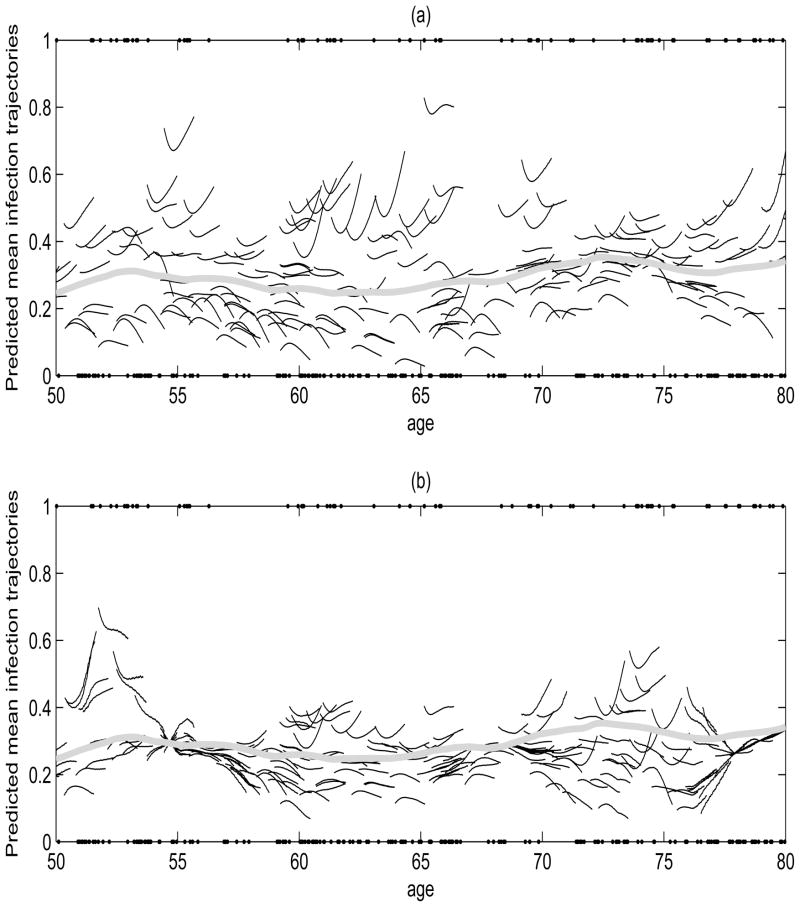
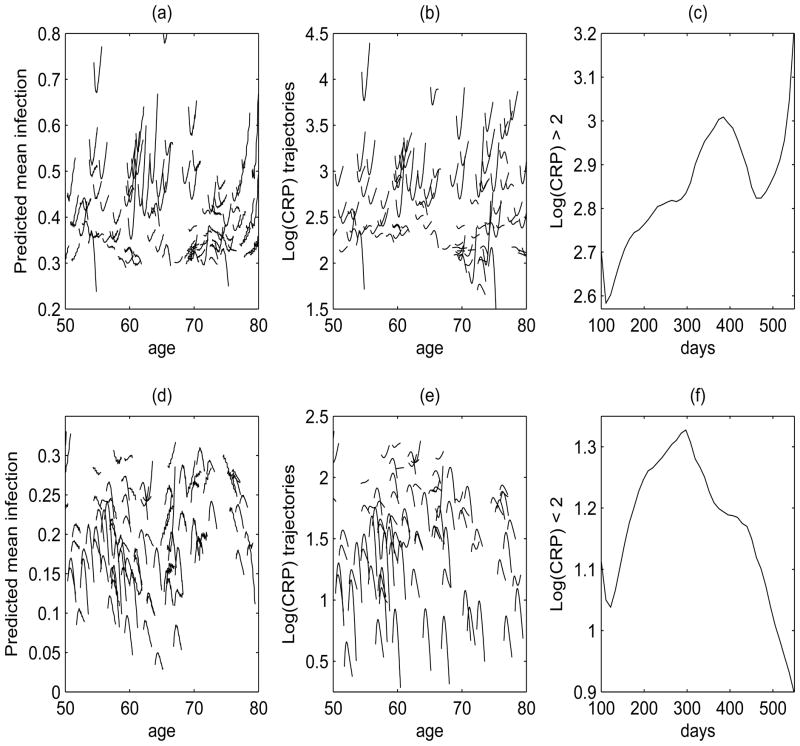
Next, we consider in more detail the predicted subject-specific mean response trajectories, corresponding to the predicted probability of having an infection-related hospitalization P{Y (t)} = 1, obtained for all subjects with the predicted subject’s data left out, provided based on moments and reconstruction estimates separately in Figure 3. Predictions based on the reconstruction estimates seem to vary less in general compared to predictions based on moments estimates, especially in regions around ages 55, 66 and 78, since these are the values where the reconstruction estimates of the slope function in Figure 3(f) cross zero. In addition, distinct concave and convex patterns in the 100 to 550 days from the initiation of dialysis are evident for subject-specific trajectories in both set of predictions, with estimated infection-related hospitalization probabilities roughly above (“high” risk) or below (“low” risk) the mean probability of infection of 0.3. Figure 4 displays the predicted response trajectories for these high and low risk groups based on moments estimators with their corresponding log(CRP) trajectories used in the predictions. The observed concave and convex age-varying subject-specific infection trajectories/patterns correspond to the subject-specific covariate log(CRP) trajectories (Figure 4(b) and (e)), explaining the patterns of the predicted mean response trajectories. That is, the high risk and low risk groups for infection-related hospitalization also correspond to patients with higher (mean CRP = 15.5) and lower (mean CRP = 5.0) CRP concentrations, roughly above and below log(CRP)= 2, respectively. We also plot the estimated mean trajectories of log(CRP) for these two groups, where a similar concave and convex pattern exist for the mean log(CRP) trajectories within 1.2 years from the initiation of dialysis (Figure 4(c) and (f)).

Figure 3.

(a)–(b) Observed values (dots) for presence of an infection-related hospitalization and predicted subject-specific mean response curves (solid) based on moments estimates (a) and reconstruction estimates (b). Also displayed (thick solid gray) is the smoothed estimate of the mean function μ̂_Y (age) of infection.

Figure 4.

(a) Predicted subject-specific infection-related hospitalization probability trajectories based on moments estimates for high infection risk group, and (d) for lower infection risk group. (b) Log(CRP) trajectories of the subjects with high infection probabilities corresponding to (a) and (e) similarly for subjects with lower infection-related hospitalization probability corresponding to (d). (c) Smoothed estimate μ̂_X of the mean log(CRP) trajectories for log(CRP) values higher than 2, and (f) lower than 2.

5 Simulation Studies

5.1 Simulation Design

We carry out three simulation studies to evaluate the performance of the proposed estimators for both binary and count responses. We study the properties of the proposed estimation procedures under three cases: (a) unsynchronized Bernoulli response, (b) unsynchronized Poisson response and (c) unsynchronized Bernoulli response with fixed study length resulting in a diagonal support for an age-varying coefficient model (analogous to the CDS analysis described above). Thus, cases (a) and (b) will allow us to more thoroughly assess the performance of the proposed methods generally, while case (c) is designed to mimic the characteristics of the CDS data. In all three scenarios, the proposed estimation algorithms, moments and reconstruction estimators are compared along with the baseline method of binning described in Section 2.4. The covariate process X is generated according to X_i(t) = μ_X(t) + ξ_i1φ₁(t) + ξ_i2φ₂(t), where the functional principal component scores ξ_i1 and ξ_i2 are simulated from independent normals with means zero and variances equal to σ². To study the sensitivity of the moments estimators to different δ values (see the Taylor’s expansions of Section 2.1), which correspond to different levels of variation in the covariate X, we report results for three different variances σ² of 2, 4, and 6. The predictor trajectories are assumed to be observed with measurement error which are simulated independently from a Gaussian distribution with zero mean and variance equal to 0.3. Reported results for all simulations are based on 200 Monte-Carlo runs. Technical details of the three data cases are given below.

Case (a)

The number of repeated measurements for n = 100 and 200 subjects are chosen randomly between 5 and 15 with equal probabilities, independently for the response (Y) and the covariate (X) to create unsynchronized design. The observation times T_ij and S_ik for each subject are randomly selected independently for the covariate and the response from the time interval [0, 10]. The mean function and two eigenfunctions for the predictor process are ${\mu }_X(t)=4sin(\pi t/5)/\sqrt{5},{\phi }_1(t)=-cos(\pi t/10)/\sqrt{5}$ and ${\phi }_2(t)=sin(\pi t/10)/\sqrt{5}$, 0 ≤ t ≤ 10, respectively. The varying coefficient functions are β₀(t) = sin(πt/5) and β₁(t) = −sin(πt/10). The response Y_ij are simulated from a Bernoulli distribution with mean E{Y_ij|X_i(T_ij)} = g{β₀(T_ij) + β₁(T_ij)X_i(T_ij)}, where g(p) = e^p/(1 + e^p).

Case (b)

For count response, the sample size, number of repetitions, observation times and the predictor process are generated in the same way as in case (a). The varying coefficient functions are β₀(t) = t/5 and β₁(t) = sin(πt/10)/3. The response Y_ij are simulated from a Poisson distribution with mean E{Y_ij|X_i(T_ij)} = g{β₀(T_ij)+ β₁(T_ij)X_i(T_ij)}, where g(p) = e^p.

Case (c)

To simulate data similar to the analyzed CDS data in Section 4, the number of repeated measurements for the response are chosen between 0 to 7 with probabilities [0.5, 0.15, 0.1, 0.1, 0.05, 0.05, 0.025, 0.025] and between 1 to 5 for the covariate with probabilities [0.15, 0.15, 0.20, 0.25, 0.25] for n = 200 and 400 subjects. The baseline age a_i of each subject is chosen randomly from [50, 79] where the repeated measurement times for that subject are then chosen randomly from the time interval [a_i, a_i + 1.2], separately for the response and the covariate processes. This leads to unsynchronized data, corresponding to a fixed (average) follow-up time of approximately 1.2 years, similar to diagonal support of the age-varying coefficient model for the CDS data. The mean function and the two eigenfunctions for the covariate process are ${\mu }_X(t)=sin\{\pi (t-50)/30\}\sqrt{15},{\phi }_1(t)=-cos\{(t-50)/30\}/\sqrt{15}$ and ${\phi }_2(t)=sin\{\pi (t-50)/30\}/\sqrt{15},50\le t\le 80$, 50 ≤ t ≤ 80, respectively. The age-varying coefficient functions are β₀(t) = −1.5 sin{π(t−50)/30} and β₁(t) = −2sin{π(t−65)/30}. The response Y_ij are simulated from a Bernoulli distribution with mean E{Y_ij|X_i(T_ij)} = g{β₀(T_ij) + β₁(T_ij)X_i(T_ij)}, where g(p) = e^p/(1 + e^p).

To study the performance of the proposed estimation method for the varying coefficient functions, we use relative mean squared deviation error (ME):

$${\text{ME}}_0=\frac{\int {\{{\beta }_0(t)-{\widehat{\beta }}_0(t)\}}^{2}dt}{\int {\beta }_0^2(t)dt}\text{and}{\text{ME}}_1=\frac{\int {\{{\beta }_1(t)-{\widehat{\beta }}_1(t)\}}^{2}dt}{\int {\beta }_1^2(t)dt}.$$

Overall ME will be the average of ME₀ and ME₁. For comparisons, the ME values are also obtained for the three estimation procedures, moments (ME_M), reconstruction (ME_R) and binning (ME_B) in the three simulation cases. In the implementation of the equidistant binning algorithm, for cases (a) and (b) we divide the study period [0, 10] into equidistant bins, and for case (c) we divide the subject-specific observation interval [min_k,j{S_ik, T_ij}, max_k,j{S_ik, T_ij}] into equidistant bins to synchronize the data prior to local maximum likelihood estimation.

In addition, we use relative mean squared prediction error (PE_i) to study the proposed subject-specific mean response trajectories, where

$${\text{PE}}_i=\frac{\int {[g\{{\eta }_i(t)\}-g\{{\widehat{\eta }}_i(t)\}]}^{2}dt}{\int g^2\{{\eta }_i(t)\}dt},$$

with η_i(t) = β₀(t) + β₁(t)X_i(t) and ${\widehat{\eta }}_i(t)={\widehat{\beta }}_0+{\widehat{\beta }}_1{\widehat{\mu }}_X(t)+{\widehat{\beta }}_1{\sum }_{\ell =1}^L{\widehat{\xi }}_{i\ell }{\widehat{\phi }}_{\ell }(t)$ based on moments estimates (PE_M) and reconstruction estimates (PE_R). To examine how the estimated population moments affect the overall quality of the varying coefficient function moments estimators given in (3), we define the following similar relative deviation quantities:

$$\begin{array}{l}{\text{ME}}_{YX}=\frac{\int {\{G_{YX}(t,t)-{\widehat{G}}_{YX}(t,t)\}}^{2}dt}{\int G_{YX}^2(t,t)dt},{\text{ME}}_{XX}=\frac{\int {\{G_{XX}(t,t)-{\widehat{G}}_{XX}(t,t)\}}^{2}dt}{\int G_{XX}^2(t,t)dt},\\ {\text{ME}}_{{\mu }_Y}=\frac{\int [g^{-1}\{{\mu }_Y(t)\}-g^{-1}\{{\widehat{\mu }}_Y(t)\}]dt}{\int {[g^{-1}\{{\mu }_Y(t)\}]}^{2}dt}\text{and}{\text{ME}}_{{\mu }_X}=\frac{\int {\{{\mu }_X(t)-{\widehat{\mu }}_X(t)\}}^{2}dt}{\int {\mu }_X^2(t)dt}.\end{array}$$

5.2 Simulation Results

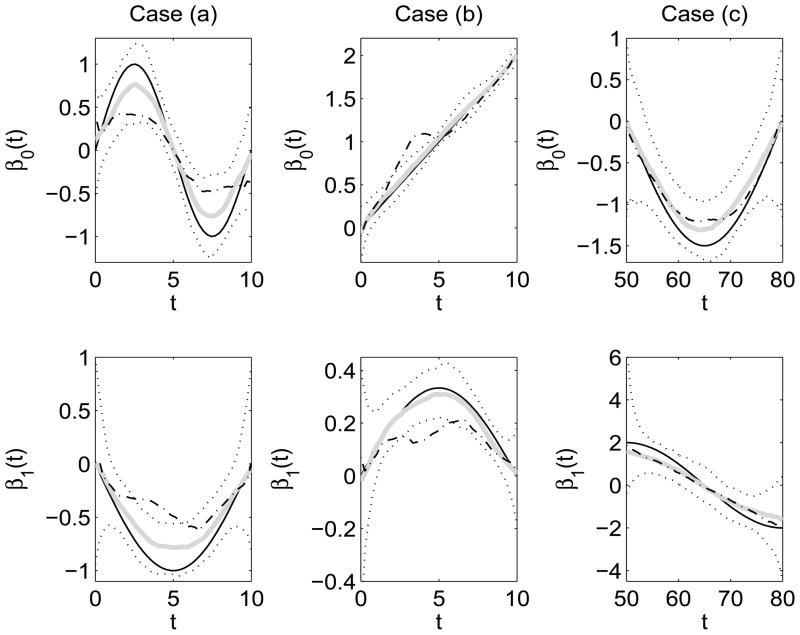
The cross-sectional medians and the 5% and 95% cross-sectional percentiles of the estimated varying coefficient functions from moments and binning methods are given in Figure 5 for the simulation cases (a), (b) and (c) with σ² = 4. (Percentiles of the reconstruction estimates which are close to the percentiles of the moments estimates are omitted in this plot.) For the proposed methods, the median varying coefficient estimates track the true coefficient functions more closely for all three cases. The (median) binning estimates deviate substantially more from the true underlying functions relative to the proposed estimates, especially in simulation cases (a) and (b) (see Figure 5). Results are similar for other simulation studies with varying σ² (not shown).

Figure 5.

Simulation results on estimated varying coefficient functions β₀(t) and β₁(t) for the three simulation set-ups: case (a) unsynchronized binary response, case (b) unsynchronized count response and case (c) unsynchronized binary response with diagonal support analogous to the CDS data. Displayed results are from simulations with σ² = 4. The cross-sectional median curves of the proposed moments estimates (thick solid grey) along with 5% and 95% cross-sectional percentiles (dotted) are plotted along with the true varying coefficient functions (solid). Also displayed are the cross-sectional median curves from binning fits (dash-dotted). Percentiles presented are based on 200 Monte Carlo runs/data sets.

The performance of the methods are summarized in more details in Tables 1 and 2, with respect to the relative mean squared deviation error (ME) and subject-specific relative mean squared prediction error (PE). More specifically, provided in Tables 1 and 2 are the median, 25% and 75% percentiles of ME and PE for the proposed moments and reconstruction estimators over all three simulation cases. Also reported for comparison is the ratio of the ME’s for the proposed methods over the binning approach, denoted by r_{ME, MB} and r_{ME, RB} for the moments and reconstruction methods, respectively. The ratios r_ME reported in Table 1 are roughly fluctuating around 0.1 to 0.2 for general unsynchronized data cases (a) and (b) and around 0.5 to 0.75 for unsynchronized data with diagonal support analogous to the CDS data (i.e., case (c)). Thus, the efficiency gain of the proposed methods over bining is about 80% to 90% for general unsynchronized data cases and about 25% to 50% for special case (c) with age-varying coefficient model under fixed study length analysis similar to the analysis of CDS data. The relative mean squared prediction error (see PE in Table 2) of the proposed prediction methods are quite small for all three simulation cases, showing clearly the efficacy of the proposed subject-specific predictions.

Table 1.

Relative mean squared deviation error based on moments (ME_M) and reconstruction (ME_R) estimates, ratios of two ME’s {moments (r_{ME, MB}) and reconstruction (r_{ME, RB}) estimates over binning estimates} for the three simulation set-ups: case (a) general unsynchronized binary response, case (b) general unsynchronized count response and case (c) unsynchronized binary response with diagonal support analogous to the CDS data. Median and 25% and 75% percentiles of the deviation measures are presented based 200 Monte Carlo runs/data sets.

Case	n	σ2	MEM			MER			rME, MB			rME, RB
			Med	25%	75%	Med	25%	75%	Med	25%	75%	Med	25%	75%
(a)	100	2	.182	.134	.254	.167	.114	.234	.197	.112	.344	.179	.106	.322
(a)	100	4	.136	.097	.196	.101	.069	.146	.212	.137	.329	.153	.090	.252
(a)	100	6	.115	.086	.159	.081	.060	.110	.222	.147	.319	.148	.088	.224
(a)	200	2	.114	.080	.154	.084	.056	.119	.183	.124	.252	.138	.088	.196
(a)	200	4	.083	.062	.118	.053	.035	.070	.200	.153	.280	.118	.080	.183
(a)	200	6	.087	.064	.117	.042	.032	.059	.231	.162	.325	.109	.073	.158
(b)	100	2	.084	.048	.124	.061	.039	.089	.223	.134	.398	.162	.090	.276
(b)	100	4	.040	.027	.066	.028	.018	.040	.156	.107	.321	.112	.067	.183
(b)	100	6	.034	.022	.049	.021	.013	.031	.178	.105	.290	.116	.065	.174
(b)	200	2	.040	.024	.065	.026	.016	.042	.158	.095	.256	.093	.059	.172
(b)	200	4	.024	.017	.038	.015	.009	.022	.135	.096	.217	.080	.049	.137
(b)	200	6	.019	.013	.026	.010	.007	.014	.134	.095	.194	.068	.045	.109
(c)	200	2	.217	.133	.315	.184	.121	.282	.679	.417	1.073	.589	.340	.886
(c)	200	4	.160	.119	.226	.128	.087	.198	.693	.395	1.214	.539	.345	.888
(c)	200	6	.158	.114	.218	.108	.072	.165	.657	.438	1.216	.487	.306	.797
(c)	400	2	.134	.087	.180	.101	.074	.142	.681	.450	1.051	.543	.380	.863
(c)	400	4	.102	.072	.134	.076	.055	.097	.804	.564	1.070	.636	.418	.896
(c)	400	6	.101	.070	.129	.059	.044	.088	.913	.648	1.265	.565	.378	.826

Table 2.

Relative mean squared prediction error based on moments (PE_M) and reconstruction (PE_R) estimates for the three simulation set-ups: case (a) general unsynchronized binary response, case (b) general unsynchronized count response and case (c) unsynchronized binary response with diagonal support analogous to the CDS data. Percentiles of the deviation measures presented are estimated from 200 Monte Carlo runs/data sets.

Case	n	σ2	PEM			PER
			Med	25%	75%	Med	25%	75%
(a)	100	2	.013	.008	.021	.012	.008	.019
(a)	100	4	.013	.008	.022	.012	.007	.019
(a)	100	6	.015	.009	.025	.012	.007	.020
(a)	200	2	.008	.005	.013	.007	.004	.011
(a)	200	4	.009	.006	.015	.007	.004	.011
(a)	200	6	.010	.006	.017	.007	.004	.011
(b)	100	2	.005	.003	.008	.004	.003	.007
(b)	100	4	.005	.003	.009	.004	.002	.006
(b)	100	6	.007	.004	.011	.004	.002	.006
(b)	200	2	.003	.002	.005	.002	.001	.004
(b)	200	4	.004	.002	.006	.002	.002	.004
(b)	200	6	.005	.003	.007	.002	.001	.004
(c)	200	2	.043	.012	.129	.054	.014	.156
(c)	200	4	.050	.013	.161	.055	.015	.160
(c)	200	6	.058	.015	.202	.051	.014	.161
(c)	400	2	.033	.008	.100	.045	.012	.132
(c)	400	4	.042	.011	.137	.047	.013	.138
(c)	400	6	.046	.012	.161	.042	.011	.124

There are several clear conclusions that can be drawn. First, there are gains over the binning combined with local-likelihood approach in all three cases (a, b and c) consistently with sample size. Second, the gains of the proposed approaches over binning is more in cases (a) and (b), where the time domain is common to all subjects. And this is expected since synchronizing the data through binning is expected to lead to more loss of information in the respective time index in cases (a) and (b). In cases (a) and (b), the time index for the varying coefficient model considered is the duration of the study and the predictor and response measurements span the entire observation interval leading to significant loss of information for synchronization methods such as binning. In contrast, in case (c), the time index of the varying coefficient model considered is age and the predictor and response measurements are only observed on subject-specific subsets of the entire age-domain, which leads to loss of less information in the age time-scale when data is synchronized via binning.

As for the comparison between the two proposed methods, moments and reconstruction approaches, we note that the reconstruction method leads to more favorable results over the moments estimators in estimation of the varying coefficient functions and prediction for simulation cases (a) and (b); moments estimators lead to smaller relative prediction error for simulation case (c), σ² = 2 and 4. Nevertheless, the moments approach provides a more direct approach to estimation without need for data synchronization, leading to computational savings compared to reconstruction approach, especially in simulation case (c). For example in simulation case (c), while the moments approach estimates the mean and covariance processes of the observed data only along the diagonal, the reconstruction approach additionally reconstructs each predictor trajectory based on the functional principle components decomposition of the shifted predictor trajectories. We note here that most of the computations involved in the proposed estimation algorithms (estimation of the moments of the predictor and response processes including the bivariate smoothing procedures and the choice of appropriate bandwidths and eigen-components, as well as reconstruction of the predictor trajectories) can be carried out with the publicly available software package PACE (http://anson.ucdavis.edu/~ntyang/PACE; [25], [26], [20], [21]).

Since the small δ assumption needed in the derivation of the moments estimators cannot be checked in applications, we study the sensitivity of the moments varying coefficient function estimators and predicted response trajectories to the constant δ, regulating the variance of the covariate process. Summaries of the error measures in Table 1 have been given for three different variation levels of X, namely σ² = 2, 4 and 6. More detailed summaries of the deviation of the separate components of the varying coefficient functions proposed in (3), specifically ME_{Y X}, ME_XX, ME_μY, and ME_μX are given in Table 3 for case (a). (The results are similar, for the other cases.) Since smaller σ² values correspond to a larger proportion of the variation in the observed covariate trajectories due to measurement error, the covariance processes and hence the varying coefficient functions become more difficult to estimate. The same phenomena has been reported by Hall et al. [27] in estimating eigenfunctions of the covariance processes. Hence, even though smaller σ², hence δ, values correspond to smaller biases from the Taylor expansion approximations, we observe an increase in the overall ME values as σ² decreases. However, relative mean squared prediction error is shown to be quite robust to the variation in the variance of the covariate. We conclude that the exact value of σ² (or equivalently δ) has a modest effect on the errors in estimation of the varying coefficient functions for both proposed methods (moments and reconstruction), while the individual predictions are relatively robust to fluctuations in σ².

Table 3.

Sensitivity of the proposed moments estimators to varying degrees of variation in the covariate process, σ², under simulation case (a) for general unsynchronized binary response. Relative mean squared deviation error is reported for both varying coefficient functions β₀ (ME₀) and β₁ (ME₁), along with deviation measures for the components of the varying coefficient function estimators, as defined in Section 5.1. Percentiles of the deviation measures presented are estimated from 200 Monte Carlo runs/data sets.

Case	n	σ2	ME0			ME1			MEY X	MEXX	MEμY	MEμX
			Med	25%	75%	Med	25%	75%	Med	Med	Med	Med
(a)	100	2	.191	.133	.282	.150	.101	.224	.166	.046	.321	.011
(a)	100	4	.156	.112	.222	.107	.074	.154	.115	.043	.406	.015
(a)	100	6	.158	.102	.234	.095	.064	.142	.092	.044	.393	.015

6 Discussion

The works reported here fill an important methodological gap. For unsynchronized longitudinal data where the time-dependent response and covariate measurements within each individual are measured at distinct time points, no estimation method exists to estimate time-varying effects in a generalized regression relationship. Informal approaches, based on preprocessing steps that use information in single subject trajectories to synchronize the data to make standard estimation methods applicable, as demonstrated in this work, lead to severe loss of data and introduce further estimation bias in irregular and infrequent longitudinal designs. The proposed methods based on functional data analysis framework resolve these challenges, by offering new ways for pooling information from all subjects under challenging longitudinal data structures, characterized by unsynchronized, irregular and infrequent longitudinal measurements.

The proposed methodology was motivated by an age-varying generalized regression model between unsynchronized longitudinal infection-related hospitalization status and serum CRP, a marker of inflammation, in the Comprehensive Dialysis Study. Alternative modeling of the CDS data has been suggested by one referee, where the index of the varying coefficient model can be set to time since dialysis (vintage) and baseline age can be included in the model as a cross-sectional covariate. Note that such a model with additional cross-sectional covariates can be readily implemented using the reconstruction estimation approach. The regression relationship as a function of vintage is also generally of interest in dialysis; however, it cannot be feasibly addressed with the current data, since follow time from initiation of dialysis is short. In addition, in this particular application, our scientific interest is the age-varying trends between CRP concentration and infection-related hospitalizations. We finally note that the proposed model with the age index carries different interpretations than the one where the index is time since initiation of dialysis.

As mentioned above, the reconstruction method can readily accommodate additional cross-sectional covariates, while including additional longitudinal covariates in the model would require further study for both proposed estimation techniques. Developments needed to accommodate additional longitudinal covariates would involve considering separate Taylor’s expansions for the additional covariates in the moments approach and would require joint reconstruction of multiple longitudinal predictor trajectories for the reconstruction method. We recognize these as topics that require further research.

It is also of interest to study the asymptotic distributions of the proposed estimators leading to asymptotic inference for the varying coefficient functions of interest. In addition, confidence intervals can be obtained for subject-specific mean response trajectories g{η^*(t)} given in (6), building onto the proposed confidence intervals of Senturk and Nguyen [29] for η^*(t) (the mean response trajectory in a varying coefficient model with continuous response). Senturk and Nguyen propose asymptotic pointwise confidence intervals for η^*(t) of the form ${\widehat{\eta }}^{\ast }(t)\pm \mathrm{\Phi }(1-\alpha /2)\sqrt{{\widehat{w}}_t}$, where Φ(·) denotes the Gaussian cdf and ŵ_t denotes the estimated asymptotic variance which is given in [29]. Multiple extensions can be considered for generalized varying coefficient models. A naive approach would be to consider the transformed confidence bounds $[g\{{\widehat{\eta }}^{\ast }(t)-\mathrm{\Phi }(1-\alpha /2)\sqrt{{\widehat{w}}_t}\},g\{{\widehat{\eta }}^{\ast }(t)+\mathrm{\Phi }(1-\alpha /2)\sqrt{{\widehat{w}}_t}\}]$ where η̂^*(t) is as given in (7). Another approach is to consider the confidence interval $g\{{\widehat{\eta }}^{\ast }(t)\}\pm \mathrm{\Phi }(1-\alpha /2)g^{\prime }\{{\widehat{\eta }}^{\ast }(t)\}\sqrt{{\widehat{w}}_t}$, where g′{η̂^*(t)} is used to target g′{η^*(t)}. However both proposals require further research to assess their properties.

Appendix

Newton-Raphson Updates for Local Maximum Likelihood Estimators

The log-likelihood function ℓ(p_ij, Y_ij) in (4) is equal to y_ij log(p_ij) + (1 − y_ij) log(1 − p_ij) and −p_ij + y_ij log(p_ij) − log(y_ij) for the Bernoulli and Poisson distributions, respectively, where p_ij = g[a₀ + a₁(T_ij − t₀) + {b₀ + b₁(T_ij − t₀)}X̃_ij]. In addition, for both Bernoulli and Poisson distributions, the Newton-Raphson update given in (5) will have the form

$${({\widehat{\mathbf{a}}}_{r+1},{\widehat{\mathbf{b}}}_{r+1})}^{\text{T}}={({\widehat{\mathbf{a}}}_r,{\widehat{\mathbf{b}}}_r)}^{\text{T}}+{\left\{\sum _{i=1}^n{\chi }_i^{\text{T}}{W}_{1i}({\widehat{\mathbf{a}}}_r,{\widehat{\mathbf{b}}}_r){\chi }_i\right\}}^{-1}\sum _{i=1}^n{\chi }_i^{\text{T}}{W}_{2i}{\stackrel{\sim }{Y}}_i({\widehat{\mathbf{a}}}_r,{\widehat{\mathbf{b}}}_r),$$

where ≡ {1, …, 1; X̃_i1, …, X̃_iNi; (T_i1− t₀), …, (T_iNi− t₀); (T_i1− t₀)X̃_i1, …, (T_iNi − t₀)X̃_iNi}^T is the predictor matrix of size N_i × 4, p̂_ij ≡ g[â_r0 + â_r1(T_ij − t₀) + {b̂_r0 + b̂_r1(T_ij − t₀)}X̃_ij], W_2i ≡ diag{K_h(T_i1 − t₀), …, K_h(T_iNi − t₀)} and Ỹ_i(â_r, b̂_r) ≡ (Y_i1 − p̂_i1, …, Y_iNi − p̂_iNi)^T. For the Bernoulli distribution, W_1i(â_r, b̂_r) ≡ diag{K_h(T_i1 − t₀) p̂_i1(1 − p̂_i1), …, K_h(T_iNi − t₀) p̂_iNi (1 − p̂_iNi)}, while for Poisson W_1i(â_r, b̂_r) ≡ diag{K_h(T_i1 − t₀)p̂_i1, …, K_h(T_iNi − t₀)p̂_iNi}.