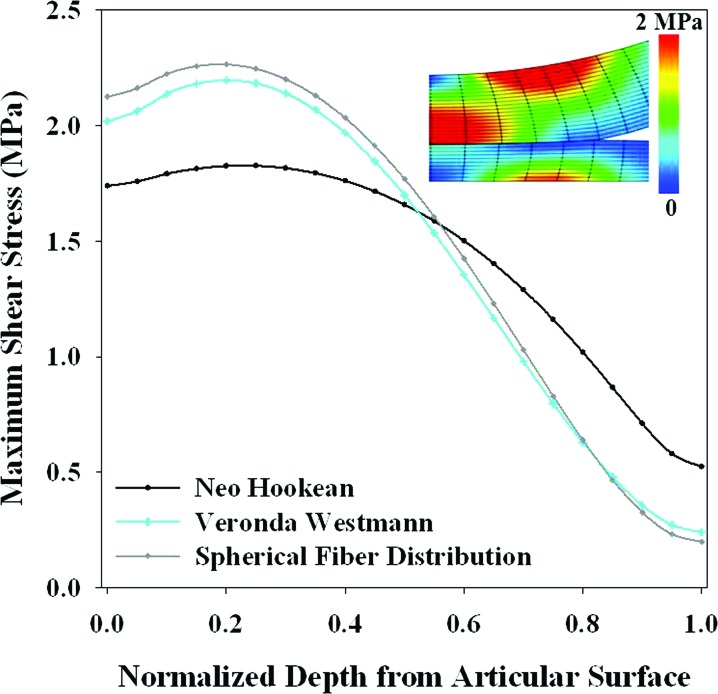
Fig. 9.

Maximum shear stress through the thickness as a function of nearly incompressible hyperelastic constitutive model for a plane strain analysis of a cylinder (outer radius of 20 mm, thickness of 2 mm) contacting a plate (thickness of 1 mm). The fringe plot shows results for the spherical fiber distribution model, because minimal differences were visible in the fringe plot between constitutive models. Shear stress was evaluated in the cylindrical layer at the location of peak contact stress (left border of fringe plot). The neo-Hookean constitutive model has both a lower maximum value at the contacting surface and a smaller change in maximum shear stress through the thickness of the layer. The Veronda Westmann and spherical fiber distribution constitutive models both captured larger maximum shear stress below the contacting surface than on the contacting surface. The differences between the neo-Hookean constitutive model and the other two combined with the similarity between the Veronda Westmann and spherical fiber distribution models suggests that material nonlinearity, not fiber reinforcement, is a salient feature for capturing maximum shear stress gradients through the thickness with this simplified geometry.