Degeneracy-Driven Self-Structuring Dynamics in Selective Repertoires

Abstract

Numerous biological interactions, such as interactions between T cell receptors or antibodies with antigens, interactions between enzymes and substrates, or interactions between predators and prey are often not strictly specific. In such less specific, or “sloppy,” systems, referred to here as degenerate systems, a given unit of a diverse resource (antigens, enzymatic substrates, prey) is at risk of being recognized and consumed by multiple consumers (lymphocytes, enzymes, predators). In this study, we model generalized degenerate consumer-resource systems of Lotka–Volterra and Verhulst types. In the degenerate systems of Lotka–Volterra, there is a continuum of types of consumer and resource based on variation of a single trait (characteristic, or preference). The consumers experience competition for a continuum of resource types. This non-local interaction system is modeled with partial differential-integral equations and shows spontaneous self-structuring of the consumer population that depends on the degree of interaction degeneracy between resource and consumer, but does not mirror the distribution of resource. We also show that the classical Verhulst (i.e. logistic) single population model can be generalized to a degenerate model, which shows qualitative behavior similar to that in the degenerate Lotka–Volterra model. These results provide better insight into the dynamics of selective systems in biology, suggesting that adaptation of degenerate repertoires is not a simple “mirroring” of the environment by the “fittest” elements of population.

1. Introduction

Despite the extreme complexity of biological systems, the commonly practiced reductionist approach often simplifies biological interactions to being “specific,” implying that the interacting entities do not engage in similar interactions with other, similar, entities. For example, an enzyme recognizes and converts a specific substrate but not an irrelevant substrate; a predator recognizes and consumes a specific kind of prey but not other types of prey; etc. An alternative, more realistic, approach is to consider most interactions as not being strictly specific. Indeed, enzymes, antibodies, and cellular receptors can bind not only their preferred substrates, antigens, or ligands, respectively, but also other resembling molecules. Similarly, a predator in most cases is capable of recognizing and consuming more than one kind of prey. As a result, realistic biological systems are composed of often structurally similar yet somewhat structurally differing elements, capable of performing similar yet somewhat differing but overlapping functions. Thus, a transition has to be made from considering simple specific interactions to considering repertoires of imperfectly interacting molecules, cells, or species.

Edelman (Edelman and Mountcastle, 1978; Edelman and Gally, 2001) was probably the first to introduce such a generalized view to selective systems, in which the elements of repertoires are selected by the signals from the environment. Edelman presented the immune system, nervous system, and ecological systems as broad repertoires of structurally different elements that function to some extent similarly. The elements in such repertoires have some degree of functional “limited sloppiness” (Fischer and Lipson, 1988), or, using Edelman's terminology (Edelman and Mountcastle, 1978; Edelman and Gally, 2001), “degeneracy,” which is different from redundancy. In redundant repertoires, the elements can be structurally similar or different, but perform similar functions. In degenerate repertoires, the elements form a continuum of structural variations resulting in similar, yet diverse, functions. Edelman and others later extended this view to numerous biological systems and pointed out that such limited functional sloppiness in biology is not a simple imperfection, but in many cases an important feature with far reaching biological consequences (see Edelman and Gally, 2001; Atamas et al., 1998; Atamas 1996, 2003, 2005 and references cited there for review). The degenerate repertoires have unique features that do not occur in any other known systems, such as adaptability to unpredictable future, exceptional reliability, and “associative memory” (Jerne, 1967; Ohno, 1978; Edelman and Mountcastle, 1978; Edelman and Gally, 2001).

A major consequence of degeneracy in selective degenerate biological repertoires is that more than one element will respond to an incoming signal. Therefore, a single influence from the environment will initially select not only a single unique “specific” element but also a population of degenerately responding, possibly less specific, elements. In other words, degeneracy of interaction of a selective repertoire with the environment will inevitably lead to competition, not only between exactly similar but also between similar yet diverse elements of the repertoire.

In this work we formulate degenerate resource–consumer model systems, in which a single kind of consumer responds to more than one kind of resource, and a single kind of resource can be recognized by more than one kind of consumer. Common sense prompts and modeling confirms that the non-specific nature of resource consumption will lead to intrinsic competition in such systems, resulting in dynamic self-structuring of a generalized “sloppy” repertoire (Atamas et al., 1998; Atamas 1996, 2003, 2005). Here we further develop this line of reasoning by considering degenerate versions of the classical Lotka–Volterra system and the Verhulst population model. In the next section we formulate degenerate forms of the Lotka–Volterra model (dLV) and the single-population Verhulst model (dV). In Section 3 we give some preliminary analysis of the dLV model, and present some results from numerically simulating the dLV model and dV models. In particular, we concentrate on behavior of the model near boundaries of the prey (resource) populations. In Section 4 we discuss implications of incorporating degeneracy mechanisms in diverse biological systems. The results suggest that the population of degenerate consumers undergoes spontaneous self-structuring into a distribution that does not mirror the distribution of resource. The degree of degeneracy affects the competition and leads to separation into subpopulations.

2. The models

Our goal is the formulation and analysis of a model incorporating sloppiness, or degeneracy, in a simple resource–consumer system, with implication going beyond ecology, to degenerate repertoires in general (Edelman and Mountcastle, 1978; Edelman and Gally, 2001; Fischer and Lipson, 1988; Atamas et al., 1998; Atamas 1996, 2003, 2005). Two well accepted population models, Lotka–Volterra and Verhulst (logistic growth) model, are expanded by incorporating degenerate consumption of resource by consumer.

Consider a space Z of characteristics, or traits, or food preferences, in which both consumer/predator and resource/prey are distributed. For purposes of simplification and clarity of discussion we will just consider Z to be one-dimensional, i.e. dynamics based on a single characteristic, though this is not essential to the ideas that are developed. The Z can denote any of various characteristics of resource “recognized” by the consumer. The modeled distributions in this generalized degenerate model need not, but may, be reflective of geometric distributions. In other words, Z may represent non-geometric characteristics. It could represent the continuum of antigens (resource) and, correspondingly, antibodies or T cell receptors (consumer), or the variety of cytokines (resource) and of responding cells (consumer). Alternatively, Z may represent geometric space. This could include the distributions of vegetation (resource) and herbivores (consumer) with increasing altitude level on a mountain. In the case of predator–prey dynamical interaction, the variety of a single trait for the prey is represented by Z, whereas for the consumer (predator), z ∈ Z is interpreted as a preference for that trait. In the analysis and numerical simulation, we will represent Z as the real numbers ℜ. In other circumstances it could be a simple real interval I, or the one-sphere S¹. For simulations we use a sufficiently long interval where simulations are run long enough to stabilize patterns but not to the point when the observed behavior is affected by the boundary conditions. For analysis purposes we assume that $Z=\Re$ unless stated otherwise.

Derivation of the degenerate Lotka–Volterra model (dLV)

Consider that both consumer y and resource x are distributed in the space Z of characteristics, or traits, or food preferences as described above. To remain consistent with the classical non-degenerate model, the term “predator” will be used for consumer and “prey” will be used for resource. In this distributed model, x(t, z) represents the density of resource and y(t, z) represents the density or biomass of the consumer at time t at location (or with characteristic) z. For a specific embodiment of the model, consider that space Z represents geometric space, with z being the altitude above the ground level. Then, plant foliage x(z) (resource, prey) in distributed in density over the ground—short, medium and tall grasses; short, medium and tall bushes; and short, medium and tall trees. Correspondingly, herbivorous animals y(z) are distributed on the same scale, from small rodents to giraffes. Such distributions are not limited to being merely spatial. For example, we can plot a distribution of speed z at which prey x(z) (e.g. smaller mammals) escape when chased by predators y(z) (larger carnivorous animals). In a similar fashion, antigens x(z) and antigen-recognizing B or T cells y(z) can be similarly distributed on a more abstract axis Z of “antigenic specificities.”

Due to the degenerate nature of resource consumption, not only x(t, z) but also x(t, z′) will be consumed by y(t, z); the closer z′ is to z, the more x(t, z′) is at risk of being consumed by y(t, z). Thus, due to the degenerate nature of resource consumption, different consumers (located at different z′) start competing for the same resource, and, reciprocally, resources located at different z′ will be consumed by the same unit of consumer. In this degenerate case, the demand for resource at z′ by a member of population at z depends on |z – z′| and is described by a kernel function k(|z – z′|), a unimodal function that characterizes, in a non-dimensional way, the degree of y(t, z) preference for resource at z′. We assume k(z) to be non-negative, piecewise continuous, and even (so the absolute value notation is dropped), and integrable. Without loss of generality we assume the kernels being normalized; that is, ∫_Z k(z)dz = 1. (For specific examples of the kind of kernels we employ in the analysis and simulation sections, see the Appendix A.) Hence, the resource/prey dynamics takes the form

$$\begin{array}{cc}\hfill \frac{\partial x}{\partial t}(t,z)& =\text{net growth}-\text{predation}\hfill \\ \hfill & =\text{net growth}-bx(t,z)\int k(z-z^{\prime })y(t,z^{\prime })d{z}^{\prime }.\hfill \end{array}$$

To simplify notation, the integration here and below is taken over Z unless otherwise expressed explicitly. While the prey populations are a resource for the consumer/predator populations in our model, there is an implicit need for a resource needed to maintain the population of prey itself. We will assume that the resources that sustain and allow growth of the prey population are supplied from an infinite reservoir and are replenished at the rate they are consumed. This resource assumption is implicit in all models and is just a convenience, both here and in the development of the dV model below, because these populations are in a hierarchy of a more general ecosystem, and we need to “close” the model system. But we do expect internal competition for these resources. This leads to a carrying capacity K, which, for purposes here of analytical tractability, is assumed to be independent of characteristic z. Similarly, the net (Malthusian) growth rate, a, a positive constant, represents the proliferative capacity per unit of population, and this is augmented by a c term representing the resource limits to the prey population in the spirit of Verhulst. Because of the z dependence, we use the term “per unit of population” instead of “per capita.” Thus, the prey populations have a z-independent carrying capacity K = a/c. We could include a degeneracy mechanism within the prey populations, but the modification does not add much to the points we want to make in this paper. Therefore, the model for x(t, z) is

$$\frac{\partial x}{\partial t}(t,z)=x(t,z)\left\{a-cx(t,z)-b\int k(z-z^{\prime })y(t,z^{\prime })d{z}^{\prime }\right\}.$$ (1)

The predator repertoire consumes prey in a degenerate fashion; in the absence of prey it will die at a constant rate α. Therefore, the model for the predator population becomes

$$\frac{\partial y}{\partial t}(t,z)=y(t,z)\left\{-\alpha +\beta \int k(z-z^{\prime })x(t,z^{\prime })d{z}^{\prime }\right\}.$$ (2)

Hence, (1)–(2) constitute our degenerate Lotka–Volterra (dLV) model. Note that given the kernels discussed in the Appendix A, if σ → 0+, (1)–(2) become the classical predator–prey model (except for the fact that each equation represents an infinite repertoire of non-interacting, non-competing continuum of population types):

$$\begin{array}{cc}\hfill \frac{\partial x}{\partial t}(t,z)& =x(t,z)\left\{a\left(1-x(t,z)∕K\right)-by(t,z)\right\},\hfill \\ \hfill \frac{\partial y}{\partial t}(t,z)& =y(t,z)\left\{-\alpha +\beta x(t,z)\right\}.\hfill \end{array}$$

Derivation of the degenerate Verhulst (dV) model

Despite the initial simplicity of the classical logistic growth model of Verhulst in comparison with classical Lotka–Volterra model, derivation of the degenerate case of Verhulst model is conceptually a bit more complex. Consider the original formulation of logistic growth of population y = y(t) by Verhulst (Gabriel et al., 2005):

$$\frac{dy}{dt}=ay-c{y}^2=ay\{1-y∕K\},$$

where a is the net growth rate as in (1), and c, the “friction coefficient,” is a non-negative coefficient reflective of internal competition for resource, implicitly representing the limited amount of resource. For the traditional alternative way of writing this equation, K = a/c is the population's carrying capacity within the particular ecosystem, again as expressed in (1). In this classical non-degenerate case, each member of the population has “equal rights” for a unit of resource, reflective in the y² term that represents pairwise competitive encounters between the members of the population.

To model the “friction” between elements of the population in the dV model, consider two consumers located at z and z′. Similarly to the dLV model above, the consumption of resource is degenerate. Therefore, both y(t, z) and y(t, z′) may compete for resource located at z″; the interactions between the resource and consumers is again described by a kernel functions k(|z″ – z|) and k(|z″ – z′|), with properties expressed in the previous subsection. Then, the “friction” between any given pair of consumers is B(z, z′, z″)k(z″ – z)y(t, z)k(z″ – z′)y(t, z′). Of important notice, for each pair y(t, z) and y(t, z′) interacting through competition for the same resource at z″, the friction coefficient B, expressed in terms of a rate per unit population, may depend on z, z′, and z″. The dependence of B on z and z′ would be reflective of the intrinsic differences in resource consumption between the populations located at z and z′, whereas the dependence on z″ is implicitly reflective of the amount of resource at that location. To minimize the complexity of the model, consider the case when the demand for resource per unit of consumer is independent of the consumer's location. In other words, let B = B(z″) depend at most on resource distribution; the larger B(z″) is the more fierce the competition is, reflective of less resource at z″. Then, the overall friction between a specific y(t, z) and all other y(t, z′) in all locations z″ is

$$\int k(z^{″}-z)y(t,z)\int B\left(z^{″}\right)k(z^{″}-z^{\prime })y(t,z^{\prime })d{z}^{\prime }d{z}^{″}=y(t,z)\int y(t,z^{\prime })\int B\left(z^{″}\right)k(z^{″}-z)k(z^{″}-z^{\prime })d{z}^{″}d{z}^{\prime }.$$

For simplicity, consider a piecewise constant distribution of resource in Z, where Θ is the Heaviside function: Θ(x) = 1 for x ≥ 0, and Θ(x) = 0 for x < 0. Thus,

$$B\left(z^{″}\right)=B_0+B_1ϴ(r-\mid z^{″}\mid )=\{\begin{array}{cc}{B}_0+B_1\hfill & -r\le z^{″}\le r,\hfill \\ B_0\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$

Then,

$$\begin{array}{cc}\hfill \int B\left(z^{″}\right)k(z^{″}-z)k(z^{″}-z^{\prime })d{z}^{″}& =B_0\int k(z^{″}-z)k(z^{″}-z^{\prime })d{z}^{″}+B_1{\int }_{-r}^{r}k(z^{″}-z)k(z^{″}-z^{\prime })d{z}^{″}\hfill \\ \hfill & =B_0{g}_0(z-z^{\prime })+B_{1}g(z,z^{\prime }).\hfill \end{array}$$

We can write g₀ as a function of the single variable z – z′ due to the kernels used and due to a calculation in the Appendix A. The definition of g in case of Gaussian $k\left(z\right)=e^{-z^2∕{\sigma }^2}∕\sigma \sqrt{\pi }$ is the following:

$$g(z,z^{\prime })=\frac{e^{-{(z-z^{″})}^2∕2{\sigma }^2}}{\sigma \pi \sqrt{2}}{\int }_{-\frac{\sqrt{2}}{\sigma }(r+z^{\prime }+\frac{z-z^{\prime }}{2})}^{\frac{\sqrt{2}}{\sigma }(r-z^{\prime }-\frac{z-z^{\prime }}{2})}{e}^{-s^2}ds.$$

Therefore, the dV model becomes

$$\frac{\partial y}{\partial t}(t,z)=ay(t,z)-y(t,z)\int y(t,z^{\prime })(B_0{g}_0(z-z^{\prime })+B_{1}g(z,z^{\prime }))d{z}^{\prime }.$$ (3)

3. Analytical and numeric solutions of dLV

Next consider the model equations (1)–(2). Besides the extinction cases for both x and y, we have

$$(x,y)=(x_{\mathrm{s}},y_{\mathrm{s}})=(\alpha ∕\beta ,(a∕b)(1-c\alpha ∕\alpha \beta )).$$ (4)

In the rest of the paper we assume

$$\alpha ∕\beta <a∕c=K.$$ (5)

That is, the intrinsic predator death rate in the absence of prey must be less than the product of the region's prey carrying capacity and the predator's growth rate (for each predator type).

Stability of the equilibrium state (4)

For stability of (4), we linearize about this state; that is, let

$$y(t,z)=y_{\mathrm{s}}+\epsilon Y\left(z\right)e^{\mu t},x(t,z)=x_{\mathrm{s}}+\epsilon X\left(z\right)e^{\mu t}.$$

Substituting into the equations and retaining O(ε) terms yields

$$\mu X=-c{x}_{\mathrm{s}}X-b{x}_{\mathrm{s}}\int k(z-z^{\prime })Y\left(z^{\prime }\right)d{z}^{\prime },$$ (6)

$$\mu Y=\beta y_{\mathrm{s}}\int k(z-z^{\prime })X\left(z^{\prime }\right)d{z}^{\prime }.$$ (7)

If we take the Fourier transform (Miles, 1971) of these equations and write them in matrix form, we have

$$M\left(\begin{array}{c}\hfill \widehat{X}\hfill \\ \hfill \widehat{Y}\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill \mu +c{x}_{\mathrm{s}}\hfill & \hfill b{x}_{\mathrm{s}}\widehat{k}\left(\xi \right)\hfill \\ \hfill -\beta y_{\mathrm{s}}\widehat{k}\left(\xi \right)\hfill & \hfill \mu \hfill \end{array}\right)\left(\begin{array}{c}\hfill \widehat{X}\hfill \\ \hfill \widehat{Y}\hfill \end{array}\right)=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}\right).$$ (8)

So, for a non-trivial solution to (8), rates μ must be such that the determinant of M equals 0, giving us the characteristic equation for M, namely

$${\mu }^2+c{x}_{\mathrm{s}}\mu +b\beta x_{\mathrm{s}}{y}_{\mathrm{s}}\widehat{k}{\left(\xi \right)}^2=0.$$ (9)

But the solutions to this quadratic satisfy Re(μ) < 0, implying (linear) stability for (x_s, y_s).

As a note in passing, if we had included degeneracy in the prey interaction, that is, if (1) had been replaced by $\frac{\partial x}{\partial t}(t,z)=x(t,z)\{a(1-\int k_1(z-z^{\prime })x(t,z^{\prime })d{z}^{\prime }∕K)-b\int k(z-z^{\prime })y(t,z^{\prime })d{z}^{\prime }\}$, then (9) would have become

$${\mu }^2+(a{x}_{\mathrm{s}}{\widehat{k}}_1\left(\xi \right)∕K)\mu +\beta b{x}_{\mathrm{s}}{y}_{\mathrm{s}}\widehat{k}{\left(\xi \right)}^2=0,$$ (9 ′)

and the stability of (x_s, y_s) would depend on the type of kernels chosen. If both k and k₁ are of Gaussian (or exponential) type, the solutions to (9′) will have real part negative, i.e. Re(μ(ξ)) < 0 for all ξ, implying stability for (x_s, y_s). But if k₁ is of Heaviside type, then there are ranges of wavenumbers ξ where Re(μ(ξ)) > 0, for which in those intervals (x_s, y_s) is unstable. As an example let k be of Gaussian type, say $k\left(z\right)=e^{-{(z∕\sigma )}^2}∕\sigma \sqrt{\pi }$, then k̂(ξ) = exp(–ξ²σ²/4), and let k₁ be of Heaviside type, so

$$k_1\left(z\right)=(1∕2{\sigma }_1)ϴ({\sigma }_1-\mid z\mid )=\{\begin{array}{cc}1∕2{\sigma }_1\hfill & -{\sigma }_1<z<{\sigma }_1\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}},$$

then k̂₁(ξ) = sin(ξσ₁)/ξσ₁. Hence, there are ranges of wavenumbers where k̂₁(ξ) < 0, namely

$$\frac{(2n-1)\pi }{{\sigma }_1}<\xi <\frac{2n\pi }{{\sigma }_1}\text{or}\frac{-(2n-1)\pi }{{\sigma }_1}<\xi <\frac{-2(n-1)\pi }{{\sigma }_1},\text{for}n=1,2,\dots ,$$ (10)

where Re(μ(ξ)) > 0, and (9) becomes

$${\mu }^2+\frac{a{x}_{\mathrm{s}}}{K}\frac{\text{sin}\left({\sigma }_1\xi \right)}{{\sigma }_1\xi }\mu +\beta b{x}_{\mathrm{s}}{y}_{\mathrm{s}}\text{exp}(-{\sigma }^2{\xi }^2∕2)=0.$$

In calculations we will stick with the model (1)–(2) and to these specific kernel functions, though there are many representations we could use. The main difference between the two classes is that the Heaviside model, as opposed to the Gaussian (or exponential case), has only local influence.

Discrete time problem

To motivate further analysis, let t = t_n = nΔt, x_n(w) ≅ x(t_n, w), y_n(z) ≅ y(t_n, z), n = 0, 1, . . . . An interesting case occurs when the kernel is local; that is, let

$$k\left(z\right)=\left(\frac{1}{2\sigma }\right)ϴ(\sigma -\mid z\mid ),$$

where σ > 0 is meant to be rather small. Then (1), (2) become

$$x_{n+1}\left(z\right)=(1+a\Delta t)x_n\left(z\right)-c\Delta t{x}_n{\left(z\right)}^2-\frac{b\Delta t}{2\sigma }{x}_n\left(z\right){\int }_{2-\sigma }^{z+\sigma }{y}_n\left(w\right)dw,$$ (11)

$$y_{n+1}\left(z\right)=(1-\alpha \Delta t)y_n\left(z\right)+\frac{\beta \Delta t}{2\sigma }{y}_n\left(z\right){\int }_{z-\sigma }^{z+\sigma }{x}_n\left(z^{\prime }\right)d{z}^{\prime }.$$ (12)

Let us consider a few analytically tractable special cases. First, let x₀(z) ≡ x* ∈ (0, K), y₀(z) ≡ y* > 0, for all $z\in Z=\Re$. It is straightforward to show that x_n and y_n do not depend on z and that

$$x_{n+1}=x_n\{1+a\Delta t-c\Delta t{x}_n-b\Delta t{y}_n\},$$ (13)

$$y_{n+1}=y_n\{1-\alpha \Delta t+\beta \Delta t{x}_n\}.$$ (14)

The system has the fixed point (x_s, y_s), given in (4), which is stable via the necessary and sufficient conditions of Jury (1971) because of (5) and Δt being small. Also, one can show that (x_n, y_n) → (x_s, y_s) as n → ∞. If we had substituted a Gaussian kernel function above in place of the Heaviside function, we would have obtained the same system (13)–(14).

Next consider the case x₀(z) = x*Θ(z), and y₀(z) ≡ y* > 0 small. This is an idealization of a situation where there is a sharp transition between having a competing population and having no population (i.e. no resource for y), perhaps representing the edge of a population patch. Then, as long as z ≥ σ , (13)–(14) hold and (x_n, y_n) → (x_s, y_s) as n → ∞. For z ≤ –σ, x_n ≡ 0 and y_n = (1 – αΔt)ⁿ y* → 0 as n → ∞. Also, if we let z → 0+, then it can be shown that, with a slight abuse of notation, letting x_n = x_n(0+), y_n = y_n(0+),

$$\begin{array}{cc}\hfill x_{n+1}& =x_n\left\{1+a\Delta t-c\Delta t{x}_n-\frac{b\Delta t}{2\sigma }{\int }_{-\sigma }^{\sigma }{y}_n\left(z^{\prime }\right)d{z}^{\prime }\right\}\hfill \\ \hfill & =x_n\{1+a\Delta t-c\Delta t{x}_n-b\Delta t{y}_n\},\hfill \end{array}$$ (15)

$$\begin{array}{cc}\hfill y_{n+1}& =y_n\left\{1-\alpha \Delta t+\frac{\beta \Delta t}{2\sigma }{\int }_0^{\sigma }{x}_n\left(z^{\prime }\right)d{z}^{\prime }\right\}\hfill \\ \hfill & =y_n\left\{1-\alpha \Delta t+\frac{\beta \Delta t}{2}{x}_n\right\},\hfill \end{array}$$ (16)

and in this case (x_n, y_n) → (2α/β, (a/b)(1 – 2cα/aβ)) as n → ∞, assuming K > 2α/β. So, at the population edge (from the trait z viewpoint), the prey population has competition only on one side, so it can reach a density twice what it can in the “interior.” This suggests that for 0 < z < σ, x_n(z) will converge to a value in the interval (x_s, 2x_s), though this does not indicate the possibility of any fine structure like possible oscillations in population. The predator population sizes will follow the structure variation of the prey populations except for a “phase” shift. If we let z → σ+, expressions (15), (16) can be re-derived so that (x_n(σ+), y_n(σ+)) → (x_s, y_s)) as n → ∞. For this case, where Gaussian kernels are used instead of Heaviside kernels, the analytic situation is readily more complex to deal with. For example, for z < 0, x_n(z) ≡ 0, but at $t=\Delta t,y_1\left(z\right)=\left(y^{\ast }\right)\{1-\alpha \Delta t+\frac{\beta \Delta t}{2}\left(x^{\ast }\right)\mathrm{erfc}(-z∕\sigma )\}$, where erfc(·) is the complimentary error function replace erfc(–z/σ) with e^z/σ in the exponential kernel case), then iterations have analytically complicated dependence on z, which does not make them easily tractable. Instead, we next carry out numerical simulations using Gaussian kernels.

Simulating the degenerate Lotka–Volterra (dLV) and degenerate Verhulst (dV) models

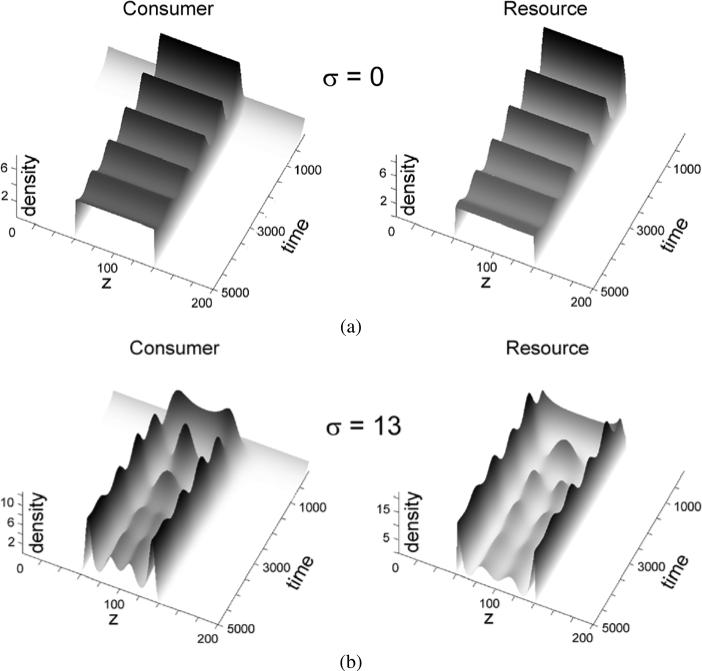
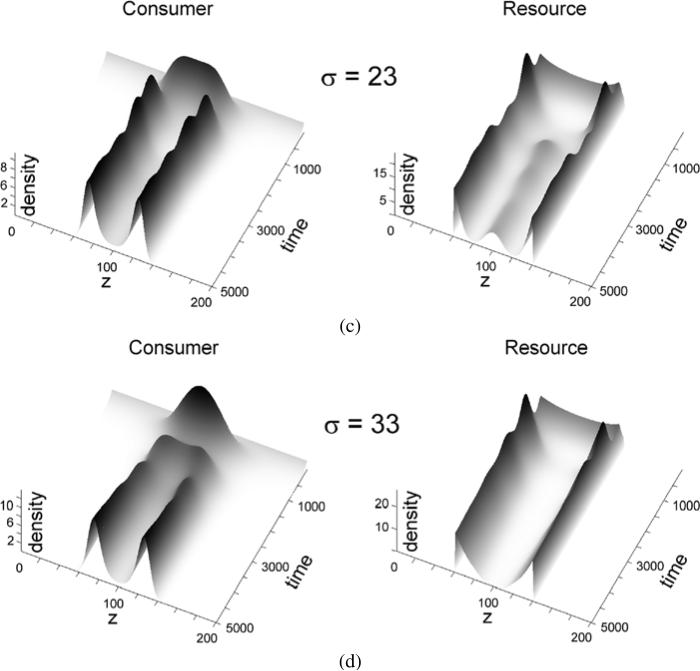
As the first example, we took k(z) to be Gaussian kernel function, with σ left variable. In Fig. 1, when σ = 0, there is no degeneracy in the model and, as expected, convergence of y(t, z) is limited to the prey food source, given by x(0, z) = 5Θ(140 – z)Θ(z – 60), that is, a rectangular distribution with amplitude 5 in the interval 60 < z < 140. The predator population at t = 0 is uniformly distributed at a very low density initially in all the graphs of Fig. 1.

Fig. 1.

Simulation results of consumer dynamics in the system (1)–(2) for the parameters a = 1, b = 0.2, c = 0.02, α = 0.5, β = 0.12, and indicated values of sigma. The non-degeneracy case is represented by σ = 0.

The resource x in Fig. 1 had a rectangular distribution with amplitude of 5 in the interval [60; 140]. In the absence of degeneracy (σ = 0), consumers located at each preference point z interact with resource independently of each other, resulting in a series of independent classical Lotka–Volterra models. This implementation of the model manifested, as expected, in consumer dynamics that were similar at all preference points z in the interval matching the distribution of resource (upper left panel in Fig. 1). Considering that resource is self-limiting, as reflected in the term c in Eq. (1), the dynamics of consumer converged with time towards a stable solution, as expected in the classical competitive Lotka–Volterra model.

Very different dynamics were observed when the interactions between resource and consumer were degenerate (σ ≠ 0). Consider the case of σ = 33 (Fig. 1). The population of consumers dynamically separated into two clearly defined subpopulations. The explanation for such divergence by preference is as follows. Due to the degenerate interaction between resource and consumers at all preference points, the consumers with preferences z and z′ will compete not only among their own kind (other consumers with preference z or preference z′), but also with each other, for resource located at various z″. Initially, when the overall resource is abundant, the population grows rapidly in the middle of the resource distribution, because the consumers located here have resources from both sides of the distribution available to them due to the degenerate nature of consumption. The consumers with resource preferences that are closer to the edges of the resource distribution are at a competitive disadvantage, and grow slower because less overall resource is available to them. However, when the consumer population grows significantly, the strength of competition for resource will be greatest in the middle of the resource distribution, due to the degenerate interaction of resource with consumers. As a result, consumers with resource preferences in the middle of the distribution range experience the fiercest competitive pressure and become negatively selected, pushing the “wings” of the population distribution to the sides of the distribution range. Considering again the simple example of foliage distribution by altitude, zebras and giraffes consume foliage at different altitudes, but there are no species with intermediate heights between these two. This observation appears counterintuitive, because there is foliage available at the altitudes above those commonly grazed by zebras and below those commonly grazed by giraffes. The results of our model suggest that the intermediate forms are likely suppressed by the degeneracy-based competition, on the one side from zebras who can reach higher than their average height, and on the other side from giraffes who can reach lower than their average height. Applied to immunology, our model suggests that various antigens will not necessarily elicit generation of B or T cells whose specificity matches the antigens perfectly. Instead, some antigenic determinants will appear “immunodominant,” while the others will seem less antigenic. This difference takes place not because of the intrinsic differences in the “antigenic strength.” Instead, the clumped distribution of the immune cell specificities may have to do with population dynamics within the degenerate repertoires of the immune receptors.

There is a limit, however, to how far the forming subpopulations can be pushed apart, because there is no resource available for consumption outside of the resource distribution range. Therefore, the population stabilizes into two subgroups, as shown in the lower right panel of Fig. 1. With smaller values of σ and therefore narrower degeneracy-defined competition ranges, more subpopulations form (σ = 13 in Fig. 1). The results of the model (1)–(2) shown in Fig. 1 closely resemble the results obtained in a different model based on cellular automata whose behavior was defined by degenerate consumption of rectangular distributed resource; no analytical considerations were utilized in that case (Atamas, 1996, 2003).

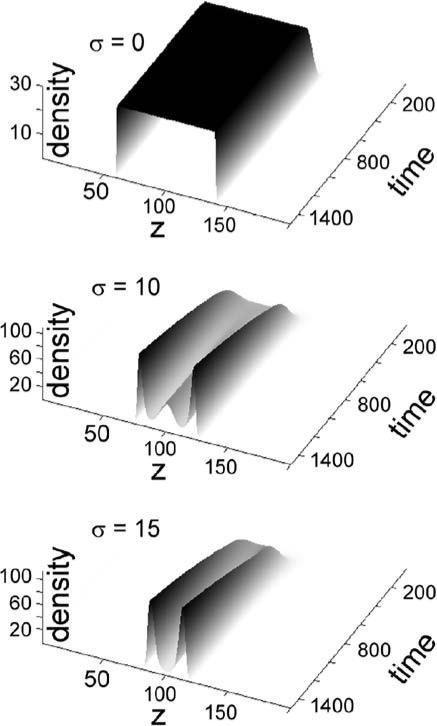
We do not investigate the dV model, that is Eq. (3), analytically here, but the numeric solution shown in Fig. 2 for the dV model resembles the nature of dynamics observed in the dLV model (Fig. 1). Notice that despite the different inherent presumptions between the dLV model (1)–(2) and the dV model (3), the effect of degeneracy on population dynamics in these two models was similar, as well as being similar to that observed in a cellular automata-based model of a degenerate consumer–resource system (Atamas, 1996, 2003).

Fig. 2.

Simulation results of dV model (3) for indicated values of sigma. The parameters were B₀ = 100, B₁ = 0.1, and a = 3. The basic behavior of the model is similar to the dLV model.

4. Discussion

The proposed model demonstrates competition-driven divergence of subpopulations within repertoires of degenerately interacting resource and consumer. Degeneracy is functional microdiversity of individual elements in repertoires. It occurs at the molecular, cellular, and organismal levels. Degeneracy greatly increases the adaptability through selection and also leads to phenomenal reliability, because a loss of an individual element will have a small impact on the whole repertoire, due to the overlapping functionality of multiple elements (Atamas et al., 1998; Atamas, 1996, 2003; Edelman and Mountcastle, 1978; Edelman and Gally, 2001). In the proposed model, the scale, or “width,” of degeneracy is defined by σ. In the non-degenerate case (σ = 0, see Fig. 1), the population of consumers simply mirrors the resource population. However, when degeneracy is introduced (σ > 0, see Fig. 1), the population undergoes dynamic self-structuring.

Our model is based on the novel concept of degeneracy, which is broadly applicable to various selective systems, including molecular, cellular, and organismal selection of degenerate repertoires. The results demonstrate the relevance of Darwin's original thought experiment on “divergence of character.” Although Darwin did not call it a “degenerate system” and only made a thought experiment, he was the first to suggest that such a system could be at work in the case of species formation, noting that “competition will generally be most severe between those forms which are most nearly related to each other in habits, constitution, and structure” (Darwin, 1859). Our quantitative modeling takes these ideas further by providing a framework for quantifying the limits of how far the forming sub-populations can be pushed apart. The Darwin's thought experiment describes an outcome similar to that observed in our steady-state scenario, and we take it further by providing visual demonstration of the intermediate progression of the speciation. However, the most notable, novel, development that we propose in this study is that degeneracy leads to a phenomenon that was not foreseen by Darwin in his thought experiment—the phenomenon of non-local influences in the degenerate systems. Degeneracy, by definition, is the ability of each single individual in a population to manifest a spectrum (distribution), not a single static measure, of a trait. As a result, a population becomes an ensemble of overlapping degeneracy ranges. A change in the quantity of individuals of any given kind will not only affect their immediate competition within their degeneracy range, but will have global effect on the population as a whole. The model proposed here allows for numerical exploration of this phenomenon.

The results demonstrate that the system's behavior appears to depend strongly on the width of the degeneracy range for the interactions between resource and consumer. The elements of the consumer repertoire with overlapping preference ranges for the resource (adjacent in the Z domain), will interact and be selected by the same signals (resource) from the environment. Therefore, the consumers with overlapping degeneracy ranges will directly compete for resource. Moreover, even if two elements have “degeneracy ranges” that do not directly overlap, they might overlap with a common third element of the repertoire. Therefore, numeric expansion or attenuation of a single element will affect not only its immediate “neighbors on Z” but the whole repertoire.

Of important notice, edges of resource distribution define the behavior of the degenerate selective system. In a realistic ecological system with geographic nature of preference z (space), such as forests, edge effects are obvious (Schedlbauer et al., 2007; Malcolm, 1994). Simple considerations predict that, indeed, this should be the case. First, consumers sited at the edges have less overall potential for the amount of recognized resource. This leads to earlier completion of density fluctuation cycles at the edges than in the middle of distribution. On the other hand, edge-sited consumers also experience less competition from the neighboring consumers, simply because they have fewer neighbors. Thus, the denser zones in distributions should be “pushed apart” to the edges. This does happen in fact in Figs. 1 and 2. The realistic Z axis of resource preference should not be necessarily geographic. For example, experimental observation of such separation to the edges of distribution has been made for two sympatric species of leaf-eating crabs in a rain forest (Greenaway and Raghaven, 1998). Although the two species of crabs can apparently utilize each other's preferred types of leaves, they specialize in consumption of leaves of different quality. In this case, the sympatric (occupying the same geographic location) species are using the opposed ends of the leaf litter quality.

Importantly, the proposed model is applicable to degenerate repertoires in a broad sense (not just classical ecosystems), such as repertoires of molecules (e.g. enzymes and their substrates, cytokines and their receptors) or cells (e.g. T and B lymphocytes and infectious invaders). Any selective system demonstrating functional plasticity of elements may qualify as a degenerate system. As a mater of fact, degeneracy is a consequence of structural and functional plasticity of elements of diverse repertoires. Synaptic plasticity exemplifies degeneracy in the nervous system (Edelman and Gally, 2001; Leonardo, 2005). Structural and the subsequent ligand-binding plasticity of proteins exemplify degeneracy in molecular systems (Atamas, 2005). Degeneracy of immune specificities arises from the plasticity at the antigen-combining sites of antibodies (Manivel et al., 2002; Goel et al., 2004) and T cells (Selin et al., 2004). The origin of a new direction of adaptive evolution starts with a population of variably responsive, developmentally plastic organisms (West-Eberhard, 2005). The results of our model show that degeneracy in turn affects the environmental responsiveness, or plasticity, of biological repertoires. The results show that the originally homogeneously distributed populations become dynamically divergent within the resource distribution range. This is an unexpected result from the perspective of naïve Darwinism defined as “survival of the fittest.” In the latter case, being “the fittest” implies that plasticity would lead the consumer population to mirror the distribution of resource (the only “environment” in this model) on the Z axis. In contrast, our results show that degeneracy leads to a fitness landscape (reproductive success along the Z axis) of the consumer that is very different from the simple rectangular distribution of resource (see Figs. 1 and 2).

From ecological perspective, these ideas appear important as a possible mechanism of sympatric, as opposed to allopatric, divergence in ecosystems. The entire idea of sympatric divergence implies, in contrast to allopatric divergence, that there is no geographic isolation between elements of the repertoire (a species or a subpopulation in an ecosystem). The proposed model has no particular isolating mechanism for the elements of the repertoire, yet with time, parts of the repertoire become dynamically isolated. The repulsion of appearing subpopulations is due to competition for the resource not only between consumers of the same specificity, but also between consumers adjacent in Z. Such self-structuring of the recognizing population leads to the structuring of the resource, and the structured resource further supports the structuring of the consumer population (see Fig. 1). This model suggests a mechanism of sympatric divergence of subpopulations based purely on ecodynamic isolation.

A strength and also a limitation of the proposed models is that they do not include sexual reproduction-based selection or genetic mutability in the repertoires. As a strength, since no sexual reproduction and no genetic mutability is present in the system (the preference z remains the same for each growing element of the repertoire), the models are applicable to a variety of non-sexually expanding and immutable degenerate repertoires (such as antigen-driven expansion of lymphocytes, or selective synaptic strengthening of connections selected by signals in neuronal circuits). Also, regarding the strength, the models show that even in the absence of Darwinian variation through mutations, selection alone leads to pattern formation in degenerate repertoires. However, the applicability of the models would be obviously limited for sexually reproducing species in ecological systems, and for selective processes that are based on hypervariability of the offspring, such as in specificity maturation of B cells.

In summary, we have proposed a model of generalized selective degenerate repertoires that display self-structuring dynamics. It is an example where non-local interactions between populations of one kind or another are extremely important, and the modeling leads to (non-linear) partial differential-integral equations. Other areas where such non-local effects have recently been modeled include non-local contact models of infectious diseases, and modeling of non-local connectivity in neural field studies, though in these cases, z represents a spatial variable. Needless to say, biology has provided a need to further analyze the behavior of classes of these type equations with non-local integral terms, and at present analytic results are quite limited.

Appendix A: The kernel functions used in the paper

Examples of the kind of kernels we consider here include a Gaussian form, namely $k\left(z\right)=\text{exp}(-z^2∕{\sigma }^2)∕\sigma \sqrt{\pi }$, where σ is a variance parameter, and a Heaviside form, namely k(z) = σ/2 if |z| < σ, and 0 otherwise. (Defining the usual Heaviside function, or unit step function, as Θ(z) = 1 if z ≥ 0, and 0 for z < 0, then another way of writing k(z) is (σ/2)Θ(σ – |z|).) Both of the kernel forms belong to a larger class of functions that are proportional to exp(–|z/σ|^r). In the Gaussian case, r = 2, while letting r → ∞, we obtain the Heaviside form. As σ → 0+, both Gaussian and Heaviside forms of the kernel function approximate Dirac delta functions; thus, in the limit, this would imply non-interacting, non-competing, continuum of population types.

For the dV model we needed to show that the integral for $g(z-z^{″})=\int k(z^{\prime }-z)k(z^{\prime }-z^{″})d{z}^{\prime }$ in Section 2 can actually be written as a single variable z – z″ for at least the kernels used in the paper. The integrals are over the whole real line ℜ. First, given $k\left(z\right)=\frac{\text{exp}(-z^2∕{\sigma }^2)}{\sigma \sqrt{\pi }}$, then

$$\begin{array}{cc}\hfill \int k(z^{\prime }-z)k(z^{\prime }-z^{″})d{z}^{\prime }& =\frac{1}{\pi {\sigma }^2}\int \text{exp}(-[{(z^{\prime }-z)}^2+{(z^{\prime }-z^{″})}^2]∕{\sigma }^2)d{z}^{\prime }\hfill \\ \hfill & =\frac{1}{\pi {\sigma }^2}\int \text{exp}(-[{(z^{\prime }-z^{″}-x)}^2+{(z^{\prime }-z^{″})}^2]∕{\sigma }^2)d{z}^{\prime },\hfill \end{array}$$

where z = z″ + x. Now, with y = z′ – z″,

$${(z^{\prime }-z^{″}-x)}^2+{(z^{\prime }-z^{″})}^2=2y^2+x(x-2y)=2{(y-x∕2)}^2+x^2∕2.$$

Thus, the integral becomes

$$\begin{array}{cc}\hfill \frac{\text{exp}(-x^2∕2{\sigma }^2)}{\pi {\sigma }^2}\int \text{exp}(-2{(y-x∕2)}^2∕{\sigma }^2)dy& =\frac{\sqrt{2}}{\pi \sigma }\text{exp}(-x^2∕2{\sigma }^2){\int }_0^{\infty }\text{exp}(-r^2)dr\left(r=\left(y-\frac{x}{2}\right)\frac{\sqrt{2}}{\sigma }\right)\hfill \\ \hfill & =\frac{\text{exp}(-x^2∕2{\sigma }^2)}{\sigma \sqrt{2\pi }}=\frac{\text{exp}(-{(z-z^{″})}^2∕2{\sigma }^2)}{\sigma \sqrt{2\pi }}.\hfill \end{array}$$

That is, the integral is actually of Gaussian form, of argument z – z″.

Similarly, suppose k is of Heaviside form, that is, $k\left(z\right)=\frac{1}{2\sigma }ϴ(\sigma -\mid z\mid )$. Then $\int k(z^{\prime }-z)k(z^{\prime }-z^{″})d{z}^{\prime }=0$ unless |z′ – z| < σ and |z′ – z″| < σ; that is, unless |z – z″| < 2σ. If this is so, then integral equals $\frac{2\sigma -\mid z-z^{″}\mid }{4{\sigma }^2}$. Hence,

$$\int k(z^{\prime }-z)k(z^{\prime }-z^{″})d{z}^{\prime }=\frac{2\sigma -\mid z-z^{″}\mid }{4{\sigma }^2}ϴ(2\sigma -\mid z-z^{″}\mid ).$$

While this shows g = g(z – z″), g is not a Heaviside step function. Nevertheless, it is a “tent-like” form with compact support (i.e. is zero outside an interval about its argument), so it preserves the local character of the Heaviside k.

To summarize,

k(z)	k̂(ξ)	g(z)	ĝ(ξ)
$\frac{\text{exp}(-z^2∕{\sigma }^2)}{\sigma \sqrt{\pi }}$	exp(–σ2ξ2/4)	$\frac{\text{exp}(-z^2∕2{\sigma }^2)}{\sigma \sqrt{2\pi }}$	exp(–σ2ξ2/2)
$\frac{1}{2\sigma }ϴ(\sigma -\mid z\mid )$	$\frac{\text{sin}\left(\sigma \xi \right)}{\sigma \xi }$	$\frac{2\sigma -\mid z\mid }{4{\sigma }^2}ϴ(2\sigma -\mid z\mid )$	$\frac{2}{{\xi }^2}(1-\text{cos}\left(2\sigma \xi \right))$
$\frac{\text{exp}(-\mid z\mid ∕\sigma )}{2\sigma }$	$\frac{1}{1+{\sigma }^2{\xi }^2}$	$\frac{\text{exp}(-\mid z\mid ∕\sigma )}{4\sigma }(1+\frac{\mid z\mid }{\sigma })$	$\frac{1}{1+2{\sigma }^2{\xi }^2+{\sigma }^4{\xi }^4}$