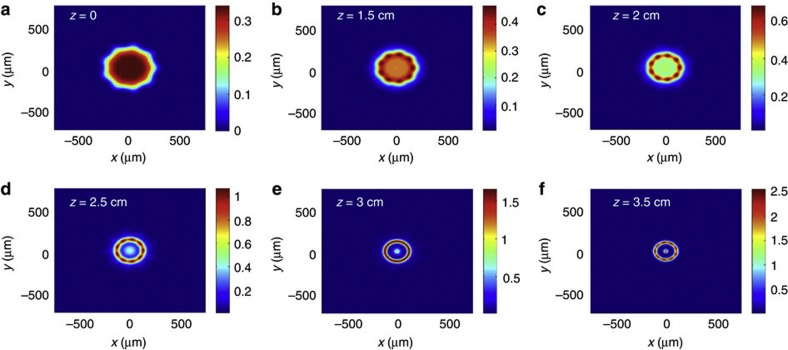
Figure 5. NLSE simulation illustrating topological changes of a relativistically self-focusing laser pulse.

The colour bars indicate the squared laser strength parameter a². The laser pulse evolves according to the NLSE in a plasma of density n_e=5 × 10¹⁷ cm⁻³. (a) Initial pulse at z=0 with azimuthally modulated super-Gaussian profile. Algebraic form and parameters are given in Methods. (b,c) The azimuthal perturbations quickly evolve into distinct hotspots by z=2 cm, similar to those present in the actual laser pulse. (d,e) Hotspots then evolve into a nearly cylindrically symmetric ring by z=3 cm, as the central peak intensifies. At this point, the radial profile is very similar to that of initially cylindrically symmetric super-Gaussian pulses, as shown in Fig. 4b. (f) By z=3.5 cm, the central peak becomes more intense than the outer ring. WAKE simulations of similar profiles suggest that this central peak continues intensifying rapidly, eventually forming a rapidly evolving bubble into which surrounding plasma electrons inject. At z=3.5 cm, however, the density perturbation has already become substantial, invalidating further description by the NLSE.