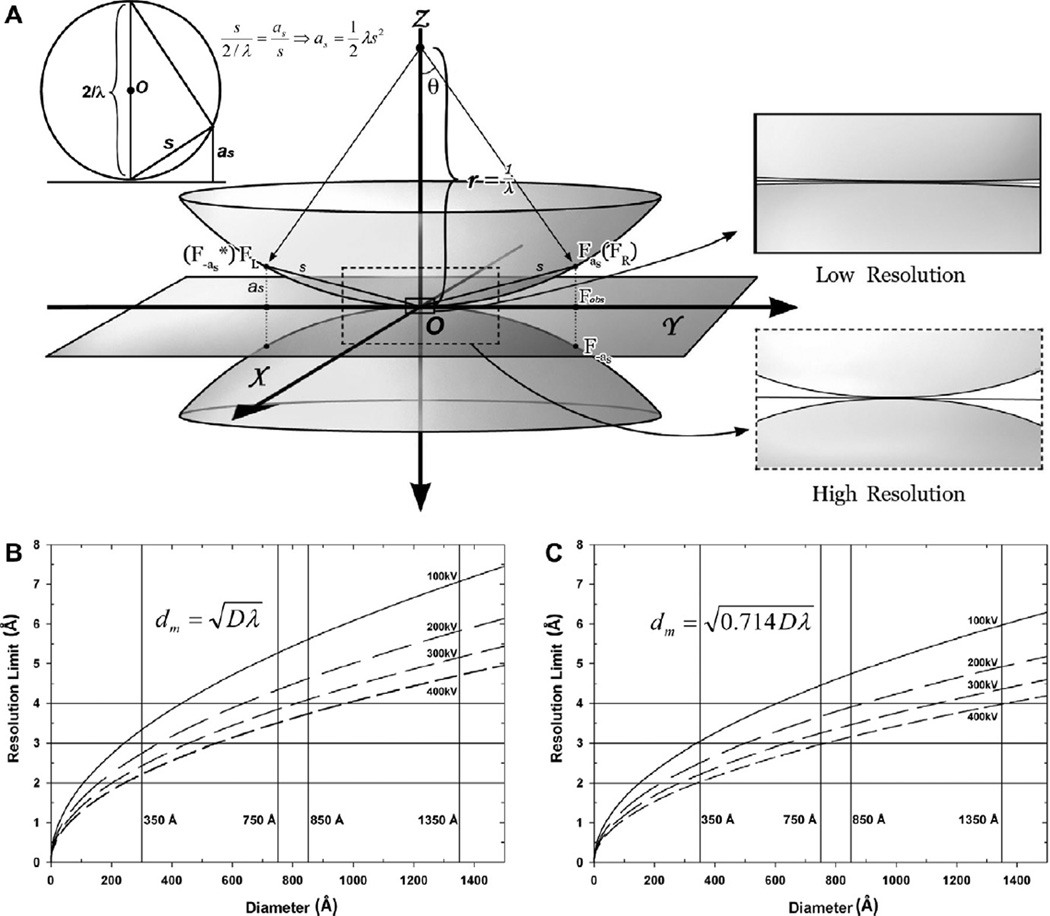
Fig. 3.
Breakdown of the Central Projection Theorem and its limit on the resolution of 3D reconstruction. (A) Illustration of the characteristic surfaces concept in 3D Fourier space. The 2D Fourier transform of a cryoEM image is shown as a flat 2D plane at Z = 0. According to the Central Projection Theorem, this plane is equivalent to the central section of the 3D Fourier transform (i.e., structure factors) of the specimen. When approaching atomic resolution, particularly for large particles, this theorem is no longer valid due to convolution of many contrast transfer functions, each at a different focus value for slices at different heights in the particle. Instead, each Fourier coefficient of the image is the sum of two structure factors, located, respectively, on the top and bottom characteristic surfaces at (X, Y, as) and (X, Y, −as), as described in the text. The upper left inset illustrates that each characteristic surface is a sphere with radius = 1/λ, equivalent to the Ewald sphere (upper left inset). s denotes the spatial frequency at point (X, Y, Z). On the characteristic surfaces, Z is either as (upper surface) or −as (lower surface). The two right insets illustrate that at low resolution, the characteristic surfaces merge into a single, nearly flat section, corresponding to the central section described in the Central Projection Theorem. (B–C) Resolution limit imposed by the Central Projection Theorem at different accelerating voltages based on formulas by Spence (Spence, 1988) (B) and by DeRosier (DeRosier, 2000) (C). The four vertical lines in (B) and (C) indicate typical particle diameters, and the three horizontal lines indicate resolution limits from 2 to 4 Å.