One Component? Two Components? Three? The Effect of Including a Non-Exchanging ‘Free” Water Component in Multicomponent Driven Equilibrium Single Pulse Observation of T1 & T2 (mcDESPOT)

Abstract

Quantitative myelin content imaging provides novel and pertinent information related to underlying pathogenetic mechanisms of myelin-related disease, or disorders arising from aberrant connectivity. Multicomponent Driven Equilibrium Single Pulse Observation of T₁ and T₂ (mcDESPOT) is a time-efficient multicomponent relaxation analysis technique that provides estimates of the myelin water fraction (MWF), a surrogate measure of myelin volume. Unfortunately, mcDESPOT relies on a two water-pool model (myelin-associated water, and intra/extra cellular water), which is inadequate within partial-volume voxels, i.e. containing brain tissue and ventricle or meninges, resulting in MWF under-estimation. To address this, a third, non-exchanging ‘free-water’ component was introduced to the mcDESPOT model. Numerical simulations and experimental in vivo data show the model to perform advantageously within partial volume regions whilst providing robust and reproducible results. It is concluded that this model is preferable for future studies and analysis.

Introduction

Non-invasive assessment of myelin content provides salient information in de and dys-myelinating disorders as well as in neurological and psychiatric disorders suspected of arising from altered brain connectivity. Multi-component analysis of relaxation data (MCR) provides a surrogate measure of myelin volume through a quantitative metric, termed the myelin water fraction, and defined as the proportion of water trapped within the lipid bilayers of the myelin sheath relative to the total water contained within the imaging voxel (1). Prior work examining myelin water fraction estimates derived from T₂ decay data of normal and pathological tissue have demonstrated strong correlations with histological myelin content assessments (2,3), demonstrating its utility in investigations of white matter pathology (4-6). Unfortunately, conventional multiple-echo T₂ techniques are time consuming and requiring lengthy scan times (i.e. 16 minutes for approx. 8-12 contiguous slices) (7).

mcDESPOT (multi-component Driven Equilibrium Single Pulse Observation of T₁ and T₂) (8), is an alternative MCR approach that affords improved time efficiency and the ability to acquire whole-brain data in clinically feasible scan times. Whilst T₂-based approaches derive the myelin water fraction from a series spin-echo measurements acquired over an echo time range, mcDESPOT utilizes a series of spoiled gradient echo (SPGR, spoiled FLASH) and fully-balanced steady-state free precession (bSSFP) data acquired over a range of flip angles. Additional acquisitions may be included to correct for main (B₀) and transmit (B₁) magnetic field inhomogeneities (9). To calculate the myelin water fraction, SPGR and bSSFP signal models incorporating two exchanging water pools (water trapped within the myelin sheath; and a combined pool comprised of water inside and outside the myelinated axons, together termed the intra/extra-cellular, IE, water) are fit to the data.

Though some groups have sought to resolve the signal from water within the axon (axonal water), from that outside the axon (extra-axonal water) through additional data acquisition or inclusion of T₁ information (10, 11), conventional T₂ analysis reliably provides two independent pools within white matter (1).

Voxels containing heterogeneous tissues, for example containing portions of brain tissue and ventricle or meninges, or within necrotic ‘black holes’ and tumors, may not be suitable modeled using a straight-forward two-component model. In these areas, the very slow relaxing ‘free’ water (i.e., the cerebral spinal fluid within the ventricles) is not adequately accounted for by mcDESPOT, potentially causing under-estimation of the myelin water fraction and/or over-estimation of each pool’s T₁ and T₂ values. In these regions it is logical to include a third, non-exchanging, water pool into the mcDESPOT model.

In this paper, we describe the inclusion of a third non-exchanging and slowly-relaxing water pool into the SPGR and bSSFP signal models. Through numerical simulations, we investigate the accuracy and precision of this three-pool model compared to the prior two-pool approach. The simulation results are confirmed in vivo using experimental results from a broad range of participants, and the method’s reproducibility is evaluated using repeated scans of the same individual. Results show the three-pool model provides more robust myelin water fraction estimation in partial volume areas, particularly in regions bordering brain tissue and the ventricles and meninges with high reproducibility.

Theory

3 Pool Model

As presented previously (12-14), the two-component steady-state SPGR and bSSFP magnetizations ( $M_{\mathit{SPGR}}^{\mathit{SS}}$ and $M_{\mathit{bSSFP}}^{\mathit{SS}}$) are written in matrix notation as

$$M_{\mathit{SPGR}}^{\mathit{SS}}={(I-e^{A_{\mathit{SPGR}}\times \mathit{TR}}\cos \alpha )}^{-1}\times M_{\mathit{SPGR}}(I-e^{A_{\mathit{SPGR}}\times \mathit{TR}})\sin \alpha$$ [1]

and

$$M_{\mathit{bSSFP}}^{\mathit{SS}}={\left[I-e^{A_{\mathit{bSSFP}}\times \mathit{TR}}R(\alpha )\right]}^{-1}\times (e^{A_{\mathit{bSSFP}}\times \mathit{TR}}-I)A_{\mathit{bSSFP}}^{-1}C,$$ [2]

where I is the identity matrix, and M_SPGR, M_bSSFP, A_SPGR, A_bSSFP, C and R(α) are matrices containing the relative water pool volume fraction, relaxation, off-resonance, exchange rate, and excitation flip angle terms defined in Appendix A. $M_{\mathit{SPGR}}^{\mathit{SS}}$ and $M_{\mathit{bSSFP}}^{\mathit{SS}}$ are column vectors containing the x, y and z components of the steady-state magnetization,

$$M_{\mathit{SPGR}}^{\mathit{SS}}={\left[M_{z,M}^{\mathit{SPGR},\mathit{SS}},M_{z,\mathit{IE}}^{\mathit{SPGR},\mathit{SS}}\right]}^T$$ [3]

and

$$M_{\mathit{bSSFP}}^{\mathit{SS}}={\left[M_{x,M}^{\mathit{bSSFP},\mathit{SS}},M_{x,\mathit{IE}}^{\mathit{bSSFP},\mathit{SS}},M_{y,M}^{\mathit{bSSFP},\mathit{SS}},M_{y,\mathit{IE}}^{\mathit{bSSFP},\mathit{SS}},M_{z,M}^{\mathit{bSSFP},\mathit{SS}},M_{z,\mathit{IE}}^{\mathit{bSSFP},\mathit{SS}}\right]}^T.$$ [4]

The M and IE subscripts denote the myelin-associated and intra/extra-cellular water pools, respectively. T denotes the transpose of the matrix. In the case of SPGR, only the longitudinal magnetization is considered, with the transverse magnetization ideally spoiled prior to each radio-frequency (RF) excitation pulse.

The measured two-component SPGR and bSSFP signals, therefore, are

$$S_{\mathit{SPGR}}^{2-\mathit{Component}}=M_{z,M}^{\mathit{SPGR},\mathit{SS}}+M_{z,\mathit{IE}}^{\mathit{SPGR},\mathit{SS}}$$ [5]

and

$$S_{\mathit{bSSFP}}^{2-\mathit{Component}}=M_{x,M}^{\mathit{bSSFP},\mathit{SS}}+M_{x,\mathit{IE}}^{\mathit{bSSFP},\mathit{SS}}+i\left(M_{y,M}^{\mathit{bSSFP},\mathit{SS}}+M_{y,\mathit{IE}}^{\mathit{bSSFP},\mathit{SS}}\right).$$ [6]

To incorporate a third non-exchanging water pool into these models, we expand the M_SPGR, M_bSSFP, A_SPGR, A_bSSFP, C and R(α) matrices as shown in Appendix B. $M_{\mathit{SPGR}}^{\mathit{SS}}$ and $M_{\mathit{bSSFP}}^{\mathit{SS}}$ are re-defined as

$$M_{\mathit{SPGR}}^{\mathit{SS}}={\left[M_{z,M}^{\mathit{SPGR},\mathit{SS}},M_{z,\mathit{IE}}^{\mathit{SPGR},\mathit{SS}},M_{z,F}^{\mathit{SPGR},\mathit{SS}}\right]}^T$$ [7]

and

$$M_{\mathit{bSSFP}}^{\mathit{SS}}={\left[M_{x,M}^{\mathit{bSSFP},\mathit{SS}},M_{x,\mathit{IE}}^{\mathit{bSSFP},\mathit{SS}},M_{x,F}^{\mathit{bSSFP},\mathit{SS}},M_{y,M}^{\mathit{bSSFP},\mathit{SS}},M_{y,\mathit{IE}}^{\mathit{bSSFP},\mathit{SS}},M_{y,F}^{\mathit{bSSFP},\mathit{SS}},M_{z,M}^{\mathit{bSSFP},\mathit{SS}},M_{z,\mathit{IE}}^{\mathit{bSSFP},\mathit{SS}},M_{z,F}^{\mathit{bSSFP},\mathit{SS}}\right]}^T,$$ [8]

where the F subscript denotes the third non-exchanging ‘free’ water pool.

The three-component SPGR and bSSFP signal, therefore, is given by

$$S_{\mathit{SPGR}}^{3-\mathit{Component}}=M_{z,M}^{\mathit{SPGR},\mathit{SS}}+M_{z,\mathit{IE}}^{\mathit{SPGR},\mathit{SS}}+M_{z,F}^{\mathit{SPGR},\mathit{SS}}$$ [9]

and

$$S_{\mathit{bSSFP}}^{3-\mathit{Component}}=M_{x,M}^{\mathit{bSSFP},\mathit{SS}}+M_{x,\mathit{IE}}^{\mathit{bSSFP},\mathit{SS}}+M_{x,F}^{\mathit{bSSFP},\mathit{SS}}+i\left(M_{y,M}^{\mathit{bSSFP},\mathit{SS}}+M_{y,\mathit{IE}}^{\mathit{bSSFP},\mathit{SS}}+M_{y,F}^{\mathit{bSSFP},\mathit{SS}}\right).$$ [10]

In this model we have assumed the slow-relaxing ‘free’ water pool to be non-exchanging with respect to the T₁ and T₂ times. This is likely a safe assumption for ventricular and meningeal water, which needs to cross the blood-brain barrier before mixing with the tissue water pools.

Discrete Fitting of the 3 Pool Model

To derive estimates of T_1,M, T_1,IE, T_1,F, T_2,M, T_2,IE, T_2,F, M_F, F_F, and τ_M, Eqns. [9] and [10] are fit to acquired multiple flip angle data using a stochastic region contraction (SRC) approach (9, 15). SCR comprises the following 6 steps: 1. Likely value ranges for each free-parameter are first defined; 2) N_S Potential solution sets are then generated by randomly selecting values for each free-parameter from the defined ranges; 3) The least-squares residual for each potential solution is calculated, and the solutions rank-ordered; 4) The top N_T solutions are identified, and the minimum and maximum value of each free parameter contained within this sub-set are determined; 5) The identified minimum and maximum values are used to re-define the possible value ranges (i.e., contracting the search-space); and 6) Return to step #2 and repeat until convergence is achieved or some termination criteria is met.

To fit our models, we define the following. Initial value ranges are: 250ms ≤ T_1,M ≤ 750ms; 250ms ≤ T_1,IE ≤ 3500ms; 1500ms ≤ T_1,F ≤ 7500ms; 0ms ≤ T_2,M ≤ 150ms; 0ms ≤ T_2,IE ≤ 250ms; 150ms ≤ T_2,F ≤ 1000ms; 0.00 ≤ M_F ≤ 0.49; 0.00 ≤ F_F ≤ 0.75; and 25ms ≤ τ_M ≤ 1500ms. Additional constraints, IE_F = 1.00 - (M_F + F_F); and M_F + F_F ≤ 0.95, are imposed. These value ranges were chosen followed consideration of prior literature values (1, 10, 11).

N_S = 5000 sets of <T_1,M, T_1,IE, T_1,F, T_2,M, T_2,IE, T_2,F, M_F, F_F, τ_M> are generated by randomly choosing each parameter from a uniform distribution.

Sum-of-squares residuals are calculated following normalization of the theoretical and acquired data. The SPGR and bSSFP data are independently normalized with respect to their mean values.

From the 5000 <T_1,M, T_1,IE, T_1,F, T_2,M, T_2,IE, T_2,F, M_F, F_F, τ_M> potential solutions, the top N_T = 50 sets are used to contract each parameter’s value range.

The algorithm is repeated until the difference between the minimum and maximum values of each parameter drops below 1%, or until a total number of repeats (N_R = 6) is performed.

Methods

Simulation Methods

Numerical simulations were used to investigate the accuracy and precision in fitting the three-pool model over a range of experimental conditions. We also compared the results of the three-pool model to results derived using the two-pool mode.

Theoretical data were calculated using Eqns. [9] and [10] for F_F ={0, 0.10, 0.20, 0.30, 0.40 and 0.50}; for M_F = {0.05, 0.1, 0.15, 0.2 and 0.25}. This provided a 6×5 F_F vs. M_F grid. T_1,M, T_1,IE, T_1,F, T_2,M, T_2,IE, T_2,F, and τ_M were held constant at 465ms, 965ms, 3500ms, 12ms, 90ms, 250ms, and 125ms, respectively (1, 10, 11).

For each simulation, 50,000 realizations were calculated from theoretical data with Gaussian-distributed additive noise. The two and three-pool models were fit to the simulated data, with the accuracy (absolute percent difference between the known and estimated values) and precision (mean divided by the standard deviation) of the M_F estimates evaluated and compared.

In Vivo Data Acquisition

To evaluate in vivo performance, CNS data were acquired across a broad range of participants representing a mix of healthy and pathological conditions. Data were acquired of healthy 3 month old male infant; a healthy 24 year-old adult male; and an 81 male AD patient (mini-mental state exam score = 18). Cervical spine data were acquired of a 30 year-old female MS patient. To provide insight into the method’s reproducibility, data were acquired of the 24 year-old adult male on 5 separate occasions spanning 5 weeks. To inform on inter-subject variability, data were acquired of 10 1-year old infants (353-383 days of age, 7 female).

All scanning was performed following informed consent and with IRB approval from the host institution. Data were acquired on a Siemens Tim Trio scanner with a 12-channel head and neck RF array or spine array and the following acquisition parameters.

Infant Brain Acquisition Strategy

Whole-brain sagittal orientation with a 16cm² × 15cm field of view (FOV) and 96 × 96 × 88 acquisition matrix. SPGR: TE/TR = 5.5 ms / 13 ms; flip angles = (2, 3, 4, 5, 6, 7, 10 and 14)°; receiver bandwidth (BW) = 350 Hz/voxel bSSFP: TE/TR = 5.3 ms / 10.5 ms; flip angles = (11, 16, 19, 23, 27, 35, 50 and 70)°; BW = 350 Hz/voxel. Reduced resolution (half-size in each phase-encode direction) inversion-prepared (IR-) SPGR images were also acquired matched with the SPGR parameters and inversion delays of 50ms and 850ms to help correct for flip angle errors (9). The bSSFP data were acquired with two RF phase-cycling patterns (0 and 180°) to correct for B₀ inhomogeneity (9).

Adult Brain Acquisition Strategy

Whole-brain sagittal orientation with a 22cm² × 17cm FOV and 128 × 128 × 98 acquisition matrix. SPGR: TE/TR = 2.4 ms / 5.4 ms; flip angles = (3, 4, 5, 6, 7, 9, 13 and 18)°; BW = 380 Hz/voxel bSSFP: TE/TR = 2.2 ms / 4.4 ms; flip angles = (10, 13, 17, 20, 23, 30, 43, and 60)°; BW = 560 Hz/voxel. A reduced resolution inversion-prepared (IR-) SPGR image was also acquired with an inversion delay of 450ms, and the bSSFP data were acquired with 0 and 180 degree RF phase-cycling patterns.

Adult Spine Acquisition Strategy

Whole cervical-spine sagittal orientation with a 20cm² × 15cm FOV and 112 × 224 × 128 acquisition matrix. SPGR: TE/TR = 2.7 ms / 6.1 ms; 8 linearly spaced flip angles between 1 and 18°; BW = 400 Hz/voxel bSSFP: TE/TR = 2.3 ms / 4.6 ms; 8 linearly spaced flip angles between 5 and 45°; BW = 600 Hz/voxel. A reduced resolution inversion-prepared (IR-) SPGR image was also acquired with an inversion delay of 750ms, and the bSSFP data were acquired with 0 and 180 degree RF phase-cycling patterns.

Following acquisition, the individual flip angles images for each participant were linearly aligned to account for subtle intra-scan motion; non brain or spine signal was removed from each image, and the two and three-pool models fit voxel-wise to the data.

To compare the models, the two-pool M_F map was subtracted from the corresponding three-pool M_F map. It was expected that differences would be found bordering the ventricles and sulci, with no difference shown in the white and grey matter.

To examine the in vivo inter-scan reproducibility of the method, 5 sets of healthy adult repeat data were linearly aligned and voxel-wise measures of the coefficient of variation (CoV) of the M_F maps were calculated. Likewise, inter-subject variability was evaluated by calculating voxel-wise CoV measures across 10 healthy 1 year old infants.

Results

Simulation Results

Figure 1 displays the myelin water fraction sub-component of the simulation results exploring the performance of the two and three-component models across the range of M_F and F_F values. As might have been expected, as the free-water compartment size (F_F) was increased, the two-pool M_F value became increasingly under-estimated. In a further attempt to accommodate the additional water pool, the IE water T₁ and myelin water residence time values were increasing over-estimated as F_F increased (not shown). In contrast, as hoped, the 3-pool model accommodates the increasing free water fraction well, with no M_F under-estimation or IE water T₁ over-estimation observed. Both models were found to provide comparable myelin water T₁ and T₂ values. Accuracy of the three-pool MWF values was also found to be high across the experimental conditions examined, with less than 10% error noted.

Figure 1.

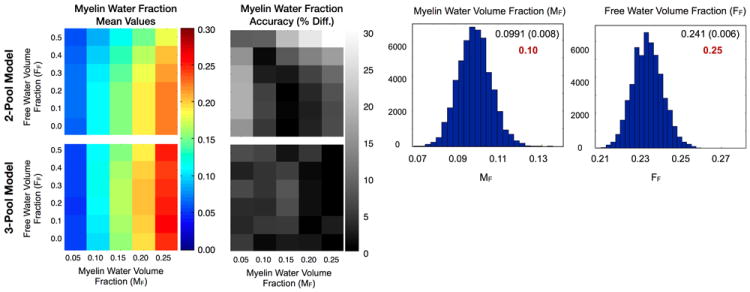
Results from the numerical simulation comparing the 2 and 3-pool model myelin water fraction value accuracy over and range of myelin and free water fractions.

To shed light on the uniqueness of solution found, Figure 1 also contains histograms showing the distribution of the fitted myelin water and free water fraction parameters for the 50,000 simulation realizations for the case of M_F = 0.1 and F_F = 0.20. If the algorithm converged non-uniquely, we would expect to see multiple peaks within these parameter histograms, or in the worse case, a uniform distribution. The results show Gaussian distributions for each parameter, centered about the ‘true’ value, suggesting the algorithm is converging to the same solution repeatedly. Mean and standard deviation values are given for each parameter, with the ‘true’ value also given in red type. While not shown, the histogram results for the other fitted parameters were also Gaussian shaped with mean, standard deviation and true values of: T_1,M = (460ms, 13ms, 465ms), T_1,IE = (979ms, 18ms, 965ms), T_1,F = (3527ms, 150ms, 3500ms), T_2,M = (11.6ms, 0.52ms, 12ms), T_2,IE = (90ms, 2.4ms, 90ms), T_2,F = (262ms, 26ms, 250ms) and τ_M = (126ms, 28ms, 125ms).

In Vivo Data Results

In vivo data results are shown in Figs. 2 and 3. Figure 2 contains a comparison of the 2 and 3-pool model derived M_F maps, alongside reference anatomical images and the 3-pool free water fraction (F_F) maps the healthy infant and healthy adult, as well as the MS and AD patient. Differences between the 2 and 3-pool M_F is most readily visualized in the difference (3-pool minus 2-pool result) map. For each participant, the difference between the two models is most apparent in partial volume voxels - those bordering the ventricles and meninges in the brain, and along the surface of the spinal cord. In these areas, the 2-pool model under-estimates the myelin volume fraction as predicted by the numerical simulations (Fig. 1). This effect is particularly evident in the AD patient data, where regions of the caudate nucleus and forceps major do not appear in the 2-pool M_F map. These areas are, however, visible in the 3-pool map.

Figure 2.

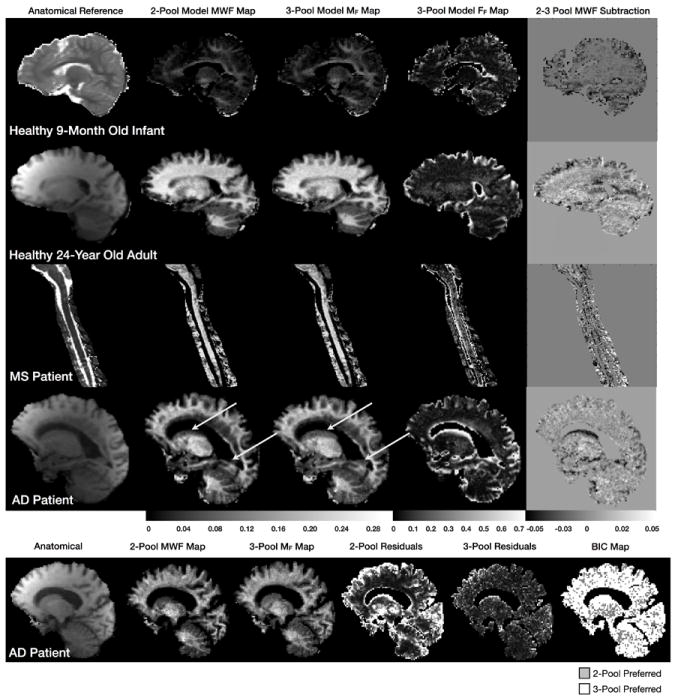
Two and three-pool model derived myelin water fraction maps for the 9 month old infant, 24 year old adult, and MS and AD patients. Shown for each are corresponding reference anatomical, the calculated free water volume fraction map, and a myelin water fraction difference map calculated by subtracting the three-pool MWF map from the two-pool result.

Figure 3.

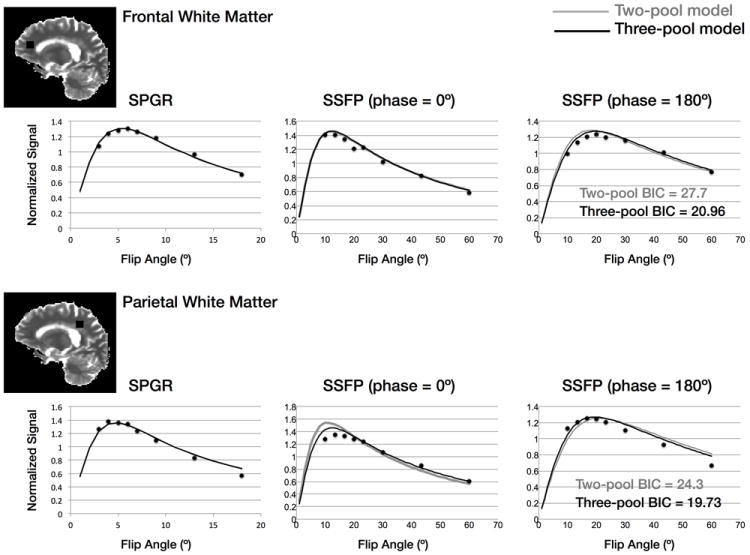
Example raw data and reconstructed two and three-pool signal curves for two different brain regions. The two-pool model is shown by the grey line, the three-pool model by the dark line. The BIC metrics calculated for both cases show the three-pool model to be preferred.

Within more homogeneous white and grey matter, the two models provide comparable results. We calculated a M_F difference of less than 0.01 (3%) in white matter. This result is also consistent with the numerical simulations (Fig. 1). Model preference is quantified in the final panel of Fig. 2, which compares the two and three-pool model fit residuals for the AD patient, as well as results of a model selection approach using the bayesian information criterion (BIC, 16), which shows the 3-pool model to be justified over the majority of brain voxels. Further exploration of this is shown in Fig. 3, which shows raw data vs. flip angle curves for two different brain regions of interest (obtained from the older AD patient) and reconstructed 2-pool and 3-pool model curves. Though subtle, differences are apparent between the 2 models. Calculated BIC metrics are shown on each curve, showing the 3-pool model to be preferred in both cases.

Figure 4 shows results of the single-subject (24 year old adult male scanned 5 times) repeatability (a) and multi-subject (10 1 year old infants) inter-subject reproducibilities (b) studies. Also shown in Fig. 4 is the result of an additional study of fitting algorithm stability. The stochastic nature of the fitting method is a potential source of error in mcDESPOT. To better understand this potential source of error, the fitting was repeated on the same data 500 times and the CoV of the estimates calculated. A slice through this CoV map is shown in Fig. 4c.

Figure 4.

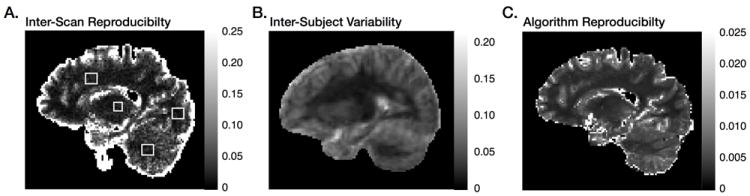
Results from the (a) intra-scan; (b) inter-subject variability; and (c) algorithm reproducibility studies. Shown for each are maps of the coefficient of variation calculated from repeated measures. Outline boxes in (a) denote regions of interest used to determine the mean CoV (Table 1). For the inter-scan reproducibility, a mean CoV of 0.059 was calculated. Inter-subject variability was found to be 0.1 1; and for the algorithm reproducibility, a mean CoV of 0.09 was found.

A slice through the inter-scan CoV map is shown in Fig. 4a, with average CoV measures obtained from 4 brain regions (frontal, occipital and cerebellar white matter, and thalamus) are noted in Table 1. The weighted average CoV across all four regions was 0.059.

Table 1.

Mean inter-scan and inter-subject MWF coefficient of variation values obtained from the frontal, occipital and cerebellar white matter, and the thalamus. Regions are depicted in Fig. 4a.

Brain Region	Inter-Scan CoV	Inter-Subject CoV
Frontal White Matter	0.061	0.107
Occipital White Matter	0.051	0.093
Cerebellar White Matter	0.064	0.112
Thalamus	0.058	0.126
Average	0.059	0.109

Results of the algorithmic stability analysis are shown in Fig. 4c. The CoV, averaged over the whole slice was 0.0094, indicating the algorithm converges similarly despite it’s random nature. This is an important result, showing not only stability of the algorithm, but also of the model itself. A potential issue encountered in fitting complex models is the occurrence of local minima: multiple parameter sets providing similar curves and model residuals. If this were true of the 3-pool model used herein, we would have expected to see low reproducibility in Fig. 4c, reflecting essentially random results from each solution iteration. The high reproducibility noted suggests the fitting algorithm consistently converges to the same unique solution, as was previously shown in the simulation results (Fig. 1) Improved reproducibility might be achieved through increasing the number of iterations of the algorithm, or increasing the number of samples taken at each iteration. Both, however, would increase computation time, currently ~14 hours (on an 8-core Intel I7 2.66GHz MacPro).

Discussion and Conclusions

Reliable estimation of myelin content has inherent interest in the study of de and dys-myelinating disorders, as well as neurodevelopmental or psychiatric disorders that may be associated with aberrant brain connectivity.

mcDESPOT is a potentially rapid and whole-brain quantitative MCR technique that may offer new opportunities for investigating the etiology and pathology of these disorders as well as normative development (17). However, to be of clinical or diagnostic utility, the method must provide robust results that adequately characterize the underlying tissue. Many disorders, including MS and AD, are associated with marked brain atrophy and gross anatomical lesions beyond focal or widespread myelin alteration. These pathological hallmarks may confound the interpretation of mcDESPOT results as the conventional two-pool mcDESPOT model approach may under-estimate the myelin water fraction in regions containing mixtures of brain tissue and free or bulk water, leading to the erroneous interpretation of advanced pathology, or in the ‘staging’ of the disease course.

In an effort to account for this, we have included an additional non-exchanging water pool to the model, and have evaluated this expanded approach through numerical simulations and in vivo imaging data.

Within homogeneous white and grey matter, results show the 3-pool models deviates negligibly (less than 3%) from the 2-pool model. This small difference may reflect reduced accuracy owing to the increased number of free parameters that must be fit in the expanded model. Alternatively, this difference may be anatomically relevant, possibly (though unlikely) reflecting a vascular compartment. As the bulk water pool fraction increases, numerical simulations show an increasing under-estimation of the myelin water fraction. This is visualized in vivo within boundary voxels between grey matter or spinal cord and CSF spaces. The 3-pool model effectively recovers this under-estimation, as most easily observed within the AD patient data. Examination of the BIC map for this patient shows that in these areas the 3-pool model is justified by the data.

A potential limitation of the model proposed herein is that of no exchange between the ‘tissue’ water and the free bulk water. This assumption is likely justified within the ventricles and meninges, since water must cross the blood-brain barrier. However, no such barrier exists in the case of edema, corresponding to pathologies such as black holes or white matter hyperintensities. Omission of free water exchange may result in a systematic bias in the calculated free water fraction. This may explain the non-zero free water component found within the homogeneous white matter in the in vivo data. Inclusion of exchange significantly muddles both the model and analysis, as it must first be determined which water pool(s) the free water may exchange with (likely only the IE water pool). Beyond modeling complications, this will also introduce two additional free-parameters to the model, which significantly complicates fitting.

This paper has aimed to investigate the effect of including an additional free-parameter into the mcDESPOT framework, and to evaluate the ability to reliably and robustly solve the resultant nine parameter model using clinically acquired in vivo data. What remains unaddressed is the accuracy of this model. Unfortunately, addressing this issue is not straightforward. Phantoms, such as dairy cream, provide multiple relaxation species but have the additional confound of different resonant frequencies associated with each species. ‘Wedge’ phantoms containing different materials with different relaxation properties may also be used, but obtaining accurate information regarding exchange between the differing materials is difficult. One could consider more exotic phantoms, in which the relaxation parameters could be adjusted with gadolinium and exchange rates via temperature or pH. However, if one is predominantly concerned with estimates of myelin water fraction, at the expense of the other metrics, comparison with histology will provide the surest validation.

An important consideration in any quantitative imaging technique is its inter-scan repeatability and inter-subject variability, as both inform on sample sizes required for clinical studies as well as predictive power. In this work, the 3-pool results are shown to have high inter-scan reproducibility, with a average CoV of 5.9%. This is of particular importance to longitudinal studies of disease progression or treatment efficacy. Inter-subject variability was also shown to be low, with a mean CoV of 0.109. Further studies incorporating additional male and female participants will be required to definitely state the reproducibility of the approach. Of note, however, these results (and those of the numerical simulations) contradict a recent theoretical analysis of mcDESPOT precision (18). It is possible the difference in analysis approach (unconstrained in the theoretical analysis, vs. constrained here) is the reason behind the high precision observed here compared with predicted. We have evaluated the model over a range of pathological conditions and age-ranges and have not noticed a degradation in results.

Overall, we find that the 3-pool model agrees well with the conventional 2-pool approach in homogeneous tissue whilst improving the performance of the method in areas of partial volume. In light is this finding, we conclude that it is the preferred choice for future analysis.

Appendix A

The two-component models of the equilibrium SPGR and bSSFP magnetizations are given by Eqns. [1] and [2], respectively. For the SPGR model, only the longitudinal magnetization needs to be considered if ideal spoiling is assumed for the transverse magnetization. Under these conditions,

$$M_{\mathit{SPGR}}=\rho {\left[\begin{array}{cc}{M}_F& {\mathit{IE}}_F\end{array}\right]}^T$$ [A1]

and

$$A_{\mathit{SPGR}}=\left[\begin{array}{cc}-\frac{1}{T_{1,M}}-k_{M\to \mathit{IE}}& k_{\mathit{IE}\to M}\\ k_{M\to \mathit{IE}}& -\frac{1}{T_{1,\mathit{IE}}}-k_{\mathit{IE}\to M}\end{array}\right].$$ [A2]

In the case of bSSFP, both the longitudinal and transverse magnetization components need to be considered, as both are driven to dynamic equilibrium. Under these conditions,

$$A_{\mathit{bSSFP}}=\left[\begin{array}{cccccc}-\frac{1}{T_{2,M}}-k_{M\to \mathit{IE}}& k_{\mathit{IE}\to M}& \mathrm{\Delta }{\omega }_M& 0& 0& 0\\ k_{M\to \mathit{IE}}& -\frac{1}{T_{2,\mathit{IE}}}-k_{\mathit{IE}\to M}& 0& \mathrm{\Delta }{\omega }_{\mathit{IE}}& 0& 0\\ -\mathrm{\Delta }{\omega }_M& 0& -\frac{1}{T_{2,M}}-k_{M\to \mathit{IE}}& k_{M\to \mathit{IE}}& 0& 0\\ 0& -\mathrm{\Delta }{\omega }_{\mathit{IE}}& k_{M\to \mathit{IE}}& -\frac{1}{T_{2,\mathit{IE}}}-k_{\mathit{IE}\to M}& 0& 0\\ 0& 0& 0& 0& -\frac{1}{T_{1,M}}-k_{M\to \mathit{IE}}& k_{M\to \mathit{IE}}\\ 0& 0& 0& 0& k_{M\to \mathit{IE}}& -\frac{1}{T_{1,\mathit{IE}}}-k_{\mathit{IE}\to M}\end{array}\right]$$ [A3]

and

$$C=\rho {\left[\begin{array}{cccccc}0& 0& 0& 0& \frac{M_F}{T_{1,M}}& \frac{{\mathit{IE}}_F}{T_{1,\mathit{IE}}}\end{array}\right]}^T.$$ [A4]

In the above expressions, k_M→IE is the exchange rate from the myelin-associated to the intra/extra-cellular water pools; k_IE→M is the exchange rate from the intra/extra-cellular to the myelin-associated water pools; Δω_M and Δω_IE are the off-resonance values (with respect to the central water peak); and ρ is a term proportional to the equilibrium longitudinal magnetization. Assuming the close proximity of the water pools, we assume that Δω = Δω_M = Δω_IE.

Appendix B

To account for an addition third water component in the SPGR and bSSFP models, the M_SPGR, A_SPGR, A_bSSFP, and C matrices (Eqns. [A1] through [A4]) are expanded as

$$M_{\mathit{SPGR}}=\rho {\left[\begin{array}{ccc}{M}_F& {\mathit{IE}}_F& 1-(M_F+{\mathit{IE}}_F)\end{array}\right]}^T,$$ [B1]

$$A_{\mathit{SPGR}}=\left[\begin{array}{ccc}-\frac{1}{T_{1,M}}-k_{M\to \mathit{IE}}& k_{IE\to M}& 0\\ k_{M\to \mathit{IE}}& -\frac{1}{T_{1,\mathit{IE}}}-k_{\mathit{IE}\to M}& 0\\ 0& 0& -\frac{1}{T_{1,F}}\end{array}\right],$$ [B2]

$$C=\rho {\left[\begin{array}{ccccccccc}0& 0& 0& 0& 0& 0& \frac{M_F}{T_{1,M}}& \frac{{\mathit{IE}}_F}{T_{1,\mathit{IE}}}& \frac{F_F}{T_{1,F}}\end{array}\right]}^T,$$ [B3]

and

$$A_{\mathit{bSSFP}}=\left[\begin{array}{ccccccccc}-\frac{1}{T_{2,M}}-k_{M\to \mathit{IE}}& k_{\mathit{IE}\to M}& 0& \mathrm{\Delta }\omega & 0& 0& 0& 0& 0\\ k_{M\to \mathit{IE}}& -\frac{1}{T_{2,\mathit{IE}}}-k_{\mathit{IE}\to M}& 0& 0& \mathrm{\Delta }\omega & 0& 0& 0& 0\\ 0& 0& -\frac{1}{T_{2,F}}& 0& 0& \mathrm{\Delta }\omega & 0& 0& 0\\ -\mathrm{\Delta }\omega & 0& 0& -\frac{1}{T_{2,M}}-k_{M\to \mathit{IE}}& k_{\mathit{IE}\to M}& 0& 0& 0& 0\\ & -\mathrm{\Delta }\omega & 0& k_{M\to \mathit{IE}}& -\frac{1}{T_{2,\mathit{IE}}}-k_{\mathit{IE}\to M}& 0& 0& 0& 0\\ & & -\mathrm{\Delta }\omega & 0& 0& -\frac{1}{T_{2,F}}& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& -\frac{1}{T_{1,M}}-k_{M\to \mathit{IE}}& k_{\mathit{IE}\to M}& 0\\ 0& 0& 0& 0& 0& 0& k_{M\to \mathit{IE}}& -\frac{1}{T_{1,\mathit{IE}}}-k_{\mathit{IE}\to M}& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& -\frac{1}{T_{1,F}}\end{array}\right]$$ [B4]