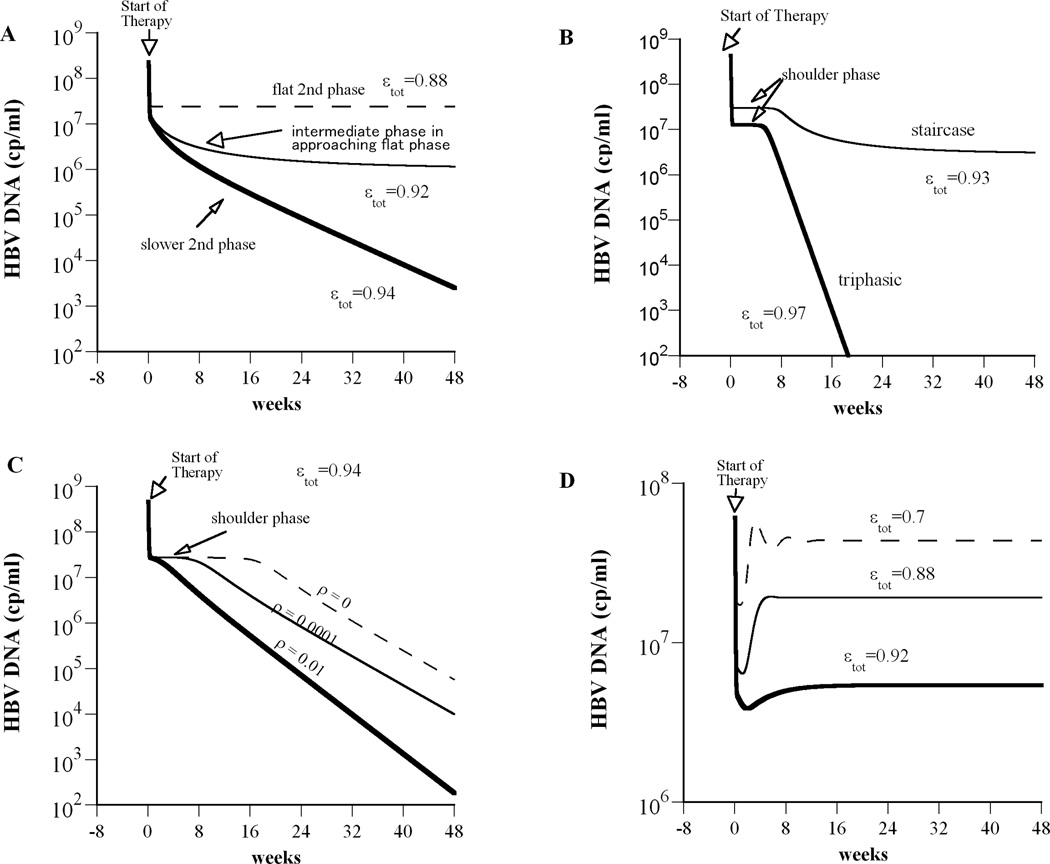
Figure 2.

Model simulations predict complex HBV DNA decline profiles during drug therapy. We solved our model (Eq. 1) numerically using Berkeley-Madonna (version 7.0.2; http://www.berkeleymadonna.com). (A) A flat second phase occurs when ε_tot<ε_c (dashed line; here ε_tot=0.88; ε_c=0.934). When ε_tot is close to ε_c (but still ε_tot < ε_c), then after the rapid viral decay phase an intermediate slower phase is predicted that approaches a flat final phase (thin solid line; ε_tot=0.92). When ε_tot > ε_c we obtain a biphasic viral decline (thick line; ε_tot=0.94). (B) If we decrease the ratio of the target cell to the infected cell replication rate from r_T/r_I = 8.5 (used in (A)) to r_T/r_I= 2, a shoulder phase emerges. Staircase and triphasic viral decay profiles are represented by thin and thick solid lines, respectively. For the staircase profile total drug efficacy, ε_tot=0.93, is lower than the critical drug efficacy, ε_c=0.934 and therefore after the third phase of viral decay the viral load stabilizes in a steady state until end of treatment. For the triphasic profile ε_tot> ε_c (ε_tot=0.97) and thus viral will continue to decline under therapy. (C) If we increase the rate constant for cure of infected cells, ρ, from 0 (i.e., no cure) to 0.01 day⁻¹, the shoulder phase of the triphasic decline disappears and we obtain a biphasic viral decline. Here ε_tot=0.94 and r_T/r_I = 1.25. (D) Viral rebound during treatment occurs when the hepatocyte replication rate is low, r_T=0.51 day⁻¹, r_T/r_I = 2 and ε_tot< ε_c (η=0). Except as noted, model parameters used were: T_max = 1.9×10⁷ cells ml⁻¹, d_T = 0.004 day⁻¹, p = 92.3 virions cell⁻¹ day⁻¹, β= 7.1×10⁻⁹ ml day⁻¹ virions⁻¹, c = 3.5 day⁻¹, δ= 0.25 day⁻¹, ρ=0 day⁻¹, r_T= 3.0 day⁻¹, r_T/r_I = 8.5, η=0.5 and s= 1 cell ml⁻¹ day⁻¹.