The Regional Healthcare Ecosystem Analyst (RHEA): a simulation modeling tool to assist infectious disease control in a health system

Abstract

Objective

As healthcare systems continue to expand and interconnect with each other through patient sharing, administrators, policy makers, infection control specialists, and other decision makers may have to take account of the entire healthcare ‘ecosystem’ in infection control.

Materials and methods

We developed a software tool, the Regional Healthcare Ecosystem Analyst (RHEA), that can accept user-inputted data to rapidly create a detailed agent-based simulation model (ABM) of the healthcare ecosystem (ie, all healthcare facilities, their adjoining community, and patient flow among the facilities) of any region to better understand the spread and control of infectious diseases.

Results

To demonstrate RHEA's capabilities, we fed extensive data from Orange County, California, USA, into RHEA to create an ABM of a healthcare ecosystem and simulate the spread and control of methicillin-resistant Staphylococcus aureus. Various experiments explored the effects of changing different parameters (eg, degree of transmission, length of stay, and bed capacity).

Discussion

Our model emphasizes how individual healthcare facilities are components of integrated and dynamic networks connected via patient movement and how occurrences in one healthcare facility may affect many other healthcare facilities.

Conclusions

A decision maker can utilize RHEA to generate a detailed ABM of any healthcare system of interest, which in turn can serve as a virtual laboratory to test different policies and interventions.

Introduction

As healthcare systems continue to expand and interconnect with each other through patient sharing, healthcare facility administrators, policy makers, infection control specialists, and other decision makers have to take account of the entire healthcare ‘ecosystem’ when seeking to prevent and control infectious diseases. Individual healthcare facilities are rarely isolated entities but rather are connected to other healthcare facilities and the community through extensive patient sharing, thus forming a dynamic ecosystem.^{1 2} Patients discharged from one facility may immediately or after an intervening stay in the community, move to another facility carrying infectious diseases with them.

Creating models de novo of large healthcare systems or of all the healthcare facilities in a region can require substantial effort and time. To make this task easier, we developed a computational software tool, the Regional Healthcare Ecosystem Analyst (RHEA) which decision makers can use to rapidly create a detailed agent-based simulation model (ABM) of any healthcare system or set of healthcare facilities in any sized region with integrated infectious disease transmission models. The resulting simulation model can serve as a virtual laboratory to help decision makers (eg, public health officials, hospital administrators, and infection control specialists) test different policies, strategies, and interventions before actually implementing them, thereby saving the time and effort that trial and error would incur. This study introduces RHEA and its features, using a sample location (Orange County, California, USA) and a sample infectious pathogen (methicillin-resistant Staphylococcus aureus (MRSA)) to demonstrate the importance and impact of RHEA's features.

Materials and methods

The Regional Healthcare Ecosystem Analyst

We developed an initial version of RHEA in Fortran 90 and a subsequent version in C++. The user can feed data (entered into standard spreadsheet templates that are then read into RHEA) on a healthcare system of any size or configuration into a standard input deck which RHEA can then use to rapidly create an ABM of that system. Table 1 summarizes the inputs that may be needed for RHEA to build a model and the potential data sources for these inputs. The detail of the RHEA-generated ABM will correspond to the detail of the input data.

Table 1.

Summary of RHEA inputs and potential data sources

Parameter	Potential data sources
Facility characteristics
Admissions, bed size, length-of-stay distribution*, age, gender, insurance, case mix	National and state hospital databases3 4
Number and types of wards, beds per ward, patient volume per ward	Facility surveys
Patient transfer data, by facility	National and state hospital databases3 4
Pre-admission and post-discharge facility locations	National long-term care databases5
Probability of admission to an ICU versus general ward	Facility surveys
Probability of death, by facility	National and state databases
Probability of readmission, by facility	National and state hospital databases
Readmission to same facility	National long-term care databases
Readmission to another facility
Time to readmission (distribution)	National and state hospital databases
	National long-term care databases
Transmission coefficient (β)†	Literature
	Facility surveys
Infectious disease states and characteristics‡	Literature
	Facility surveys
Infectious disease prevalence or incidence	Literature
	Facility surveys

*Can be stratified to represent different disease states or types of patients (eg, ICU or general ward).

†Can be computed from the reproductive rate (R) and disease characteristics.

‡Including: incubation period, duration of infectiousness, duration of illness, duration of recovered/immune state, etc, for state countdown clocks.

ICU, intensive care unit; RHEA, the Regional Healthcare Ecosystem Analyst.

Computational agents representing patients

In the generated ABM, a computational agent represents each patient. Like a real patient, each simulated agent has a set of parameters, each mapping to a particular characteristic, such as gender, age, race/ethnicity, socioeconomic status, insurance status, presence/absence of a variety of co-morbidities, and infectious disease status. Each parameter can assume a set of user-specified appropriate categorical, ordinal, or continuous values (eg, infectious disease status, where 0 means the agent is susceptible, 1 means colonized, and 2 means colonized with active infection; or location, where each facility, ward, and bed within the ward has a unique identifier). As described below, some of the behaviors, movements, and actions of each agent are conditional on the agent's various parameter values.

Representations of healthcare facilities

RHEA can create a model with practically any number and type of healthcare facilities. Each facility has an identification parameter (eg, if a model has 100 facilities, each facility has a unique identification number from 1 to 100). Each virtual facility has a set of parameters that mirror a real healthcare facility's characteristics (facility type (acute care, long-term acute care (LTAC), and long-term care), total number of beds, and patient length-of-stay (LOS) distribution). In each facility, the beds are divided into intensive care units (ICUs) and/or general wards (eg, an acute care hospital may have a few ICUs and many general wards, while a nursing home may have a single ward). The user can specify the number of beds in each ward/unit.

Agent (patient) movement

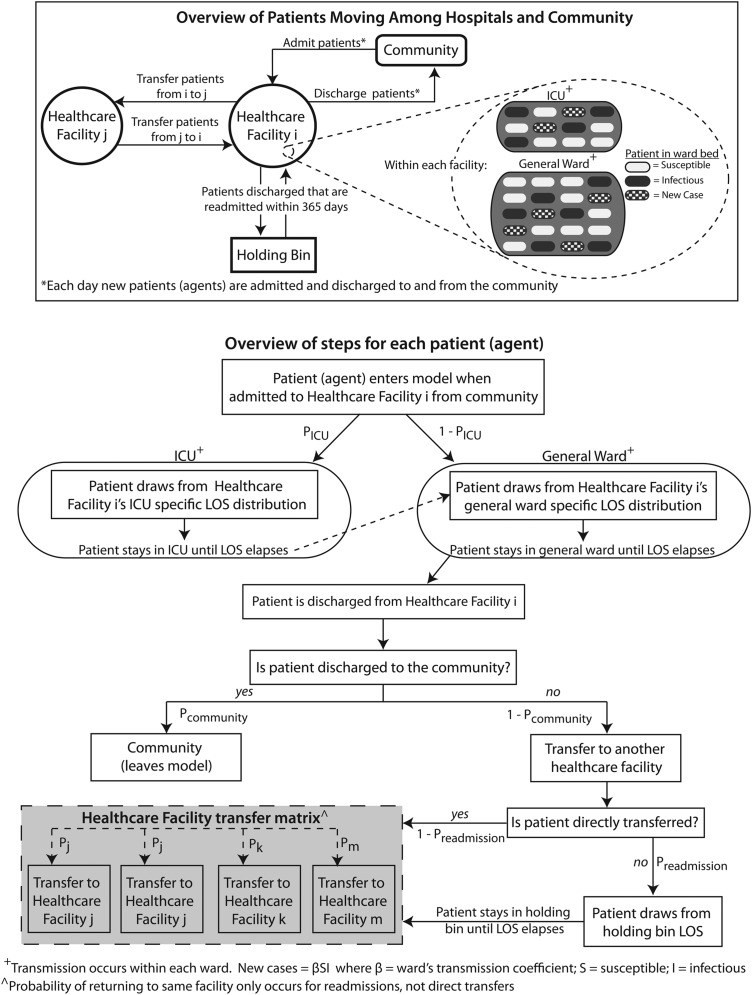
Figure 1 shows how agents flow through a RHEA-generated model. The simulation proceeds in 1-day discrete time steps. Each simulated day, agents (representing admissions) enter each healthcare facility and fill its available beds. On admission, the agent draws from that facility's LOS distribution (specified by the user) which sets the starting value for that agent's facility LOS countdown clock, which determines how many days the agent stays in that facility (eg, one agent may have its facility LOS countdown clock set initially at 2 days, while another may have it set at 5 days). Each passing day decreases the agent's facility LOS countdown clock by 1 day until it reaches zero, prompting the agent to leave the facility.

Figure 1.

Regional Healthcare Ecosystem Analyst overview. ICU, intensive care unit; LOS, length of stay.

If a facility has more than one type of unit/ward, a probability draw determines what type of unit/ward the agent enters (eg, if the randomly drawn probability between 0 and 1 is less than the user specified probability of entering an ICU versus other wards (p_ICU), the agent attempts to enter an ICU; otherwise, the agent enters a general ward). Then, a subroutine scans the facility's complement of empty beds. Each empty bed has an equal probability of being filled by the agent. If all beds are filled, the agent will have to move to another facility (see below on how the destination of discharged agents is governed).

If an agent moves into an ICU, the agent draws from that facility's ICU-specific LOS distribution (user-specified) which sets the starting value for the agent's ICU LOS countdown clock that determines how many days the agent stays in that ICU. As with the agent's facility LOS countdown clock, each passing day decreases the agent's ICU LOS countdown clock by 1 day until it reaches zero, prompting the agent to leave the ICU. The agent's facility LOS countdown clock decreases simultaneously. If upon transfer from the ICU, the agent's facility LOS countdown clock is still greater than zero, the agent moves into the general ward and remains there until that agent's facility LOS countdown clock reaches zero at which time the agent leaves the facility. If the facility LOS countdown clock has already reached zero when the agent's ICU LOS countdown clock hits zero, the agent moves to the general ward for 1 day before leaving the facility.

The user can specify whether the facility LOS distribution or ICU LOS distribution is the same for all agents or conditional on a given agent characteristic. For example, the user has the option to dictate that agents infected by a pathogen will draw from a different (eg, longer) LOS distribution (if such a LOS distribution is available).

Upon discharge, another subroutine determines the agent's destination. A probability draw between 0 and 1 determines whether an agent moves to the community and leaves the model (eg, a draw of less than a user-specified p_community means the patient moves directly to the community). Otherwise the agent moves to another facility, either immediately (direct transfer) or after an intervening stay in the community (readmission). Each agent moving to another facility has a probability of ending up in any of the other facilities (eg, a patient being transferred from facility 1 may have a 10% probability of going to facility 2, a 15% probability of going to facility 3, etc). An agent's p_community may depend on the agent's characteristics (eg, agents infected by a pathogen may be more likely to move to another facility than to return to the community). At each time step, each agent can have a probability of death and thereby leave the model. (Since our current study aims to demonstrate the other general features of the model, mortality was set at zero.)

A probability draw determines whether a direct transfer or readmission occurs (p_readmission; and thereby entering a holding bin). Each agent entering the holding bin draws from a facility-specific days-to-readmission distribution (lognormal) that determines how many days the agent stays until readmission. Once this assigned days-to-readmission elapses, the agent has different probabilities of being admitted to any of the healthcare facilities in the region.

Infectious disease states

Each day an agent can assume one of a finite set of mutually exclusive infectious disease states, as specified by the user (eg, for MRSA, the user may specify that the agent can assume two (non-colonized or colonized), three (non-colonized, colonized, and active infection), or more states. For influenza, an agent may have four possible states: susceptible (able to be infected), exposed (infected but not yet able to transmit the pathogen to others), infectious (able to transmit to others), or resistant (unable to be infected). Each state has a countdown clock, which can be turned off (an agent remains in that state indefinitely) or on (an agent remains in that state for a finite length of time) and dictates the number of days the agent remains in that state. When turned on, the agent's state countdown clock starts at a certain number of days (drawn from a user-specified distribution) and then decreases by one with each passing day; when the clock reaches zero, the agent transitions to the next state in the progression.

Infectious disease transmission

Infectious disease transmission occurs within each ward/unit via the following subroutine. Each day in each ward/unit, a subroutine counts the number of agents that are in an actively infectious state and the number of susceptible agents and then utilizes the following equation to calculate the number of new cases that should appear in that ward/unit for that day:

New cases for that day in that ward/unit=(ward/unit specific transmission coefficient×number of agents in a susceptible state that day×number of agents in an infectious state that day)

The result (rounded to the nearest integer) specifies how many new cases the subroutine needs to ‘convert.’ The subroutine will then randomly select this number of susceptible agents in the ward/unit and converts their state from susceptible to infectious (or exposed or colonized, depending on the type and number of states specified by the user). For instance, if the formula determines that two new cases need to occur in a ward/unit and there are eight susceptible agents in the ward/unit, the subroutine will randomly select two from among the eight.

RHEA has default values for the transmission coefficient (β) for each ward/unit drawn from the literature, but the user can change any of these values. The formula above aims to represent not only direct contact between agents in a ward but also indirect contact via healthcare workers and the environment (eg, equipment). Since the subroutine performs the counts and calculates the formula for each ward/unit, infectious agents cannot influence the states of agents in a different ward/unit, that is, transmission can only occur within a ward/unit and not across wards/units. The user can determine if and when a patient's LOS increases after the patient newly acquires a pathogen.

Outcome measures

Generating a simulation model makes it straightforward for the user to tabulate daily statistics from almost every process. RHEA tracks the daily number of agents in each state within each ward/unit, in each facility. This allows the calculation of any epidemiologic measure that is a composite of these counts (eg, prevalence and incidence).

Using RHEA to create a virtual laboratory of the hospital ecosystem of Orange County, California

In order to demonstrate the capabilities and features of RHEA and their relative importance, we utilized RHEA to generate a detailed ABM of all 29 adult hospitals in Orange County, California, USA, and conducted a suite of experiments varying the values of different model parameters to explore their effects on the spread of a sample infectious pathogen (MRSA) throughout the hospital ecosystem of Orange County (OC). The input parameters were derived from state and national databases under institutional review board (IRB) approval from the Regents of the University of California; the modeling, which used de-identified data, was IRB exempt.

The first step was feeding the facility characteristics (table 2) via spreadsheets into RHEA to generate virtual representations of each healthcare facility. The admissions, bed capacity, and LOS distributions came from the mandatory hospital discharge dataset maintained by the California Office of Statewide Health Planning and Development (OSHPD).³ In addition to facility characteristics such as admissions and bed capacity, the OSHPD dataset consists of line item information on each admission to and discharge from all hospitals including diagnoses (via International Classification of Diseases, Ninth Revision (ICD-9) codes), dates of admission and discharge, and patient location before and after admission. The combination of admission and discharge dates and ICD-9 codes allowed calculation of LOS distributions for all patients for each facility as well as for those with an MRSA diagnosis (an ICD-9 code of 041.11 (S aureus bacterial infection), 038.11 (S aureus septicemia), or 482.41 (S aureus pneumonia) paired with the V09.0 (antibiotic resistance) code) to generate different LOS distributions for patients who are MRSA positive.^6–9

Table 2.

Orange County, California hospital characteristics fed into RHEA to generate virtual representations of hospitals

	Hospital characteristics				Hospital-specific LOS distribution		MRSA-stratified LOS distribution		MRSA transmission coefficient (β)
	Adult patient admissions in 2006	Bed capacity	Mean patient LOS (days)	Median LOS (days)	General ward LOS*	ICU LOS*	General ward LOS for patients without MRSA*	General ward LOS for patients with MRSA*	General ward β	ICU β
Acute care hospital
A	7111	127	6.57	4	1.57 (0.69)	1.25 (0.87)	1.56 (0.69)	2.20 (0.59)	0.00046	0.0109
B	15058	255	6.20	4	1.55 (0.69)	1.84 (0.63)	1.53 (0.68)	2.30 (0.68)	0.00065	0.0053
C	4540	70	5.70	4	1.40 (0.71)	1.19 (0.89)	1.39 (0.70)	2.17 (0.84)	0.00065	0.0067
D	21488	297	5.05	4	1.40 (0.60)	1.99 (0.58)	1.39 (0.59)	1.96 (0.72)	0.00083	0.0069
E	9202	102	4.06	3	1.24 (0.53)	1.84 (0.63)	1.23 (0.51)	1.91 (0.62)	0.0011	0.011
F	2481	30	4.55	4	1.33 (0.59)	1.84 (0.63)	1.31 (0.59)	1.89 (0.61)	0.0012	–
G	6932	83	4.41	3	1.30 (0.53)	1.84 (0.63)	1.29 (0.54)	2.04 (0.53)	0.00070	0.0120
H	2366	42	6.59	4	1.59 (0.72)	0.91 (1.00)	1.58 (0.72)	2.03 (0.53)	0.00063	0.0107
I	14347	258	6.59	4	1.49 (0.80)	1.63 (0.72)	1.47 (0.80)	2.28 (0.43)	0.00053	0.0060
J	13755	205	5.45	4	1.47 (0.62)	1.63 (0.72)	1.45 (0.60)	2.31 (0.66)	0.00075	0.0064
K	14281	194	4.96	4	1.37 (0.62)	1.84 (0.63)	1.36 (0.62)	2.17 (0.60)	0.00084	0.0085
L	16095	227	5.17	4	1.38 (0.65)	1.42 (0.80)	1.37 (0.64)	2.22 (0.81)	0.00078	0.0076
M	4028	47	4.30	4	1.28 (0.58)	1.22 (0.88)	1.27 (0.57)	1.97 (0.63)	0.0013	0.024
N	6535	102	5.72	4	1.46 (0.72)	2.54 (0.38)	1.45 (0.72)	2.11 (0.60)	0.00062	0.0077
O	11375	168	5.41	4	1.39 (0.69)	1.84 (0.63)	1.38 (0.68)	2.31 (0.69)	0.00061	0.0048
P	4399	76	6.32	4	1.53 (0.64)	1.57 (0.74)	1.52 (0.63)	2.41 (0.90)	0.00047	0.0117
Q	12020	148	4.50	3	1.28 (0.61)	1.84 (0.63)	1.27 (0.61)	1.83 (0.69)	0.00096	0.0058
R	8951	139	5.67	4	1.46 (0.67)	1.34 (0.83)	1.45 (0.66)	2.15 (0.72)	0.00069	0.0088
S	11505	143	4.54	4	1.33 (0.55)	1.84 (0.63)	1.32 (0.54)	2.05 (0.58)	0.00093	0.0059
T	2773	52	6.94	5	1.62 (0.69)	1.84 (0.63)	1.62 (0.69)	1.62 (0.69)	0.00057	0.0105
U	15967	204	4.67	4	1.34 (0.58)	1.84 (0.63)	1.33 (0.57)	1.93 (0.66)	0.00090	0.0091
V	26292	364	5.06	4	1.40 (0.60)	1.84 (0.63)	1.39 (0.59)	2.07 (0.74)	0.00082	0.0072
W	4810	70	5.39	4	1.36 (0.67)	1.54 (0.75)	1.36 (0.67)	1.70 (0.57)	0.00093	0.0219
X	4881	71	5.38	4	1.41 (0.67)	2.11 (0.53)	1.41 (0.67)	1.98 (0.66)	0.00081	0.040
LTAC facility
AA	388	36	33.97	28.5	3.31 (0.70)	1.84 (0.63)	3.29 (0.71)	3.38 (0.64)	0.00033	–
BB	947	96	37.15	25	3.25 (0.86)	1.84 (0.63)	3.22 (0.86)	3.38 (0.64)	0.00028	–
CC	3082	79	9.38	5	1.73 (0.81)	1.84 (0.63)	1.72 (0.81)	2.37 (1.18)	0.0016	–
DD	966	33	12.47	11	2.41 (0.50)	1.84 (0.63)	2.41 (0.49)	2.50 (0.78)	0.0011	–
EE	1819	16	3.32	3	1.07 (0.46)	2.99 (0.26)	1.06 (0.45)	2.69 (0.43)	0.0056	–

*Mean (SD); lognormal length of stay.

ICU, intensive care unit; LOS, length of stay; LTAC, long-term acute care; MRSA, methicillin-resistant Staphylococcus aureus; RHEA, the Regional Healthcare Ecosystem Analyst.

The second step was to calibrate patient flow among the facilities and the communities by populating a transfer probability matrix spreadsheet that could be subsequently input into RHEA. This matrix consisted of rows representing each discharging hospital and columns representing each receiving hospital. A cell entry then is the probability of a patient discharged from the hospital for that row ending up in the hospital for that column. These probabilities are derived from the OSHPD dataset. Each person has a permanent unique encrypted identifier that remains fixed across all admissions, allowing patients to be tracked for 365 days as they move among facilities within the county.

Tracking patients after discharge also allowed us to calculate the time to readmission.

The third step was to calibrate the transmission model. Each ICU, general, and LTAC ward in the model had a specific β calibrated to achieve a 3%, 1%, or 2% incidence of new MRSA cases, respectively. These target incidences were based on real observed incidences of MRSA cases in the different ward/unit and facility types.^{10 11} By targeting these real-world incidences, β aims to account for differences in MRSA susceptibility among patients in different facilities and in transmission via staff members.

Validation of our RHEA-generated OC model entailed comparing the simulation output to empirical data when possible, by performing the following checks: verifying that the simulation-generated LOS distributions for each facility matched the empirical LOS data obtained from OSHPD; verifying that the simulated-generated distribution of delay times until readmission matched real-world data; and verifying that the hospital-to-hospital transfer counts generated during the simulation agreed with OSHPD data. When data were not available for direct comparison with the simulation output, we used expert judgment of the results within the broader context of epidemiology, the current literature, and knowledge of MRSA transmission. Validation of the model for other pathogens could be carried out in a similar manner.

Outcome measures for the study presented in this paper included MRSA prevalence and number of new MRSA cases over time in each healthcare facility. From these outcome measures, we calculated additional measures such as the absolute and relative changes in MRSA prevalence in each healthcare facility and county with different scenarios and parameters.

Results

The impact of transmission

Once RHEA generated an ABM of OC, a suite of experiments varied different model parameters to determine how they would affect MRSA prevalence in each healthcare facility. Each simulation run consists of running the model for 5112 simulated days for 100 000 Monte Carlo trials, allowing the outcome variables to reach steady state or 90% of their final value. Of the 5112 simulated days, the first 1460 days are a burn-in period until equilibrium is reached, after which an experiment can commence; these days are not used in the analysis. Reported results were averages (and distributions) of results from all 100 000 realizations.

Our first set of experiments evaluated how turning on and off transmission within the wards/units affected the spread of MRSA when all hospitals begin the simulation with a 5% MRSA prevalence. To establish the baseline, we turned transmission off (ie, β=0) in all hospitals, so that prevalence changes would be solely due to patient movement and simulated disease prevalence increases (ie, from 5% to 15%) in a single hospital. When this increase occurred in the largest hospital by bed capacity (hospital V), all other OC hospitals eventually experienced an MRSA prevalence increase. The median relative increase in other hospitals was 1.4% (range: 0.2–21.4%). This generated a median of 5.7 new cases a year in all other hospitals and a total of 2822 cases per year countywide. Simulating an MRSA outbreak in the hospital that sends and receives many patients from a large number of different hospitals over the course of a year (hospital I) led to a 2.0% median relative prevalence increase in all other hospitals (range: 0.3–6.0%). A hospital I outbreak generated a total of 1626 new cases a year in OC (median: 6.6 in each hospital). By contrast, a similar outbreak in an LTAC ward caused a >1% relative prevalence increase in only one other hospital.

Next, we repeated the suite of simulation runs after turning on the disease transmission feature in each ward/unit in each hospital. When the largest hospital (hospital V) experienced an increase in MRSA prevalence to 15%, disease prevalence in all other hospitals eventually increased by a median of 1.7% (range: 0.6–18.4%). This generated a median of 9.3 new cases (range: 0.4–25.0) in other hospitals for 3075 new cases countywide. Therefore, adding transmission further augmented the relative prevalence increase in other acute care hospitals by a median absolute difference of 0.3% (range: 0–0.8%). Although two LTACs actually experienced a lower (absolute difference of 3.0% and 1.6%) relative increase in prevalence when transmission was added, their absolute MRSA prevalence was higher with transmission (compared to no transmission).

Simulating an MRSA outbreak in hospital I led to a 2.6% median relative prevalence increase in all other hospitals (range: 0.7–6.2%), generating a median of 10.4 new cases a year in other hospitals (range: 1–28.6), for a total of 1871 cases annually countywide. Therefore, adding transmission further augmented the relative prevalence increase in other acute care hospitals by a median of 0.37% (range: 0–1.1%). Even with transmission, a similar outbreak in an LTAC caused a >1% relative prevalence increase in only one other hospital (generating only 35 new cases a year countywide).

When hospital V experienced a 50% increase in MRSA prevalence, there was a median 8.1% (range: 3.5–787.8%) relative increase countywide (≤79.4% change in all other hospitals). This outbreak generated 13 489 new MRSA cases a year in the entire county with a median of 43 cases in other hospitals. A 50% outbreak in hospital I caused a median 11.0% relative increase in the disease prevalence of all other hospitals (range: 3.3–26.7%), translating to a total of 8132 new cases annually countywide. A 50% MRSA increase in smaller hospitals and LTACs affected the prevalence in the county, although to a smaller extent (median: 0.2%; range: 0–711.5%).

All subsequent reported experiment results include disease transmission.

The impact of changes in lengths of stay

A second set of experiments kept initial MRSA prevalence at 5% in all hospitals and simply varied the LOS distribution for patients (from the same for all patients to one based on MRSA status). Making the LOS longer for those patients with the infectious disease (corresponding to the LOS for patients diagnosed with MRSA colonization as shown in table 2) increased MRSA prevalence (median relative change: 40.0%; range: 3.2–190.0%) throughout all facilities in OC. This corresponded to a median of 161 new cases a year (range: 1.7–755) in each hospital for a total of 6662 new cases per year countywide.

Changes in facility bed capacity

A third set of experiments explored the effects of varying hospital bed capacity, which proportionally scaled the number of admissions to the facility. Merely varying the bed capacity of hospital V (average bed capacity=364) affected MRSA prevalence throughout the county. Decreasing the bed capacity of this hospital by half (down to 182 beds) resulted in a 1.3% relative decrease in disease prevalence within this hospital and a 0.1% median relative decrease throughout the county. This change alone averted 20 new cases in hospital V and 34 new MRSA cases throughout the county annually. Conversely, doubling the bed capacity of the largest hospital to 728 beds resulted in a median 13.2% relative increase in MRSA prevalence in that hospital and a 0.3% relative increase in other hospitals across the county. This translated to 203 more cases in hospital V and 243 additional cases countywide per year.

Changes in probability of readmission

A fourth set of experiments altered the readmission probability for those patients with MRSA. Increasing the readmission probability for those with MRSA by 30% also increased MRSA colonization prevalence throughout the county. This increase in readmission probability caused a median 8.8% relative change in prevalence in all OC hospitals (range: 6.6–23.8%) and generated an additional 1192 cases a year countywide (median: 33; range: 4–105 per hospital).

Changes in the transmission coefficient

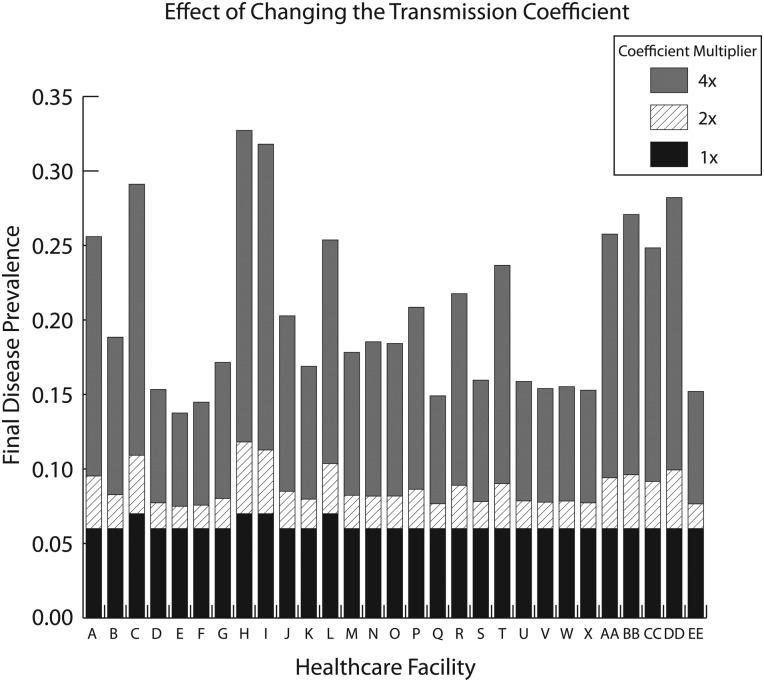
To represent various changes in transmission dynamics (eg, altered pathogen characteristics/behavior, patient mixing, and healthcare worker mixing among patients), a fifth set of experiments explored the effects of doubling and quadrupling the transmission coefficient (table 2) in every hospital. Doubling β increased disease prevalence in OC hospitals by a median of 36.9% (range: 25.4–68.2%), generating a total of 5815 new cases per year countywide (median: 142; range: 13–612 for each hospital). Quadrupling β led to a median 209.9% relative increase in disease prevalence in each hospital (range: 132.4–364.0%), generating a total of 32 272 cases across the county (median: 816 per hospital). Figure 2 shows how the final disease prevalence in each healthcare facility changes with the transmission coefficient.

Figure 2.

Effect of changing the transmission coefficient on final disease prevalence in each healthcare facility.

Discussion

Our study showed how RHEA can generate a virtual laboratory for OC. Different experimental runs demonstrated the impact of various features of the RHEA-generated model and the importance of such explicit representations of healthcare facilities when trying to understand the spread and control of MRSA. Since healthcare facility networks may differ considerably in size, characteristics, and composition, detailed simulations grounded in real-world data may provide different answers compared to much simpler and more theoretical models.^12–18 Previous models have represented infectious disease spread within a single ward or single hospital.^19–26 Some models have looked at a limited number of facilities with gross representations of each facility (ie, not explicitly representing each ward and unit). Many existing studies utilize theoretical or structured population models with limitations such as fixed hospital capacity,^{18 27} limits on patient transfers or clustering,^{12 17 18} limited data sources,^{14 17 18} equal bed sizes,^{17 18} no readmission,¹⁷ random mixing,^{12 17} and homogeneous patient populations.²⁷ While theoretical models are helpful in generating hypotheses, deciding among and implementing policies and interventions may necessitate more detailed simulations grounded in extensive actual data.

One challenge in simulation modeling is to include enough detail to adequately answer relevant questions, but not too much detail to obscure relationships. Indeed, our study identified parameters that could substantially affect the results of simulation experiments (eg, differentiating between the LOS for disease patients versus non-disease patients could alter infectious disease spread, suggesting the importance of further exploring how an infectious disease may affect LOS). We also demonstrated that representing specific facility details matters. In other words, assuming that facilities are the same (eg, same LOS, bed capacity, and patient sharing relationships) can yield different results and conclusions.

RHEA's initial primary target audience is infection control specialists and other stakeholders (eg, public health officials) interested in controlling healthcare-associated infections. RHEA could serve as a virtual laboratory to test new policies, interventions, and technology in specific regions of interest before their implementation. Once the model is built, RHEA could be used by hospital administrators, public health officials, policy makers, third party payers, manufacturers, and other decision makers. This, in turn, could save them the considerable time, effort, and expense that trial and error would bring. Since the impact of a policy or intervention may differ by location or circumstances, RHEA offers the ability to rapidly create a simulation model of a specific healthcare system and region, thereby bypassing the time and effort entailed in building a new simulation model of a region completely from scratch. We have begun to utilize RHEA to test the effects of different infection control interventions.^{28 29} Our ultimate goal is to create a friendly user interface for stakeholders to directly use RHEA.

Limitations

All models by definition are simplifications of real life and cannot represent every possible factor.³⁰ Our model does not include co-morbidities that may affect disease transmission or mortality outcomes, and disease outcomes were not validated. Although patients in real life can re-enter the ICU from the general wards, to prevent multiple movements to and from these wards during a single stay, we set the probability of ICU entry from the general wards to zero. Patients in real life can also transfer directly from the ICU to another facility. We also do not represent healthcare facilities outside of OC that may exchange patients with OC facilities (although 86% of patients stay within OC for care). In addition, our model included only adult patients and not pediatric patients. We also did not consider community transmission.

Conclusions

A decision maker can utilize RHEA to generate a detailed ABM of any healthcare system of interest to serve as a virtual laboratory to test different policies and interventions. As healthcare systems become larger and more complex, there may an increasing need for such a tool. The impact of a policy or intervention may differ by location and circumstance. Our study also demonstrated the importance of including different facility-specific details based on real-world data.