Modeling Multiscale Subbands of Photographic Images with Fields of Gaussian Scale Mixtures

Abstract

The local statistical properties of photographic images, when represented in a multi-scale basis, have been described using Gaussian scale mixtures. Here, we use this local description as a substrate for constructing a global field of Gaussian scale mixtures (FoGSMs). Specifically, we model multi-scale subbands as a product of an exponentiated homogeneous Gaussian Markov random field (hGMRF) and a second independent hGMRF. We show that parameter estimation for this model is feasible, and that samples drawn from a FoGSM model have marginal and joint statistics similar to subband coeffcients of photographic images. We develop an algorithm for removing additive white Gaussian noise based on the FoGSM model, and demonstrate denoising performance comparable with state-of-the-art methods.

I. Introduction

MANY successful methods in image processing and computer vision rely on statistical models for images, and it is of continuing interest to develop improved models, both in terms of their ability to precisely capture image structures, and their practicality for use in applications. A common method of constructing such statistical models is to first identify statistical properties of photographic images, and then develop probabilistic models that capture these properties. The first step in this process is to choose a representation (typically, a linear basis) in which the statistical properties are more simply described. Early research in image statistics was based primarily on pixel and Fourier representations. But over the past two decades, numerous studies have demonstrated that linear image decompositions based on multi-scale multi-orientation localized basis functions (loosely referred to as “wavelets”) are particularly effective in revealing statistical regularities of photographic images. For instance, wavelet coefficients of photographic images generally have highly kurtotic non-Gaussian marginal distributions [1], [2], [3], and the amplitudes of nearby coefficients are strongly correlated [4], [5], [6].

A variety of parametric models have been proposed to capture these regularities, including the generalized Laplacian [7], [8], [9], [10], the Bessel K [11], the multi-variate Student's t-distribution [12], the α-stable family [13] and the Cauchy distribution [14]. All of these non-Gaussian statistical models can be unified under the flexible semi-parametric density family known as Gaussian scale mixtures (GSMs) [15], [16]. By definition, a GSM density is an infinite mixture of zero-mean Gaussian variables with covariances related by multiplicative scaling. GSMs can emulate many of the non-Gaussian statistical behaviors observed in local groups of wavelet coefficients of photographic images. In addition, the underlying Gaussian structure leads to relatively simple parameter learning and inference procedures. For these reasons, local image models based on GSMs have been highly successful when applied to image denoising [17], [18].

Despite this success, it has proven difficult to extend the local GSM description to a consistent global probability model. One can partition the coefficient space into non-overlapping clusters, and describe each of these using an independent GSM. But such a model will ignore important statistical dependencies between coefficients in adjacent blocks. The inhomogeneities that arise from treating coefficients near block boundaries differently from those in the center can, in turn, lead to noticeable artifacts such as blocking or aliasing in applications. This problem may be somewhat ameliorated by using overlapping (e.g., convolutional) blocks [17], [18]. But then treating these blocks as independent samples is not consistent with any global model. Another option is to retain non-overlapping coefficient clusters, but to capture the dependencies between these clusters by linking the hidden scaling variables in a tree-structured Markov model (e.g., [19], [20]). Although these models are able to capture some global statistical dependencies, they still produce artifacts due to the inhomogeneous treatment of spatially proximal coefficients that are assigned to different branches of the tree.

A natural means of extending the local GSM description to a homogeneous global description is through the use of Markov random fields (MRFs). A MRF is a global model uniquely determined by a local statistical description. A number of authors have developed MRF-based image models in the pixel domain (e.g., [21], [22], [23], [24], [25], also see [26] for an overview). In particular, the recently developed field of experts model [27] has been used to achieve impressive performance in denoising. However, these MRF-based models usually involve learning and inference procedures based on statistical sampling, which are generally computationally costly or unstable.

In this paper, we take a different approach to embedding a local GSM description within a global consistent MRF, by modeling multi-scale subbands as fields of Gaussian scale mixtures (FoGSMs). Specifically, a FoGSM is formed by an element-wise product of two mutually independent MRFs: a homogeneous Gaussian MRF (hGMRF), and a positive-valued MRF obtained by exponentiating a second hGMRF. The former captures second-order dependencies, while the latter characterizes the variability and dependencies of local variance. Individual coefficients in the FoGSM model marginally follow a GSM distribution, while the global MRF structure generates dependencies beyond local neighborhoods. We develop a parameter estimation procedure, exploiting the computational advantages of the underlying hGMRFs, and demonstrate that samples from FoGSMs share important statistical properties of photographic images. As an example application, we develop a Bayesian denoising methodology using FoGSM as a prior model for clean images. We show that the resulting denoising method achieves performance comparable to state-of-the-art methods. Preliminary results of this work have been presented in [28].

II. Background

A. Photographic image statistics

Photographic images exhibit distinct statistical regularities that are especially apparent when they are represented using a multi-scale basis (loosely referred to as a “wavelet” decomposition). To be more specific, the wavelet coefficients of photographic images tend to have highly kurtotic non-Gaussian marginal distributions [1], [2], [3]. More importantly, even when they are second-order decorrelated, there are higher-order statical dependencies between coefficients at nearby locations, orientations and scales [5], [6], [16]. Shown in Fig. 1 are empirical joint and conditional histograms for five pairs of subband coefficients of the “boat” image, corresponding to basis functions with spatial separations of Δ = {1, 4, 32} samples, two orthogonal orientations and two adjacent scales. For adjacent coefficients, we observe an approximately elliptical joint distribution. This behavior was originally reported for Hilbert-transform pairs of basis functions [30], and later generalized to pairs at different positions, orientations and scales [5], [6]. The “bow-tie” shaped conditional distribution indicates that the variance of one coefficient depends on the value of the other. This is a highly non-Gaussian behavior, since the conditional variances of a jointly Gaussian density are always constant, independent of the value of the conditioning variable. For coefficients that are distant, the dependency becomes weaker and the corresponding joint and conditional histograms become more separable, as would be expected for two independent random variables. Finally, although the examples shown here were generated using a particular multi-scale oriented image representation, these statistical properties are fairly robust to the specific choice of decomposition as long as the basis functions are localized and band-pass.

Fig. 1.

Histograms of pairs of subband coefficients of four photographic images, decomposed using a Steerable Pyramid decomposition [29]. Top: Contour plots of joint histograms, drawn at equal intervals of log probability. Bottom: Conditional histograms, computed by independently normalizing each column of the joint histogram. Image intensities are proportional to probability, except that each column of pixels is independently rescaled so that the largest probability value is white.

B. Gaussian scale mixtures

A Gaussian scale mixture (GSM) vector is defined as the product of a zero-mean Gaussian vector and an independent positive scalar variable. Specifically, a d-dimensional GSM vector x can be constructed as $\mathbf{x}=\sqrt{z}\cdot \mathbf{u}$, where u is a d-dimensional zero mean Gaussian vector, and $z\in {\mathcal{R}}^{+}$ is independent of x. The density of x is determined by the covariance matrix, Σ, of the Gaussian vector, and the density of z:

$$p\left(\mathbf{x}\right)={\int }_z{\mathcal{N}}_{\mathbf{x}}(0,z\Sigma )p_z\left(z\right)dz={\int }_z\frac{1}{\sqrt{{\left(2\pi z\right)}^d\mid \Sigma \mid }}\text{exp}\left(-\frac{{\mathbf{x}}^T{\Sigma }^{-1}\mathbf{x}}{2z}\right)p_z\left(z\right)dz.$$ (1)

As a family of probability densities, GSM includes many common kurtotic distributions, including all those mentioned in the introduction [15]. For instance, if z follows an inverse gamma distribution, the resulting GSM density reduces to a multivariate Student's t-distribution [15], [31].

C. Homogeneous Gauss-Markov random fields

A Markov random field (MRF) is a global joint distribution on a mesh of nodes that is uniquely determined by the local density of each node conditioned on the nodes in a surrounding neighborhood. In particular, the MRF is the maximal entropy density consistent with the local probabilistic constraints [26]. A Gaussian MRF (GMRF) is one in which all the local conditional (and hence, joint) densities are Gaussian. In this case, the inverse covariance matrix (also known as the precision matrix) of the full set of nodes contains a zero entry for all pairs of nodes that are not within each other's conditioning neighborhoods. The sparse form of the precision matrix means that it usually provides a more convenient parameterization of a GMRF than the full covariance matrix. A homogeneous GMRF (hGMRF) is a GMRF with local density parameters invariant to absolute spatial location. In particular, when the hGMRF is defined over a two-dimensional lattice with circular boundary handling¹, its precision matrix is block circulant (see Appendix A for details), determined by the generating kernel $\mathcal{Q}$ that captures nonzero dependencies within each neighborhood. Given the relatively small set of parameters, the block circulant structure, and the resulting close relationship with the discrete Fourier transform (see Appendix A), hGMRFs are significantly more computationally tractable than general MRFs in terms of parameter estimation, sampling, and inference. Learning and sampling with hGMRFs are described in Appendix B and C, respectively, and a more detailed description of GMRFs and hGMRFs may be found in reference [32].

III. Fields of Gaussian scale mixtures

The GSM model has been used successfully to describe the statistics of local clusters of multiscale image coefficients, which can include spatial neighbors as well as coefficients in adjacent scale and orientation subbands [e.g., 19]. But, as mentioned in the introduction, extending local GSM model to a global model of images without introducing either statistical inconsistencies, or inhomogeneities in the global model structure is difficult. Here, we resolve this dilemma by describing each subband as a homogeneous Field of Gaussian Scale Mixtures (FoGSM).

We define a FoGSM as the element-wise product of two mutually independent MRFs, u and $\sqrt{\mathbf{z}}$:

$$\mathbf{x}\stackrel{d}{=}\mathbf{u}\otimes \sqrt{\mathbf{z}},$$ (2)

where the square root is applied to each component of z. Here, u is a zero-mean Gaussian MRF, and z is a positive-valued MRF of scaling variables. To eliminate the scaling ambiguity between u and z, we assume that each component of u has unit variance. The FoGSM model inherits from the GSM model the construction as a product of an independent Gaussian variable and another positive random variable, and as such, all one-dimensional marginal densities of a FoGSM are GSMs. But unlike the local GSM model, in which a single z variable is multiplied by every component of a multivariate Gaussian variable u, the Gaussian components in FoGSM each have their own z variable. This collection of z variables form a second MRF, which can capture higher-order statistical dependencies.

To further reduce the number of free parameters in the model, we use homogeneous FoGSMs to model each subband in a multiscale decomposition. Specifically, we assume u to be a zero-mean homogeneous Gaussian MRF (hGMRF), with circular boundary handling:

$$p\left(\mathbf{u}\right)\propto \sqrt{\mid \mathcal{C}\left({\mathcal{Q}}_u\right)\mid }\text{exp}\left(\frac{-{\mathbf{u}}^T\mathcal{C}\left({\mathcal{Q}}_u\right)\mathbf{u}}{2}\right),$$ (3)

where ${\mathcal{Q}}_u$ is the generating kernel, and $\mathcal{C}\left({\mathcal{Q}}_u\right)$ is a block circulant precision matrix formed from that kernel. Furthermore, we assume that z is derived by applying a point-wise exponential “link” function to a second hGMRF. Alternatively, we can define log z (where the log operator is applied element-wise) as a zero-mean hGMRF with precision matrix $\mathcal{C}\left({\mathcal{Q}}_z\right)$:

$$p_{\mathbf{z}}\left(\mathbf{z}\right)\propto \frac{\sqrt{\mid \mathcal{C}\left(Q_z\right)\mid }}{\prod _i{z}_i}\text{exp}\left(\frac{-{\left(\log \mathbf{z}\right)}^T\mathcal{C}\left({\mathcal{Q}}_z\right)\left(\log \mathbf{z}\right)}{2}\right).$$ (4)

The inter-dependencies between components of z may be explicitly incorporated through the precision matrix $\mathcal{C}\left({\mathcal{Q}}_z\right)$. This log-normal random field is a natural extension of the univariate log-normal density used previously for the scalar multiplier in a local GSM model [33].

The density of x conditioned on z, may be easily written by substituting the element-wise quotient $\mathbf{x}\oslash \sqrt{\mathbf{z}}$ for the vector u in Eq. (6) and re-normalizing:

$$\begin{array}{cc}\hfill p(\mathbf{x}\mid \mathbf{z})& \propto \sqrt{\frac{\mid \mathcal{C}\left({\mathcal{Q}}_u\right)\mid }{\prod _i{z}_i}}\text{exp}\left(\frac{-{(\mathbf{x}\oslash \sqrt{\mathbf{z}})}^T\mathcal{C}\left({\mathcal{Q}}_u\right)(\mathbf{x}\oslash \sqrt{\mathbf{z}})}{2}\right)\hfill \\ \hfill & =\sqrt{\frac{\mid \mathcal{C}\left({\mathcal{Q}}_u\right)\mid }{\prod _i{z}_i}}\text{exp}\left(\frac{-{\mathbf{x}}^T\mathcal{D}{\left(\sqrt{z}\right)}^{-1}\mathcal{C}\left({\mathcal{Q}}_u\right)\mathcal{D}{\left(\sqrt{\mathbf{z}}\right)}^{-1}\mathbf{x}}{2}\right).\hfill \end{array}$$ (5)

where $\mathcal{D}\left(\sqrt{\mathbf{z}}\right)$ in the second line denotes a square diagonal matrix generated from vector $\sqrt{\mathbf{z}}$. The resulting conditional density on x is a zero-mean inhomogeneous GMRF, as its precision matrix $\left[\mathcal{D}{\left(\sqrt{\mathbf{z}}\right)}^{-1}\mathcal{C}\right({\mathcal{Q}}_u\left)\mathcal{D}{\left(\sqrt{\mathbf{z}}\right)}^{-1}\right]$ no longer has a block circulant structure.

A. Learning and sampling FoGSMs

A FoGSM density on subband coefficients x is determined by the generating kernels of the two constituent hGMRFs, ${\mathcal{Q}}_u$ and ${\mathcal{Q}}_z$. When fitting FoGSM to data, it is also desirable to have an estimate of the field z. Thus, we formulate the learning of FoGSM as simultaneous estimation of parameters ${\mathcal{Q}}_z$ and ${\mathcal{Q}}_u$ and variables ${\left\{{\mathbf{z}}_i\right\}}_{i=1}^N$, from a training set of subbands ${\left\{{\mathbf{x}}_i\right\}}_{i=1}^N$, as

$$\underset{{\left\{{\mathbf{z}}_i\right\}}_{i=1}^N,{\mathcal{Q}}_u,{\mathcal{Q}}_z}{\text{argmax}}\log p({\left\{{\mathbf{x}}_i\right\}}_{i=1}^N,{\left\{{\mathbf{z}}_i\right\}}_{i=1}^N;{\mathcal{Q}}_u,{\mathcal{Q}}_z).$$ (6)

Optimization of this objective function corresponds to a combination of maximum likelihood estimation of the model parameters (${\mathcal{Q}}_z$, ${\mathcal{Q}}_u$) and maximum a posteriori estimation of the hidden variables ${\left\{{\mathbf{z}}_i\right\}}_{i=1}^N$ from training data ${\left\{{\mathbf{x}}_i\right\}}_{i=1}^N$.

We optimize equation (6) using a coordinate ascent scheme, which alternates between maximizing each of ${\left\{{\mathbf{z}}_i\right\}}_{i=1}^N$, ${\mathcal{Q}}_u$ and ${\mathcal{Q}}_z$ while holding the remaining two fixed:

$$\begin{array}{cc}\hfill \left(i\right){\mathbf{z}}_i^{(t+1)}& ={\text{argmax}}_{\mathbf{z}}\log p({\mathbf{x}}_i,{\mathbf{z}}_i;{\mathcal{Q}}_u^{\left(t\right)},{\mathcal{Q}}_z^{\left(t\right)})\text{for}i=1,\cdots ,N\hfill \\ \hfill \left(ii\right){\mathcal{Q}}_u^{(t+1)}& ={\text{argmax}}_{{\mathcal{Q}}_u}\log p({\{{\mathbf{x}}_i,{\mathbf{z}}_i^{(t+1)}\}}_{i=1}^N;{\mathcal{Q}}_u,{\mathcal{Q}}_z^{\left(t\right)})\hfill \\ \hfill \left(iii\right){\mathcal{Q}}_z^{(t+1)}& ={\text{argmax}}_{Q_z}\log p({\{{\mathbf{x}}_i,{\mathbf{z}}_i^{(t+1)}\}}_{i=1}^N;{\mathcal{Q}}_u^{(t+1)},{\mathcal{Q}}_z)\hfill \end{array}$$ (7)

Running the three steps in (7) iteratively guarantees convergence to a local maximum of the objective function in (6). Each step may be further simplified.

The objective function in step (i) of Eq. (7) is more conveniently expressed in terms of the element-wise inverse square root of variable z. We define $\mathbf{s}=1\oslash \sqrt{\mathbf{z}}$, from which z can be recovered using $\mathbf{z}=1\oslash (\mathbf{s}\otimes \mathbf{s})$. The conditional density of x given s may then be written:

$$\begin{array}{cc}\hfill p(\mathbf{x}\mid \mathbf{s})& \propto \prod _i{s}_i\text{exp}\left(\frac{-{(\mathbf{x}\otimes \mathbf{s})}^T\mathcal{C}\left({\mathcal{Q}}_u\right)(\mathbf{x}\otimes \mathbf{s})}{2}\right)\hfill \\ \hfill & =\prod _i{s}_i\text{exp}\left(\frac{-{\mathbf{s}}^T\left[\mathcal{D}\right(\mathbf{x}\left)\mathcal{C}\right({\mathcal{Q}}_u\left)\mathcal{D}\right(\mathbf{x}\left)\right]\mathbf{s}}{2}\right),\hfill \end{array}$$ (8)

and the density of s may be easily obtained by suitable transformation of the density of z:

$$p\left(\mathbf{s}\right)\propto \frac{1}{\prod _i{s}_i}\text{exp}\left(-2{\left(\log \mathbf{s}\right)}^T\mathcal{C}\left({\mathcal{Q}}_z\right)\left(\log \mathbf{s}\right)\right).$$ (9)

Using these new definitions, step (i) in Eq. (7) may be rewritten as

$$\begin{array}{cc}\hfill \widehat{\mathbf{s}}& \triangleq \underset{\mathbf{s}}{\text{argmax}}\log p(\mathbf{x},\mathbf{s};{\mathcal{Q}}_u{\mathcal{Q}}_z)\hfill \\ \hfill & =\underset{\mathbf{s}}{\text{argmax}}\log p(\mathbf{x}\mid \mathbf{s};{\mathcal{Q}}_u)+\log p(\mathbf{s};{\mathcal{Q}}_z)\hfill \\ \hfill & =\underset{\mathbf{s}}{\text{argmin}}\{\begin{array}{c}\frac{1}{2}{\mathbf{s}}^T\left[\mathcal{D}\right(\mathbf{x}\left)\mathcal{C}\right({\mathcal{Q}}_u\left)\mathcal{D}\right(\mathbf{x}\left)\right]\mathbf{s}+2{\left(\log \mathbf{s}\right)}^T\mathcal{C}\left({\mathcal{Q}}_z\right)\left(\log \mathbf{s}\right)\hfill \end{array}\phantom{\}}.\hfill \end{array}$$ (10)

This objective function may be optimized with conjugate gradient descent [34]. Much of the computation involves multiplying vectors by the precision matrix. Because the precision matrix is block-circulant, these operations are convolutions and may be efficiently implemented using the fast Fourier transform. Empirically, we also found that the conjugate gradient iteration converges quickly: After roughly 300 steps of iteration for a 512 × 512 pixel image, the successive relative changes in the objective function are less than 10⁻¹³.

Steps (ii) and (iii) in (7) correspond to estimating model parameters ${\mathcal{Q}}_u$ and ${\mathcal{Q}}_z$ given data ${\{{\mathbf{x}}_i,{\mathbf{z}}_i\}}_{i=1}^N$. Specifically, step (ii) may be simplified to

$$\begin{array}{cc}\hfill {\widehat{\mathcal{Q}}}_u& =\underset{{\mathcal{Q}}_u}{\text{argmax}}\log p(\mathbf{x},\mathbf{z};{\mathcal{Q}}_u,{\mathcal{Q}}_z)\hfill \\ \hfill & =\underset{{\mathcal{Q}}_u}{\text{argmax}}\log p(\mathbf{x}\mid \mathbf{z};{\mathcal{Q}}_u)\hfill \\ \hfill & =\underset{{\mathcal{Q}}_u}{\text{argmax}}\log p(\mathbf{x}\oslash \mathbf{z};{\mathcal{Q}}_u)\hfill \end{array}$$ (11)

where the last line corresponds to a maximum likelihood estimate of the generating kernel ${\mathcal{Q}}_u$ of a zero-mean hGMRF given N independent samples ${\{{\mathbf{x}}_i\oslash \sqrt{{\mathbf{z}}_i}\}}_{i=1}^N$.

Similarly, step (iii) may be simplified as

$$\begin{array}{cc}\hfill {\widehat{\mathcal{Q}}}_z& =\underset{{\mathcal{Q}}_z}{\text{argmax}}\log p(\mathbf{x},\mathbf{z};{\mathcal{Q}}_u{\mathcal{Q}}_z)\hfill \\ \hfill & =\underset{{\mathcal{Q}}_z}{\text{argmax}}\log p(\mathbf{z};{\mathcal{Q}}_z)\hfill \\ \hfill & =\underset{{\mathcal{Q}}_z}{\text{argmax}}\log p(\log \mathbf{z};{\mathcal{Q}}_z)\hfill \end{array}$$ (12)

which is the maximum likelihood estimate of parameter ${\mathcal{Q}}_z$ in a hGMRF on log z given independent samples ${\left\{\log {\mathbf{z}}_i\right\}}_{i=1}^N$. Again, both steps allow efficient computation based on the properties of block circulant matrices. The details of parameter estimation for hGMRFs are provided in Appendix B.

Sampling from FoGSM is simple and efficient. By definition, a sample of FoGSM is formed by element-wise multiplication of two independent samples of u and $\sqrt{\mathbf{z}}$. The former is obtained by sampling from hGMRF u, and the latter is obtained by element-wise exponentiation of the square root of a sample of hGMRF log z. Sampling from each two-dimensional hGMRF is implemented by linearly transform a sample of white Gaussian noise, which is again efficient due to the computational advantages of block circulant matrices. We provide basic descriptions of these operations in Appendix C and more information can be found in [32].

IV. Modeling multi-scale image subbands with FoGSMs

In this section, we investigate empirically how well a FoGSM is able to account for the statistical properties of subband coefficients of photographic images. We fit an independent FoGSM model to each subband of a photographic image, and examine the properties of the u and log z fields, as well as samples from the learned FoGSM model.

A. Experimental setup

Our data sets are multi-scale subbands of a given orientation and scale from five standard test images of size 512 × 512 pixels (“Lena”, “Barbara”, “boats”, “hill”, and “baboon”). For image representation, we employed an over-complete tight frame representation known as the steerable pyramid [29] as the front-end linear decomposition. The basis functions of this linear decomposition are spatially localized, oriented and span roughly one octave in bandwidth. They are polar separable in the Fourier domain and are related by translation, dilation and rotation. We fit the FoGSM model to subbands corresponding to the first scale and third orientation in an 8-orientation decomposition (the peak orientation angle of this band is at π/4 radians, relative to the horizontal axis).

The neighborhood size of the two component hGMRFs of the FoGSM model (corresponding to variables u and log z) were chosen by maximizing the cross-validated likelihood. We cut each subband into equal-sized rectangular halves, fitted the FoGSM model of a given neighborhood size to one half of the subband, and then computed the likelihood on the data from the other half of the subband using Eq. (6). The best performance was observed for 5 × 5 neighborhoods, for both hGMRFs. Once the neighborhood size was determined, the generating kernels were optimized using the algorithm described in the previous section. The vector z, which represents the local signal variance, was initialized by computing the local variances estimated within each overlapping 5 × 5 spatial window.

B. Decomposition and parameters

Shown in the top row of Fig. 2 are the results of decomposing a subband from the “boats” image according to the fitted FoGSM model. Specifically, the subband (left panel) is decomposed into the product of the u field (middle panel) and the $\sqrt{\mathbf{z}}$ field (right panel, in logarithm) using the training algorithm described in Section III-A. Visually, we can see that the changing spatial variances are captured by the estimated log z, and residual homogeneous structures are captured by the estimated u. The second row in Fig. 2 are the marginal histograms of each field in the log domain, plotted against a Gaussian density of the same variance. Note that the marginal distribution of u is well approximated by a Gaussian, as assumed in the FoGSM model. The marginal distribution of log z, while unimodal, exhibits noticeable deviations from Gaussianity. In particular, it is clearly asymmetric, and this property seems to be consistent across a variety of di erent subbands and images.

Fig. 2.

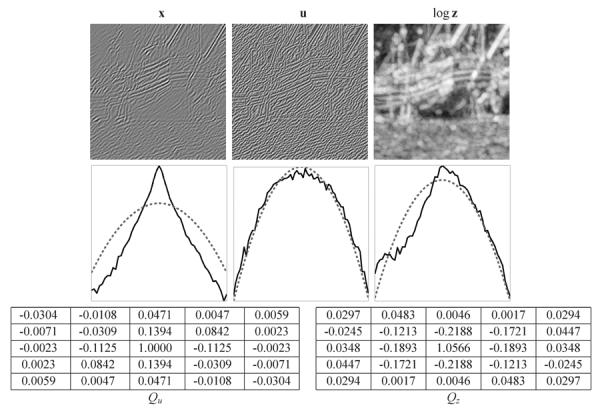
Top: Decomposition of a subband from image “boat” (left) into a hGMRF u (middle) and the corresponding multiplier field log z (right). Each image is rescaled individually to fill the full range of grayscale intensities. Middle: log marginal histograms of x, the estimated u and the estimated log z. Dotted lines correspond to Gaussian density of the same mean and variance. Bottom: 5 × 5 central non-zero regions for the hGMRF generating kernels of the estimated u and log z fields.

Shown in the bottom row of Fig. 2 are the estimated 5 × 5 generating kernels ${\mathcal{Q}}_u$ and ${\mathcal{Q}}_z$. The former reflects the orientation anisotropy of hGMRF u, which is matched to the orientation tuning of the subband. On the other hand, ${\mathcal{Q}}_z$ shows only weak orientation preference. We could interpret this to indicate that the MRF for log z is close to isotropic. However, visual inspection of the log z field suggests that the MRF frequently exhibits strongly oriented content, but that this content is inhomogeneous (i.e., the orientation is di erent in different image regions) and thus cannot be captured by a homogeneous GMRF. Furthermore, one can see that the estimated u and log z are not independent, as assumed by the FoGSM model, but have aligned structures (typically arising from image contours).

C. Statistics of FoGSM samples

The statistical dependencies captured by the FoGSM model can be further illustrated by examining marginal and joint statistics of samples from the fitted model. Note that this is achieved by fitting the global FoGSM statistical model to a subband, and then drawing samples from this model, not by explicitly adjusting parameters to fit the marginal or joint histograms (as was done in [16]).

We begin by comparing the marginal distributions of the samples and the original subband. Figure 3 shows empirical histograms in the log domain of a particular subband from four different photographic images (dashed line), and those of the synthesized samples of FoGSM models learned from each corresponding subband (solid line). For comparison, a Gaussian with matching standard deviation is also displayed (thin dashed line). Note that the synthesized samples have conspicuous non-Gaussian marginal characteristics, exemplified by the high peak and heavy tails, similar to the image subbands. On the other hand, the synthesized coefficients are typically less kurtotic than the real subbands. The shape of these marginal densities is dictated by the z field, which is a hGMRF transformed with a point-wise exponential link function. An alternative choice of link function could be used to create distributions closer to the observed wavelet subbands.

Fig. 3.

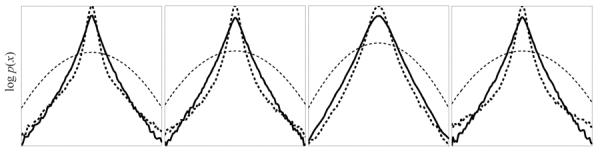
Marginal log distributions of coefficients from a multi-scale decomposition of four photographic images (dashed line), synthesized FoGSM samples from the same subband (solid line), and a Gaussian with the same standard deviation (thin dashed line).

In addition to the marginal statistics, the FoGSM model also has joint behaviors that are similar to those observed in multi-scale coefficients of photographic images. Shown in Fig. 4 are the joint and conditional histograms of synthesized samples from the FoGSM model estimated from the same subband used to generate the histograms in Fig. 1. Note that histograms of the synthesized samples have a dependence on spatial proximity similar to those of the image data shown in Fig. 1. This behavior arises directly from the structure of the FoGSM model. The random field z is smooth, and thus nearby components have nearly identical marginal variance, resulting in an elliptically contoured joint density, and strong dependency between coefficients. This dependency is propagated from neighborhood to neighborhood in the FoGSM model, but weakens with distance. On the other hand, note that the dependencies between coefficients representing different orientations or scales are not properly modeled, because we have used an independent FoGSM to model each subband. This is evident when comparing the fourth and the fifth columns of Figs. 4 and 1.

Fig. 4.

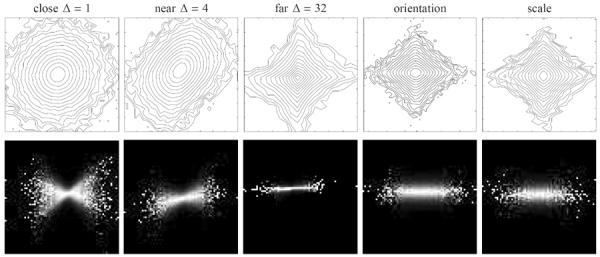
Joint distribution of pairs of subband coefficients obtained from samples drawn from the best-fitting FoGSM model. See the caption of Fig. 1 for explanation.

Finally, Fig. 5 shows samples of u, log z, and x drawn according to a FoGSM model whose parameters were fit to the subband shown in Fig. 2. The u field resembles that of the subband, but the z field is seen to lack the extended structures seen in the data. Thus, the FoGSM model fails to fully capture the inhomogeneous long-range interactions that arise in images around contours or extended features.

Fig. 5.

A sample from the hGMRFs with parameters shown in Fig. 2.

V. Application to image denoising

As a probability model for photographic images, FoGSM may be used as a prior for Bayesian estimation of an image given an observation corrupted by additive white Gaussian noise of known variance. In addition to its practical relevance, image denoising is a simple yet powerful test for the effectiveness of an image model, providing a clear quantitative test of how well the model can differentiate photographic image content from noise.

A. Algorithm

We follow a conventional methodology, decomposing the noise-corrupted image into wavelet subbands, computing an estimate of the coefficients of each subband using the FoGSM model as a prior, and then generating the denoised image by applying the inverse wavelet transform to the denoised subbands. Since the wavelet transform is linear, we may write y = x+w for a wavelet subband of the noisy image, where x is the clean wavelet subband and w is the noise that is added to the subband. Note that in an over-complete representation such as steerable pyramid, white Gaussian noise in the image domain is transformed into correlated Gaussian noise, whose covariance can be computed from the basis functions of the transform.

A standard approach to denoising is to formulate it as a Bayesian inference problem, selecting an estimate based on the posterior density p(x|y), which is proportional to the product of the likelihood function p(y|x) and the image prior p(x). Two solutions are common. The maximum a posterior (MAP) estimate is the mode of the posterior density, ${\widehat{\mathbf{x}}}_{\mathit{MAP}}={\text{argmax}}_{\mathrm{x}}\log p(\mathbf{x}\mid \mathbf{y})$, whereas the Bayesian least square (BLS) estimate, which minimizes the expected square error between the restored image and the original image, is the mean of the posterior density ${\widehat{\mathbf{x}}}_{\mathit{BLS}}=E(\mathbf{x}\mid \mathbf{y})$. Both of these solutions involve computationally expensive (high-dimensional) integration when used with FoGSM model. Specifically, MAP requires a high-dimensional integral over z, while BLS requires high-dimensional integrals over both x and z.

Although it is possible to obtain approximations to these solutions using Markov chain Monte-Carlo sampling [26] or variational approximations [35], we instead develop a deterministic algorithm that takes advantage of the hGMRF structure of the FoGSM model. Specifically, we compute

$$(\widehat{\mathbf{x}},\widehat{\mathbf{z}})=\underset{\mathbf{x},\mathbf{z}}{\text{argmax}}\log p(\mathbf{x},\mathbf{z}\mid \mathbf{y})$$ (13)

and then take $\widehat{\mathbf{x}}$ as the denoised subband. This strategy, known as a “partial optimal solution” [36], greatly reduces the computational complexity of the problem. The solution to the optimization problem in Eq. (13) is found by coordinate ascent. Starting with initial values for x and z, the algorithm proceeds by alternating between the following steps:

• 1)
  Optimization of x: Given the current estimate of z, the optimization of x in (13) can be expanded using Bayes' rule:

  $$\begin{array}{cc}\hfill \underset{\mathbf{x}}{\text{argmax}}\log p(\mathbf{x},\mathbf{z}\mid \mathbf{y})& =\underset{\mathbf{x}}{\text{argmax}}\left\{\log p\right(\mathbf{y}\mid \mathbf{x},\mathbf{z})+\log p(\mathbf{x}\mid \mathbf{z})+\log p(\mathbf{z})-\log p(\mathbf{y}\left)\right\}\hfill \\ \hfill & =\underset{\mathbf{x}}{\text{argmax}}\left\{\log p\right(\mathbf{y}\mid \mathbf{x})+\log p(\mathbf{x}\mid \mathbf{z}\left)\right\},\hfill \end{array}$$

  where the first term is simplified because y and z are independent when conditioned on x, and the last two terms are dropped because they do not depend on x. Given the Gaussian structure of the first two terms, the maximum is linear in y (equivalent to a Wiener filter). Specifically, we must minimize a quadratic expression:

  $$\underset{\mathbf{x}}{\text{argmin}}\{\begin{array}{c}{(\mathbf{y}-\mathbf{x})}^T\mathcal{C}{\left(C_w\right)}^{-1}(\mathbf{y}-\mathbf{x})+{\mathbf{x}}^T\mathcal{D}{\left(\sqrt{\mathbf{z}}\right)}^{-1}\mathcal{C}\left({\mathcal{Q}}_u\right)\mathcal{D}{\left(\sqrt{\mathbf{z}}\right)}^{-1}\mathbf{x}\hfill \end{array}\phantom{\}}$$

  where the noise covariance $\mathcal{C}\left(C_w\right)$ is a block-circulant matrix determined by a generating kernel C_w that represents the convolution by which the subband is obtained from the image pixels. Note that although $\mathcal{C}\left(C_w\right)$ may be sparse (zero beyond the support of the filters), the inverse of $\mathcal{C}\left(C_w\right)$ can still be dense. It is therefore computationally advantageous to work with $\mathcal{C}\left(C_w\right)$ rather than its inverse. For this reason, we introduce $\mathbf{t}=\mathcal{C}{\left(C_w\right)}^{-1}\mathbf{x}$, and find the optimal t by solving

  $$\underset{\mathbf{t}}{\text{argmin}}\{\begin{array}{c}{(\mathbf{y}-\mathcal{C}(C_w\left)\mathbf{t}\right)}^T\mathcal{C}{\left(C_w\right)}^{-1}(\mathbf{y}-\mathcal{C}(C_w\left)\mathbf{t}\right)+{\mathbf{t}}^T\mathcal{C}{\left(C_w\right)}^T\mathcal{D}{\left(\sqrt{\mathbf{z}}\right)}^{-1}\mathcal{C}\left({\mathcal{Q}}_u\right)\mathcal{D}{\left(\sqrt{\mathbf{z}}\right)}^{-1}\mathcal{C}\left(C_w\right)\mathbf{t}\hfill \end{array}\phantom{\}}$$

  or, expanding the first line, and dropping the term independent of t:

  $$\underset{\mathbf{t}}{\text{argmin}}\{\begin{array}{c}{\mathbf{t}}^T\mathcal{C}\left(C_w\right)\mathbf{t}-2{\mathbf{y}}^T\mathbf{t}+{\mathbf{t}}^T\mathcal{C}{\left(C_w\right)}^T\mathcal{D}{\left(\sqrt{\mathbf{z}}\right)}^{-1}\mathcal{C}\left({\mathcal{Q}}_u\right)\mathcal{D}{\left(\sqrt{\mathbf{z}}\right)}^{-1}\mathcal{C}\left(C_w\right)\mathbf{t}\hfill \end{array}\phantom{\}}$$

  Note that this the objective function is quadratic in t, guaranteeing a global optimal solution. We compute the optimum using conjugate gradient descent, and then recover the optimal x through the relationship $\widehat{\mathbf{x}}=\mathcal{C}\left(C_w\right)\widehat{\mathbf{t}}$.
• 2)
  Optimization of z: Given the current estimate of x, the optimization of z in (13) can be written as

  $$\underset{\mathbf{z}}{\text{argmax}}\log p(\mathbf{x},\mathbf{z}\mid \mathbf{y})=\underset{\mathbf{z}}{\text{argmax}}\left\{\log p\right(\mathbf{y}\mid \mathbf{x},\mathbf{z})+\log p(\mathbf{x},\mathbf{z})-\log p(\mathbf{y}\left)\right\}.$$

  The last term may be dropped because it is independent of z, and the first term is dropped since y is independent of z when conditioned on x. Thus, the problem is reduced to argmax_z log p(x, z), which may be computed as in step (i) of the learning procedure of Sec. III-A.
• 3)
  Acceleration: The alternating optimization of x and z is guaranteed to converge to a local optimum of the objective function in Eq. (13), but the convergence speed can be very slow. To accelerate convergence, we include a heuristic “inertial” step after every two steps of the optimization loop. Specifically, the algorithm takes a step in the direction established by the optimal values of the previous two iterations, with the step size optimized according to:

  $$\{{\widehat{\mathbf{x}}}^{(k+1)},{\widehat{\mathbf{z}}}^{(k+1)}\}=\underset{\alpha \in (0,{\alpha }_{max})}{\text{argmax}}\log p\left({\widehat{\mathbf{x}}}^{\left(k\right)}+\alpha ({\widehat{\mathbf{x}}}^{\left(k\right)}-{\widehat{\mathbf{x}}}^{(k-1)}),{\widehat{\mathbf{z}}}^{\left(k\right)}+\alpha ({\widehat{\mathbf{z}}}^{\left(k\right)}-{\widehat{\mathbf{z}}}^{(k-1)})\mid \mathbf{y}\right)$$

  Intuitively, such a jump ensures that the optimization does not oscillate back and forth within a narrow valley of the objective function. In practice, as shown in the following experiments, it achieves a substantial reduction in the overall running time of the algorithm.
• 4)
  Parameter estimation (optional): The denoising algorithm described thus far assumes the model parameters ${\mathcal{Q}}_u$ and ${\mathcal{Q}}_z$ are known. These model parameters can be learned as a generic statistical model for wavelet coefficients from a large set of noise-free photographic images using the algorithm provided in Section III-A. The advantage of a generic image model approach is that the training can be performed offline, which may greatly reduce the overall running time. Alternatively, these parameters can be adaptively learned by including a parameter estimation step in the loop of the denoising algorithm

  $$({\widehat{\mathbf{Q}}}_{\mathbf{u}}^{\left(k\right)},{\widehat{\mathbf{Q}}}_{\mathbf{z}}^{\left(k\right)}=\underset{{\mathbf{Q}}_{\mathbf{u}},{\mathbf{Q}}_{\mathbf{z}}}{\text{argmax}}\log p({\widehat{\mathbf{x}}}^{\left(k\right)},{\widehat{\mathbf{z}}}^{\left(k\right)}\mid \mathbf{y};{\mathbf{Q}}_{\mathbf{u}},{\mathbf{Q}}_{\mathbf{z}})$$ (14)

  as in Section III-A. The FoGSM model parameters (${\mathcal{Q}}_u$, ${\mathcal{Q}}_z$) are estimated from hGMRFs $[\mathbf{x}\oslash \sqrt{{\widehat{\mathbf{z}}}^{\left(k\right)}}]$ and $\left[\log {\mathbf{z}}^{\left(k\right)}\right]$, as in steps (ii) and (iii) of Eq. (7). Adaptively learning the parameters allows the model to better account for the local structure of the image in question, thus potentially leading to better performance. We compare the relative performance of these two training schemes in the following experiments.

B. Experimental setup

We evaluated the FoGSM denoising method on a set of standard grayscale test images [17]. All images are of size 256 × 256 or 512 × 512 pixels and in 8-bit TIFF format. Noisy images were generated by adding simulated white Gaussian noise. We evaluate the denoising performance by visual inspection, as well as the conventional objective performance known as peak-signal-to-noise-ratio (PSNR), defined as 20 log₁₀(255/σ_e), with σ_e the standard deviation (computed by averaging over spatial position) of the difference between the restored image and the original image.

Each noise-corrupted image was first decomposed into a steerable pyramid with multiple scales (5 levels for a 512×512 image and 4 levels for a 256 × 256 image) and 8 orientations. These values were chosen empirically as a trade-off between denoising performance and computational load. The resulting representation is approximately 11 times over-complete, relative to the original image size. The Markov neighborhoods for hGMRFs u and log z were both chosen to cover 5 × 5 blocks of coefficients, since this was found to be optimal for representation of clean images. We verified that this specific choice was also roughly optimal for the best denoising performances across different images and noise levels. The model parameters were obtained by training the FoGSM model adaptively for each subband as described in Section V-A, with initial parameter values chosen to represent a smooth and isotropic GMRF. The initial values of x and z are computed from subband denoised with the local GSM model [17].

C. Results

Denoising results for six test images, at seven different noise levels, are reported in Table I. The standard deviations of PSNR values for each image and noise level, computed by repeating the each denoising experiment 10 times with different samples of noise, are consistently lower than 0.1dB. In addition to the results for our FoGSM algorithm, we also provide denoising results of the BLS-GSM method [17]. This algorithm computes the Bayes least squares estimate (i.e., conditional mean) of individual coefficients based on a local GSM model. The comparison with FoGSM allows us to assess the gain in performance that is obtained by building a global model. We employed the implementation described in [17], which assumes a neighborhood consisting of 3 × 3 spatial neighbors plus a “parent” coefficient in the next coarsest scale². Finally, we provide results of the current state-of-the-art denoising method, BM3D [37]. The PSNR values for these methods were directly taken from corresponding publications. Note that the FoGSM algorithm achieves consistent improvements in PSNR over the local GSM based algorithm (average improvement is 0.52dB), clearly demonstrating the advantage of a globally consistent statistical model. On the other hand, the performance of the FoGSM method is comparable (sometimes better, sometimes worse) to that of BM3D, which is not based on any explicit statistical model. In general, BM3D relies on the image containing repeating patterns (specifically, many blocks of pixels that are similar). Thus it performs best on images with large regions of the same texture (e.g., “Barbara”), or long contours of similar orientation (e.g., “House”), and performs less well on images with diverse content (e.g., “boats”, or “Lena”).

TABLE I.

Comparison of FoGSM denoising results with those of the local BLS-GSM method [17], and the recently published BM3D method [37], which represents the current state-of-the-art.

σ/PSNR	Barbara 512 × 512			boats 512 × 512			hill 512 × 512
	FoGSM	GSM	BM3D	FoGSM	GSM	BM3D	FoGSM	GSM	BM3D
5/34.15	38.65	37.79	38.31	37.39	36.97	37.28	37.16	36.91	37.14
10/28.13	35.01	34.03	34.98	34.12	33.58	33.92	33.78	33.38	33.62
15/24.61	32.85	31.86	33.11	32.31	31.70	32.14	31.99	31.51	31.86
25/20.17	30.10	29.13	30.72	30.03	29.37	29.91	29.91	29.37	29.85
50/14.15	26.40	25.48	27.17	27.01	26.38	26.64	27.38	26.82	27.08
75/10.63	24.29	23.65	25.10	25.33	24.79	24.96	25.93	25.46	25.58
100/8.13	23.01	22.61	23.49	24.20	23.75	23.74	24.88	24.53	24.45

σ/PSNR	house 256 × 256			Lena 512 × 512			peppers 256 × 256
	FoGSM	GSM	BM3D	FoGSM	GSM	BM3D	FoGSM	GSM	BM3D
5/34.15	38.98	38.65	39.83	38.66	38.49	38.72	37.91	37.30	38.12
10/28.13	35.63	35.35	36.71	35.94	35.61	35.93	34.38	33.73	34.68
15/24.61	33.89	33.64	34.94	34.28	33.90	34.27	32.34	31.70	32.70
25/20.17	31.64	31.40	32.86	32.11	31.69	32.08	29.78	29.18	30.06
50/14.15	28.51	28.26	29.37	29.12	28.61	28.86	26.43	25.93	26.41
75/10.63	26.69	26.41	27.20	27.37	26.84	27.02	24.53	24.11	24.48
100/8.13	25.33	25.11	25.50	26.12	25.64	25.57	23.17	22.80	22.91

Performance values are expressed as PSNR, 20 log₁₀(255/σ_e), where σ_e is the standard deviation of the difference between the denoised image and the original image. Numbers in boldface indicate the best performance among the three methods for each image and noise level. Cases in which the two best methods differ by less than 0.1dB (the averaged standard deviation of the PSNR values) are considered a tie.

In Fig. 6 we plot the PSNR performance of four recent denoising methods relative to that of FoGSM. The performance of FoGSM is consistently better than those of the kSVD method [39], the BLS-GSM method [17], and the fields of experts (FoE) [27], and (on average) comparable to those of BM3D [37], which currently represents the state-of-the-art.

Fig. 6.

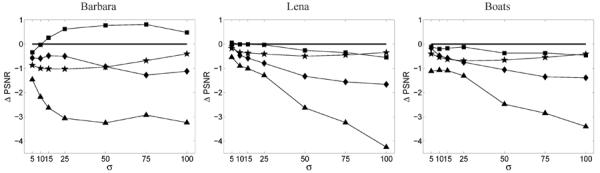
Performance comparison of denoising methods for three different images. Plotted are differences in PSNR for different input noise levels (σ) between FoGSM and four other methods (■ BM3D [37], ★ BLS-GSM [17], ◆ kSVD [39] and ▴ FoE [27]). The PSNR values for these methods were taken from corresponding publications.

Next, we examine and compare the denoising results visually. Shown in Fig. 7 and Fig. 9 are the results of denoising the “Barbara” image and the “boats” image with noise level σ = 50, corresponding to a peak-signal-to-noise-ratio (PSNR) of 14.15 dB. We have chosen a relatively high level of noise, in order to provide a clear visualization of the capabilities and limitations of the model. To better examine the details of the denoising results, we show in Fig. 8 and 10 cropped regions of each of the corresponding images in Fig. 7 and 9, respectively. For these examples, the FoGSM denoising achieves substantial improvements (+0.95 and +0.68 dB) and is seen to exhibit higher contrast and continuation of oriented features. However, FoGSM also introduces some noticeable artifacts in low contrast regions, which are likely due to failures of the FoGSM model to capture all statistical properties of photographic image wavelet coefficients. For example, coefficient amplitudes are known to be correlated across scale (see Fig. 4, right panel). If represented properly, this correlation should allow the denoising algorithm to recognize isolated large coefficients as noise, since (unlike photographic images) they will not have corresponding large-amplitude coefficients in adjacent bands. But the current model treats each subband independently, thus allowing these isolated coefficients to remain as unsuppressed artifacts. In addition, these artifacts may also be aggravated by the use of a MAP-like estimator. A local MAP-GSM estimator produces similar unsuppressed coefficients, when compared to the smoother behavior of the local BLS-GSM estimates.

Fig. 7.

Denoising results using local GSM [17] and FoGSM.

Fig. 9.

Denoising results using local GSM [17] and FoGSM. Performances are evaluated in peak-signal-to-noise-ratio (PSNR), 20 log₁₀(255/σ_e), where σ_e is the standard deviation of the error between the restored image and the original image.

Fig. 8.

Zoom-up regions of the images in Fig. 7.

Fig. 10.

Zoom-up regions of the images in Fig. 9.

The denoising performance obtained with FoGSM is attained with a substantial computational cost. As a rough indication, our unoptimized Matlab code, running on an Intel workstation with 2.6 Ghz dual Opteron 64-bit processor and 16 Gb RAM memory, takes on average of 97.3 mins (results averaging over 9 trials, with a range of [71.8,124.4] mins) to denoise a 512 × 512 image at noise level σ = 50, and takes on average of 35.3 mins (result averaging over 4 images, with a range of [28.4, 47.9] mins), to denoise a 256×256 image at the same noise level. It is likely these values could be improved by incorporating additional acceleration heuristics.

D. Algorithm variations

In order to understand the contribution of various aspects of the FoGSM-based denoising method, we examined their relative effect on the denoising performance. Shown in Table II are the changes in PSNR and running time when various features of the method are modified. All results are for noise level σ = 50 and averaged over three 512 × 512 images (“boats”, “Lena”, “Barbara”). The first two columns correspond to modifications of the front-end representation. The first (ortho wvlt) corresponds to using an approximately orthogonal wavelet decomposition based on quadrature mirror filters [40]. The separable QMF pyramid splits the image frequency domain into horizontal, vertical and mixed diagonal subbands. Using this representation results in a substantial reduction in performance, which we believe is partly due to the mixed orientations in the diagonal band, and partly due to the lack of over-completeness which generally improves denoising [41], [42].

TABLE II.

Effects of different algorithm variations.

	ortho wvlt	4 orns	3 × 3 nb	7 × 7 nb	gen param	no accl
ΔPSNR (dB)	−0.47	−0.32	−0.07	−0.17	−0.39	0.01
Δt/t (%)	−62.8	−52.6	−1.2	2.5	−41.7	163.8

ΔPSNR specifies the changes in PSNR resulting from a change in the corresponding attribute. Δt/t specifies the percentage of change in running time relative to the running time of the standard algorithm described in Section V-C. All values are averages over three 512 × 512 images (“boats”, “Lena”, “Barbara”) for the noise level σ = 50.

The second column (4 orns) shows the result of using steerable pyramid decomposition with only four orientations (instead of eight). Decreasing the number of orientations leads to a significant drop in performance, accompanied by a substantial reduction in running time. On the other hand, increasing the number of orientations (not shown) leads to small improvements in PSNR, at the expense of considerable computation cost.

In the next three columns, we examine the effects in the FoGSM model structure. We first compared the effect of different choices of MRF neighborhood size (3 × 3 and 7 × 7). As shown, changing neighborhood size has relatively little effect on the overall running time, but the PSNR values were lower for both neighborhood sizes, justifying our choice of the 5 × 5 neighborhood (at least for this image and noise level). In the fifth column (gen param), we compared the result of off-line training of the (${\mathcal{Q}}_u$, ${\mathcal{Q}}_z$) parameters of the FoGSM model on a set of noise-free images (not including the three test images). This leads to a significant reduction in the computational cost of denoising an image, since the parameter learning step no longer needs to be included in the denoising process. However, this is accompanied by a significant loss in denoising performance (an average PSNR reduction of approximately 0.4dB), since the generically learned model parameters are less adapted to the idiosyncrasies of the specific image/subband being denoised. The last column (no accel) shows that the accelerating heuristics introduced in previous section significantly improve the running time of the denoising procedure, while having a negligible effect on PSNR.

VI. Related Models

The local GSM model that underlies the FoGSM is closely related to other local hidden variable models for images [5], [16], [8], [31], [44], [43]. However, the use of MRFs in the FoGSM allow it to extend to images of arbitrary size in a statistically consistent way, while the local scale mixture models are essentially confined to describing small image patches. The underlying MRF structure of the hidden variables in the FoGSM model also differentiates it from mixture models with tree-structured hidden variables [19], [20]. These models have the advantage of explicitly capturing cross-band dependencies, but they suffer from spatial inhomogeneities introduced by the tree partitioning.

As a global MRF-based image model, the basic architecture of FoGSM differs from existing non-Gaussian MRF image models [21], [23], [24], [27] in that it is not defined by specification of clique potentials, but through non-linear composition of two hGMRFs. On the other hand, FoGSM has some resemblance to the compound Gauss-Markov random fields model for images [22], which is formed by modulating a homogeneous GMRF with a binary line process that indicates the existence of an edge between two spatial locations [21]. A modified version, proposed in [36], treats the hidden variables as independent. This simplifies computation, but may lead to a loss in performance in applications.

VII. Discussion

We have introduced fields of Gaussian scale mixtures as a flexible and efficient tool for modeling the statistics of wavelet coefficients of photographic images. We developed a feasible parameter estimation method, and showed that samples synthesized from the fitted FoGSM model are able to capture structures in the marginal and joint wavelet statistics of photographic images. And we have applied the FoGSM to image denoising, and demonstrated performance comparable to current state-of-the-art denoising methods.

We envision, and are currently working on, a number of improvements. First, the model should benefit from the introduction of more general Markov neighborhoods, including wavelet coefficients from subbands at other scales and orientations [6], [17], since the current model is clearly not capturing these dependencies. A natural means of achieving this is to allow different subbands to share the same hidden scaling field, although this may substantially complicate the learning and inference algorithms. A possible remedy is to capture these cross-scale dependencies with a coarse-to-fine conditional model. Second, the logarithmic link function used to derive the multiplier field from a hGMRF was chosen somewhat arbitrarily, and we believe that substitution of another non-linear transformation (e.g., a power law, as in [19]) could lead to a more accurate description of marginal and joint image statistics. Finally, there exist residual inhomogeneous structures in both the u and log z fields (see Fig. 2) that can likely be captured by explicitly incorporating local orientation [45] or phase [46] into the model. Finding tractable models and algorithms for handling such angular variables is challenging, but we believe their inclusion will result in substantial improvements in modeling and in denoising performance.

Biographies

Siwei Lyu is an assistant professor in Computer Science at University at Albany, State University of New York. He obtained his B.S. degree in Information Science and M.S. degree in Computer Science, both from Peking University, China, in 1997 and 2000, respectively. From 2000 to 2001, he was an assistant researcher at Microsoft Research Asia. He obtained Ph.D. degree in computer science from Dartmouth College. From 2005 to 2008 he was a post-doctoral research associate at New York University. His research interests include image processing and forensics, machine learning and computer vision.

Eero P. Simoncelli received the B.S. degree, summa cum laude, in Physics in 1984 from Harvard University. He studied applied mathematics at Cambridge University for a year and a half, and then received the M.S. degree in 1988 and the Ph.D. degree in 1993, both in Electrical Engineering from the Massachusetts Institute of Technology. He was an Assistant Professor in the Computer and Information Science department at the University of Pennsylvania from 1993 until 1996. He moved to New York University in September of 1996, where he is currently an Associate Professor in Neural Science and Mathematics. In August 2000, he became an Associate Investigator of the Howard Hughes Medical Institute, under their new program in Computational Biology. His research interests span a wide range of topics in the representation and analysis of visual images, in both machine and biological systems.

Appendix A: Circulant And Block Circulant Matrix

Given a d-dimensional vector (known as a generating kernel)

$$\mathbf{q}={(q{-}_{\lfloor d∕2\rfloor },\cdots ,q_{-1},q_0,q_1,\cdots ,q_{\lfloor d∕2\rfloor -1})}^T,$$

a d × d circulant matrix is constructed as

$$\mathcal{C}\left(\mathbf{q}\right)=\left(\begin{array}{ccccc}\hfill q_0\hfill & \hfill q_1\hfill & \hfill q_2\hfill & \hfill \cdots \hfill & \hfill q_{-1}\hfill \\ \hfill q_{-1}\hfill & \hfill q_0\hfill & \hfill q_1\hfill & \hfill \cdots \hfill & \hfill q_{-2}\hfill \\ \hfill q_{-2}\hfill & \hfill q_{-1}\hfill & \hfill q_0\hfill & \hfill \cdots \hfill & \hfill q_{-3}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill q_1\hfill & \hfill q_2\hfill & \hfill q_3\hfill & \hfill \cdots \hfill & \hfill q_0\hfill \end{array}\right).$$

The rows of $\mathcal{C}\left(\mathbf{q}\right)$ are circularly shifted copies of q^T, and multiplication of $\mathcal{C}\left(\mathbf{q}\right)$ with a d-dimensional vector u is equivalent to convolving vectors q and u, with circular (Dirichlet) boundary handling. The basis functions of the d-sample discrete Fourier transform (DFT) form a complete set of eigenvectors for any circulant matrix, regardless of the choice of generating kernel q. Thus, an alternative means of multiplying by the matrix (q) (generally known as the convolution theorem) is

$$\mathcal{C}\left(\mathbf{q}\right)=F\mathcal{D}\left(\tilde{\mathbf{q}}\right)F^{†}$$

where F is a matrix containing the DFT basis, F^† is the complex-conjugated transpose (used to compute the forward DFT), and $\mathcal{D}\left(\tilde{\mathbf{q}}\right)$ is a diagonal matrix containing the d-point DFT of q. Since the DFT may be implemented with O(d log d) operations, this expression often provides an e cient implementation of convolution with q.

Representation of two-dimensional convolutions (e.g., for images) requires a second-order circulant (also called block circulant) matrix, which can be constructed by recursively applying the circulant structure. Analogous to the circulant matrix, the two-dimensional DFT of the shifted symmetric reflection of $\mathcal{Q}$ are the eigenvalues of $\mathcal{C}\left(\mathcal{Q}\right)$, and the corresponding two-dimensional DFT basis vectors are the eigenvectors. And again, the convolution theorem provides an efficient means of implementing matrix multiplication by the circulant matrix. For a full account of the properties and computations of circulant and block circulant matrices, readers are referred to [47].

Appendix B: Parameter Learning for 2D hGMRF

A zero-mean 2D hGMRF u of dimension N × M is completely determined by the generating kernel $\mathcal{Q}$ of its block circulant precision matrix. The density of u can be expressed as:

$$p\left(\mathbf{u}\right)=\sqrt{\frac{\mid \mathcal{C}\left(\mathcal{Q}\right)\mid }{{\left(2\pi \right)}^{MN}}}\text{exp}\left(-\frac{1}{2}{\mathbf{u}}^T\mathcal{C}\left(\mathcal{Q}\right)\mathbf{u}\right)$$

where we have abused notation a bit by using u to represent the vectorized MRF. Assuming a rectangular Markov neighborhood of size N′ × M′, where M′ ⪡ M and N′ ⪡ N, estimation of $\mathcal{Q}$ corresponds to the determination of the central N′ × M′ entries (all others must be zero).

Given a set of independent samples of u, ${\left\{{\mathbf{u}}_k\right\}}_{k=1}^K$, the generating kernel $\mathcal{Q}$ can be estimated by maximizing the log likelihood:

$$\begin{array}{cc}\hfill L\left(\mathcal{Q}\right)& =\sum _{k=1}^K\log p\left({\mathbf{u}}_k\right)\hfill \\ \hfill & =\frac{K}{2}\log \mid \mathcal{C}\left(\mathcal{Q}\right)\mid -\frac{KMN}{2}\log 2\pi -\frac{1}{2}\sum _{k=1}^K{\mathbf{u}}_k^T\mathcal{C}\left(\mathcal{Q}\right){\mathbf{u}}_k.\hfill \end{array}$$

Using the eigen-decomposition property of block-circulant matrix, and neglecting the constant term, we can write a modified likelihood function as:

$$\begin{array}{cc}\hfill \tilde{L}\left(\mathcal{Q}\right)& =\frac{K}{2}\log \mid F\mathcal{D}\left(\tilde{Q}\right)F^{†}\mid -\frac{1}{2}\sum _{k=1}^K{\mathbf{u}}_k^{T}F\mathcal{D}\left(\tilde{\mathcal{Q}}\right)F^{†}{\mathbf{u}}_k\hfill \\ \hfill & =\frac{K}{2}\log \mid \mathcal{D}\left(\tilde{\mathcal{Q}}\right)\mid -\frac{1}{2}\sum _{k=1}^K{\tilde{\mathbf{u}}}_k^T\mathcal{D}\left(\tilde{\mathcal{Q}}\right){\tilde{\mathbf{u}}}_k,\hfill \\ \hfill & =\frac{K}{2}\sum _{i=1}^{MN}\log {\tilde{\mathcal{Q}}}_i-\frac{1}{2}\sum _{i=1}^{MN}{\tilde{\mathcal{Q}}}_i\sum _{k=1}^K{\left({\tilde{\mathbf{u}}}_k\right)}_i^2.\hfill \end{array}$$

where $\tilde{\mathbf{u}}=F^{†}\mathbf{u}$, the DFT of u. The optimal $\mathcal{Q}$ is then obtained by maximizing $\tilde{L}\left(\mathcal{Q}\right)$ subject to the constraint that the solution must be a symmetric and positive definite matrix. It can be shown that $\tilde{L}\left(\mathcal{Q}\right)$ is a convex function, and the constraints form a convex set in the feasible space of $\mathcal{Q}$. Thus, solving for the optimal $\mathcal{Q}$ is a convex optimization problem and there are a variety of iterative solutions that are guaranteed to converge to the global optimum [48].

Appendix C: Sampling 2D hGMRF

A sample of a zero-mean 2D hGMRF u of dimension N × M with precision $\mathcal{C}\left(\mathcal{Q}\right)$ can be obtained from a sample of white Gaussian noise w of the same dimension, by computing

$$\mathbf{u}=F\mathcal{D}{\left(\sqrt{\tilde{\mathcal{Q}}}\right)}^{-1}{F}^{†}\mathbf{w},$$ (15)

That is, compute the DFT of the noise, divide (element-wise) by the square root of the DFT of the desired generating kernel, $\tilde{\mathcal{Q}}$, and then invert the DFT. A similar algorithm has been used for texture synthesis [49] as well as for Monte Carlo sampling for image restoration [50].

It is easy to verify that the resulting MRF has the desired covariance structure:

$$\begin{array}{cc}\hfill E\left({\mathbf{uu}}^T\right)& =E\left[F\mathcal{D}{\left(\sqrt{\tilde{\mathcal{Q}}}\right)}^{-1}{F}^{†}{\mathbf{ww}}^T{F}^{†}\mathcal{D}{\left(\sqrt{\tilde{\mathcal{Q}}}\right)}^{-1}F\right]\hfill \\ \hfill & =F\mathcal{D}{\left(\sqrt{\tilde{\mathcal{Q}}}\right)}^{-1}{F}^{†}E\left({\mathbf{ww}}^T\right)F^{†}\mathcal{D}{\left(\sqrt{\tilde{\mathcal{Q}}}\right)}^{-1}F\hfill \\ \hfill & =F\mathcal{D}{\left(\tilde{\mathcal{Q}}\right)}^{-1}{F}^{†}=\mathcal{C}{\left(\mathcal{Q}\right)}^{-1},\hfill \end{array}$$

where we have used the Hermitian property of matrix F and the fact that E(ww^T) = I.