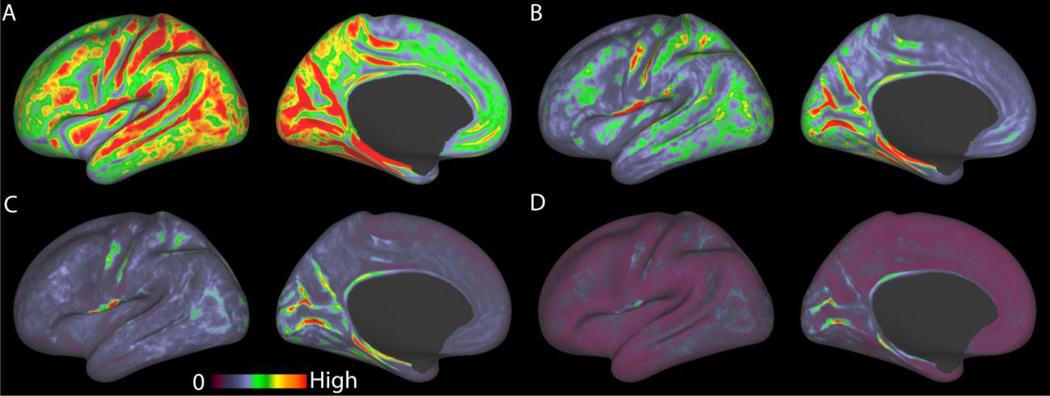
Figure 5.

A comparison of the geometrical effects of various fMRI acquisition resolutions on folded cortex averaged across the Q1 20 unrelated HCP subjects all on the same color scale. A, 4mm isotropic, B, 3mm isotropic, C, 2.5mm isotropic, D, 2mm isotropic. When mapping fMRI data of a given resolution to the midthickness surface, larger voxels can artificially increase the correlation between geodesically distant surface vertices, as larger voxels can span both sides of a sulcus or a thin gyral blade of white matter. The measure being displayed is calculated for each vertex by finding the set of vertices that could potentially share a voxel's data with the selected vertex during volume to surface mapping with trilinear interpolation. For each of the vertices in this set, we compute the expected correlation to the selected vertex that would result from mapping a white noise timeseries by trilinear interpolation, aligned such that a voxel center is located midway between the two vertices. We then multiply by the geodesic distance between the vertices in order to upweight the measure for the vertices that are far apart across the surface. Finally the maximum of the measure is taken over the set of vertices found to be in range. This model is a significant simplification of the problem, however, as it does not account for the variable pointspread function of BOLD at 3T or the effects of larger draining veins. The model also uses a simple trilinear interpolation volume to surface mapping method instead of the more complicated ribbon-based method used in the pipelines below. This model does, however, point to the potential benefits of higher acquisition resolution in reducing the induced cross-sulcal and cross gyral correlations between vertices that are far apart along the surface (and thus potentially lying in different cortical areas), but close together in the volume.