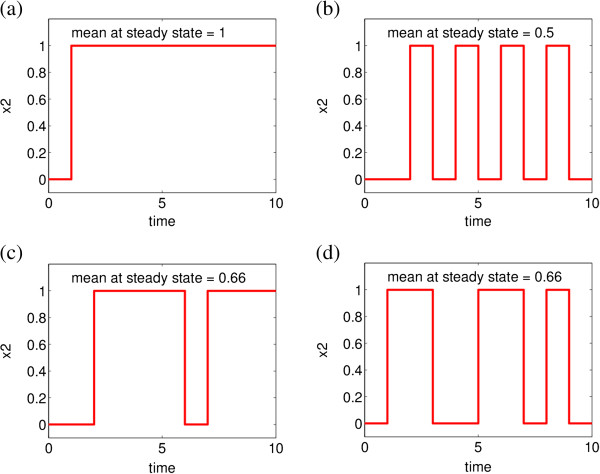
Figure 4.

Dynamical simulations of node x₂ of the example network in Figure2, with initial state k = 000. (a) Dynamics of x₂ governed by the constituent BN corresponding to the transition function f₁, where c₁ = 1, c₂ = c₃ = c₄ = 0. Starting from 000 the periodic attractor {011,111} is reached. The probability of {x₂ = 1} given by the stationary distribution is 1. (b) Dynamics of x₂ governed by the constituent BN corresponding to the transition function f₄, where c₄ = 1, c₁ = c₂ = c₃ = 0. Starting from 000 the periodic attractor {001,111} is reached. The probability of {x₂ = 1} given by the stationary distribution related to the reached attractor, i.e., $[0,\frac{1}{2},0,0,0,0,0,\frac{1}{2}]$ (the states are considered in the lexicographical order), is 0.5. (c,d) Examples of x₂ dynamics in the full PBN as given in Figure 2. Starting from 000 different trajectories are obtained for different simulation runs. The underlying Markov chain is ergodic and a unique stationary distribution, being the steady state (limiting) distribution, exists therefore. The steady state probability of {x₂ = 1} is 0.66.