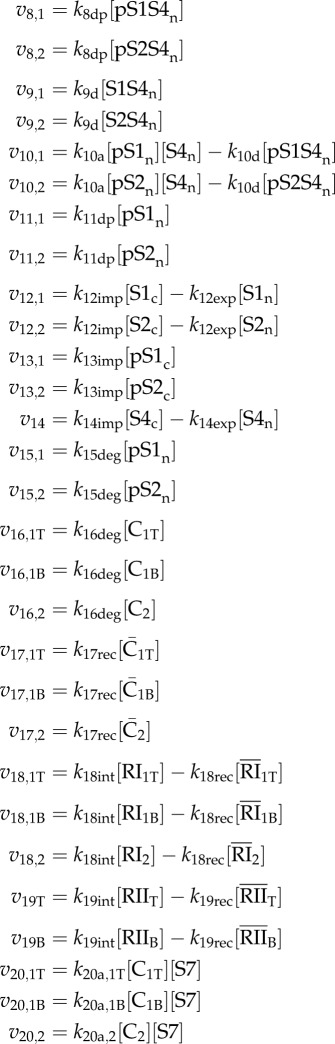Abstract
The transforming growth factor-β (TGF-β) signal transduction pathway controls many cellular processes, including differentiation, proliferation and apoptosis. It plays a fundamental role during development and it is dysregulated in many diseases. The factors that control the dynamics of the pathway, however, are not fully elucidated yet and so far computational approaches have been very limited in capturing the distinct types of behaviour observed under different cellular backgrounds and conditions into a single-model description. Here, we develop a detailed computational model for TGF-β signalling that incorporates elements of previous models together with crosstalking between Smad1/5/8 and Smad2/3 channels through a negative feedback loop dependent on Smad7. The resulting model accurately reproduces the diverse behaviour of experimental datasets for human keratinocytes, bovine aortic endothelial cells and mouse mesenchymal cells, capturing the dynamics of activation and nucleocytoplasmic shuttling of both R-Smad channels. The analysis of the model dynamics and its system properties revealed Smad7-mediated crosstalking between Smad1/5/8 and Smad2/3 channels as a major determinant in shaping the distinct responses to single and multiple ligand stimulation for different cell types.
Keywords: transforming growth factor-β signal transduction pathway, coupled signalling and crosstalk, negative feedback loop, signal transduction, transforming growth factor-β superfamily network, computational modelling of signalling pathways
1. Introduction
The transforming growth factor-β (TGF-β) superfamily of cytokines controls a diverse range of cellular responses, including proliferation, differentiation and apoptosis [1]. It plays a fundamental role during development and in maintenance of tissue homeostasis [2]. Defective TGF-β signalling and alterations of the main pathway components have been identified in a number of human diseases, including autoimmune and cardiovascular diseases, developmental disorders and cancer [3–5].
The TGF-β superfamily of ligands initiates signalling by binding to two types of transmembrane serine-threonine kinase receptors, namely type I and type II receptors, at the cell surface (plasma membrane) and activating the downstream signalling cascade. Typically, the ligand binds to the constitutively active type II receptors on the cell surface, and subsequently the resulting ligand–receptor complex recruits the type I receptor, which is phosphorylated by the type II receptor [6]. In turn, this active heteromeric signalling receptor complex is internalized, which allows it to recruit and phosphorylate cytosolic receptor-regulated Smad (R-Smad) proteins. Further downstream, the phosphorylated R-Smads are released from the active ligand–receptor complex, bind to Smad4, the common mediator Smad (Co-Smad), and translocate across the nuclear membrane, accumulating in the nucleus. The nuclear phosphorylated R-Smad–Co-Smad complexes act as transcription factors, binding to DNA and regulating the expression of hundreds of genes in a cell-type-specific and context-dependent fashion [7].
This superfamily of ligands stimulates downstream signalling through the activation of two R-Smad channels, centralized about Smad1/5/8 and Smad2/3 phosphorylation. Among the type I receptors, ALK4/5/7 specifically phosphorylate Smad2 and Smad3, while ALK1/2/3/6 phosphorylate Smad1, Smad5 and Smad8 [7]. The latter group is often associated with bone morphogenetic protein (BMP) induction, while the former are activated in response to TGF-β, Nodal or Activin. However, the potential combinatorial interactions in the macromolecular assembly of the active ligand–receptor complexes among the 33 known members of the TGF-β superfamily of ligands with five type II and seven type I receptors in mammalian cells, for instance, could lead to potential crosstalk between channels [8] and to the activation of both channels by a single ligand [9]. In particular, the TGF-β ligand induces phosphorylation of Smad2 and Smad3 through the recruitment of ALK5 to the ligand–receptor complex, but it has also been shown to activate the Smad1/5/8 channel in a number of cell lines. In these cases, while still binding to the same type II receptor (TGF-β type II receptor, denoted here by RIIT), the ligand–receptor complex recruits ALK1 in endothelial cells [10] and ALK5 alone or in conjunction with another type I receptor from the ALK1/2/3/6 group in several other cell types [11–14] leading to Smad1 phosphorylation.
Several mechanisms exist at each step of the signal transduction pathway that contribute to the regulation of the signal [15]. Particularly important for the TGF-β pathway are receptor trafficking [16] and Smad nucleocytoplasmic shuttling [17]. At the plasma membrane, receptors are constitutively internalized and recycled, tightly regulating the number of active receptors at the cell surface [16,18]. Similarly, Smad proteins and R-Smad complexes are constitutively shuttled across the nuclear membrane, providing an avenue for sensing receptor activity and reflecting changes into the nucleus [17]. In addition, Smad proteins undergo proteasomal degradation, dephosphorylation, sequestration and direct inhibition of their transcriptional activity [2].
An additional layer of signalling regulation occurs through negative feedback control mediated by the inhibitory Smads (I-Smads), namely Smad6 and Smad7 [15]. Indeed, members of the TGF-β superfamily induce transcription of the Smad6 and Smad7 genes [19,20] through binding of nuclear R-Smad complexes to Smad6 and Smad7 promoters [2]. I-Smads inhibit TGF-β superfamily signalling through several mechanisms, with Smad6 preferentially blocking BMP signalling and Smad7 blocking both TGF-β and BMP signalling. Smad6 has been reported to bind to phosphorylated Smad1 thus preventing the formation of the active pSmad1–Smad4 species [21], but typically competes with the R-Smads for receptor binding [22]. Smad7 similarly blocks R-Smad recruitment to the receptors [23], and induces receptor degradation through Smurf-dependent ubiquitination [24,25]. I-Smads can also inhibit responses at the transcriptional level, for instance by recruiting Smad co-repressors to DNA [15].
Quantitative approaches and predictive models have been successfully applied to the TGF-β signal transduction pathway, providing a means to functionally understand the key mechanisms and processes underpinning experimental results [8,26–37]. Specifically, receptor trafficking and the dynamics of ligand–receptor complexes have been shown to be a crucial signal-processing component [8,34]. Additionally, Smad activation and nucleocytoplasmic shuttling have been shown to provide a mechanism for faithfully transmitting cytosolic signals into the nucleus, which adds an additional layer of signal control [29,33]. Melke et al. [31] developed an endothelial-cell-based model, incorporating dynamics of two R-Smad channels with an I-Smad negative feedback mechanism, but with simplified receptor mechanics. Paulsen et al. [32] have also explored negative feedback control in this system with respect to BMP-derived developmental patterns in vertebrate embryos. Zi & Klipp [35] and Chung et al. [28] combined aspects of the previously developed models into detailed receptor/Smad models without dynamic I-Smad negative feedback. Recently, these models have been extended to investigate the unique signalling responses of the system under a variety of experimental and theoretical conditions [27,36,37].
Here, we develop a novel detailed computational model for TGF-β signalling that incorporates elements of previous models together with crosstalking between Smad1/5/8 and Smad2/3 channels. Crosstalking is mediated by a negative feedback loop dependent on Smad7 that impacts receptor degradation and its ability to transmit the signal through the R-Smad phosphorylation. We incorporate detailed receptor trafficking and Smad nucleocytoplasmic shuttling through both R-Smad channels together with the addition of the ligand-induced negative feedback loop. We apply this model to three distinct cell lines—human keratinocytes (HaCaT), bovine aortic endothelial cells (BAEC) and mouse mesenchymal cells (C2C12)—in order to investigate the underlying mechanisms that define their varying response to ligand stimulation. The resulting mathematical description provides further insight into the control mechanisms of this signal transduction pathway, which are key to its dynamics and broad range of functions. Our results indicate that this negative feedback mechanism is sufficient to characterize the differing signal duration and dynamics between the two R-Smad channels in the three cell types, while the effects of coupled signalling among TGF-β family members further differentiate their signalling patterns.
2. Model development and methods
2.1. Model formulation
Our computational model for Smad-dependent signalling considers the main elements of the model developed in the study of Chung et al. [28], which takes into account detailed receptor trafficking, activation of Smad2 upon TGF-β stimulation and Smad nucleocytoplasmic shuttling, and implements both a Smad1-based signalling channel, which can be activated by TGF-β and/or BMP ligands, and a dynamic negative feedback loop through Smad7.
We have characterized the behaviour of the negative feedback loop in HaCaT, BAEC and C2C12 cells. We have chosen these cell types based on the available experimental data on the temporal signalling dynamics of both Smad1 and Smad2 channels upon TGF-β and BMP stimulation and because these three cell lines provide three examples with different properties of the feedback loop.
The full pathway considered in our model, including signalling through TGF-β and BMP (BMP2/BMP6), is illustrated in figure 1 and the different molecular species and their corresponding cellular location are shown in table 1. The arrows in figure 1 indicate reaction steps along the pathway corresponding to the expressions in table 2. The key modules of the model are described in the following subsections, including the details for the three different cell lines.
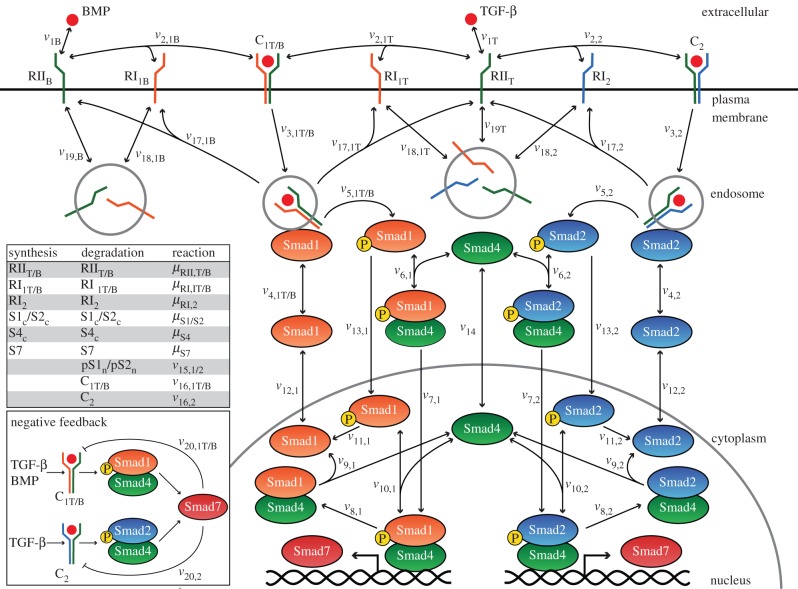
Figure 1.
Schematic of the Smad-dependent TGF-β signalling pathway upon stimulation with TGF-β and BMP. Arrows denote reaction steps, corresponding to the equations in table 2. Synthesis and degradation reactions are provided in the table (inset) with the notation for the different molecular species of table 1. Expression of Smad7 is under the control of a single gene, activated by pSmad1–Smad4 and/or pSmad2–Smad4 nuclear complexes. Smad7 ligand–receptor complex targeting and expression patterns are cell-dependent with all potential combinations illustrated in the inset. Mixed R-Smad complex formation in the HaCaT and C2C12 cases are not explicitly shown here; see text and the caption of table 2 for details of its implementation. (Online version in colour.)
Table 1.
Initial estimates and initial conditions for each molecular species of the model. We used for the molecular species and its descriptions the symbol ‘/’ to indicate ‘or’. For the initial estimate of Smad7, H, B and C denote the values for the HaCaT, BAEC and C2C12 cases, respectively.
| species | description | initial estimate (molecules) | HaCaT initial value (molecules) | BAEC initial value (molecules) | C2C12 initial value (molecules) | compartment |
|---|---|---|---|---|---|---|
| TGF-β | TGF-β in the extracellular medium | 0 | 0 | 0 | 0 | extracellular |
| BMP | BMP2 or BMP6 in the extracellular medium | 0 | 0 | 0 | 0 | extracellular |
| RIIT | TGF-β type II receptor | 5.00 × 102 | 2.88 × 102 | 2.88 × 102 | 2.88 × 102 | plasma membrane |
| RIIB | BMP type II receptor | 5.00 × 102 | 2.88 × 102 | 2.88 × 102 | 2.88 × 102 | plasma membrane |
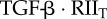 |
complex of TGF-β and type II receptor | 0 | 0 | 0 | 0 | plasma membrane |
 |
complex of BMP2 and type II receptor | 0 | 0 | 0 | 0 | plasma membrane |
| RI1T | TGF-β type I receptor activating the Smad1 channel | 5.00 × 102 | 2.88 × 102 | 2.88 × 102 | 2.88 × 102 | plasma membrane |
| RI1B | BMP type I receptor | 5.00 × 102 | 2.88 × 102 | 2.88 × 102 | 2.88 × 102 | plasma membrane |
| RI2 | TGF-β type I receptor activating the Smad2 channel | 5.00 × 102 | 2.88 × 102 | 2.88 × 102 | 2.88 × 102 | plasma membrane |
| C1T | complex of 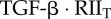 and RI1T and RI1T
|
0 | 0 | 0 | 0 | plasma membrane |
| C1B | complex of 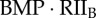 and RI1B and RI1B
|
0 | 0 | 0 | 0 | plasma membrane |
| C2 | complex of 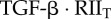 and RI2 and RI2
|
0 | 0 | 0 | 0 | plasma membrane |
 |
internalized 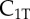
|
0 | 0 | 0 | 0 | endosome |
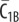 |
internalized C1B | 0 | 0 | 0 | 0 | endosome |
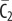 |
internalized C2 | 0 | 0 | 0 | 0 | endosome |
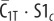 |
complex of 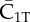 and Smad1 and Smad1 |
0 | 0 | 0 | 0 | endosome |
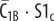 |
complex of 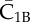 and Smad1 and Smad1 |
0 | 0 | 0 | 0 | endosome |
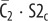 |
complex of 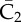 and Smad2 and Smad2 |
0 | 0 | 0 | 0 | endosome |
| S1c/S2c | Smad1/Smad2 | 8.50 × 104 | 4.24 × 104 | 4.24 × 104 | 4.24 × 104 | cytoplasm |
| pS1c/pS2c | phosphorylated Smad1/Smad2 | 0 | 0 | 0 | 0 | cytoplasm |
| S4c | Smad4 | 8.70 × 104 | 4.17 × 104 | 4.17 × 104 | 4.17 × 104 | cytoplasm |
| pS1S4c/pS2S4c | complex of phosphorylated Smad1/Smad2 and Smad4 | 0 | 0 | 0 | 0 | cytoplasm |
| pS1S4n/pS2S4n | complex of phosphorylated Smad1/Smad2 and Smad4 | 0 | 0 | 0 | 0 | nucleus |
| S1S4n/S2S4n | complex of Smad1/Smad2 and Smad4 | 0 | 0 | 0 | 0 | nucleus |
| S1n/S2n | Smad1/Smad2 | 1.50 × 104 | 1.97 × 104 | 1.97 × 104 | 1.97 × 104 | nucleus |
| S4n | Smad4 | 1.30 × 104 | 4.81 × 103 | 5.53 × 103 | 3.47 × 104 | nucleus |
| pS1n/pS2n | phosphorylated Smad1/Smad2 | 0 | 0 | 0 | 0 | nucleus |
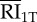 |
internalized RI1T | 4.50 × 103 | 2.88 × 103 | 2.27 × 103 | 2.20 × 104 | endosome |
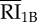 |
internalized RI1B | 4.50 × 103 | 2.88 × 103 | 2.27 × 103 | 2.20 × 104 | endosome |
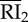 |
internalized RI2 | 4.50 × 103 | 2.88 × 103 | 2.27 × 103 | 2.20 × 104 | endosome |
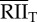 |
internalized RIIT | 4.50 × 103 | 2.88 × 103 | 2.27 × 103 | 2.20 × 104 | endosome |
 |
internalized RIIB | 4.50 × 103 | 2.88 × 103 | 2.27 × 103 | 2.20 × 104 | endosome |
| S7 | Smad7 | H: 3.90 × 104; B/C: 0 | 3.90 × 104 | 0 | 0 | cytoplasm |
Table 2.
Rate equations for each step of the modelled pathway. Equations assigned to μ are production/degradation reactions, while those assigned to v are mass-action kinetic expressions. The former are associated with a particular species, while the latter are numerically ordered to correspond with figure 1. Additionally, the kinetic reactions are specified by the R-Smad channel (1 or 2) and ligand initiating the reaction (T or B for TGF-β or BMP, respectively). Overbars indicate internalized receptor species and c or n represent cytoplasmic or nuclear compounds, respectively. In the HaCaT and C2C12 cases, we account for mixed complex formation by tagging TGF-β-induced pSmad1 spies and preventing the tagged pS1S4n complexes from initiating Smad7 expression (see the electronic supplementary material, table S1).
|
|
2.1.1. Ligand–receptor complex formation
We consider TGF-β, BMP2 and BMP6 ligands freely available and well mixed in the extracellular matrix and at a constant concentration.
The ligand TGF-β first binds to a type II receptor (RIIT), forming the TGF-β · RIIT species, which then recruits a type I receptor, one of the activin receptor-like kinase (ALK) proteins. ALK5 triggers phosphorylation of Smad2/3, stimulating signalling through that branch of the pathway [1]. Smad1/5/8 activation depends on additional type I receptors that can be expressed on the specific cell type. In endothelial cells, it is probably ALK1 [10], while the leading candidate in HaCaT cells is ALK2 [11]. We use RI1T and RI2 to denote the TGF-β-associated type I receptor activating the Smad1 and Smad2 channel, respectively.
An ALK5-dependence for Smad1/5/8 channel activation by TGF-β has been implicated in several cell types, including HaCaT [11], BAEC [38] and C2C12 [14] cell lines. As the mechanism for this process is not fully elucidated, we model Smad1 channel activation through the formation of a TGF-β · RIIT–RI1T complex (denoted here by C1T). The fact that ALK5 receptors are also present in the model and that typically the activity of Smad2 controlled by ALK5 decays more slowly than that of Smad1 [11,14,38] ensures that the model captures the experimental evidence requiring ALK5 receptor for Smad1 phosphorylation.
In a similar fashion, we also include the mechanism for stimulation by BMP2 and BMP6. Through any of the BMP-associated type II receptors (BMPR2, ACVR2A or ACVR2B) and either ALK3 or ALK6, the BMP2 ligand stimulates Smad1/5/8 phosphorylation and the associated downstream signalling processes. The BMP6 ligand signals in a similar manner with the addition of ALK2 as a potential type I receptor partner [39]. It is worth noting that BMP2 provides an entirely separate route from TGF-β for Smad1 channel activation, whereas BMP6 can potentially introduce competition for ALK2 with TGF-β if cells are costimulated with both ligands. Here, we only consider single-ligand treatment for BMP6 in the model, allowing its signalling mechanism to mirror that of BMP2. In both cases, the active ligand–receptor complexes are denoted by C1B.
It is important to emphasize that BMP, in contrast to TGF-β, binds type I and type II receptors in a cooperative manner, which means that BMP is capable of binding to either type of receptor independently but with low affinity unless both types of receptors are present [1]. In all of the experiments that we have analysed, the conditions included saturating concentrations of ligands, which imply that the ligand–receptor complexes are formed very fast independently of the details of the association mechanism between the receptors and ligands. Furthermore, as we maintain a high BMP concentration in all simulations, there is no need to take into account explicitly the cooperative interactions between BMP and their cognate receptors. The differences in ligand–receptor interaction dynamics, in conjunction with receptor trafficking, can lead to distinct BMP signalling dynamics for low ligand concentrations, a situation not considered here. It should be noted that, as a consequence of the different mechanisms for ligand–receptor complex formation, BMP concentrations required for activating Smad1 signalling are higher than those used for TGF-β activation.
2.1.2. Receptor trafficking
TGF-β receptors are constitutively internalized and recycled whether bound to a ligand or free [16,18]. We adopt the methodology developed by Vilar et al. [8] to describe this phenomenon, which has been shown to be a key component in controlling the signal response.
2.1.3. R-Smad activation and oligomerization
Once internalized into the endosomes, active ligand–receptor complexes are able to recruit and phosphorylate cytosolic R-Smad proteins. Upon phosphorylation, the activated R-Smad is released from the active ligand–receptor complex to carry the signal downstream. Both sets of activated R-Smads bind to the Co-Smad in the cytoplasm, forming phosphorylated Smad1–Smad4 (pSmad1–Smad4) or Smad2–Smad4 (pSmad2–Smad4) complexes [7]. We adopt the simplified stoichiometry used by Chung et al. [28] in which the R-Smads only heterodimerize with Smad4.
2.1.4. Smad nucleocytoplasmic shuttling
Smad proteins are constitutively shuttled between nucleus and cytoplasm in the absence of ligand stimulation [40]. While the majority of Smad species are found in the cytosol prior to stimulation, they accumulate in the nucleus upon TGF-β treatment [41]. We use first-order kinetics to model the shuttling processes, along the lines of those developed in the study of Schmierer et al. [33]. The full nucleocytoplasmic shuttling of Smad molecular species is modelled as in the study of Chung et al. [28]. We consider identical shuttling dynamics for both R-Smad channels.
2.1.5. I-Smad-mediated negative feedback loop
Ligands of the TGF-β superfamily can strongly induce transcription of both I-Smad genes [19,20]. In these situations, I-Smad gene expression is controlled by the binding of nuclear active R-Smad complexes, mainly pSmad1–Smad4 and pSmad2–Smad4, to the Smad6 and Smad7 promoter region [2]. We simplify the process of gene transcription and protein production by modelling it as a one-step process relative to the concentration of nuclear pSmad1–Smad4 and pSmad2–Smad4 complexes. This is mathematically characterized by modulating a maximal rate of production by the probability of one of the phospho-R-Smad–Smad4 complexes binding its promoter. Once produced, we consider that the I-Smad is uniformly distributed throughout the cytoplasm. In addition, we consider a single I-Smad species, namely Smad7.
Upon binding to a receptor complex, Smad7 not only inhibits R-Smad activation by competing for receptor binding [23], but also promotes ubiquitin-mediated degradation through recruitment of Smurf1 [25] or Smurf2 [24]. This results in a complex series of steps, which we model as an effective irreversible association reaction between Smad7 and the active ligand–receptor complex. In agreement with the model generated by Paulsen et al. [32], we only consider this receptor interference/degradation mechanism and similarly group Smad6 effects with those of Smad7.
Each of the three cell lines considered here possesses differences in the negative feedback loop—in terms of initial Smad7 concentration, ligand-induced production of Smad7, and Smad7-induced targeting of receptors for degradation—and response to TGF-β stimulation. We have characterized the negative feedback loop for the HaCaT, BAEC and C2C12 cell lines and the key differences are summarized below.
2.1.5.1. HaCaT case
In HaCaT cells, Smad7 protein is present prior to ligand stimulation [42]. Upon treatment with TGF-β, Smad7 protein levels increase slightly before returning to steady-state levels [43]. Through this mechanism, Smad7 provides a relatively static level of inhibition.
In epithelial cells, TGF-β-induced phosphorylated Smad1 can associate with Smad2 rather than with Smad4, forming a mixed R-Smad complex unable to activate transcription of BMP-responsive reporter genes containing BMP-responsive elements (BREs), which bind BMP-induced pSmad1–Smad4 complexes [12]. Experimental evidence suggests that this transcriptionally inactive mixed R-Smad complex is not formed because of a higher affinity for mixed complex formation, but rather the simultaneous presence of both R-Smads at the active ligand–receptor complex [12]. Since the mechanism of this process is not fully elucidated, we incorporate this into the model for HaCaT cell lines by preventing TGF-β-induced nuclear pSmad1–Smad4 complexes from inducing Smad7 expression. In the model, this is accomplished by tagging the pSmad1 species phosphorylated as a result of TGF-β stimulation. These tagged proteins behave identically to their normal counterparts, except that they do not control Smad7 production.
2.1.5.2. BAEC case
In contrast to the behaviour observed in HaCaT cells, a highly dynamic negative feedback mechanism appears to exist in endothelial cells, in which the initial Smad7 concentration is zero or far lower than that of other species [31]. In cells treated with cycloheximide (CHX), an inhibitor of protein biosynthesis in eukaryotic cells, the negative feedback loop is abolished upon TGF-β stimulation, indicating that Smad7 presence requires protein production [44]. In addition, experimental results identify ALK1 as the primary contributor to Smad7 induction. Subsequently, the I-Smad targets the Smad1 channel with higher affinity than that for the Smad2 channel [44]. This establishes a well-defined, auto-regulatory negative feedback loop in endothelial cells.
2.1.5.3. C2C12 case
Similar to the behaviour observed in BAEC cells, C2C12 cells have little Smad7 present prior to ligand stimulation [45]. In this cell line, TGF-β treatment does not lead to transcriptional activation of BMP-responsive reporter genes, suggesting mixed R-Smad complex formation as described in the HaCaT case, whereas the BMP2 ligand is able to strongly induce transcription of these reporter genes controlled by BREs [12]. To incorporate these observations into our model, we allow the Smad2 channel to induce Smad7 production (at the transcriptional level) upon TGF-β stimulation and the Smad1 channel to induce Smad7 production upon BMP (BMP2) stimulation.
Wrighton et al. [14] reported that C2C12 cells are able to activate the Smad1 channel upon TGF-β stimulation independently of ALK1/2/3/6 receptors, relying exclusively on ALK4/5/7. As with the mixed R-Smad complex phenomenon, there is not sufficient mechanistic detail of this signal transduction step. Therefore, in this case, we maintain two separate TGF-β-induced active ligand–receptor complexes (C1T and C2) in the model, one for activation of each R-Smad channel. It has been suggested that ALK5-mediated phosphorylation of Smad1 may involve additional accessory proteins within the active ligand–receptor complex [14]. In our model, this effect is mathematically equivalent to altering the R-Smad affinity for the active ligand–receptor complex or the rate of phosphorylation between channels, which emulates the effect of potential intermediate-protein dependence.
2.1.6. Mathematical model and implementation
The full model, as schematically represented in figure 1, is built upon a system of ordinary differential equations (ODEs) shown in table 3, which are formulated from combinations of the reaction rates of table 2. As done in the study of Chung et al. [28], we compartmentalize the pathway in a single cell with cytosolic and nuclear volumes of 1.13 × 10−12 l and 3.75 × 10−13 l, respectively. This cell is then modelled within 1 ml of extracellular media per million cells [28]. The system for each of the three different cell types and experimental conditions is numerically integrated with the ‘ode15s’ routine in Matlab 7.12 (The MathWorks, Natick, MA, USA), using the initial conditions and parameter values discussed in the next sections.
Table 3.
System of ODEs for each modelled species. Expressions for each v and μ term are found in table 2. For the HaCaT and C2C12 cases, the equations including the tagged TGF-β-induced pSmad1 species are gathered in the electronic supplementary material, table S2.
|
|
2.2. Initial conditions
Following the study of Chung et al. [28] and a survey of receptor numbers in a variety of cell types [46], we consider a total of 10 000 receptors of each type per cell, which we assume is evenly distributed between type I and type II receptors. We extend this assumption to all receptor species, yielding 5000 molecules per cell of RIIT, RIIB, RI1T, RI1B and RI2. It has been shown that these receptors are not distributed evenly between plasma membrane and endosomes. In fact, the distribution is heavily skewed towards internalized receptors, with approximately 90 per cent found within endosomes and 10 per cent remaining on the cell surface [16].
We use an initial value of 100 000 molecules of Smad2 and Smad4 per cell [29]. In the case of Smad1 proteins, we estimated a similar initial amount from comparative Western blots [14]. Smad proteins are also distributed non-uniformly between cytosol and nucleus with the majority remaining in the cytosol prior to induction. Approximately 15 per cent of Smad2 and 13 per cent of Smad4 is found in the nucleus in the non-induced cell [41]. We consider an initial nuclear distribution of 15 per cent for Smad1 proteins. Based on comparative Western blot data of Smad7 and Smad2 protein levels in HaCaT cells, we consider initially 39 000 Smad7 molecules per cell in this cell line [42]. In the BAEC and C2C12 cases, Smad7 has an initial value of zero. All other molecular species are initially set to zero. The full set of initial estimates for all the molecular species of the model is summarized in table 1.
Beginning with these initial estimates, we obtained the initial values of all the molecular species, shown in table 1, by allowing the system to reach a steady state prior to stimulation with the ligand.
2.3. Parameter estimation
Several of the parameters have been calculated from experimental data or determined from previous mathematical models. These parameters characterize the Smad2 channel dynamics in HaCaT cells upon treatment with TGF-β without considering the Smad7-mediated negative feedback loop. In order to add the Smad1 channel, we assume the same parameters apply to its Smad1-associated reactions. With the explicit inclusion of Smad7, we added two calculated parameter values (ksyn,S7 and kdeg,S7) and a set of seven estimated parameters (klip,1, klip,2, KA,1, KA,2, k20a,1T, k20a,1B and k20a,2) governing ligand-induced production of Smad7 and its affinity for the active ligand–receptor complex. The constitutive production value (ksyn,S7) was determined by solving the time-derivative for Smad7 (table 3) at steady state without ligand, ensuring that, under these conditions, the steady-state value of Smad7 remains at its initial concentration for each cell line. We used the results of an experimental degradation assay to calculate the constitutive degradation rate kdeg,S7 [47].
For the HaCaT cell line, we only optimized the estimated parameters associated with Smad7 dynamics, specifically klip,2, KA,2 and k20a,2. For the BAEC and C2C12 cell lines, we subject the parameters estimated in Chung et al. [28] to further optimization in order to account for variability between cell lines. The result is a set of parameters that is shared among the three cases (table 4) and another set with specific values for each cell line (table 5).
Table 4.
Literature and calculated values of model parameters shared among the three cell lines. For ksyn,S7, H denotes its value in the HaCaT case, while B/C identifies its value in the BAEC and C2C12 cases.
| parameter | description | value | unit | references |
|---|---|---|---|---|
| ksyn,RII | constitutive production of type II receptors | 8.00 | molecules min−1 | calculated in [28] |
| kdeg,RII | constitutive degradation of type II receptors | 2.78 × 10−2 | min−1 | [8] |
| ksyn,RI | constitutive production of type I receptors | 8.00 | molecules min−1 | calculated in [28] |
| kdeg,RI | constitutive degradation of type I receptors | 2.78 × 10−2 | min−1 | [8] |
| ksyn,RS | constitutive production of R-Smads | 2.74 × 101 | molecules min−1 | calculated in [28] |
| kdeg,RS | constitutive degradation of R-Smads | 6.46 × 10−4 | min−1 | calculated in [28] from [48] |
| ksyn,S4 | constitutive production of Smad4 | 5.00 × 101 | molecules min−1 | calculated in [28] |
| kdeg,S4 | constitutive degradation of Smad4 | 1.20 × 10−3 | min−1 | calculated in [28] from [49] |
| ksyn,S7 | constitutive production of Smad7 | H: 1.51 × 102; B/C: 0 | molecules min−1 | calculated here |
| kdeg,S7 | constitutive degradation of Smad7 | 3.88 × 10−3 | min−1 | calculated here from [47] |
| k1d | dissociation of ligand-type II receptor complex | 2.98 × 10−1 | min−1 | determined in [28] from [50] |
| k2d | dissociation of receptor complex | 2.98 × 10−1 | min−1 | determined in [28] from [51] |
| k5phos | phosphorylation of R-Smad | 4.48 × 104 | min−1 | determined in [28] from [52] |
| k6d | dissociation of cytosolic phospho-R-Smad–Smad4 complex | 1.46 × 103 | min−1 | determined in [28] from [53] |
| k8dp | dephosphorylation of nuclear phospho-R-Smad–Smad4 complex | 2.52 × 10−2 | min−1 | calculated in [28] from [54] |
| k11dp | dephosphorylation of phospho-R-Smad | 2.52 × 10−2 | min−1 | same as k8dp |
| k12imp | nuclear import of R-Smad | 1.62 × 10−1 | min−1 | [41] |
| k12exp | nuclear export of R-Smad | 3.48 × 10−1 | min−1 | [41] |
| k14exp | nuclear export of Smad4 | 1.74 × 10−1 | min−1 | [41] |
| k16deg | constitutive degradation of receptor complex | 2.78 × 10−2 | min−1 | [8] |
| k17rec | recycling of receptor complex | 3.95 × 10−2 | min−1 | as k18rec |
| k18rec | recycling of type II receptor | 3.95 × 10−2 | min−1 | calculated in [28] from [8] |
| k19rec | recycling of type I receptor | 3.95 × 10−2 | min−1 | as k18rec |
Table 5.
Estimated model parameters for the three cell lines. Values labelled ‘0 (fixed)’ were maintained at zero as we do not consider Smad1 channel dynamics in the optimization for the HaCaT case and we only induce Smad7 through the Smad1 channel in the BAEC case.
| parameter | description | HaCaT | BAEC | C2C12 | unit |
|---|---|---|---|---|---|
| k1a | association of ligand and type II receptor | 6.60 × 10−3* | 1.20 × 10−2 | 6.60 × 10−4 | molecules−1 min−1 |
| k2a | association of ligand–type II receptor and type I receptor | 6.60 × 10−3* | 1.44 × 10−3 | 3.76 × 10−2 | molecules−1 min−1 |
| k3int | internalization of receptor complex | 3.95 × 10−1* | 3.11 × 10−1 | 3.02 | min−1 |
| k4a | association of receptor complex and R-Smad | 1.50 × 10−4* | 2.12 × 10−4 | 1.92 × 10−5 | molecules−1 min−1 |
| k4d | dissociation of receptor complex and R-Smad | 9.71 × 10−1* | 9.61 | 9.68 | min−1 |
| k6a | association of cytosolic phospho-R-Smad and Smad4 | 6.00 × 10−3* | 8.94 × 10−3 | 5.31 × 10−2 | molecules−1 min−1 |
| k7imp | nuclear import of phospho-R-Smad–Smad4 complex | 8.10 × 10−1* | 2.70 × 10−1 | 7.52 | min−1 |
| k9d | dissociation of R-Smad–Smad4 complex | 1.01 × 10−1* | 9.60 × 10−1 | 1.01 | min−1 |
| k10a | association of nuclear phospho-R-Smad and Smad4 | 1.67 × 10−4* | 3.08 × 10−5 | 1.37 × 10−3 | molecules−1 min−1 |
| k10d | dissociation of nuclear phospho-R-Smad–Smad4 complex | 9.09 × 10−1* | 2.50 | 3.83 | min−1 |
| k13imp | nuclear import of phospho-R-Smad | 5.03 × 10−1* | 5.03 × 10−2 | 4.85 | min−1 |
| k14imp | nuclear import of Smad4 | 2.01 × 10−2* | 2.31 × 10−2 | 1.45 × 10−1 | min−1 |
| k15deg | constitutive degradation of nuclear phospho-R-Smad | 5.40 × 10−3* | 2.00 × 10−3 | 4.33 × 10−2 | min−1 |
| k18int | internalization of type II receptor | as k3int | as k3int | as k3int | min−1 |
| k19int | internalization of type I receptor | as k3int | as k3int | as k3int | min−1 |
| k20a,1T | association of Smad7 and C1T | 0 (fixed) | 9.38 × 10−4 | 8.72 × 10−4 | molecules−1 min−1 |
| k20a,1B | association of Smad7 and C1B | 0 (fixed) | 5.00 × 10−5 | 1.08 × 10−3 | molecules−1 min−1 |
| k20a,2 | association of Smad7 and C2 | 2.96 × 10−5 | 1.50 × 10−6 | 1.50 × 10−6 | molecules−1 min−1 |
| klip,1 | ligand-induced production of Smad7 through pS1S4n | 0 (fixed) | 4.26 × 102 | 1.77 × 102 | molecules min−1 |
| klip,2 | ligand-induced production of Smad7 through pS2S4n | 8.53 × 103 | 0 (fixed) | 5.54 × 102 | molecules min−1 |
| KA,1 | association constant pS1S4n with Smad7 promoter | 0 (fixed) | 7.22 × 10−5 | 5.35 × 10−5 | molecules−1 |
| KA,2 | association constant pS2S4n with Smad7 promoter | 1.03 × 10−6 | 0 (fixed) | 1.51 × 10−3 | molecules−1 |
*These parameter values for the HaCaT case were set to the estimated values in [28] and not optimized here.
To estimate the unknown parameters, we fit the simulation results to a series of experimental datasets for each cell line, encompassing the dynamics of different molecular species of both R-Smad channels, Smad4 and Smad7 proteins, as well as the effects of drugs, such as CHX. Unless otherwise stated, we collected the experimental data points by quantifying Western blot experiments using ImageJ 10.2 [55] and normalizing the time courses so the maximum concentration is 1. We define the objective function for minimization as the least-squares error between simulated and experimental data, which is given by
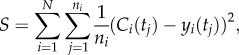 |
where Ci(tj) and yi(tj) denote the simulated and experimental relative concentration of the molecular species, respectively, at a time tj for a particular dataset i. We first sum over all ni time points of dataset i and normalize to this value, providing a means to compare between experiments with varying number of sample points. Finally, we sum over the N datasets for a given cell line. The experimental data used for parameter optimization consisted of (i) nuclear phosphorylated Smad2 (pSmad2) and Smad7 time courses upon TGF-β treatment [17,43] and cytosolic pSmad2, cytosolic Smad2 and nuclear Smad4 time courses upon treatment with TGF-β and CHX [56], for HaCaT cells; (ii) phosphorylated Smad1 (pSmad1) and pSmad2 time courses upon TGF-β treatment [31,44] and pSmad1 time courses upon BMP6 treatment [57], for BAEC cells, and (iii) pSmad1 and pSmad2 time courses upon TGF-β treatment and pSmad1 time courses upon BMP2 treatment, for C2C12 cells [14].
To determine the optimized set of parameters (table 5), we first used a simulated annealing method implemented by the ‘simulannealbnd’ routine, followed by the ‘patternsearch’ function in Matlab 7.12 (The MathWorks, Natick, MA, USA). This approach for minimization of the objective function first provides a global search in the parameter space and supplements it with an additional local minimization to further refine the parameter set. By doing so, we reduce the probability of terminating on a nearby local minima. The parameter space is defined by assigning to each parameter value a lower and upper bound of one order of magnitude below and above its initial value, respectively. Owing to lower degree of certainty with the Smad7 parameters (klip,1, klip,2, KA,1, KA,2, k20a,1T, k20a,1B and k20a,2), we increased their bounds by one additional order of magnitude in each direction. As a rough initial estimate for the ligand-induced production terms (klip,1 and klip,2), we used 1.51 × 102 molecules min−1, which corresponds to the calculated constitutive Smad7 production rate, ksyn,S7. Experimental association constants are available for R-Smad and Co-Smad binding to DNA, which provide the estimate of 1.70 × 10−5 molecules−1 for the values of KA,1 and KA,2 [58]. For the association rate constants (k20a,1T, k20a,1B and k20a,2), we assume their values will remain within a similar range as that of the ligand–receptor complex/R-Smad binding, defined by parameter k4a, and set them initially to 1.50 × 10−4 molecules−1 min−1, as estimated in Chung et al. [28].
2.4. Sensitivity analysis
In order to quantify the dependence of the behaviour of the system on the value of the individual parameters, we performed a sensitivity analysis for the model corresponding to the three cell lines. As a sensitivity metric, we examine the peak concentration of nuclear phosphorylated Smad2–Smad4 complexes after stimulation with 2 ng ml−1 of TGF-β for 10 h. The scaled sensitivity coefficients [59] are given by
where [pS2S4n]max is the maximum concentration in the nucleus of the pSmad2–Smad4 complex and ki denotes each of the parameters of the model. To approximate the partial derivative, we evaluate the model with one per cent perturbations of each parameter about its original value and calculate the finite central difference of the sensitivity metric [60].
3. Results
3.1. Model performance for the three different cell lines
For each cell line, we compare the simulation results of the model with the time-course experiments used for parameter optimization and examine the ability of the model to predict additional available experimental data not included in the optimization routine as a model validation step. We focus on the typical experimental conditions that measure the response of the system to a sudden change of the ligand (TGF-β or BMP2/BMP6) concentration from zero to a saturating value that is kept constant afterwards, unless otherwise specified.
3.1.1. Human keratinocyte cell line
The model parameters for the HaCaT case were optimized to a set of five time-course experiments upon TGF-β treatment. Comparison of the simulation results with the experimental data (figure 2a–e) shows a good agreement between the model and the time-course experiments in HaCaT cells used to estimate the parameters. In particular, the model accurately reproduces the rapid peak of nuclear pSmad2 within the first hour and tapering off over the subsequent 9 h observed in the experiments in response to a step function of the ligand at time zero (figure 2a). Figure 2b shows the effects on Smad7, which remains relatively static over the course of 10 h. The model also captures the slight decrease in Smad7 concentration immediately after TGF-β treatment, in qualitative agreement with the experimental behaviour [42], and then plateaus within 4 h.
Figure 2.
Results of model optimization (dashed lines) and predicted behaviour (solid lines) for HaCaT cells. Experimental data points (circles) were quantified from Western blots with ImageJ 10.2 [55], unless otherwise stated. (a–e) Optimization results (highlighted with grey shading). (a) Nuclear phosphorylated Smad2 with 2 ng ml−1 TGF-β. Experimental data are from [17]. (b) Smad7 with 10 ng ml−1 TGF-β. Experimental data are from [43]. (c) Cytosolic phosphorylated Smad2 with 2 ng ml−1 TGF-β and CHX. Experimental data are from [56] and quantified in [28]. (d) Cytosolic Smad2 with 2 ng ml−1 TGF-β and CHX. Experimental data are from [56]. (e) Nuclear Smad4 with 2 ng ml−1 TGF-β and CHX. Experimental data are from [56]. (f–i) Predicted behaviour. (f) Phosphorylated Smad2 with 2 ng ml−1 TGF-β and CHX. Experimental data are from [17]. (g) Phosphorylated Smad2 with cyclical 1 h treatments of 60 000 molecules per cell (1.25 ng ml−1) TGF-β. Experimental data and quantification are from [36]. (h) Ratio of phosphorylated Smad2 to Smad2 with pulse of 2 ng ml−1 TGF-β followed by SB431542. Experimental data and quantification were done in [54]. (i) Ratio of phosphorylated Smad2 to Smad2 with 2 ng ml−1 TGF-β. Experimental data and quantification were done in [54]. (Online version in colour.)
In addition, the model reproduces well the effects of a treatment with both TGF-β ligand and the inhibitory drug CHX (figure 2c–e). In the simulations, we consider the effects of CHX by setting all protein production rate constants (ksyn,RII, ksyn,RI, ksyn,RS, ksyn,S4, ksyn,S7, klip,1 and klip,2) to zero. This results in a highly transient cytosolic phosphorylated Smad2 response (figure 2c), which reaches pre-stimulus levels after 10 h. The model reproduces the experimentally observed decrease in cytosolic Smad2 (figure 2d) and the concomitant increase in nuclear Smad4 (figure 2e), which results mainly from the nuclear accumulation of pSmad2–Smad4 complexes. These results indicate that the model accurately captures the nucleocytoplasmic shuttling dynamics of the system.
To validate the model, we examined its ability to predict additional experimental data not used for parameter optimization [17,36,54]. Figure 2f–i displays the results of the validation step for the HaCaT case. The model accurately predicts the behaviour of additional molecular species, namely the total phosphorylated Smad2 (figure 2f), in response to a step input of TGF–β and treatment with CHX, which correspond to the same experimental conditions of figure 2c–e. Specifically, the model captures the sharp peak at 1 h and the quick descent towards pre-stimulus levels within the 5 h time course. In addition, we tested whether the model could reproduce different input functions for the ligand, the effects of new inhibitory drugs and the behaviour at longer time scales. In figure 2g, we show the simulation results for a cyclical treatment with TGF-β, which consists of a twice-repeated step input of TGF-β for 1 h and a wash of ligand for the following hour. The model captures the rapid increase in the total phosphorylated Smad2 levels after the first ligand treatment, the subsequent decrease upon ligand wash, and the inability of the system to relax to the pre-stimulus conditions before the second ligand treatment, which results in a weaker response, in agreement with the experimental results [36]. Furthermore, we considered the response of the system to a pulse input of TGF-β followed by treatment with SB431542, an inhibitor of receptor type I kinase activity. In the simulations, we consider the effects of this drug by setting the ALK5-mediated phosphorylation rate of Smad2 (k5phos) to zero. The model is again able to accurately predict the experimental results (figure 2h), specifically the rapid dephosphorylation of activated Smad2 species. Finally, in figure 2i, we compare the long-term model predictions upon a step input of TGF-β with the corresponding experimental data [54]. The model successfully captures the initial peak and decline, which reaches a steady-state value near half-maximal levels over the 25 h time course.
3.1.2. Bovine aortic endothelial cell line
The model parameters for the BAEC case were optimized to reproduce pSmad1 and pSmad2 experimental time courses upon treatment with TGF-β or BMP6 (figure 3a–c). The model captures the transient response of pSmad1 and the more sustained response of pSmad2 to a step input of the TGF-β ligand (figure 3a,b). In the case of BMP6 treatment, experiments display a rather different pSmad1 behaviour [57]. Figure 3c shows that the model reproduces the rapid peak and decline within the first 5 h after a step input of BMP6. Subsequently, the pSmad1 response stabilizes near 40 per cent of the maximal activation over the 25-h simulation.
Figure 3.
Results of model optimization (dashed lines) and predicted behaviour (solid lines) for BAEC cells. Experimental data points (circles) were quantified from Western blots with ImageJ 10.2 [55], unless otherwise stated. (a–c) Optimization results (highlighted with grey shading). (a) Phosphorylated Smad1 with 1 ng ml−1 TGF-β. Experimental data are from [31,44] and quantified in [31]. (b) Phosphorylated Smad2 with 1 ng ml−1 TGF-β. Experimental data are from [31,44] and quantified by [31]. (c) Phosphorylated Smad1 with 50 ng ml−1 BMP6. Experimental data are from [57]. (d,e) Predicted behaviour. Experimental data are from [44] and quantified in [31]. (d) Phosphorylated Smad1 with 1 ng ml−1 TGF-β and CHX. Experimental data are from [31]. (e) Phosphorylated Smad2 with 1 ng ml−1 TGF-β and CHX. Experimental data are from [31]. (Online version in colour.)
For model validation in BAEC cells, we examine the ability of the model to predict, without further parameter adjustment, activation of both R-Smad channels upon a step input of TGF-β with CHX treatment, which effectively eliminates Smad7 from the system (figure 3d,e). The model prediction reproduces the reversion of total phosphorylated Smad1 dynamics to a permanent response (figure 3d), similar to that of the total phosphorylated Smad2 (figure 3e), which is largely unchanged as compared to its behaviour without CHX. This behaviour results from active ligand–receptor complexes containing ALK1 being the primary target for Smad7-mediated degradation as opposed to those containing ALK5.
3.1.3. Mouse mesenchymal cell line
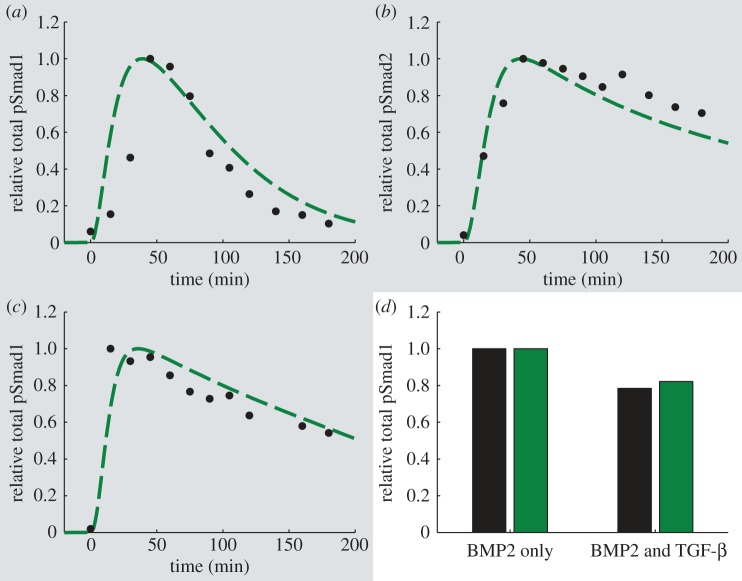
The model parameters for the C2C12 case were optimized to reproduce pSmad1 and pSmad2 experimental time courses upon treatment with TGF-β or BMP2 (figure 4a–c). As in the BAEC case, the model captures the transient total pSmad1 response (figure 4a) and the sustained pSmad2 response (figure 4b) over 3.3 h to a step input of the TGF-β ligand. In contrast to the behaviour observed upon TGF-β stimulation, BMP2 triggers a more sustained pSmad1 response (figure 4c).
Figure 4.
Results of model optimization (dashed lines) and predicted behaviour (solid lines) for C2C12 cells. Experimental data points (circles) were quantified from Western blots with ImageJ 10.2 [55], unless otherwise stated. (a–c) Optimization results (highlighted with grey shading). Experimental data are from [14]. (a) Phosphorylated Smad1 with 2 ng ml−1 TGF-β. (b) Phosphorylated Smad2 with 2 ng ml−1 TGF-β. (c) Phosphorylated Smad1 with 25 ng ml−1 BMP2. (d) Predicted behaviour. Experimental data (left bar) are from C3H 10T1/2 cells [61]. Simulations (right bar) display phosphorylated Smad1 concentration after 1 h of treatment with 1 nM (26 ng ml−1) of BMP2 or cotreatment with 1 nM (26 ng ml−1) of BMP2 and 100 pM (2.5 ng ml−1) TGF-β. (Online version in colour.)
To validate the model in the C2C12 case, we simulate the effects of costimulation with TGF-β and BMP2. Here, we compare the results of the model predictions to experimental data in C3H10T1/2 cells due to their qualitatively similar behaviour regarding the activation of transcription of BMP–responsive reporter genes with BREs to that of C2C12 cells [12,61]. The model accurately captures a diminished total phosphorylated Smad1 concentration upon treatment with both BMP2 and TGF-β when compared with BMP2 alone (figure 4d) indicating crosstalk between the two ligands. This effect may be attributed to the increased Smad7 production rate upon TGF-β treatment, which outcompetes any additional activation of the Smad1 channel, and Smad7–mediated targeting of active BMP–receptor complexes for degradation.
3.2. Cell line comparison
We examine how the model with the parameters for the three cell lines behaves under identical in silico conditions to better understand how their characteristic Smad7 dynamics affect the output. In order to compare the activation of both R-Smad channels, we chose to simulate the experimental conditions of figure 3a,b, which correspond to treatment with 1 ng ml−1 of TGF-β, for the three cell lines (figure 5a,b). To simulate the activation of the Smad1 channel for the HaCaT case, we set the values of klip,1, KA,1 and k20a,1T equal to those for the C2C12 case (table 5). Therefore, we consider saturating ligand concentration in all cases with the same type of stimulation.
Figure 5.
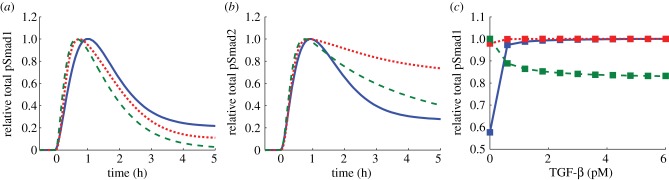
Simulated comparison of the model for the three cell types. In each panel, the results for the HaCaT, BAEC and C2C12 cases are shown as continuous, dotted and dashed lines, respectively. (a) Same simulation conditions as figure 3a. (b) Same simulation conditions as figure 3b. (c) Same simulation conditions as figure 4d over a range of TGF-β concentrations. BMP2 concentration is fixed at 1 nM (26 ng ml−1) as TGF-β increases from 0 to 6 pM (0.15 ng ml−1). Each symbol indicates the result of one simulation with lines drawn as a guide to the eye. (Online version in colour.)
Under these conditions, the three cell lines exhibit a highly transient pSmad1 response to TGF-β treatment (figure 5a). In contrast to the similar behaviour displayed for Smad1 activation, the model exhibits differences in the pSmad2 dynamics for the three cell lines (figure 5b). While pSmad2 shows a sustained response for the BAEC case, the HaCaT case produces a more transient response to TGF-β stimulation, with the behaviour for C2C12 cells falling between the two extreme cases.
In order to compare the effects of coupled signalling, we simulated the experimental conditions represented in figure 4d over a larger range of TGF-β concentrations (figure 5c). Specifically, the concentration of BMP2 is increased from 0 to 1 nM (26 ng ml−1) at time zero and the concentration of TGF-β is increased from 0 pM to specific values ranging from 0 to 6 pM (0.15 ng ml−1) and maintained constant afterwards. The pSmad1 response after 1 h of ligand treatment for the three different cases is shown in figure 5c. To simulate these conditions, for the HaCaT case, we set the value of the parameter k20a,1B to that of the C2C12 case and for the BAEC case we use its optimized value obtained for induction with BMP6 (table 5). Interestingly, the model for the three cases studied displays entirely distinct behaviour upon costimulation (figure 5c). The model for BAEC cells exhibits compensatory coupling between ligands since its response remains nearly constant as TGF-β levels are increased. For the HaCaT case, TGF-β treatment just adds to the system response. Interestingly, the system exhibits a diminished response as the concentration of TGF-β increases for the C2C12 case, in agreement with the experimental results of figure 4d.
The results shown in figure 5 thus illustrate how the determinant of the qualitative differences of the signalling responses from different cell types is the type of feedback regulation. Specifically, in all cases TGF-β activates both Smad1 and Smad2 channels. The duration and shape of the response, however, depends on the cell type. In HaCaT cells (solid lines in figure 5), pre-stimulus Smad7 is high and induction of Smad7 expression by the Smad2 channel does not contribute significantly to the feedback. The fact that there is no effective feedback implies that there is no substantial coupling between BMP and TGF-β signalling. In BAEC cells (dotted lines in figure 5), the Smad1 channel induces Smad7 expression, which later on shuts down the Smad1 channel and slightly decreases the Smad2 channel. Addition of TGF-β proportionately adds both Smad7 and pSmad1 to the system, resulting in compensatory coupling between ligands. In C2C12 cells (dashed lines in figure 5), the Smad2 channel induces Smad7 expression, which shuts down both Smad1 and Smad2 channels. In this case, Smad1 activation by TGF-β does not compensate the increase in Smad7, which results in decreased pSmad1. Therefore, the type of Smad7-mediated feedback controls not only the shape of the response but also the crosstalking between TGF-β and BMP pathways.
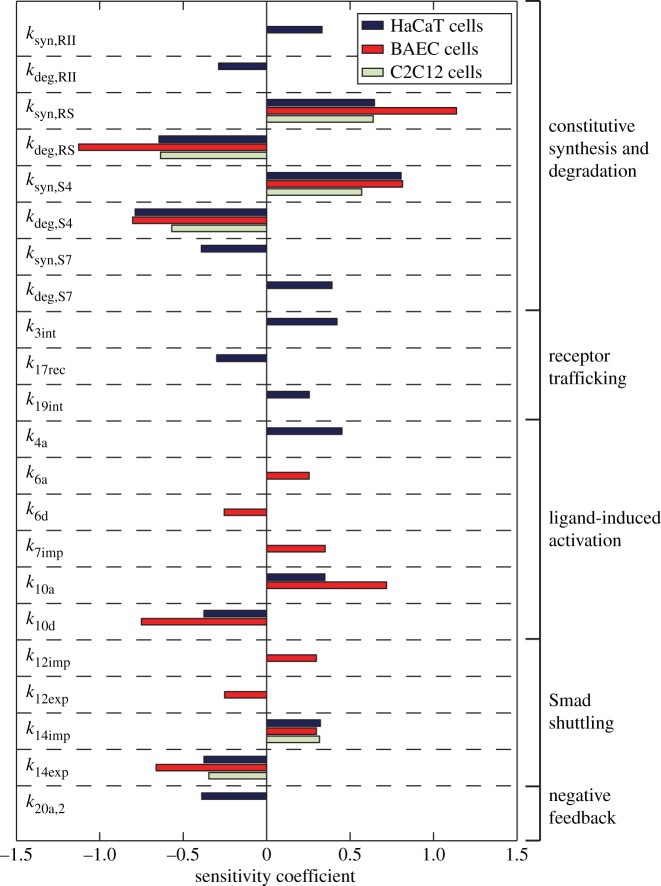
3.3. Sensitivity analysis
Finally, we assessed the sensitivity of the behaviour of the system on the specific value of the individual parameters by performing a sensitivity analysis for the model corresponding to the three cell lines, as described in §2.4. Specifically, we focused on the maximum value of the concentration of the transcriptionally active nuclear pSmad2–Smad4 molecular species. We calculated the sensitivity coefficients for all the parameters of the model and those with absolute values larger than 0.25 are shown in figure 6. This analysis reveals a high dependence of the system behaviour on the production and degradation rates of components shared between the two R-Smad channels, mainly those of the R-Smads and Smad4. In all the cases, the response is sensitive to the synthesis and degradation of both R-Smad and Smad4 as well as to the nucleocytoplasmic shuttling of Smad4. Because of the Smad7 feedback loop, the response of BAEC and C2C12 cell lines does not depend on the synthesis and degradation of the receptors. In the case of HaCaT cells, such feedback loop is basically absent and the amplitude of the response is sensitive to receptor production and degradation.
Figure 6.
Sensitivity analysis for the three cell lines. Only the parameters with an absolute value of the scaled sensitivity coefficient above 0.25 are shown. (Online version in colour.)
4. Discussion
The TGF-β signal transduction pathway consists of a complex network of interacting modules that are regulated through several layers of control mechanisms. This complexity in regulation is responsible for diverse types of signalling dynamics that are highly dependent on both the environmental context and the specific cell type. We have shown that our computational model accurately reproduces experimental time courses for HaCaT, BAEC and C2C12 cell lines in both optimization and validation steps. The main characteristic of the model is that it keeps the same type of receptor and R-Smad/Co-Smad dynamics among the three cell lines, but the dynamics is differentially controlled in each case by varying Smad7 expression and its receptor targeting behaviour. As a result, it captures the distinct signalling patterns of the Smad1/5/8 and Smad2/3 channels, including their activation by different ligands of the TGF-β superfamily.
To further understand how the negative feedback properties of Smad7-dependent receptor downregulation affect the signalling dynamics, we compared the model for the three cell lines (figure 5) and characterized both the properties of single-ligand response as well as the two-ligand coupling effects. Interestingly, while the model for the BAEC and C2C12 cell lines show similar phosphorylated R-Smad time courses for a single ligand, their response to costimulation by TGF-β and BMP varies significantly. Since Smad7 is fully controlled by Smad1 activation in the BAEC case, addition of TGF-β proportionately adds both Smad7 and pSmad1 to the system, resulting in compensatory coupling between ligands. The C2C12 case exhibits a crosstalk between R-Smad channels, as the sustained pSmad2 signal and associated Smad7 expression reduces the pSmad1 output once TGF-β is added to the system, decreasing the BMP signal. The HaCaT case behaves in an opposite fashion, wherein TGF-β positively regulates pSmad1 output, adding to the BMP signal. This is largely a result of the high initial Smad7 concentration in this cell line. Even though both ligands induce Smad7 expression, its level is sufficiently high to nearly saturate the system. Consequently, TGF-β adds to the pool of pSmad1 with little impact on negative feedback.
The effects of the different types of crosstalk between TGF-β and BMP in the intracellular signalling dynamics of each cell type can be summarized as follows. In HaCaT cells, since there is no Smad7 negative feedback, TGF-β adds to the BMP signal through the Smad1 channel. In BAEC cells, TGF-β does not impact substantially BMP signal through Smad1 because the increase in Smad7 compensates the increase in pSmad1. In C2C12 cells, adding TGF-β practically shuts down BMP signalling because the effects of increasing Smad7 are much stronger than the increase in pSmad1.
Our results show that crosstalk provides an additional layer of regulation for HaCaT and C2C12 cell lines in determining the signal response upon costimulation with TGF-β and BMP by either cooperating to enhance the signal or inhibiting the response of the other when both ligands are present simultaneously. Indeed, both ligands are key regulators of development and differentiation in epithelial and mesenchymal cells, in some cases eliciting distinct phenotypic responses. For instance, TGF-β has been shown to both stimulate and inhibit myoblast differentiation at different stages in the process, whereas BMP has an inhibitory effect by diverging differentiation towards an osteoblast fate [2,62]. Our results provide further insight into the downstream signalling dynamics and mechanistic details that may give rise to these behaviours through cooperation or inhibition among TGF-β and BMP, providing additional modulation of pSmad1 and pSmad2 activation and regulating processes that respond to both ligands.
In all cases, Smad7 is a key component of the negative feedback loop responsible for the distinct behaviour of the different cell types considered. The use of detailed protein synthesis kinetics for Smad7 in HaCaT cells, even though sufficiently large amounts of endogenous Smad7 exist, shows that the feedback loop in this case does not substantially affect the dynamics, unlike the cases for BAEC and C2C12 cell lines. There are also other feedback mechanisms, such as the typical autocrine production of TGF-β ligand [63], which was not considered here because it does not affect the signalling dynamics under saturating ligand concentrations.
We performed a sensitivity analysis that provided key insights into the robustness of each negative regulatory pattern. Overall, the amplitude of the nuclear pSmad2–Smad4 response in all cell lines is sensitive to parameter perturbation related to the synthesis and degradation of both R-Smad and Smad4 as well as to the nucleocytoplasmic shuttling of Smad4. Ligand–receptor trafficking dynamics has been previously identified as a key determinant property of the system behaviour. In this case, mathematical models of receptor-level behaviour were capable of accurately reproducing distinct experimental R-Smad activation dynamics for different cell lines [8,34]. In our analysis, we have found that the amplitude of the pSmad2–Smad4 response in the nucleus to TGF-β depends on the receptor production and degradation only for HaCaT cell lines. According to previous studies [8,34], the shape and duration of the pSmad2 response in HaCaT cells, in contrast to its amplitude, are completely determined by the type of post-stimulus degradation of the receptors and do not depend on the absolute number of the receptors. Therefore, differences in the number of receptors will affect the extent of crosstalk but not whether TGF-β adds to, compensates or suppresses BMP signalling.
The high sensitivity of the HaCaT cell line to receptor production and degradation may provide insight into the progression of cancer in epithelial cell lines. Specifically, a number of cancer types, including those found in the breast, lung and prostate, are characterized with lost expression of the TGF-β type I and type II receptors [5]. Epithelial cells in these tissues may share TGF-β signalling characteristics with HaCaT cells, wherein those exhibiting high sensitivity to mutated receptor expression would be more likely to display aberrant signalling patterns and a resulting pathological phenotype upon mutation. The results of the sensitivity analysis are consistent with experimental data in cancer cells derived from a number of tissues in identifying receptor synthesis and degradation as sensitive processes that may result in altered cell behaviour when mutated [5]. The sensitivity analysis results may therefore be used as a tool for further investigation of mutated components in this signalling pathway, and how they may affect progression of disease in a variety of tissues.
Our mathematical model thus provides novel insights into the underlying machinery of the TGF–β signal transduction pathway. By incorporating negative feedback, both R-Smad channels and stimulation by multiple ligands, we are able to better understand how multiple cell types exhibit unique signalling patterns under identical environmental conditions. This provides an important step towards fully mapping the complex network of signal transduction in the TGF-β superfamily.
Acknowledgements
This work was supported by the University of California, Davis (to L.S.).
References
- 1.Massagué J. 1998. TGF-β signal transduction. Annu. Rev. Biochem. 67, 753–791 10.1146/annurev.biochem.67.1.753 (doi:10.1146/annurev.biochem.67.1.753) [DOI] [PubMed] [Google Scholar]
- 2.Derynck R, Miyazono K. 2008. The TGF-β family. Cold Spring Harbor monograph series, p. 1114 Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press [Google Scholar]
- 3.Gordon KJ, Blobe GC. 2008. Role of transforming growth factor-β superfamily signaling pathways in human disease. Biochim. Biophys. Acta 1782, 197–228 10.1016/j.bbadis.2008.01.006 (doi:10.1016/j.bbadis.2008.01.006) [DOI] [PubMed] [Google Scholar]
- 4.Massagué J. 2008. TGFβ in cancer. Cell 134, 215–230 10.1016/j.cell.2008.07.001 (doi:10.1016/j.cell.2008.07.001) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Levy L, Hill CS. 2006. Alterations in components of the TGF-β superfamily signaling pathways in human cancer. Cytokine Growth Factor Rev. 17, 41–58 10.1016/j.cytogfr.2005.09.009 (doi:10.1016/j.cytogfr.2005.09.009) [DOI] [PubMed] [Google Scholar]
- 6.Wrana JL, Attisano L, Wieser R, Ventura F, Massagué J. 1994. Mechanism of activation of the TGF-β receptor. Nature 370, 341–347 10.1038/370341a0 (doi:10.1038/370341a0) [DOI] [PubMed] [Google Scholar]
- 7.Shi Y, Massagué J. 2003. Mechanisms of TGF-β signaling from cell membrane to the nucleus. Cell 113, 685–700 10.1016/S0092-8674(03)00432-X (doi:10.1016/S0092-8674(03)00432-X) [DOI] [PubMed] [Google Scholar]
- 8.Vilar JMG, Jansen R, Sander C. 2006. Signal processing in the TGF-β superfamily ligand–receptor network. PLoS Comput. Biol. 2, e3. 10.1371/journal.pcbi.0020003 (doi:10.1371/journal.pcbi.0020003) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Feng X-H, Derynck R. 2005. Specificity and versatility in TGF-β signaling through Smads. Annu. Rev. Cell Dev. Biol. 21, 659–693 10.1146/annurev.cellbio.21.022404.142018 (doi:10.1146/annurev.cellbio.21.022404.142018) [DOI] [PubMed] [Google Scholar]
- 10.Goumans M-J, et al. 2002. Balancing the activation state of the endothelium via two distinct TGF-β type I receptors. EMBO J. 21, 1743–1753 10.1093/emboj/21.7.1743 (doi:10.1093/emboj/21.7.1743) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bharathy S, Xie W, Yingling JM, Reiss M. 2008. Cancer-associated transforming growth factor β type II receptor gene mutant causes activation of bone morphogenic protein-Smads and invasive phenotype. Cancer Res. 68, 1656–1666 10.1158/0008-5472.CAN-07-5089 (doi:10.1158/0008-5472.CAN-07-5089) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Daly AC, Randall RA, Hill CS. 2008. Transforming growth factor β-induced Smad1/5 phosphorylation in epithelial cells is mediated by novel receptor complexes and is essential for anchorage-independent growth. Mol. Cell Biol. 28, 6889–6902 10.1128/MCB.01192-08 (doi:10.1128/MCB.01192-08) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Liu IM, Schilling SH, Knouse KA, Choy L, Derynck R, Wang X-F. 2009. TGFβ-stimulated Smad1/5 phosphorylation requires the ALK5 L45 loop and mediates the pro-migratory TGFβ switch. EMBO J. 28, 88–98 10.1038/emboj.2008.266 (doi:10.1038/emboj.2008.266) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wrighton KH, Lin X, Yu PB, Feng X-H. 2009. Transforming growth factor β can stimulate Smad1 phosphorylation independently of bone morphogenic protein receptors. J. Biol. Chem. 284, 9755–9763 10.1074/jbc.M809223200 (doi:10.1074/jbc.M809223200) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Itoh S, ten Dijke P. 2007. Negative regulation of TGF-β receptor/Smad signal transduction. Curr. Opin. Cell Biol. 19, 176–184 10.1016/j.ceb.2007.02.015 (doi:10.1016/j.ceb.2007.02.015) [DOI] [PubMed] [Google Scholar]
- 16.Di Guglielmo GM, Le Roy C, Goodfellow AF, Wrana JL. 2003. Distinct endocytic pathways regulate TGF-β receptor signalling and turnover. Nat. Cell Biol. 5, 410–421 10.1038/ncb975 (doi:10.1038/ncb975) [DOI] [PubMed] [Google Scholar]
- 17.Inman GJ, Nicolás FJ, Hill CS. 2002. Nucleocytoplasmic shuttling of Smads 2, 3, and 4 permits sensing of TGF-β receptor activity. Mol. Cell 10, 283–294 10.1016/S1097-2765(02)00585-3 (doi:10.1016/S1097-2765(02)00585-3) [DOI] [PubMed] [Google Scholar]
- 18.Mitchell H, et al. 2004. Ligand-dependent and -independent transforming growth factor-β receptor recycling regulated by clathrin-mediated endocytosis and Rab11. Mol. Biol. Cell 15, 4166–4178 10.1091/mbc.E04-03-0245 (doi:10.1091/mbc.E04-03-0245) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Afrakhte M, Morén A, Jossan S, Itoh S, Sampath K, Westermark B, Heldin C-H, Heldin N-E, ten Dijke P. 1998. Induction of inhibitory Smad6 and Smad7 mRNA by TGF-β family members. Biochem. Biophys. Res. Commun. 249, 505–511 10.1006/bbrc.1998.9170 (doi:10.1006/bbrc.1998.9170) [DOI] [PubMed] [Google Scholar]
- 20.Takase M, Imamura T, Sampath TK, Takeda K, Ichijo H, Miyazono K, Kawabata M. 1998. Induction of Smad6 mRNA by bone morphogenetic proteins. Biochem. Biophys. Res. Commun. 244, 26–29 10.1006/bbrc.1998.8200 (doi:10.1006/bbrc.1998.8200) [DOI] [PubMed] [Google Scholar]
- 21.Hata A, Lagna G, Massagué J, Hemmati-Brivanlou A. 1998. Smad6 inhibits BMP/Smad1 signaling by specifically competing with the Smad4 tumor suppressor. Genes Dev. 12, 186–197 10.1101/gad.12.2.186 (doi:10.1101/gad.12.2.186) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Goto K, Kamiya Y, Imamura T, Miyazono K, Miyazawa K. 2007. Selective inhibitory effects of Smad6 on bone morphogenetic protein type I receptors. J. Biol. Chem. 282, 20 603–20 611 10.1074/jbc.M702100200 (doi:10.1074/jbc.M702100200) [DOI] [PubMed] [Google Scholar]
- 23.Nakao A, et al. 1997. Identification of Smad7, a TGFβ-inducible antagonist of TGF-β signalling. Nature 389, 631–635 10.1038/39369 (doi:10.1038/39369) [DOI] [PubMed] [Google Scholar]
- 24.Kavsak P, Rasmussen RK, Causing CG, Bonni S, Zhu H, Thomsen GH, Wrana JL. 2000. Smad7 binds to Smurf2 to form an E3 ubiquitin ligase that targets the TGFβ receptor for degradation. Mol. Cell 6, 1365–1375 10.1016/S1097-2765(00)00134-9 (doi:10.1016/S1097-2765(00)00134-9) [DOI] [PubMed] [Google Scholar]
- 25.Ebisawa T, et al. 2001. Smurf1 interacts with transforming growth factor-β type I receptor through Smad7 and induces receptor degradation. J. Biol. Chem. 276, 12 477–12 480 10.1074/jbc.C100008200 (doi:10.1074/jbc.C100008200) [DOI] [PubMed] [Google Scholar]
- 26.Zi Z, Chapnick DA, Liu X. 2012. Dynamics of TGF-β/Smad signaling. FEBS Lett. 586, 1921–1928 10.1016/j.febslet.2012.03.063 (doi:10.1016/j.febslet.2012.03.063) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wegner K, et al. 2012. Dynamics and feedback loops in the transforming growth factor β signaling pathway. Biophys. Chem. 162, 22–34 10.1016/j.bpc.2011.12.003 (doi:10.1016/j.bpc.2011.12.003) [DOI] [PubMed] [Google Scholar]
- 28.Chung S-W, Miles FL, Sikes RA, Cooper CR, Farach-Carson MC, Ogunnaike BA. 2009. Quantitative modeling and analysis of the transforming growth factor β signaling pathway. Biophys. J. 96, 1733–1750 10.1016/j.bpj.2008.11.050 (doi:10.1016/j.bpj.2008.11.050) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Clarke DC, Betterton MD, Liu X. 2006. Systems theory of Smad signalling. IEE Proc.-Syst. Biol. 153, 412–424 10.1049/ip-syb:20050055 (doi:10.1049/ip-syb:20050055) [DOI] [PubMed] [Google Scholar]
- 30.Chung SW, Cooper CR, Farach-Carson MC, Ogunnaike BA. 2012. A control engineering approach to understanding the TGF-β paradox in cancer. J. R. Soc. Interface 9, 1389–1397 10.1098/rsif.2011.0799 (doi:10.1098/rsif.2011.0799) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Melke P, Jasson H, Pardali E, ten Dijke P, Peterson C. 2006. A rate equation approach to elucidate the kinetics and robustness of the TGF-β pathway. Biophys. J. 91, 4368–4380 10.1529/biophysj.105.080408 (doi:10.1529/biophysj.105.080408) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Paulsen M, Legewie S, Eils R, Karaulanov E, Niehrs C. 2011. Negative feedback in the bone morphogenetic protein 4 (BMP4) synexpression group governs its dynamic signaling range and canalizes development. Proc. Natl Acad. Sci. USA 108, 10 202–10 207 10.1073/pnas.1100179108 (doi:10.1073/pnas.1100179108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Schmierer B, Tournier AL, Bates PA, Hill CS. 2008. Mathematical modeling identifies Smad nucleocytoplasmic shuttling as a dynamic signal-interpreting system. Proc. Natl Acad. Sci. USA 105, 6608–6613 10.1073/pnas.0710134105 (doi:10.1073/pnas.0710134105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Vilar JMG, Saiz L. 2011. Trafficking coordinate description of intracellular transport control of signaling networks. Biophys. J. 101, 2315–2323 10.1016/j.bpj.2011.09.035 (doi:10.1016/j.bpj.2011.09.035) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zi Z, Klipp E. 2007. Constraint-based modeling and kinetic analysis of the Smad dependent TGF-β signaling pathway. PLoS ONE 2, e936. 10.1371/journal.pone.0000936 (doi:10.1371/journal.pone.0000936) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zi Z, et al. 2011. Quantitative analysis of transient and sustained transforming growth factor-β signaling dynamics. Mol. Syst. Biol. 7, 492. 10.1038/msb.2011.22 (doi:10.1038/msb.2011.22) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Celliere G, Fengos G, Hervac M, Iber D. 2011. Plasticity of TGF-β signaling. BMC Syst. Biol. 5, 184. 10.1186/1752-0509-5-184 (doi:10.1186/1752-0509-5-184) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Goumans M-J, Valdimarsdottir G, Itoh S, Lebrin F, Larsson J, Mummery C, Karlsson S, ten Dijke P. 2003. Activin receptor-like kinase (ALK)1 is an antagonistic mediator of lateral TGFβ/ALK5 signaling. Mol. Cell 12, 817–828 10.1016/S1097-2765(03)00386-1 (doi:10.1016/S1097-2765(03)00386-1) [DOI] [PubMed] [Google Scholar]
- 39.Lowery JW, de Caestecker M. 2010. BMP signaling in vascular development and disease. Cytokine Growth Factor Rev. 21, 287–298 10.1016/j.cytogfr.2010.06.001 (doi:10.1016/j.cytogfr.2010.06.001) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Nicolás FJ, et al. 2004. Analysis of Smad nucleocytoplasmic shuttling in living cells. J. Cell Sci. 117, 4113–4125 10.1242/jcs.01289 (doi:10.1242/jcs.01289) [DOI] [PubMed] [Google Scholar]
- 41.Schmierer B, Hill CS. 2005. Kinetic analysis of Smad nucleocytoplasmic shuttling reveals a mechanism for transforming growth factor β-dependent nuclear accumulation of Smads. Mol. Cell Biol. 25, 9845–9858 10.1128/MCB.25.22.9845-9858.2005 (doi:10.1128/MCB.25.22.9845-9858.2005) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Nicolás FJ, Hill CS. 2003. Attenuation of the TGF-β-Smad signaling pathway in pancreatic tumor cells confers resistance to TGF-β-induced growth arrest. Oncogene 22, 3698–3711 10.1038/sj.onc.1206420 (doi:10.1038/sj.onc.1206420) [DOI] [PubMed] [Google Scholar]
- 43.Edlund S, Lee SY, Grimsby S, Zhang S, Aspenström P, Heldin C-H, Landström M. 2005. Interaction between Smad7 and β-catenin: importance for transforming growth factor β-induced apoptosis. Mol. Cell Biol. 25, 1475–1488 10.1128/MCB.25.4.1475-1488.2005 (doi:10.1128/MCB.25.4.1475-1488.2005) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Valdimarsdottir G, Goumans M-J, Itoh F, Itoh S, Heldin C-H, ten Dijke P. 2006. Smad7 and protein phosphatase 1α are critical determinants in the duration of TGF-β/ALK1 signaling in endothelial cells. BMC Cell Biol. 7 10.1186/1471-2121-7-16 (doi:10.1186/1471-2121-7-16) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Yuzawa H, Koinuma D, Maeda S, Yamamoto K, Miyazawa K, Imamura T. 2009. Arkadia represses the expression of myoblast differentiation markers through degradation of Ski and the Ski-bound Smad complex in C2C12 myoblasts. Bone 44, 53–60 10.1016/j.bone.2008.09.013 (doi:10.1016/j.bone.2008.09.013) [DOI] [PubMed] [Google Scholar]
- 46.Wakefield LM, et al. 1987. Distribution and modulation of the cellular receptor for transforming growth factor-β. J. Cell Biol. 105, 965–975 10.1083/jcb.105.2.965 (doi:10.1083/jcb.105.2.965) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Liu W, et al. 2006. Axin is a scaffold protein in TGF-β signaling that promotes degradation of Smad7 by Arkadia. EMBO J. 25, 1646–1658 10.1038/sj.emboj.7601057 (doi:10.1038/sj.emboj.7601057) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lo RS, Massagué J. 1999. Ubiquitin-dependent degradation of TGF-β-activated Smad2. Nat. Cell Biol. 1, 472–478 10.1038/70258 (doi:10.1038/70258) [DOI] [PubMed] [Google Scholar]
- 49.Wan M, et al. 2002. Jab1 antagonizes TGF-β signaling by inducing Smad4 degradation. EMBO Rep. 3, 171–176 10.1093/embo-reports/kvf024 (doi:10.1093/embo-reports/kvf024) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Segarini PR, Rosen DM, Seyedin SM. 1989. Binding of transforming growth factor-β to cell surface proteins varies with cell type. Mol. Endocrinol. 3, 261–272 10.1210/mend-3-2-261 (doi:10.1210/mend-3-2-261) [DOI] [PubMed] [Google Scholar]
- 51.Goetschy J-F, et al. 1996. The unglycosylated extracellular domain of type-II receptor for transforming growth factor-β. A novel assay for characterizing ligand affinity and specificity. Eur. J. Biochem. 241, 355–362 10.1111/j.1432-1033.1996.00355.x (doi:10.1111/j.1432-1033.1996.00355.x) [DOI] [PubMed] [Google Scholar]
- 52.Peng S-B, et al. 2005. Kinetic characterization of novel pyrazole TGF-β receptor I kinase inhibitors and their blockade of the epithelial-mesenchymal transition. Biochemistry 44, 2293–2304 10.1021/bi048851x (doi:10.1021/bi048851x) [DOI] [PubMed] [Google Scholar]
- 53.Funaba M, Mathews LS. 2000. Identification and characterization of constitutively active Smad2 mutants: evaluation of formation of Smad complex and subcellular distribution. Mol. Endocrinol. 14, 1583–1591 10.1210/me.14.10.1583 (doi:10.1210/me.14.10.1583) [DOI] [PubMed] [Google Scholar]
- 54.Lin X, et al. 2006. PPM1A functions as a Smad phosphatase to terminate TGFβ signaling. Cell 125, 915–928 10.1016/j.cell.2006.03.044 (doi:10.1016/j.cell.2006.03.044) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Abramoff MD, Magalhaes PJ, Ram SJ. 2004. Image processing with ImageJ. Biophoton. Int. 11, 36–42 [Google Scholar]
- 56.Pierreux CE, Nicolás FJ, Hill CS. 2000. Transforming growth factor β-independent shuttling of Smad4 between the cytoplasm and nucleus. Mol. Cell Biol. 20, 9041–9054 10.1128/MCB.20.23.9041-9054.2000 (doi:10.1128/MCB.20.23.9041-9054.2000) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Valdimarsdottir G, Goumans MJ, Rosendahl A, Brugman M, Itoh S, Lebrin F, Sideras P, ten Dijke P. 2002. Stimulation of Id1 expression by bone morphogenetic protein is sufficient and necessary for bone morphogenetic protein-induced activation of endothelial cells. Circulation 106, 2263–2270 10.1161/01.CIR.0000033830.36431.46 (doi:10.1161/01.CIR.0000033830.36431.46) [DOI] [PubMed] [Google Scholar]
- 58.Shi Y, Wang Y-F, Jayaraman L, Yang H, Massaguac J, Pavletich NP. 1998. Crystal structure of a Smad MH1 domain bound to DNA: insights on DNA binding in TGF-β signaling. Cell 94, 585–594 10.1016/S0092-8674(00)81600-1 (doi:10.1016/S0092-8674(00)81600-1) [DOI] [PubMed] [Google Scholar]
- 59.Varma A, Morbidelli M, Wu H. 1999. Parametric sensitivity in chemical systems. Cambridge series in chemical engineering, p. 342 Cambridge, UK: Cambridge University Press [Google Scholar]
- 60.Press WH, Teukolsky SA, Vetterling WT, Flannery BP. 2007. Numerical recipes: the art of scientific computing, p. 1235 New York, NY: Cambridge University Press [Google Scholar]
- 61.Rebbapragada A, Benchabane H, Wrana JL, Celeste AJ, Attisano L. 2003. Myostatin signals through a transforming growth factor β-like signaling pathway to block adipogenesis. Mol. Cell Biol. 23, 7230–7242 10.1128/MCB.23.20.7230-7242.2003 (doi:10.1128/MCB.23.20.7230-7242.2003) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Derynck R, Akhurst RJ. 2007. Differentiation plasticity regulated by TGF-β family proteins in development and disease. Nat. Cell Biol. 9, 1000–1004 10.1038/ncb434 (doi:10.1038/ncb434) [DOI] [PubMed] [Google Scholar]
- 63.Miyazono K. 2000. Positive and negative regulation of TGF-β signaling. J. Cell Sci. 113, 1101–1109 [DOI] [PubMed] [Google Scholar]