Table 1. Estimates of the parameters used in our dynamic HIV-FGS model (Figure 1).
| Variable | Meaning (units) | Prior distribution [ref] | Posterior distribution: median (95% CI) |

|
Annual growth rate rural population | 0.034 [29] | N/A |
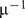
|
Duration of sexual activity (year-1) | 1/35 | N/A |
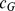
|
Enhanced HIV transmission due to FGS | Uniform(0,20) | 5.9 (3.8–9.1) |
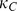
|
Probability of FGS given childhood infection | Uniform(0.33,0.75) [8] | 0.47 (0.38–0.56) |
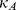
|
Probability of acquiring FGS during adulthood | Uniform(0.005,0.05) | 0.008 (0.006–0.009) |
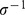
|
Duration of HIV infection (years) | Uniform(7.5,12.5) [33, 48] | 10.7 (8.1–12.1) |
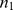
|
Number of sex acts in partnerships per year for high-risk group | Uniform(15,150) [48] | 128 (95–148) |
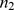
|
Number of sex acts in partnerships per year for low-risk group | Uniform(50,248) [48] | 69 (28–137) |
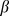
|
HIV transmission rate per sex act | Uniform(0.0006,0.004) [23], [39] | 0.0022 (0.0009–0.003) |

|
Mixing between sexual risk groups | Uniform(0.2,0.9) [49] | 0.44 (0.22–0.62) |
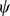
|
Extent to which males determine the pattern of sexual partnerships formation | Uniform(0.2,0.8) [48] | 0.67 (0.50–0.78) |
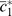
|
Initial partner change rate: women (year-1) | Triangular(0.66,2.4,0.9) [48] | 1.27 (0.7–2.2) |
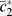
|
Initial partner change rate: men (year-1) | Triangular(1.1,3,1.2) [48] | 1.9 (1.2–2.8) |
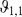
|
Fraction of women in high-risk group | Uniform(0.05,0.6) [48] | 0.20 (0.15–0.24) |
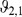
|
Fraction of men in high-risk group | Uniform(0.10,0.75) [48] | 0.34 (0.22–0.49) |
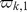
|
Relative rate of partner change: high-risk versus low-risk group | Uniform(1,100) [48] | 10.7 (2.5–21.8) |
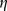
|
Reduction rate of partner change | Uniform(1,50) | 6.5 (3.5–9.0) |
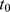
|
Year HIV epidemic starts | Uniform(1978,1985) [48,50] | 1981 (1980–1982) |
These parameter estimates produced the best fit of our dynamic model to epidemiological data for HIV and FGS prevalence and co-infection among rural Zimbabwean women [3], [7]. The dynamic model was fit to these data using a Markov Chain Monte Carlo method, which allowed us to calculate distributions of possible values for each of these parameters. We present here the mean of these distributions and their associated 95% credible intervals. The Brooks-Gelman-Rubin (BGR) method was used to monitor convergence of iterative simulations. Convergence was achieved when the upper limit of the credible interval of the BGR diagnostic statistic for a given parameter <1.2 [51].
