A penalized likelihood approach to estimate within-household contact networks from egocentric data

Summary

Acute infectious diseases are transmitted over networks of social contacts. Epidemic models are used to predict the spread of emergent pathogens and compare intervention strategies. Many of these models assume equal probability of contact within mixing groups (homes, schools, etc.), but little work has inferred the actual contact network, which may influence epidemic estimates. We develop a penalized likelihood method to infer contact networks within households, a key area for disease transmission. Using egocentric surveys of contact behavior in Belgium, we estimate within-household contact networks for six different age compositions. Our estimates show dependency in contact behavior and vary substantively by age composition, with fewer contacts occurring in older households. Our results are relevant for epidemic models used to make policy recommendations.

1. Introduction

Acute infectious diseases, such as influenza, spread through networks of face-to-face social contacts. When a new strain of influenza virus emerges, a variety of epidemic models are used to estimate key epidemic parameters, simulate and predict epidemic spread, and compare intervention strategies. The majority of these models are based on the simplistic “random mixing” assumption regarding social contact behavior. Under this assumption, people contact each other with equal probability within mixing groups (homes, schools, workplaces, etc.), but no other social contact structure is modeled. For example, the large scale agent-based models in Eubank et al. (2004), Germann et al. (2006), Ferguson et al. (2006), and Halloran et al. (2008) assume random mixing within homes, grades and/or schools, workplaces and workgroups, and communities. Furthermore, random mixing within households is used in models estimating secondary attack rates within households. See Longini et al. (1988); Halloran et al. (2007); Yang et al. (2007) and Yang et al. (2009). Classical models to estimate the basic reproductive number R₀ assume random mixing with age-specific contact probabilities (e.g. Diekmann et al. (1990) and Anderson and May (1991)). Because these models use infection or symptom data but not contact data, age differentials in their transmission rate estimates result both from differential infectiousness and susceptibility by age, as well as differences in contact behavior by age. An understanding of the contact network is essential to disentangle the effects of biology and behavior.

Researchers have demonstrated that network structure can result in different epidemic predictions than random mixing. Keeling and Eames (2005) reviewed idealized types of networks which have been used to approximate the contact network, and compared the epidemic curve from simulated disease transmission over various network types to that obtained over random mixing. Keeling and Eames (2005) and Miller (2009) showed that clustering affects the course of the epidemic and explored how the effect varies by clustering level and for different types of networks. Researchers are actively involved in estimating properties of contact networks and integrating survey-based network information into epidemic estimation models. Wallinga et al. (2006) supplemented infectious disease data with social contact data to improve estimates of age-specific transmission parameters. They demonstrated that their model, which integrates the age-specific contact rates and mixing patterns, improves model fit over random mixing. Ogunjimi et al. (2009) extended the methodology in Wallinga et al. (2006) and applied it to the Belgian data from the POLYMOD study, a multi-country European survey of contact behavior, which we analyze in this paper. In addition, Goeyvaerts et al. (2011) combined social contact data with serological data for human parovirus B19 (PVB19) and found evidence for age-specific waning of PVB19 immunity in four of five European countries they analyzed.

Households are known to be a primary component of the disease transmission process, but relatively little work has been done to estimate contact networks within households. As mentioned previously, most household models assume random mixing within households. Britton and O’Neill (2002) developed a Bayesian method to estimate the infection rate, mean of the infection period, and probability of social contact, and assumed this probability is equal for all pairs; i.e. random mixing. Demiris and O’Neill (2005) developed inference for infection rates and imputed the contact graph, assuming random mixing within and between groups. Potter et al. (2011) is the first paper we know of that develops inference for within-household contact networks from egocentric data. They applied their parametric model to the same data set we analyze here.

We contribute to this area by developing a method to estimate small contact networks from survey data and applying it to model networks of household contacts using the Belgian POLYMOD data. We estimate the probability distributions for household networks of size four of various age compositions in Belgium. We compare the results to a random mixing scenario, and we investigate the effect of age composition on the contact network. Our method requires fewer assumptions about contact behavior than that of Potter et al. (2011).

Our method also contributes to the field of social network methodology by inferring the probability distribution for complete networks from partially observed network data. We represent a network graphically by using nodes to represent social actors and ties to represent contacts between people, and mathematically by a square matrix Y where Y_ij = 1 if persons i and j make contact and Y_ij = 0 if not. One standard class of network models, exponential family random graph models (ERGMs) represent global network structure as a function of local social behavior (Strauss and Ikeda, 1990). Inference for ERGMs was developed assuming observation of the complete network; Handcock and Gile (2010) developed inference for ERGMs from partially observed networks. Such estimation assumes that the ERGM is correctly specified: that the features of the network are indeed captured by the network statistics included in the model. For exploratory work to describe an unknown network or get an initial sense of which statistics will be relevant, a nonparametric estimation procedure of the probability distribution would be very useful.

The network data we analyze is egocentric: randomly sampled respondents were interviewed about their contacts to other members, but they did not report on contacts between other members. They reported attributes of people they contacted but not identities. Egocentric data is a commonly available network data type. It contains information about assortative mixing (the tendency to contact others with similar attributes) and the degree distribution, where the degree is the number of contacts a person makes. Egocentric data does not include information about transitivity or other higher-level network structures. Network inference for egocentric data may be performed by assuming contacts occur independently conditional on individual-level attributes (as described in Koehly et al. (2004)), or by imposing a dependence structure. We ascertain the identities of household contacts by matching the age of the contacted member to the household age roster. Thus, our data set contains more information than a random egocentric sample, permitting us to estimate dependence in contact behavior. The networks we analyze are size four with a single respondent per household, so each respondent reported half of the network (three of six possible contacts). Reports from different respondents in multiple households therefore contain a fair amount of information to characterize the probability distribution of the network.

This paper is organized as follows. In section 2, we describe the POLYMOD study. In section 3.1 we present a nonparametric maximum likelihood method to estimate the probability distribution of a small contact network of fixed size from egocentric data. With the constraint of assuming that children are exchangeable and adults are exchangeable, this method can be used to estimate the nonparametric MLE of the contact network distribution for a large data set, but in smaller data sets such as ours, the parameters are not identifiable. We resolve this through a penalized likelihood approach, described in section 3.2. Our penalty imposes a mathematical preference for distributions representing networks where contacts between members occur independently of each other. In section 3.4 we describe a simulation study to assess predictive performance of our method in large data sets. We estimate the probability distribution of within-household contact networks for households of size four of six different age compositions in Belgium. Estimates for three household types are presented and compared in section 4.1; we also compare the estimates to random mixing. Results from the three other household compositions are in the supplementary material. Results from the simulation study are presented in section 4.2. In section 5 we discuss our findings and the performance of our method.

2. The POLYMOD Data

The POLYMOD survey was administered in eight European countries in 2006 and contains detailed diaries of contact behavior during a day. We analyze the Belgian POLYMOD data. Mossong et al. (2008) analyzed the POLYMOD data set and compare contact patterns between countries, and Hens et al. (2009) analyzed the Belgian POLYMOD data using association rules and classification trees. In Belgium, random digit dialing was used to obtain consent, and sampling weights ensure that the three main regions of Belgium were represented (Flemish, Walloon, and Brussels). Children were oversampled because they are key transmitters of infections. Data were collected from 750 respondents during March–May of 2006, with one respondent per household. Each respondent was mailed a paper diary and was assigned two randomly selected days, one weekday and one weekend day. To ensure that observations are independent, we analyze the first day reported by each respondent. Approximately half of respondents (381 of 750) filled out the first day of their diary during the two-week Easter holiday period (April 3–17), during which schools were closed. For each assigned day, respondents were instructed to record information about all social contacts from 5 a.m. till 5 a.m. the next morning. A contact was defined to be a two-way conversation of at least three words in the same location and/or a physical contact. The age and sex of the person contacted were recorded, as well as attributes of the contact itself including frequency (daily or almost daily, once or twice a week, etc.), and location (home, work, school, leisure, transport, or other). Respondents also listed demographic information of self and their households, including ages of all household members.

Respondents did not report whether people contacted were household members, and our aim is to estimate the contact networks between household members. We assume that contacts were to household members if they occurred “at home”, were reported as “daily or almost daily”, and if their age matches one of the reported ages of household members. For each household we observe a partial contact network: we have information on ties between the respondent and all other members, but not on contacts between other members. Our data is egocentric, but with the assumptions we have made, includes the identity of the alters.

We develop a method to model the contact network for households of fixed size and age composition and apply this method to households of size four in the Belgian POLYMOD data. We classify members into the following age categories which we expect to exhibit different contact behavior: 0–5, 6–11, 12–18, 19–35, and 36+. Table 1 shows the distribution of age compositions of households of size four in our data set.

Table 1.

Age composition of households of size four in the Belgian POLYMOD data set.

Age Category					Number of Respondents
0–5	6–11	12–18	19–35	36+
0	0	0	0	4	1
0	0	0	1	3	1
0	0	0	2	2	35
0	0	0	3	1	1
0	0	0	4	0	1
0	0	1	1	2	23
0	0	1	2	1	1
0	0	2	0	2	40
0	0	3	0	1	2
0	1	0	0	3	1
0	1	0	1	2	1
0	1	1	1	1	2
0	1	2	0	1	1
0	1	1	0	2	17
0	1	2	0	1	1
0	2	0	0	2	16
0	2	0	1	1	8
0	2	0	2	0	4
1	0	1	0	2	1
1	1	0	0	2	6
1	1	0	1	1	8
1	1	0	2	0	12
2	0	0	0	2	2
2	0	0	1	1	12
2	0	0	2	0	16

Table 2 shows the six household composition types we analyze in this paper. In households with small children, we collapsed the two adult age groups to obtain adequate sample sizes for each group. Based on our understanding of social norms, we expect each of these households to exhibit different contact patterns.

Table 2.

Household composition types analyzed in this paper

Household Type	Child 1	Child 2	Parent 1	Parent 2	n
Type 1	0–5	0–5	19+	19+	30
Type 2	0–5	6–11	19+	19+	26
Type 3	6–11	6–11	19+	19+	28
Type 4	12–18	12–18	36+	36+	40
Type 5	12–18	19–35	36+	36+	23
Type 6	19–35	19–35	36+	36+	35

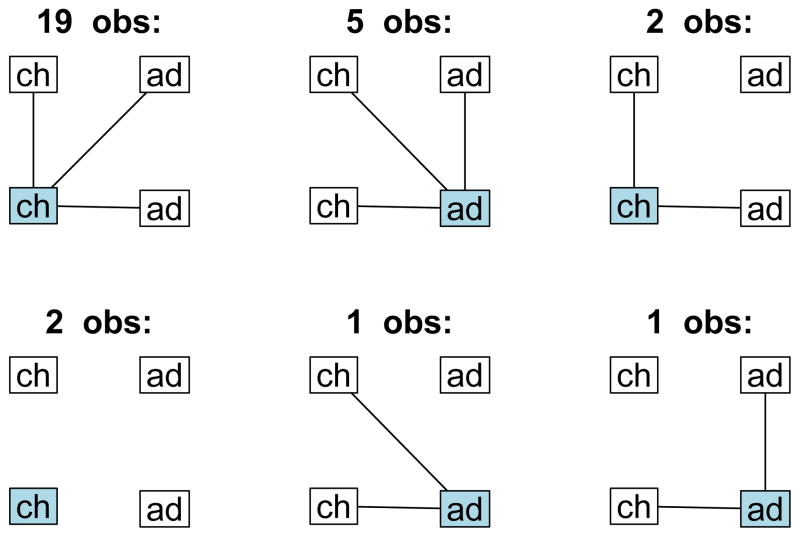
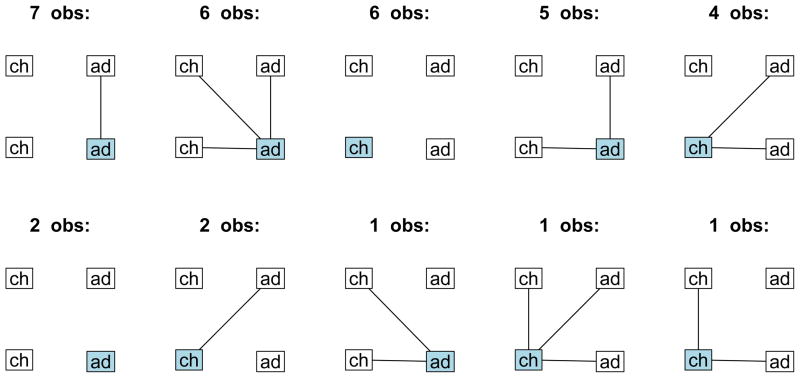
Figure 1 shows our observed data for households with two 0–5 year olds and two 19+ year olds. The respondent is marked in blue, and lines indicate reported contacts. Because of our structurally missing data, contact status on dyads excluding the respondent is not observed. In order to display the observed data concisely, we assume that the two children are exchangeable and the two adults are exchangeable. However, we do not make this assumption in our model. Figure 2 shows observed data for households with two young adults and two older adults. Density of contact is substantially smaller than it is in the younger household type, and we see more diverse reporting patterns in this type of household.

Fig. 1.

Subset of observed data: households with two 0–5 year olds and two 19+ year olds; respondent in blue. Lines indicate reported contact. Labels are: ch=child, ad=adult.

Fig. 2.

Subset of observed data: households with two 19–35 year olds and two 36+ year olds; respondent in blue. Lines indicate reported contact. Labels are: ch=child, ad=adult.

3. Methodology

3.1. A Nonparametric Approach

We develop a technique for estimating the probability distribution of a small household network of fixed size from egocentric data. The method makes no assumptions about the similarity in behavior between household members. Here we discuss its application to a household of size four with two 0–5 year olds, and two 19+ year olds. Contacts as defined by the survey are symmetric, so there are $\left(\begin{array}{c}4\\ 2\end{array}\right)=6$ possible contacts in each household. We will use vector notation to represent the network, since it is more compact than matrix notation and easier to display our results. We represent the household network by a 6-vector, z, where each element of z represents a possible contact between two members. The total number of possible contact networks for a household of this age composition is 2⁶ = 64.

For each surveyed household, only three of the six possible contacts are observed. Let y denote the observed network, a 6-vector where three elements are missing.

We first express the likelihood of the data in the most general form, which allows for any parametrization. Let Y_i denote the vector representing the network reported by respondent i, and let n be the number of respondents. Let R_i denote the respondent type of respondent i (younger child, older child, female adult, or male adult). We denote the probability of network k by p_θ(k). Sampling probabilities of the various respondent types are denoted p_ψ (R_i = r_i). The separate parametrization of the network probability distribution and the sampling probabilities is justified by the sampling design: the process of selecting respondents was independent of the within-household contact network.

Each observation includes the respondent type which determines which dyads are observed, as well as the values of the observed dyads. We can compute the likelihood contribution of one respondent by summing the probabilities of all complete networks which are consistent with the partially observed network. The joint probability mass function of observed respondent type and observed dyadic data is thus

$$P(Y_i=y_i,R_i=r_i\mid \theta ,\psi )=\left(\sum _{k=1}^{64}{p}_{\theta }(k)1_{[\text{k},\text{i}]}\right)p_{\psi }(R_i=r_i),$$

where

$$1_{[\text{k},\text{i}]}=\{\begin{array}{ll}1\hfill & \text{if}\text{partially}\text{observed}\text{network}{y}_i\text{is}\text{consistent}\text{with}\text{network}\text{k}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$

The joint likelihood function of θ and ψ is thus:

$$L(\theta ,\psi \mid Y_i=y_i,R_i=r_i)=\left(\sum _{k=1}^{64}{p}_{\theta }(k)1_{[\text{k},\text{i}]}\right)p_{\psi }(R_i=r_i)$$

We are concerned with estimation of θ, and it’s clear that the score equations for θ will be free of ψ. Thus we can restrict our attention to the likelihood for θ alone:

$$L(\theta \mid Y_i=y_i,R_i=r_i)\propto \sum _{k=1}^{64}{p}_{\theta }(k)1_{[\text{k},\text{i}]}$$

We begin by describing a nonparametric approach, in which we assume no functional relationship between the probabilities of different networks; that is p_θ (k) ≡ p_k, where p is a vector in 64-space. This approach makes no assumptions about the similarity of contact behavior between household members. The likelihood of p is thus

$$L(\mathbf{p}\mid Y_1=y_1,\dots Y_n=y_n,\mathbf{R}=\mathbf{r})\propto \prod _{i=1}^n\sum _{k=1}^{64}{p}_k{1}_{[\text{k},\text{i}]}$$

We would like to obtain the maximum likelihood estimate (MLE), but we have an identifiability problem. The likelihood function includes 63 free parameters (64 which sum to one). The number of possible distinct data configurations is 32, as there are four types of respondents (so four missingness patterns) and 2³ = 8 possible reports from each respondent. Estimation will only be possible if we can restrict our parameter space to have 32 or fewer free parameters. One way to reduce the identifiability problem is to assume that the two children are exchangeable and the two adults are exchangeable. This reduces the dimension of the parameter space to 27 (28 parameters which sum to one). However, we feel this approach is sensible only when the two children fall into the same age group, so the method could not be applied to households with two children in different age groups. In addition, we expect the female and male adults in the household to behave differently. Moreover, we still do not have enough observed data points to accurately estimate the parameters. Although there are 27 types of data configurations, only nine of these possibilities are observed in our data set with two 0–5 year olds and two 19+ year olds. Our data does not contain enough information to estimate all the parameters in the likelihood.

3.2. A Penalized Likelihood Approach

To resolve the identifiability problem, we use a penalized likelihood approach, also referred to as regularization (Kim and Sanderson, 2008). We add to the likelihood a smoothing penalty which imposes a preference for probability distributions of networks in which contacts occur independently, a common assumption in epidemic models.

When we assume independence, we have only six parameters, the probabilities of contact between each pair of household members. We’ll denote them by η, a vector with six elements. We estimate η_j with the MLE of the binomial distribution:

$${\widehat{\eta }}_j=\frac{{\sum }_{i=1}^n{1}_{[d_{j,i}=1]}}{{\sum }_{i=1}^n{1}_{[d_{j,i}=0]}+{\sum }_{i=1}^n{1}_{[d_{j,i}=1]}},$$

where d_j,i = 1 if respondent i reports contact on dyad j, d_j,i = 0 if non-contact is reported, and d_j,i is not observed for all respondents due to the structurally missing data.

When we assume independence, the probabilities of each network are a deterministic function of η:

$$\text{P}(\mathbf{Z}=\mathbf{z})=\prod _{j=1}^6{\eta }_j^{z_j}{(1-{\eta }_j)}^{1-z_j}$$

Let p_k,ind denote the probability of network k under the independence assumption as described above, while (as mentioned previously) p_k denotes the unknown probability of network k with no independence restriction. We use the squared Hellinger distance to compare these distributions, so our penalized likelihood function with the independence penalty is:

$$PL(\mathbf{p},\lambda )=\text{log}L(\mathbf{p}\mid y_1,\dots y_n))-\lambda \left(\frac{1}{2}\sum _{k=1}^{64}{(\sqrt{p_{k,\mathit{ind}}}-\sqrt{p_k})}^2\right),$$

The tuning parameter, λ, controls the degree of smoothness that is applied to the likelihood. When λ = 0, the estimates are completely informed by the data without any parametric assumptions. As λ → ∞, the penalty dominates the formula, and our estimate converges to the independence estimate.

The choice of penalty may influence the results. We tried two other penalty functions and compared their effect on the results. We tried a penalty which imposes a preference for distributions in which networks differing on a single dyad have similar probabilities, defined by:

$$PL(\mathbf{p},\lambda )=\text{log}L(\mathbf{p}\mid y_1,\dots y_n))-\lambda \sum _{i,j}{(p_i-p_j)}^2{1}_{[\text{networks}i\text{and}j\text{differ}\text{on}\text{a}\text{single}\text{dyad}]}$$

As expected, this penalty smooths the probability parameters, but we found the extent of smoothing to result in unrealistic estimates of probability distributions. Results are included in the supplementary material.

We also tried a penalty which imposes a preference for probability distributions in which the two children are exchangeable and the two adults are exchangeable. We define the penalized log likelihood function with this penalty as follows:

$$PL(\mathbf{p},\lambda )=\text{log}L(\mathbf{p}\mid y_1,\dots y_n))-\lambda \sum _{i,j}{(p_i-p_j)}^2{1}_{[\text{networks}i\text{and}j\text{isomorphic}\text{under}\text{exchangeability}]}$$

We found that this penalty does not contribute enough information to resolve our identifiability problem. There are a total of 28 unique networks when accounting for isomorphisms under exchangeability, but our subset of households with two 0–5 year olds and two 19+ year olds contains only nine types of partially observed networks. Thus, even with a very large tuning parameter, the exchangeability penalty is insufficient to identify the parameters.

To select the tuning parameter, we performed leave-one-out cross-validation (CV) as described by Hastie et al. (2008). We implemented the procedure as follows:

We performed the following algorithm for λ on a grid ranging from 0 to 40:

1. Omit one data point, maximize the penalized likelihood for the remaining n − 1.

2. for the (penalized) MLE, compute the non-penalized likelihood for the omitted point.

3. Repeat (1) and (2) n times, so that each data point is omitted for one iteration.

4. Compute the mean of the non-penalized likelihood over all n iterations.

We selected the value of λ which maximized the mean of the non-penalized likelihood. This is an extension of cross-validation from a prediction setting to a likelihood setting, in which we replace minimization of mean squared error with maximization of the likelihood.

An alternate way to define the optimal tuning parameter is the smallest λ which results in an identifiable penalized likelihood. According to Catchpole and Morgan (1997), we can measure the identifiability of a likelihood equation by the rank of the Hessian matrix at the MLE, for exponential families. We tried this approach, but the large amount of noise we observed in the relationship between the rank of the Hessian and the tuning parameter made it difficult to precisely identify the cutoff. We estimated the rank of the true Hessian by computing the rank of the observed Hessian with the qr function in R. We expect the relationship between the rank of the true Hessian and the tuning parameter to be monotonically increasing, but we found a non-monotone, noisy relationship. We believe the problem arises from limited precision in our rank computation method. The Hessian is computed by qr based on the number of eigenvalues of the matrix which are zero, so depends on the precision with which R measures the magnitude of the eigenvalues, several of which are very close to zero. Computing the rank of the true (rather than observed) 63 by 63 Hessian matrix is a non-trivial problem and is beyond the scope of this paper. Because this approach was unsuccessful, we present only results using the cross-validation-selected λ.

We maximized the penalized likelihood function, subject to the constraint that the probabilities sum to 1 and all lie between 0 and 1, to obtain the penalized maximum likelihood estimate. We performed optimization in R version 2.9.2 (R Development Core Team, 2009), with the optim function and the BFGS method (Broyden, 1970).

We believe that in most cases the penalized likelihood maximum is unique, but it is not clear that uniqueness is guaranteed for all data sets. In the unpenalized setting, the uniqueness of the maximum likelihood estimate is not guaranteed for a fixed sample size, except in the case of exponential families under certain conditions (Lehmann and Casella, 1998). As λ → ∞, the penalized likelihood approaches a product of binomial random variables, whose likelihood has a unique maximum. When λ is too small to ensure identifiability, we expect multiple maxima. When λ is large enough to ensure identifiability, we expect a unique maxima for most data sets. We found the results from the optimization procedure to vary with the starting value provided, because for some starting values the routine converged to a local rather than global maximum. We report results based on a uniform starting probability distribution, which we found to consistently produce the largest maximum. In exploring appropriate starting values, we did not find evidence for multiple global maxima. However, it is not clear to us that a unique maximum is guaranteed for our penalized likelihood, and it is possible that certain data sets may produce multiple maxima.

Unpenalized estimates were computed by maximizing the unpenalized likelihood using the optim function in R. Since the parameter is not identifiable, multiple maxima may exist. One example in households with two 0–5 year olds and two 19+ year olds, is that the data do not contain information to distinguish between the following two networks: (0 1 0 0 0 1) and (0 1 1 0 0 1). Denoting unobserved dyads by ., these networks are consistent with the following observed data points: (0 . . 0 0 .), (0 . . 0 0 .), and (. 1 . 0 . 1), none of which give evidence favoring one of the true networks over the other. The maximum returned by the optimization routine placed equal probability on the two networks, but distributing that probability mass differently between the two does not shift the likelihood value. We report the maximum returned by optim.

The classical likelihood-based method to estimate uncertainty by inverting the Fisher information matrix does not apply when the likelihood is penalized (Lehmann and Casella, 1998). The classical approach also fails for the unpenalized likelihood since it requires an identifiable parameter. Instead we compute standard errors for the penalized and unpenalized maximum likelihood estimates through a nonparametric bootstrap, as described by Efron and Tibshirani (1993). We used 500 bootstrap resamples. For the penalized likelihood bootstrap, we fixed the tuning parameter to the one selected on the original data set. For comparison purposes, we also computed estimates and confidence intervals (also using the nonparametric bootstrap) for the independence model described above.

3.3. Model Comparison

We performed a hypothesis test to assess whether the penalized likelihood model differs significantly from an independence model. A classical likelihood ratio test assesses whether the parameter of a larger model falls inside a constrained subspace of the parameter space, or outside of the subspace, so testing whether releasing the constraints improves model fit. In our case, the subspace is the set of parameter vector satisfying the independence assumption:

$$\left\{\mathbf{p}:\exists {\eta }_1,\dots ,{\eta }_6\in [0,1]\text{such}\text{that}{p}_k\equiv \text{P}(\mathbf{Z}=\mathbf{z})=\prod _{j=1}^6{\eta }_j^{z_j}{(1-{\eta }_j)}^{1-z_j}\right\}$$

We want to test:

• H₀ : The true parameter is associated with an independence model.

• H_A : The true parameter is not associated with an independence model.

The classical LRT will not work in our setting, because we are not working in a likelihood framework; we’re using a semi-parametric method. The classical theorems do not apply. We are not aware of an analogous approach for penalized likelihood. Instead we used a bootstrap to approximate the distribution of the LRT statistic, as follows.

1. We simulated data sets with the same size and respondent composition as ours from the independence estimates (H₀).

2. For each data set, we performed cross validation to compute the optimal lambda.

3. For the simulated data set, we estimated the penalized MLE, and the penalized MLE when parameters are constrained to the subspace associated only with independence models.

4. We computed the difference in log likelihoods, the test statistic: value of penalized log likelihood at its maximum - value of penalized log likelihood with independence constraint at its maximum.

5. We repeated (1–4) 300 times.

We computed the p-value: the probability that the statistic under H₀ is greater than or equal to the observed statistic. When calculating the likelihood ratio test results, we found that about 9% of the 300 evaluations resulted in a negative likelihood ratio test statistic, likely due to convergence of the algorithm to a local maximum. We discarded these evaluations from analysis.

3.4. Simulation Study

We performed a simulation study to assess predictive performance of our method as follows. We used the unpenalized MLE for households with two 0–5 year olds and two 19+ year olds to generate 200 samples of size 30, the observed sample size for this household composition. Next, we randomly assigned respondent status to one person in each simulated household using the observed frequency of different respondent types: six younger children, 17 elder children, four female adults, and three male adults. We recoded dyads which would not be reported by the respondent as missing. The penalized likelihood approach was then used to estimate the multinomial probability vector for a grid of λ-values ranging from 0 to 50 by steps of 0.5. Based on the estimated probability vector we computed the mean average squared error and its bias-variance decomposition using the following definitions:

$$\begin{array}{l}\text{MSE}(\lambda )=\frac{1}{64}\sum _{k=1}^{64}\frac{1}{200}\sum _{s=1}^{200}{\left({\widehat{p}}_{sk}(\lambda )-p_{\text{true},k}\right)}^2,\\ \text{Bias}(\lambda )=\frac{1}{64}\sum _{k=1}^{64}\left({\overline{\widehat{p}}}_k(\lambda )-p_{\text{true},k}\right),\\ \text{Variance}(\lambda )=\frac{1}{64}\sum _{k=1}^{64}\frac{1}{200}\sum _{s=1}^{200}{\left({\widehat{p}}_{sk}(\lambda )-{\overline{\widehat{p}}}_k(\lambda )\right)}^2\end{array}$$

We repeated this procedure using the unpenalized MLE from a different household type: households with two 12–18 and two 36+ year olds, using the observed sample size (40) and respondent frequency (8 younger children, 20 elder children, 4 female adults, and 8 male adults) for this household composition. We performed the simulation study with the independence penalty and the adjacency penalty. For the adjacency penalty, we performed simulations for λ-values ranging from 0 to 10 by steps of 0.25, because the trends in bias, MSE, and variance are more visible in this range.

Whereas the cross-entropy and the Hellinger distance are more appropriate to measure the difference between probabilities, we chose to use the MSE because of its bias-variance decomposition. Due to the limited available data, the MSE was calculated on the same data that was used to estimate the CV. Future studies with larger sample sizes would allow using a second dataset to evaluate the MSE more properly.

4. Results

4.1. Penalized likelihood estimates

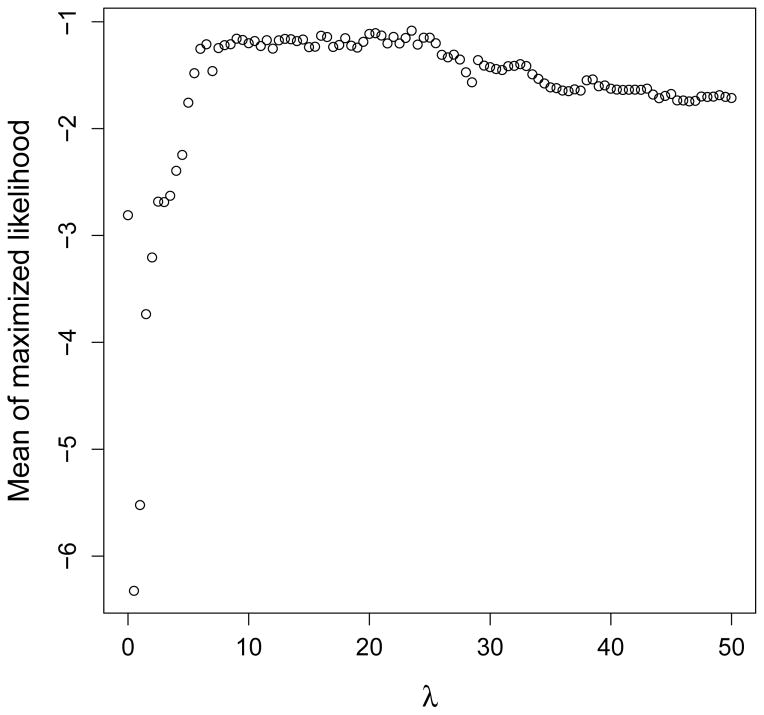
Figure 3 shows the relationship between the tuning parameter and the mean of the likelihood from the cross-validation procedure for households with two 0–5 year olds and two 19+ year olds. The maximum occurs at λ = 23.5. As expected, the curve is concave down, although there is more noise than expected. Other household compositions showed less noise in the relationship; those plots are included in the supplementary material.

Fig. 3.

Cross-validation results for the independence penalty

Table 3 shows estimates for the probability distribution of the network from three methods: unpenalized MLE, independence MLE, and penalized MLE. To ease comparison of estimates between the three methods, we display the estimates in adjacent columns, followed by confidence intervals in adjacent columns. We omit from display networks whose probability estimates under all three models were less than 0.02. The complete network (in which all contacts occur) receives a high probability estimate by all three methods. As we would expect, the penalized likelihood estimates generally lie between the unpenalized estimates and the independence estimates. The second network in the table receives non-negligible probability mass under both the penalized and unpenalized methods, but zero probability under the independence model. This indicates that the data give support for this network, but the restrictions of the independence model are too strong to detect that support. The smoothing imposed by the penalty does not remove the preference for this network.

Table 3.

Estimated probability distribution of contact network for households with two 0–5 year olds and two 19+ year olds. Dyad-independent, penalized likelihood (CV-selected λ = 23.5), and unpenalized likelihood estimates are shown.

Contact network						Estimate			95% C.I.
c1-c2	c1-m	c1-d	c2-m	c2-d	m-d	MLE	pen.MLE	indep.	MLE	pen.MLE	indep.
0	1	0	0	0	1	0.04	0	0	[0, 0.10]	[0, 0]	[0, 0]
0	1	1	0	0	1	0.04	0.06	0	[0, 0.10]	[0, 0.15]	[0, 0.02]
0	1	1	1	1	1	0	0.01	0.05	[0, 0]	[0, 0.01]	[0, 0.10]
1	1	1	0	0	1	0	0	0.02	[0, 0]	[0, 0.02]	[0, 0.07]
1	1	1	0	1	0	0	0.01	0.02	[0, 0]	[0, 0.07]	[0, 0.08]
1	1	1	0	1	1	0.07	0.08	0.13	[0, 0.21]	[0.01, 0.21]	[0.03, 0.23]
1	1	1	1	0	0	0	0.01	0.02	[0, 0]	[0, 0.03]	[0, 0.06]
1	1	1	1	0	1	0.05	0.06	0.1	[0, 0.17]	[0, 0.17]	[0, 0.18]
1	1	1	1	1	0	0.14	0.12	0.09	[0, 0.48]	[0, 0.42]	[0, 0.33]
1	1	1	1	1	1	0.65	0.65	0.54	[0.30, 0.89]	[0.35, 0.88]	[0.26, 0.83]

Table 4 shows the estimates for households with two 12–18 year olds and two 36+ year olds. Because the CV-selected λ = 199 was much larger for this household, the penalized likelihood estimates are closer to the independence estimates. The bootstrap-based likelihood ratio test results showed a significant departure from independence for the households with two 0–5 year olds and two 19+ year olds (p-value< 0.01) whereas no significant departure from independence was found for the households with two 12–18 year olds and two 36+ year olds (p-value 0.24). These results are in line with the values of λ estimated for these two household types. Tables of estimates for the other four household composition types are included in the supplementary material. The values of λ estimated by cross-validation varied from 20 to 199. Small values of λ suggest that the data set contributes a fair amount of predictive power, so less smoothing is necessary. Larger values of λ show the need for more smoothing.

Table 4.

Estimated probability distribution of contact network for households with two 12–18 year olds and two 36+ year olds. Dyad-independent, penalized likelihood (CV-selected λ = 199), and unpenalized likelihood estimates are shown.

Contact network						Estimate			95% C.I.
c1-c2	c1-m	c1-d	c2-m	c2-d	m-d	MLE	pen.MLE	indep.	MLE	pen.MLE	indep.
0	0	0	1	1	0	0.07	0.01	0	[0, 0.17]	[0, 0.03]	[0, 0.02]
0	0	1	0	0	1	0.05	0	0	[0, 0.16]	[0, 0.02]	[0, 0]
0	0	1	1	1	1	0.03	0.04	0.03	[0, 0.16]	[0, 0.09]	[0, 0.09]
0	1	0	0	0	0	0.06	0	0	[0, 0.15]	[0, 0.02]	[0, 0]
0	1	1	1	1	1	0	0.03	0.06	[0, 0]	[0.01, 0.10]	[0.02, 0.12]
1	0	0	1	1	1	0	0.02	0.04	[0, 0]	[0, 0.06]	[0, 0.08]
1	0	1	0	0	1	0.07	0.01	0	[0, 0.17]	[0, 0.02]	[0, 0.01]
1	0	1	1	1	0	0.04	0.04	0.04	[0, 0.23]	[0, 0.12]	[0, 0.11]
1	0	1	1	1	1	0	0.12	0.11	[0, 0]	[0.02, 0.27]	[0.02, 0.26]
1	1	0	1	1	0	0.11	0.03	0.02	[0, 0.26]	[0, 0.09]	[0, 0.09]
1	1	0	1	1	1	0	0.07	0.07	[0, 0]	[0.01, 0.16]	[0.02, 0.16]
1	1	1	1	0	1	0	0.03	0.05	[0, 0]	[0.01, 0.10]	[0.01, 0.10]
1	1	1	1	1	0	0	0.07	0.07	[0, 0]	[0, 0.17]	[0, 0.16]
1	1	1	1	1	1	0.56	0.34	0.22	[0.35, 0.76]	[0.10, 0.51]	[0.07, 0.48]

Figure 4 displays the estimated probability distribution for contact networks in households with two 0–5 year olds and two 19+ year olds. This figure graphically displays the penalized likelihood estimates in Table 3. Networks with estimated probabilities less than 0.03 are omitted from the plot. The complete network has an estimated probability of 0.65. The next most likely network has all contacts except contact between the two adults, and has an estimated probability of 0.12. The third most likely network includes all contacts except between the elder child and the female adult, and has an estimated probability of 0.08. The fourth most likely network has the elder child as an isolate, with all possible contacts occurring between the other three members. Prior to analyzing this data, we would not have expected this network to have a non-negligible probability in households with such young children, as they require parental care. However, it fits with two observations in our data set in which the elder 0–5 year old child was the respondent and reported no ties to other family members. We hypothesize that the child was not at home on the survey date. Since respondents were identified in advance of the survey date and mailed paper diaries to carry with them on the specified day, they were not necessarily at home. This isolate effect is one source of dependency in our network estimates. The plots show that in the five most likely networks, representing 97% of the probability mass, the elder child contacts two or three of the other three members, or contacts none of them. Networks in which the elder child contacts a single member are very unlikely. If the elder child contacts at least one other household member, then he or she is more likely to contact the other two.

Fig. 4.

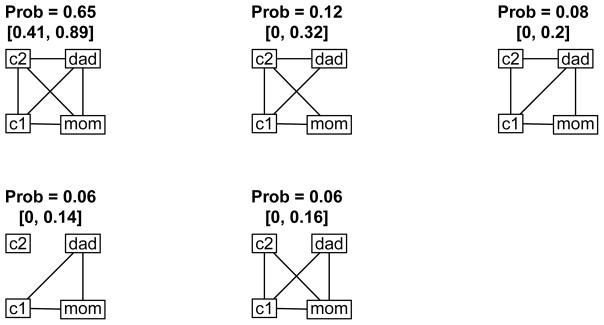
Estimated probability distribution for households with two 0–5 year olds and two 19+ year olds. Labels are: ch1 = younger child, ch2 = older child, ad1 = female adult, ad2 = male adult

We include plots analogous to Figure 4 for the other household types in the supplementary material. These plots show variation in contact patterns by household age composition. For example, households with two teenagers and two adults have a smaller estimated probability of the complete network (0.34), and networks in which one child does not contact one parent are more likely in this household type.

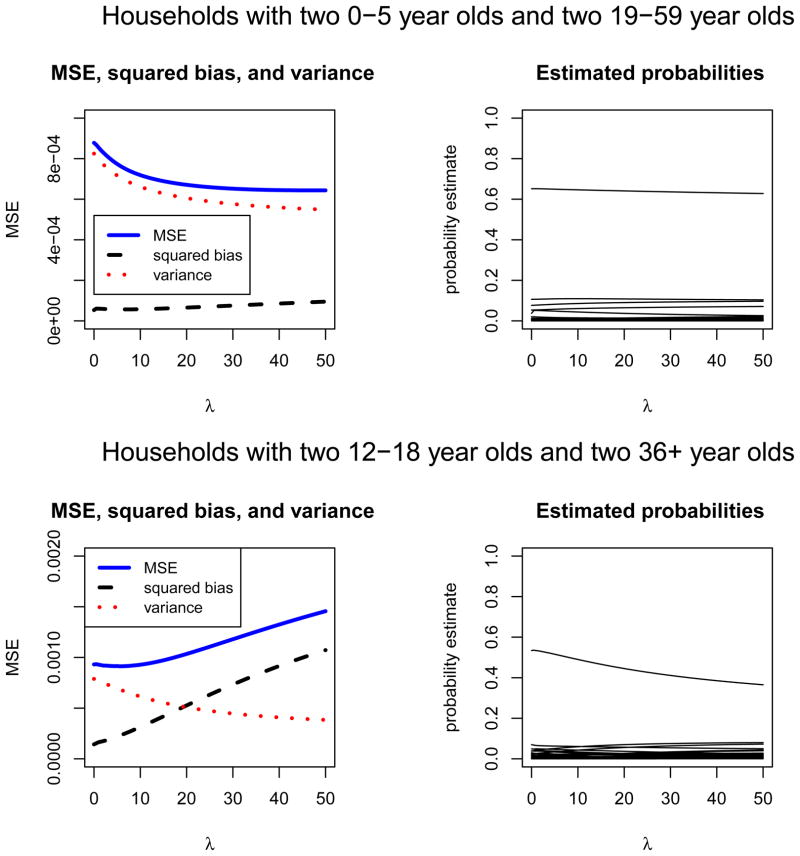
4.2. Simulation study results

Figure 5 shows the mean average squared error and its bias-variance decomposition from simulations based on the characteristics of two different household age compositions. In the younger household composition, after an initial decrease the mean averaged squared error stabilizes with increasing λ, due to decreasing bias and increasing variance. The initial decrease in mean average squared error shows the improvement in predictive performance as the weight on the penalty term is increased. The eventual stabilization of MSE shows similar predictive performance for a range of λ-values. Households with two 12–18 and two 36+ year olds show a different pattern from the simulations. For this household composition, MSE shows a very small decrease and then increases. The squared bias increases steadily while variance decreases monotonically. The right-hand plots show that as λ increases, the probability parameter estimates converge to the independence model estimates as we would expect.

Fig. 5.

Simulation results based on the characteristics of households with two 0–5 year olds and two 19+ year-olds. The left-hand plots show the mean squared error, squared bias, and variance averaged over probability parameters. The right-hand plots show the probability parameter estimates averaged over simulations.

5. Discussion

We have used egocentric data to estimate within-household contact networks, a key component of epidemic spread. We analyzed several different household types and found substantial differences in contact behavior between households of different age compositions. Contact density decreased as members’ age increased, suggesting that the higher transmission probabilities estimated for children than adults may be due to differences in contact behavior rather than biological differences. We also found evidence for departure from the “random mixing” assumption commonly used in epidemic models. A likelihood ratio test shows showed departure from the independence assumption required for random mixing in households with two small children, giving evidence for dependence in some household networks. The same test found no evidence for departure from independence in households with two teenagers and two adults, indicating that the independence model adequately represents contacts in these households. We conclude the independence assumption is appropriate for some household types but not others. One possible source of contact dependency is an isolate effect, in which members who are not at home make no contacts to at-home household members. One strength of our method is that it uses very few parametric assumptions. As such, our results can be used to build a parametric model based on the patterns we found or to assess assumptions made by existing models. This work also contributes to the field of social network inference. Using egocentric data collected from multiple small networks, we develop methodology to infer the probability distribution of the complete network with minimal assumptions. Our method could be applied to network data with the same structure from other settings.

Our method does require some assumptions. Our choice of smoothing penalty imposes a preference for probability distributions that are similar to an independence model. This is a lighter constraint than assuming independence, and permits dependence in our final estimates. We found this penalty to work better than the other two we tried. The adjacency penalty oversmoothed and produced unrealistic estimates, and the exchangeability penalty did not sufficiently constrain the parameter space.

An alternate solution to the identifiability problem would be a Bayesian approach, in which we restrict the parameter space by expressing our beliefs about the parameter values through prior distributions. However, the state of prior knowledge in the field is weak. The only paper we know of inferring household contact networks is Potter et al. (2011), and that paper uses the same data set we analyze here, so does not truly give prior knowledge. Therefore, we prefer the penalized likelihood approach scientifically. However, we did perform Bayesian analysis as an exploration. A Dirichlet distribution is an appropriate prior since its range satisfies the constraints on our parameter vector. A noninformative prior is a symmetric Dirichlet distribution with α = 1, giving equal weight to all possible parameter vectors. The posterior distribution was only slightly shifted from the prior distribution: it distributed probability mass fairly evenly among networks, with slightly higher mass (0.09) on the complete network. These results are unrealistic and inconsistent with the data. Since the data contain insufficient information to estimate our parameter, the prior has a strong influence on the posterior. We also tried symmetric Dirichlet distributions with α ranging from 0.01 to 2.0, but again the influence of the prior was so strong that patterns present in the data were not apparent in the posterior. Our understanding of social behavior might motivate us to create a prior distribution imposing a preference for denser networks, since we expect most household members to contact each other on a given day. However, Figure 2 shows that this prior distribution would be inappropriate for some household types. We are estimating 63 dependent parameters, and a prior distribution placing large weight on denser networks necessarily places negligible weight on networks with zero, one, or two contacts. Furthermore, the variance of the prior distribution for each parameter needs to be small, because priors with large variance were insufficient to constrain the parameter space. Thus, networks which are actually fairly likely given this data set received negligible probability mass in the posterior. We feel a Bayesian approach would be appropriate if we had a high level of confidence in our prior beliefs, and the exploration described here shows that the belief in denser household networks was not borne out by the data.

As Kim and Sanderson (2008) show, the relation between penalized likelihood and Bayesian methods is revealed by expressing a general penalized likelihood with penalty g(p) as:

$$PL(p\mid y)=\mathit{logL}(p\mid y)-\lambda g(p)=\mathit{log}(L(p\mid y)e^{-\lambda g(p)}),$$

Which is equivalent to a Bayesian approach where e^−λg(p) is a partially improper prior. This approach does not work in our case, because our independence penalty is itself a function of the data, and a Bayesian prior must not depend on the data. We believe this is why our method succeeds while Bayesian methods failed. The prior distributions in the Bayesian approach constrained our parameter space so heavily that results were unreasonably different from the data. Our penalty constrains our space in a way that is informed by and compatible with the data.

Our work has a number of limitations. First, we made assumptions regarding which contacted individuals are household members since this information was not collected, and we made assumptions about the identity of each contacted person based on their reported age and sex. In future surveys, we recommend having respondents identify which of their contacts are to household members. In addition, since we found evidence that some household members are away from home on the survey date, we recommend collection of home/away status for each household member.

Our approach is for networks of a fixed size and age composition and requires adequate sample size. Our data set contains 750 respondents, but because we performed analyses separately for each age composition, sample sizes ranged from 23–40. In two of the six household types we analyzed, the optimal tuning parameter was large and estimates were close to those assuming independence. The high contribution of the penalty to the estimates indicates a high level of non-identifiability for these household types. Our method works only for small networks because the proportion of the network observed from one respondent per household is $\frac{n-1}{\left(\begin{array}{c}n\\ 2\end{array}\right)}=\frac{2}{n}$, which decreases quickly with network size. In future surveys we recommend collecting contact reports from all household members to obtain the fullest possible understanding of the contact network. Our nonparametric approach will directly apply to completely observed household networks, and without missing data, the penalty term will be unnecessary and inference will be straightforward. In cases where nonresponse results in a small amount of missing data, the parameters may be identifiable with the nonparametric method. If not, our penalized likelihood approach can be easily modified to accomodate reports from multiple respondents per household.

The quality of the bootstrap approximation relies on the degree to which the empirical distribution approximates the true distribution. The sparseness of our data set, combined with the large number of parameters we are estimating, limit our ability to estimate uncertainty. We do not expect any confidence intervals for the MLE to perform well since the parameter is not identifiable. The nonparametric bootstrap may underestimate uncertainty in the independence model because for some dyads, 100% of contacts were observed, so each resample yields a probability estimate for that dyad of 1. As the penalized likelihood model is a combination of these two, uncertainty in its estimates may be underestimated as well. Furthermore, the confidence intervals for the penalized likelihood model do not take into account uncertainty arising from selection of the tuning parameter.

In our analysis, we assumed that contact behavior is the same on weekdays and weekends, and during the Easter holiday versus a non-holiday period. In fact, contact patterns may change during these periods, but sample sizes were too small to perform separate estimates since we performed estimates separately for each household age composition. A parametric model based on explicit assumptions of contact behavior could use the entire data set to estimate patterns, thus increasing our power to detect weekend and holiday effects.

One example of a parametric model was implemented in Potter et al. (2011). In that paper, the authors estimated a latent variable indicating whether each household member is at home on a given day. They assumed the home/away statuses of the different members were independent, and that contacts occurred independently between members at home, with contact probabilities depending only on age. They assumed that members away from home were not contacted. One advantage of this approach is that they combined reports from households of different sizes and age compositions, so increasing the sample size, while estimating a smaller number (20) of parameters. By estimating fewer parameters with a larger sample size, they were also able to estimate separate network effects for weekday vs. weekend and holiday vs. non-holiday. They found no evidence for differences in contact patterns between the weekday and the weekend. They found that holiday and non-holiday parameter estimates were statistically different, but did not show a clear and substantively important pattern in the differences. The disadvantage to the parametric model is the large number of assumptions required. In this paper, our goal was to perform estimation with as few assumptions as possible. The approach outlined here is well suited to that purpose, and is preferable when we have limited prior knowledge about our parameters of interest and a large amount of data. We recommend the parametric approach when researchers feel confident that model assumptions hold.

We have developed a new technique to infer small contact networks from egocentric data using minimal assumptions and applied it to estimate household contact networks in Belgium. Our estimates show departure from the random mixing assumption found in many epidemic models. We recommend collecting additional contact data and further investigation of the contact network structure and its relevance for infectious disease transmission.