Automated Analysis of Fundamental Features of Brain Structures

Abstract

Automated image analysis of the brain should include measures of fundamental structural features such as size and shape. We used principal axes (P-A) measurements to measure overall size and shape of brain structures segmented from MR brain images. The rationale was that quantitative volumetric studies of brain structures would benefit from shape standardization as had been shown for whole brain studies. P-A analysis software was extended to include controls for variability in position and orientation to support individual structure spatial normalization (ISSN). The rationale was that ISSN would provide a bias-free means to remove elementary sources of a structure’s spatial variability in preparation for more detailed analyses. We studied nine brain structures (whole brain, cerebral hemispheres, cerebellum, brainstem, caudate, putamen, hippocampus, inferior frontal gyrus, and precuneus) from the 40-brain LPBA40 atlas. This paper provides the first report of anatomical positions and principal axes orientations within a standard reference frame, in addition to “shape/size related” principal axes measures, for the nine brain structures from the LPBA40 atlas. Analysis showed that overall size (mean volume) for internal brain structures was preserved using shape standardization while variance was reduced by more than 50%. Shape standardization provides increased statistical power for between-group volumetric studies of brain structures compared to volumetric studies that control only for whole brain size. To test ISSN’s ability to control for spatial variability of brain structures we evaluated the overlap of 40 regions of interest (ROIs) in a standard reference frame for the nine different brain structures before and after processing. Standardizations of orientation or shape were ineffective when not combined with position standardization. The greatest reduction in spatial variability was seen for combined standardizations of position, orientation and shape. These results show that ISSNs automated processing can be a valuable asset for measuring and controlling variability of fundamental features of brain structures.

Introduction

Relative position and/or orientation of internal brain structures can vary for many reasons including differential growth of nearby structures (Lange et al. 1997), proximity to diseased or atypical brain tissue (Sparks et al. 2002), experience-dependent morphological change (Kochunov et al. 2003; Maguire et al. 2000) and genetic factors (Thompson et al. 2001). It is therefore desirable to have a reliable automated means to measure these relationships. Spatial incidence maps (Mazziotta et al. 1995, 2002) were devised to characterize spatial variability of brain structures within a standard reference frame, but variability encoded in these maps is a mixture of spatial (position, orientation) and structural (size, shape) components. We present an alternative approach to characterize a brain structure’s spatial and structural features by direct measurement. We recently showed that whole brain spatial normalization could be achieved while preserving mean volumes of brain structures (Lancaster et al. 2010), and have now extended this processing to individual structures. Individual structure spatial normalization (ISSN) software provides automated measures of a brain structure’s position, orientation, size, and shape and methods to control for variability in each.

To standardize spatial measures brains should first be registered to an x-y-z coordinate reference frame using rigid-body transforms. Several software packages (e.g. SPM, FSL, AFNI, and Mango) provide rigid-body options to register 3-D brain images to standard template brains. Within the reference frame the anterior commissure is the origin, the AC-PC line the y-axis, the mid-sagittal plane the y-z plane, and the x-axis is through the origin and perpendicular to the mid-sagittal plane (Lancaster and Fox 2009). Variability in delineating individual brain structures can confound spatial and structural measures, but strict delineation rules and/or automated segmentation methods (Powell et al. 2008) help alleviate this problem. ISSN’s basic functional features were verified using a set of ellipsoids of known dimensions and orientations. ISSN was then used to evaluate nine brain structures from the LPBA40 atlas to measure spatial and structural features and to control for variability in position, orientation, and shape within the standard reference frame.

Materials and Methods

ISSN Software

Brain structure measurements by ISSN are based on principal axes analysis, a method that has been used for brain image registration (Alpert et al. 1990; Toga and Banerjee 1993; Schormann and Zilles 1997), shape comparisons in central sulcus (Le Goualher et al. 2000), to support brain structure classification (Mangin et al. 2004), and for whole brain spatial normalization (Lancaster et al. 2010). ISSN is a multi-platform Java application freely distributed from the Mango download site (http://ric.uthscsa.edu/mango/download.html). Principal axes analysis is performed on standard bit-mapped ROIs formulated using the Mango image-processing software system. The ISSN ROI file format is identical to that used by FSL. Analysis of uniform ROIs avoids inconsistencies that can arise from tissue variability within a structure. ROI volume is the voxel sum multiplied by the voxel volume (mm³/voxel). ROI position is the average voxel location. Groups of ROIs for a brain structure are batch processed with options to control for variability in position, orientation, and P-A sizes individually or in combinations. P-A size control is achieved by scaling along the three principal axes directions. ISSN software output options include spatial incidence maps, transformed ROIs and images, and average brain images. Subject-by-subject measurements and group statistics are saved to a multi-tab Excel spreadsheet.

ISSN Standardization Methods

ISSN’s spatial normalization is based on group-derived standards for position, orientation, and shape. The average position of a structure’s ROI is its “position standard”.

We used the triplet of P-A size measures from the three principal axis eigenvalues to formulate shape standards. These eigenvalues are spatial variances measured from the center along principal axis directions. The square roots of eigenvalues are spatial standard deviations, which indicate size of the associated axes, so we designated these “P-A sizes”. The product of the magnitude of the P-A sizes relates to overall size (volume), and their magnitudes relate to overall shape. The average P-A sizes were the “shape standards”.

A brain structure’s orientation is defined as the orientation of its principal axes, specified by the three unit eigenvectors. We determined a group-standard unit vector for each eigenvector grouping (see Fig. 1, Appendix A). Two problems were encountered: orientation outliers and varying directional sense. We developed a method to manage both (Appendix B), and this was done prior to determining group-standard unit vectors. While structure volumes were measured as part of ISSN’s ROI analysis, volume was our dependent variable and was therefore not directly manipulated.

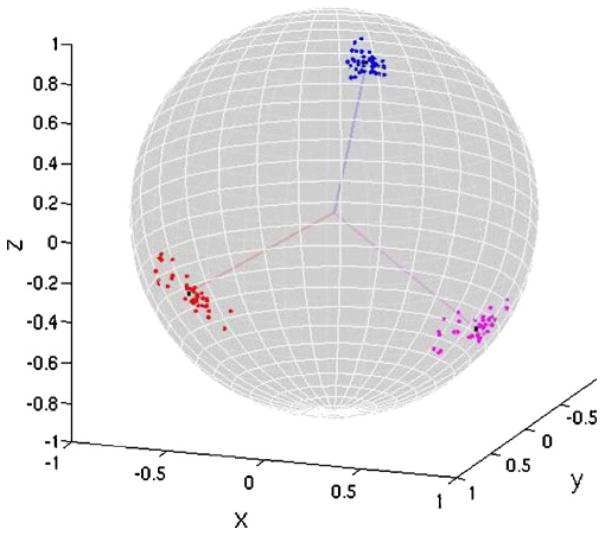
Fig. 1.

Tips of eigenvectors from right hippocampus of LPBA40 subjects mapped onto the surface of a unit sphere. Lines from center of sphere are the group standard orientation unit vectors

A transform matrix was formulated to translate each brain structure to the group standard position, rotate principal axes to match group standard orientations, and scale along principal axes to match the group standard shape. Individually, these normalizations are referred to as position, orientation, or shape standardization.

Test of ISSN Software

Principal axes orientations and sizes track exactly with ellipsoid’s semi-axes, so ellipsoids were chosen for operational testing of ISSNs principal axes software. Ellipsoids were modeled with sizes and orientations proportioned to a typical internal structure (left caudate) from the LPBA40 atlas. Ellipsoid diameters ranged from 34 to 146 mm with orientations up to 25° from image axes. Volumes measured by ISSN were within 0.2% of those calculated analytically. Following combined position-shape standardization the group mean volume was minimally altered (less than 1.5%), but the coefficient of variation of volumes dropped from 28.0% to 0.2%. Post processed P-A sizes differed by less than 0.2%, and P-A angular variability dropped from ~8° to less than 0.1°, verifying shape and orientation standardization. These test results confirmed that ISSN software’s principal axes analysis and standardization routines worked as designed.

Tested Brain Structures

The Probabilistic Brain Atlas (LPBA40) distributed by UCLA’s Laboratory of Neuro Imaging (LONI) was used to evaluate ISSN using nine of its brain structures (Shattuck et al. 2008). This atlas contains brains from 40 healthy adult volunteers (ages 16–40, 20 males). During atlas development rigid-body registration of brains to the MNI-305 reference frame (Evans et al. 1993) was done using ten user-defined landmarks (Narr et al. 2002) and least squares fitting with the Register software (MacDonald et al. 1994). Since brain size and shape were not altered, this set of brain images and structures were ideal to evaluate ISSNs ability to control for individual structure variability within a standard reference frame. 3-D bit-mapped regions of interest (ROIs) were made from images of the “delineation” subset (1-mm isotropic spacing) using Mango’s 3-D shrink-wrap procedure (ric.uthscsa.edu/mango). ROIs were made for whole brain, cerebral hemispheres, cerebellum, brainstem, three deep brain structures (hippocampus, caudate, and putamen), and two gyral structures (inferior frontal gyrus and precuneus). Volumes of the Mango formulated ROIs matched those reported by Shattuck et al. 2008.

Spatial and Structural Measures

We used ISSN to measure position, volume, P-A eigenvalues, and P-A eigenvectors by components for all 40 brains in the nine brain structures. These data were saved in a multi-tab spreadsheet file, which was analyzed using Microsoft Excel.

Shape and Volume

A previous study showed that variability in whole brain volume was greatly reduced by shape standardization (Lancaster et al. 2010), while preserving the mean volume, but it was not clear how shape standardization would impact volumetric variability in other brain structures with varying shapes. In this study we used shape standardization to determine the impact on mean volume and volumetric variance of nine brain structures. The shape standardization was done by determining the three scaling factors in each brain to adjust P-A sizes to match the group standard and then scale volume using their product. This analysis did not require spatial normalization but rather was done using measurements made by the ISSN software which were stored in an Excel style spreadsheet.

Variability in a Standard Reference Frame

ISSN provides support for creating spatial incidence maps, which represent spatial variability for a group of brain structures in a standard reference frame (Mazziotta et al. 1995, 2002). The extent of 3-D incidence maps (volume of the union of all ROIs) was used to gauge residual spatial variability following standardization of position, orientation and shape (and combinations) for the nine brain structures from LPBA40 atlas. Spatial incidence maps were formulated using a two-step process:

1. ROIs were transformed using 9-parameter 4×4 affine matrices formulated for standardization. Interpolation of transformed ROIs was done using the method of Collins et al. 1994.

2. Mask images (inside ROI=1, outside ROI=0) of the transformed structures were summed and averaged to form incidence maps with incidence ranging from 0 to 100%.

The objective was to determine the effect of ISSN’s standardizations on overall spatial variability in a standard reference frame for each brain structure, with the level of control indicated by the reduction in extent of incidence maps. Each 40-brain incidence map had a numeric precision of 2.5%. The 3-D surfaces formulated to fit the extent of incidence maps show how extent is significantly reduced by standardization in the caudate (Fig. 2).

Fig. 2.

Surface renderings of extent for caudate incidence maps without standardization (wireframe) and following combined standardizations (grey)

Internal Structure Detail

Though spatial incidence maps depict registration of exterior boundaries for a group of brain structures they provide little information concerning registration within a structure. To investigate registration of internal detail we tested ISSN applied to whole brain hemispheres where anatomical detail is more readily identified. The quality of registration of whole brain hemispheres images is reflected in the level of anatomical detail preserved in average images. We used ISSNs position and size standardization and compared anatomical detail before and after standardization for average images of the LPBA40 brains.

Results and Analyses

Spatial and Structural Measures

The fundamental features measured by ISSN for nine brain structures in 40 normal individuals are presented in Table 1. Mean x-coordinates for whole brain, hemispheres, cerebellum, and brainstem were similar ranging from 0.12 to 0.62 mm from the origin (anterior commissure). Whole brain and hemispheres positions were posterior (~16–21 mm) and superior (~13–18 mm) to the anterior commissure. Mean y- and z-coordinates tracked as expected for a structure’s general location, as seen for cerebellum, with its large negative y & z coordinates. The average x-coordinate of combined left and right brain structures was within 0.5 mm of the whole brain value, indicating general left-right symmetry. Left side structures were slightly more posterior and inferior. Variance in position was least for the x-coordinate and tended to be largest in the direction of the largest principal axis for most structures. The location of the AC in the LPBA40 brain atlas based on visual inspection of the 40 brain images was x=90.4, y=88.7 and z=114.5 mm.

Table 1.

Summary of spatial and structural measures made by ISSN from the LPBA40 atlas brains. Left brain measures have grey background. Data are mean and (standard deviations)

Structure	Positiona (mm)			Axis orientationb						P-A size (mm)			Volume (mm3)
	x	y	z	x2	y2	z2	x1	y1	z1	s3	s2	s1
whole brain (N=40)	0.54 (0.81)	−20.58 (1.99)	12.57 (1.47)	0.995 (0.007)	0.020 (0.058)	−0.010 (0.078)	−0.019 (0.061)	0.993 (0.008)	0.095 (0.044)	26.4 (1.14)	30.3 (1.38)	38.4 (1.63)	1,337,343 (127,488)
Hemispheres (N=40)	0.62 (0.86)	−16.13 (2.21)	17.75 (1.52)	0.996 (0.012)	0.021 (0.087)	−0.007 (0.030)	−0.022 (0.088)	0.987 (0.012)	−0.128 (0.036)	23.2 (1.04)	31.2 (1.43)	38.3 (1.68)	1,179,970 (112,542)
Cerebellum (N=38)	0.12 (0.85)	−60.23 (3.60)	−26.58 (2.74)	−0.007 (0.03)	0.935 (0.051)	−0.221 (0.275)	−0.999 (0.001)	−0.005 (0.029)	0.008 (0.022)	10.8 (0.57)	12.6 (0.84)	24.4 (1.30)	134,140 (17,646)
Brainstem (N=40)	0.35 (0.69)	−29.08 (1.56)	−23.77 (1.52)	0.997 (0.004)	−0.022 (0.071)	0.012 (0.035)	−0.004 (0.023)	0.428 (0.051)	0.902 (0.024)	6.38 (0.32)	7.59 (0.58)	16.3 (0.61)	29,590 (3365)
L IFG (N=30)	−41.12 (1.82)	26.92 (3.78)	9.98 (1.99)	0.130 (0.244)	−0.371 (0.110)	−0.877 (0.080)	0.173 (0.081)	−0.889 (0.054)	0.398 (0.112)	5.91 (0.41)	7.14 (0.70)	14.80 (1.22)	23,071 (4977)
R IFG (N=34)	41.74 (2.33)	27.34 (3.39)	10.84 (2.38)	−0.104 (0.241)	−0.414 (0.119)	−0.862 (0.074)	−0.149 (0.105)	−0.873 (0.057)	0.436 (0.109)	6.12 (0.44)	7.51 (0.66)	14.51 (1.19)	24,795 (5153)
L precuneus (N=37)	−4.72 (1.79)	−54.70 (3.41)	41.67 (3.13)	−0.130 (0.086)	−0.862 (0.108)	0.397 (0.255)	0.045 (0.041)	0.395 (0.254)	0.875 (0.110)	3.18 (0.30)	8.60 (1.01)	11.94 (1.13)	10,725 (2277)
R precuneus (N=38)	5.66 (2.11)	−54.11 (3.08)	42.16 (2.93)	0.051 (0.070)	−0.873 (0.152)	0.319 (0.330)	−0.024 (0.027)	0.381 (0.330)	0.877 (0.153)	3.15 (0.36)	8.35 (0.88)	11.71 (1.14)	10,497 (1908)
L putamen (N=40)	−23.38 (1.16)	−0.46 (2.52)	5.30 (1.24)	0.122 (0.061)	−0.174 (0.081)	−0.972 (0.015)	0.272 (0.041)	−0.937 (0.021)	0.202 (0.074)	2.75 (0.21)	4.94 (0.27)	9.77 (0.66)	4,249 (531)
R putamen (N=40)	24.48 (1.62)	0.60 (2.12)	5.15 (1.34)	−0.083 (0.102)	−0.171 (0.080)	−0.973 (0.018)	−0.301 (0.045)	−0.931 (0.019)	−0.189 (0.066)	2.80 (0.19)	4.83 (0.29)	9.89 (0.64)	4,206 (504)
L Hcp (N=40)	−21.98 (1.44)	−14.67 (1.91)	−11.49 (1.50)	−0.886 (0.053)	−0.303 (0.103)	0.314 (0.106)	0.412 (0.104)	−0.825 (0.047)	0.365 (0.055)	2.76 (0.19)	4.79 (0.34)	8.78 (0.81)	3,907 (528)
R Hcp (N=40)	22.76 (1.26)	−13.76 (1.64)	−11.46 (1.52)	−0.851 (0.056)	0.366 (0.102)	−0.340 (0.118)	−0.484 (0.091)	−0.789 (0.058)	0.360 (0.048)	2.82 (0.20)	4.89 (0.33)	8.72 (0.62)	4,120 (527)
L caudate (N=40)	−10.80 (1.33)	6.19 (2.73)	13.57 (1.82)	−0.534 (0.100)	−0.520 (0.059)	−0.654 (0.057)	0.123 (0.037)	−0.821 (0.042)	0.552 (0.062)	2.22 (0.28)	4.05 (0.43)	10.47 (0.95)	2,972 (558)
R caudate (N=40)	11.34 (1.39)	6.59 (2.32)	14.29 (1.68)	0.544 (0.113)	−0.507 (0.065)	−0.653 (0.063)	−0.137 (0.049)	−0.831 (0.037)	0.532 (0.054)	2.15 (0.29)	4.00 (0.42)	10.40 (0.82)	2,856 (623)

^aPosition is x-y-z coordinate relative to the anterior commissure as the origin in each subject.

^bOrientation is given as the x-y-z components of the two largest eigenvectors, with eigenvector one as the largest.

Mean orientations of the two largest principal axes eigenvectors with closest x-, y-, or z-axis are indicated in Table 1. The largest principal axis of most brain structures was directed nearest to the y-axis. However, cerebellum’s largest principal axis was x-directed while brainstem and precuneus were more z-directed. Little differences were seen in mean orientation of left vs. right side structures in other eigenvector components. Inspection of P-A sizes indicated a size-related change in shape with smaller volume structures tending to be more elongated.

Shape and Volume

Following ISSNs shape standardization the mean values for position, orientation, and total volume—reported in Table 1—did not change. However, volumetric standard deviations for most brain structures dropped substantially compared with standard deviations for whole brain spatial normalization (Table 2).

Table 2.

Volumetric variability following shape standardization

Structure	Standard deviation (mm3)		Variance
	aGSNa	ISSN	Explained	Unexplained
Whole brain (N=40)	11,947	11,947	0	100%
Hemispheres (N=40)	16,216	9,996	62%	38%
Cerebellum (N=38)	11,803	2,751	95%	5%
Brainstem (N=40)	2,261	1,075	77%	23%
L IFG (N=30)	4,344	1,590	87%	13%
R IFG (N=34)	5,318	1,668	90%	10%
L precuneus (N=37)	1,668	826	75%	25%
R precuneus (N=38)	1,498	679	76%	24%
L putamen (N=40)	489	320	57%	43%
R putamen (N=40)	447	320	56%	44%
L Hcp (N=40)	347	200	67%	33%
R Hcp (N=40)	426	205	76%	24%
L caudate (N=40)	447	333	51%	49%
R caudate (N=40)	554	265	77%	23%

^aStandard deviation for whole brain shape normalization called aGSN (Lancaster et al. 2010).

Variability in a Standard Reference Frame

ISSN standardizations with the greatest reduction are highlighted in overall spatial variability (extent of incidence maps) are highlighted in Table 3.

Table 3.

Extent of incidence map volumes (mm³) for nine brain structures. Data are without processing and for individual and combined standardizations in position (p), orientation (o), and shape (s) by ISSN

Structure	Without	Individual			Combined
	-	p	o	s	po	ps	os	pos
Whole brain	1874960	1820665	1921923	1690975	1872527	1634843	1719754	1671857
Hemispheres	1675497	1621993	1704247	1508316	1646461	1453405	1524355	1459726
Cerebellum	246363	209940	259144	235688	224094	191767	247776	207651
Brainstem	59063	51279	57876	57391	49417	48194	56059	46220
R IFG	76237	60960	74311	71167	59629	53721	69128	52928
L Precuneus	40819	30309	41690	38033	30794	28564	38473	28154
R Putamen	14415	9293	14121	14322	8929	9159	13929	8570
R Hcp	13848	9650	13959	13624	9156	9137	13227	8796
L Caudate	10845	7767	10995	11040	7082	7227	10796	6408

Grey values represent the smallest incidence map extent for individual or combined controls.

Position Standardization (p)

Position standardization produced the largest reduction in extent for most brain structures (Table 3). Residual spatial variability of whole brain and hemispheres was only slightly reduced by position standardization, since position had been controlled during atlas development. Position standardization was more effective for smaller internal brain structures, where the reduction in extent approached 30% for putamen, hippocampus and caudate (see Fig. 2 for caudate).

Shape Standardization (s)

Shape standardization produced the largest reduction in extent for whole brain and cerebral hemispheres (Table 3). This was expected since brain size was not controlled when preparing the LPB40 brain atlas. Shape standardization produced little or no reduction in extent for brainstem, cerebellum, putamen, hippocampus, or caudate (0–5%). For IFG and precuneus the reduction in extent was intermediate at ~7%.

Orientation Standardization (o)

Orientation standardization had little effect on extent for any structure. However, orientation control alone led to slightly larger extents for whole brain, hemispheres, cerebellum and several smaller structures. The lack of reduction in spatial variability in cerebellum was assumed to be due to its varying shape (see Discussion).

Combined Standardizations

The largest reduction in extent for whole brain, hemispheres, and cerebellum was seen for combined position and shape standardization (ps in Table 3). For all other brain structures, combined position, shape, and orientation standardization (pos in Table 3) resulted in the smallest extent. Position standardization was necessary before orientation and shape standardizations could be effective. The complimentary effect is seen where combined standardizations provided good control of spatial variability for all structures.

Internal Structure Detail

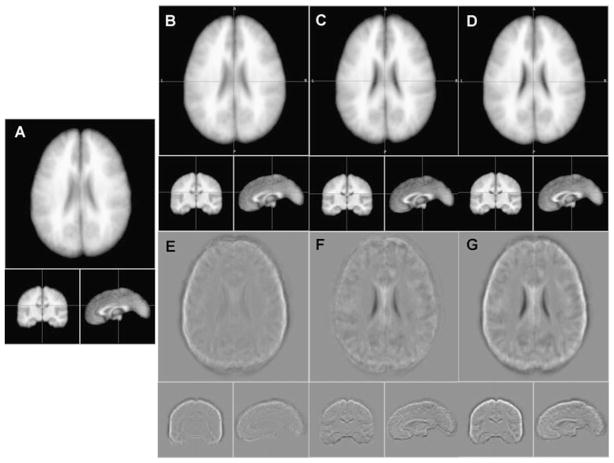
Shape standardization provided more improvement in superficial anatomical detail than that deeper within the brain (Fig. 3B & E). Position standardization showed more improvement in anatomical detail deeper than superficially (Fig. 3C & F). Improvement in both deep and superficial anatomical detail was seen with combined position and shape standardization (Fig. 3D & G), and overall internal anatomical detail was judged best for this combination. Improvement in the corpus callosum boundary in the mid-sagittal sections and temporal lobe contrast in coronal sections support this (Fig. 3A to D). These results are consistent with the study of extent of whole-brain incidence maps, where the smallest extent for whole brain was for combined position and shape standardization (p-s in Table 3). Orientation standardization was not included in this study, but visual inspection indicated that it did not improve detail beyond that provided by position-shape standardization. While this test was only for whole brain hemispheres, it suggests that position and shape standardization can help register internal anatomical details for other brain structures.

Fig. 3.

The 40-subject average image (a), and averages after shape standardization (b), position standardization (c), and combined (d). (e) is image (b-a), (f) is image (c-a) and (g) is image (d-a) to highlight areas with differences in anatomical detail

Discussion

Comparing Features

As indicated in the introduction fundamental features of internal brain structures can vary for many reasons including differential growth of nearby structures (Lange et al. 1997), proximity to diseased or atypical brain tissue (Sparks et al. 2002), experience-dependent morphological change (Kochunov et al. 2003; Maguire et al. 2000) and genetic factors (Thompson et al. 2001). ISSN’s measures of brain structures from individuals or group studies can be used to test for differences in position, orientation, shape, and volume compared with values for the LPBA40 atlas reported in Table 1. For position or orientation testing brain images must be registered to the standard reference frame used for the LPBA40 atlas controlling for position and orientation. Orientation of a structure can be computed relative to 1) whole brain orientation, 2) a structure’s group standard orientation, or 3) other structures’ orientations. Standard deviations in orientation of structures about their group standard orientation (Fig. 1) are provided in Table 4 to support formal statistical testing.

Table 4.

Variability in principal axes orientation reported as angular standard deviations from group standard orientations. (Left brain structures greyed)

Structure	SD3 (axis)	SD2 (axis)	SD1 (axis)
whole brain-	2.56° (z)	3.14° (x)	2.85° (y)
Hemispheres-	1.17° (z)	3.89° (x)	3.92° (y)
Cerebellum-	10.47° (z)	10.34° (y)	1.00° (x)
Brainstem-	2.63° (y)	2.44° (x)	1.80° (z)
L IFG-	8.62° (x)	8.60 (z)	3.89° (y)
R IFG-	8.06° (x)	8.60° (z)	4.00° (y)
L precuneus-	2.92° (x)	7.63° (y)	8.00° (z)
R precuneus-	2.23° (x)	10.07° (y)	10.46° (z)
L putamen-	1.96° (x)	2.62° (z)	2.51° (y)
R putamen-	4.20° (x)	4.46° (z)	2.36° (y)
L hippocampus-	3.71° (z)	4.48° (x)	4.02° (y)
R hippocampus-	4.13° (z)	4.84° (x)	3.40° (y)
L caudate-	3.88° (x)	3.80° (x,y,z)	2.50° (y)
R caudate-	4.44° (x)	4.42° (x,y,z)	2.11° (y)

Subscripts indicate smallest (3) to largest (1) principal axes.

(x,y,z) indicates no clear axis association.

Shape and Volume

It is common practice to control for variability of whole-brain size in volumetric studies of brain structures. The shape standardization provided by ISSN is a useful tool that provides additional insight into the nature of volumetric variability. Shape standardization does not alter mean volumes; so resulting mean values are comparable with pre-standardized mean values, i.e. the naturally developed mean volumes. While mean volumes are unaltered by shape standardization, volumetric variance is greatly reduced for internal brain structures compared to whole brain size control alone (Table 2). Shape standardization removes the component of volumetric variance explained by overall shape variability, and the residual or unexplained volumetric variability is assumed due to variability in higher order structural features. To compare shape standardization with traditional volumetric studies we recommend that users calculate volumes using both methods, one controlling for brain size and the other shape standardizing. With this approach one can directly assess volumetric variance associated with overall shape variability.

Managing Orientation Outliers

Variability in orientation of several structures (cerebellum, IFG and precuneus) was higher than in other structures (Table 4). Visual inspection of ROIs for IFG and precuneus indicated that orientation variability was associated with their delineation, where an adjacent gyrus had been inadvertently included. To help deal with this we developed an orientation outlier detection scheme based on disparity of individual structure’s orientation from the group’s median vector orientation (Appendix B). Several rejection thresholds were evaluated and a threshold of 40 degrees was selected as most reasonable for rejection of outliers, while retaining structures for subjects with low orientation variability. This threshold is adjustable within the ISSN software.

Unlike IFG and precuneus, orientation outliers in cerebellum appear to result from natural variability in shape. In one outlier, orientation differences were so large that the second and third eigenvector’s directions switched between A-P and S-I directions, so axis association with eigenvector order was incorrect. There were no subjects where the two smaller axes magnitudes were nearly identical, further reason to distinguish the orientation outliers in cerebellum as different shapes rather than the result of continuous shape variability. Most brain structures were outlier free and had large reductions in volumetric variance following shape standardization (Table 2).

Reviewing Structure ROIs

ISSN software requires that structures be segmented from the brain and saved as ROIs. While progress is being made in improving and automating brain structure segmentation, we caution users to carefully review segmentations. As indicated above ISSN can be used to assist with this review based on its orientation outlier detection feature. Data from outliers are placed in a separate tab in the excel workbook by ISSN, so users can review these data and associated ROIs to check for problems and potentially correct before proceeding. If corrections are made running ISSN again can be used to test for success.

Dealing with Symmetrical Structures

For brain structures which approach symmetry about an axis, such as the eyeball, principal axes analysis might not be effective. More specifically, should there be symmetry about an axis, orientation about that axis is not defined. For P-A analysis symmetry is indicated by identical magnitudes of principal axes, but for all brain structures evaluated in this study the magnitude of principal axes were clearly different (Table 1, P-A sizes), so principal axes analysis and alignment were appropriate.

Spatial Variability in a Standard Reference Frame

Following registration of brains to a spatial reference frame residual spatial variability of brain structures is due to variability in position, orientation, shape/size, and other higher order effects. In this study standardization in position provided the largest reduction in this residual spatial variability, while orientation standardization produced the least. Combined standardization in position, shape, and orientation provided a large reduction in spatial variability for all structures. Incidence map extent for larger brains structures (whole brain, hemispheres, and cerebellum) approached a volume approximately 25% larger than their group-mean volumes for combined standardizations (Table 3 vs. Table 1). This result helps explain why average brain templates tend to be larger than the brains used to formulate them. Incidence map extents for internal brain structures with combined standardization approached a volume that was relative larger, approximately twice that of mean volumes of individual structures. The lesser reduction in spatial variability for these smaller brain structures is assumed to be associated with their increased surface area to volume ratio, where regional surface variability accounts for a larger portion of overall spatial variability. ISSN’s combined position, shape and orientation standardization removes spatial variance associated with overall position, shape/size, and orientation and should be a good preprocessing step to study subtle differences in a structure’s features.

Conclusions

ISSN’s principal axes analyses software provides unbiased measures of a structures fundamental features including position, volume, shape, and orientation. These features can be compared with measures tabulated for nine structures from the forty normal brains in the LPBA40 atlas for individual or group of brain studies (Table 1). Shape standardization provides a means to reduce volumetric variation associated with overall shape variability. The template-free approach provided by ISSN can standardize position, orientation, and shape/size as a preprocessing step for regional analysis of brain structures.

Appendix A

As illustrated in Fig. 1 tips of principal axes unit vectors originating from the center of a unit sphere cluster into three groups along the sphere’s surface. The angle (θ) between the tips of any pair of unit vectors (û&v̂) can be calculated as the arccosine of their dot product:

$$\theta ={cos}^{-1}(\widehat{u}·\widehat{v})$$ (A.1)

For a unit radius sphere this angle is also arclength expressed in radians, where arclength is the shortest distance between two vector tips along a great circle of the unit sphere. The objective was to find a unit vector (ŵ) such that the summed arclengths (distances) between it and other vectors (v̂_i) in a group would be a minimum, and assign it as the group standard unit vector. The arclengths between a vector within a group and ŵ range from 0 to approximately π/4 radians, while the corresponding dot products range from 1 to 0.707. There is a 1:1 inverse mapping between arclengths and dot products within these ranges such that “minimizing summed arclengths” can be accomplished by “maximizing summed dot products”. The problem is therefore reduced to finding a vector ŵ that maximizes the dot product sum “S”

$$S={\sum }_i\widehat{w}·{\widehat{v}}_i$$ (A.2)

The first step is to expand A.2 into a sum of component products

$$S={\sum }_i(x_w{x}_i+y_w{y}_i+z_w{z}_i)$$ (A.3)

The next step is to use the constraint that ŵ must be a unit vector such that

$$z_w=\pm \sqrt{1-(x_w^2+y_w^2)}$$ (A.4)

Substitution of z_w from A.4 into A.3 leads to an equation for S in terms of x_w and y_w:

$$S={\sum }_i\left(x_w{x}_i+y_w{y}_i\pm \sqrt{1-\left(x_w^2+y_w^2\right)}{z}_i\right)$$ (A.5)

Setting both $\frac{\partial S}{\partial x_w}$ and $\frac{\partial S}{\partial y_w}$ equal to zero leads to a pair of equations that can be solved for x_w and y_w that maximize S:

$$\begin{array}{l}{z}_w{\sum }_i{x}_i=\pm x_w{\sum }_i{z}_i\\ z_w{\sum }_i{y}_i=\pm y_w{\sum }_i{z}_i\end{array}$$ (A.6)

Additional algebraic manipulation involves squaring both sides of A.6 and using A.4 to remove z_w from the result and simplifying. The x, y, and z components for the standard unit vector simplify to

$$\begin{array}{l}{x}_w=\frac{\overline{x}}{{\overline{x}}^2+{\overline{y}}^2+{\overline{z}}^2}\\ y_w=\frac{\overline{y}}{\sqrt{{\overline{x}}^2+{\overline{y}}^2+{\overline{z}}^2}}\\ z_w=\frac{\overline{z}}{\sqrt{{\overline{x}}^2+{\overline{y}}^2+{\overline{z}}^2}}\end{array}$$ (A.7)

where x̄, ȳ, and z̄ are mean values for x, y, and z components of the group’s eigenvectors. The sense in A.7 is that of the mean values calculated from the group of sense corrected eigenvectors (Appendix B). Three standard unit vectors, one for each principal axis group, are calculated using A.7. These standard unit vectors should be orthogonal and this property was verified for all structures.

Appendix B

Two corrections are needed prior to assessing the group-standard orientation of a brain structure. The first correction is needed if a structure’s eigenvector orientation is inconsistent with the dominant orientation of the group, i.e. an outlier. The second correction handles cases where the directional sense of an eigenvector is opposite to the dominant directional sense of the group. During P-A analysis eigenvector directional sense can switch due to differences along a principal axis direction.

Preliminary testing of eigenvectors showed that the characteristic orientation of a brain structure could be robustly represented using group median vectors; so three median eigenvectors were determined, one for each principal axis. Use of median rather than mean eigenvectors avoids effects of outliers and problems with mean values due to mixed +/− directional sense. We formulated the median vector for a group of eigenvectors such that the median vector’s x, y and z components were the medians of the eigenvectors x, y and z components for the group. This median vector is called a Manhattan median (Krause 1986). Median vectors formulated in this manner are not guaranteed to be orthogonal or of unit length. Absolute orthogonality was not required since median vectors were only used for sense testing and control. We adjusted the median vectors to be unit length for subsequent processing.

Both outlier and sense tests were done by analysis of the dot product between individual eigenvectors and corresponding median eigenvectors. The magnitude of the dot product is a measure of how closely aligned one unit vector is to the other, ranging from 0 (orthogonal) to 1 (parallel). An eigenvector was considered an outlier if the dot product was less than a critical value (0.75 indicates ~40-degee orientation difference). The sign of the dot product determines relative directional sense, so a negative dot product indicates opposite sense. In that case the eigenvector’s sense is switched to match that of the median eigenvector. Switching sense changes signs of the x-, y- and z-components, which reflects the vector through the origin. The sense-switching algorithm preserves orthogonality and magnitude, while providing consistent orientation sense for all structures in all subjects. This preprocessing was needed to support averaging of eigenvectors to determine orientation standards (Appendix A).