Figure 1.

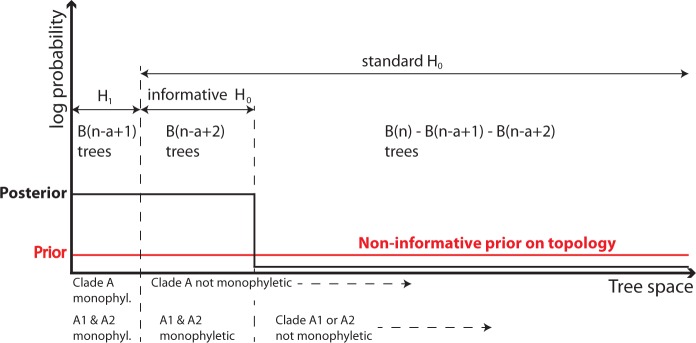
Schematic illustration of the Bayes factor test of the hypothesis that A is a monophyletic group (H₁) against the hypothesis that it is not (H₀). We assume that A consists of two strongly supported subclades, A1 and A2, but that the rest of the tree is unresolved such that there is no evidence that A1 and A2 together form a monophyletic group. The Bayes factor compares the average height of the posterior over the prior tree space of each hypothesis. When using a standard H₀, the signal is spread over a large tree space, and the test suggests that H₁ is strongly supported. If we use an informed prior for H₀ by restricting the tree space to those trees that have A1 and A2 monophyletic, then the Bayes factor correctly identifies that there is no support for or against H₁ over H₀, as the average height is the same. A posterior odds test compares the total probability mass under each hypothesis (the area under the posterior distribution), and is therefore not as strongly influenced by the size of the tree space as the Bayes factor.