Figure 1.

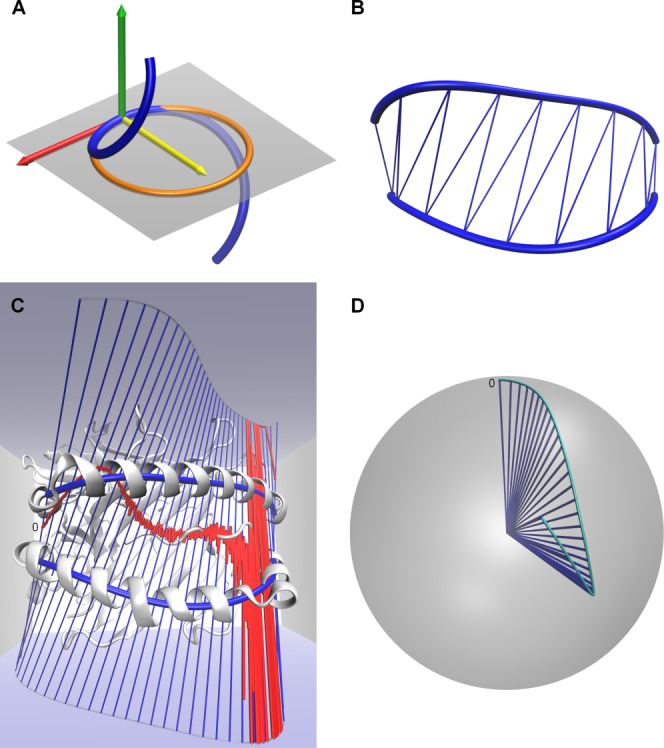
Differential geometric parameters for MH α-helices: (A) Representation of curvature and torsion: Curve (blue) with a local coordinate system in a curve point spanned by tangent vector (red), principal normal vector (yellow), and binormal vector (green). In the plane spanned by tangent vector and principal normal vector (gray), the circle of curvature (orange) is illustrated. For different views of this picture, we refer to Figure S1 of the Supporting Information. (B) Course-grained area: Two curves (blue) represent the two α-helices of the MH. We calculated the area by a triangulation of the ruled surface between the two curves. For different views in a representative X-ray structure, we refer to Figure S2 of the Supporting Information. (C) Ruled surface generated by the curves (blue lines) representing the two α-helices of the MH H-2Kb (white) with the PDB accession code 1s7q (compare Test set 2: MH1 cross evaluation). The coarse-grained rulings (blue) originate from a movement of a straight line along the two curves. The striction curve (red), representing the evolution of the distribution parameter, illustrates in a graphical way the skew parts (rulings are skew to each other) and the torsal parts (points of the striction curve converges to infinity). For different views of this picture, we refer to Figure S3 of the Supporting Information. (D) Director cone (course-grained blue rulings fixed in origin) with the spherical curve (cyan) on the unit sphere. The conical curvature measures the curvature on the unit sphere of the spherical curve. The beginning of the ruled surface is marked with a zero. For different views of this picture, we refer to Figure S4 of the Supporting Information. Three-dimensional representations of this study were rendered in the software VMD.²³ [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]