Abstract
We report an experimental validation and applications of the new hemodynamic model presented in the companion article (Fantini, 2013, this issue) both in the frequency domain and in the time domain. In the frequency domain, we have performed diffuse optical measurements for coherent hemodynamics spectroscopy (CHS) on the brain and calf muscle of human subjects, showing that the hemodynamic model predictions (both in terms of spectral shapes and absolute spectral values) are confirmed experimentally. We show how the quantitative analysis based on the new model allows for autoregulation measurements from brain data, and provides an analytical description of near-infrared spiroximetry from muscle data. In the time domain, we have used data from the literature to perform a comparison between brain activation signals measured with functional near-infrared spectroscopy (fNIRS) or with blood oxygenation level dependent (BOLD) fMRI, and the corresponding signals predicted by the new model. This comparison shows an excellent agreement between the model predictions and the reported fNIRS and BOLD fMRI signals. This new hemodynamic model provides a valuable tool for brain studies with hemodynamic-based techniques.
Keywords: Cerebral hemodynamics, coherent hemodynamic oscillations, cerebral autoregulation, functional near-infrared spectroscopy, functional magnetic resonance imaging, phasor analysis
1. Introduction
The objective of this work is to provide an experimental validation for the new hemodynamic model presented in the companion article (Fantini, 2013, this issue) both in the frequency domain and in the time domain. In the frequency domain, this hemodynamic model leads to a quantitative analysis of frequency-resolved measurements that are the basis for a novel technique called coherent hemodynamics spectroscopy (CHS) (Fantini, 2013, this issue). In the time domain, this hemodynamic model generates analytic expressions for signals that are measurable with hemodynamic-based neuroimaging techniques such as functional near-infrared spectroscopy (fNIRS) and functional magnetic resonance imaging (fMRI).
1.1. Hemodynamic oscillations
Cerebral hemodynamics feature spontaneous fluctuations over specific frequency bands associated with very-low-frequency oscillations (0.02-0.05 Hz) (Obrig et al., 2000), low-frequency oscillations (0.08-0.15) (Sassaroli et al., 2012), respiration (~0.2-0.3 Hz) (Zhang et al., 1998), and heart beat (~1 Hz) (Themelis et al., 2007). Furthermore, hemodynamic oscillations at a specific frequency can be induced by a number of protocols including paced breathing (Reinhard et al., 2006), head-up-tilting (Cheng et al., 2012), squat-stand maneuvers (Claassen et al., 2009), and pneumatic thigh-cuff inflation (Aaslid et al., 2007). It was reported that paced breathing induces hemodynamic oscillations that are characterized by a higher coherence than those associated with spontaneous breathing (Obrig et al., 2000; Reinhard et al., 2003). The high coherence of induced hemodynamic oscillations, together with the ability to control and vary their frequency, leads to the novel technique of coherent hemodynamics spectroscopy (CHS) that is proposed in the companion article (Fantini, 2013, this issue) and performed in this work for the first time.
Paced breathing has been used to induce hemodynamic oscillations at a specific frequency, typically ~0.1 Hz, to study cerebral autoregulation (Lang et al., 2001; Eames et al., 2004; Reinhard et al., 2006; Phillip et al., 2012), baroreflex sensitivity (Frederiks et al., 2000; Eames et al., 2004), effects of hypercapnia and brain activation (Obrig et al., 2000), and phase locking between physiological oscillations (Franceschini et al., 2006). Multiple paced breathing frequencies have been used to assess the effect of end-tidal CO2 on autoregulation [0.10, 0.17, 0.25 Hz (Eames et al., 2004)], possible overestimation of baroreflex sensitivity [0.10, 0.25 Hz (Frederiks et al., 2000)], and the frequency-dependence of locking among heart rate, blood pressure, and respiratory oscillations [0.10, 0.12, 0.17, 0.25, 0.50 Hz (Franceschini et al., 2006)].
A number of near-infrared spectroscopy (NIRS) studies have reported phase measurements for the oscillations in the tissue concentrations of deoxy-hemoglobin (D) and oxy-hemoglobin (O). For consistency, we have translated these literature measurements into the phase of D oscillations minus the phase of O oscillations. The phase difference between D and O oscillations associated with 0.10 Hz paced breathing was reported to be -260° (Obrig et al. 2000) and -200° (Reinhard et al., 2006) in healthy subjects, and -240° in patients with unilateral carotid obstruction (Reinhard et al., 2006). Reported phase differences between D and O oscillations associated with spontaneous low-frequency oscillations were -150° in the mouse brain [at 0.1 Hz (Lee et al., 2010)], -225° in the infant human brain 0.06-0.09 -234° [at ~0.09 Hz (Tian et al., 2011)] and -303° [at ~0.1 Hz (Obrig et al., 2000)] in the adult human brain at rest, and -285° [at ~0.08 Hz (Pierro et al., 2012)] in the adult human brain during deep sleep (when a higher coherence of low-frequency hemodynamic oscillations was observed). In this article, we present results that advance the study of hemodynamic oscillations with NIRS in two different ways. Firstly, we perform phase and amplitude measurements of D and O (from which one can derive the total hemoglobin concentration: T = D + O, and the hemoglobin saturation: S = O/T) at a number of discrete frequencies over the band 0.07-0.25 Hz. Such a richer data set, compared to measurements at a single frequency, allows for the characterization of the frequency dependence of the amplitude and phase of the measured oscillations. Secondly, we apply the novel hemodynamic model presented in the companion article (Fantini, 2013, this issue) for a quantitative analysis of the data and the measured spectral features. In the frequency domain, the new model uses a phasor representation of D, O, T, and S oscillations (Zheng et al., 2010; Pierro et al., 2012), which are considered as the outputs of a linear time invariant (LTI) system that describes the low-pass filter effects associated with the blood transit times in the capillary and venous compartments, as well as the high-pass filter effects associated with cerebral autoregulation. The input parameters of the model LTI system are oscillations in oxygen consumption, blood volume, and flow velocity, also represented with phasor notation. Specifically, in this work we have used a multi-frequency, paced-breathing protocol to perform coherent hemodynamics spectroscopy (CHS) on the brain and calf muscle of eleven human subjects. This study allowed us to investigate the inter-subject variability in the measured spectra and to demonstrate how the frequency-domain solution of the new hemodynamic model can be used to associate measured spectral features with underlying physiological processes such as cerebral autoregulation. We have found an excellent quantitative agreement between the CHS spectra measured in all eleven subjects and the frequency-domain solution of the new hemodynamic model.
1.2. Hemodynamic response to brain activation
Hemodynamic-based neuroimaging techniques such as functional near-infrared spectroscopy (fNIRS) and fMRI rely on changes in blood flow, blood volume, and blood oxygenation that are associated with brain activation. These hemodynamic changes result from a combination of focal brain activation effects and systemic physiological effects. The focal effects include changes in the metabolic rate of oxygen (CMRO2), cerebral blood volume (CBV), and cerebral blood flow (CBF) as a result of brain activation and neurovascular coupling. The systemic effects include changes in arterial blood pressure, heart rate, respiratory rate, etc., and associated cerebral autoregulation effects. Understanding the interplay between focal and systemic physiological, metabolic, and functional processes is a key requirement to fully characterize the BOLD fMRI signal (deoxy-hemoglobin content and blood volume) and the fNIRS signals (cerebral concentrations of oxy-hemoglobin and deoxy-hemoglobin). Hemodynamic models can play a key role in the study of the link between underlying physiological/functional/metabolic processes and the measured signals with functional neuroimaging techniques. A number of hemodynamic models have been developed on the basis of mass conservation for blood and diffusion-based oxygen extraction (for a review, see Buxton, 2012). In these models, blood volume and blood flow may be simply determined by the balance of inflow and outflow of blood for a vascular segment (Buxton et al., 1998), or they may be derived from resistive and compliance properties of blood vessels (Mandeville et al., 1999; Payne, 2006). These models typically include analytical relationships between flow and volume (Buxton et al., 1998; Kong et al., 2004), pressure and volume (Mandeville et al., 1999; Boas et al., 2008), or flow and oxygen extraction (Buxton et al., 1998; Hayashi et al., 2003). The new hemodynamic model (Fantini, 2013, this issue) is based on a different approach in that there are no assumptions of any relationships between flow, volume, and oxygen extraction, which instead are taken as independent inputs to the model. Furthermore, the model does not take the windkessel approach of finding an equivalent electrical circuit to describe blood flow and associated impedance characteristics. Instead, the idea is to conceptually follow blood circulation through the arterial, capillary, and venous compartments, and derive the time dependence of spatially averaged concentration and saturation of hemoglobin in tissue on the basis of (1) the blood transit time in the capillary and venous compartments, and (2) the rate constant of oxygen diffusion from capillary blood to tissue (Fantini, 2013, this issue). As a result, the new model is highly flexible in terms of its inputs [which may be any temporal perturbations in oxygen consumption, blood volume (separately for the arterial, capillary, and venous compartments), and flow velocity], and treats the complex microvascular network as a whole, by simply introducing three relevant parameters (the effective blood transit times in the capillary and venous compartments, and the rate constant for oxygen extraction from capillary blood).
In this work, we demonstrate the flexibility of the new model (Fantini, 2013, this issue) by deriving fNIRS and BOLD fMRI signals from experimental temporal traces of activation-induced perturbations in CBF, CBV, and CMRO2 reported in the literature. By using these experimental time traces as inputs to the model, we find an excellent agreement between the reported signals experimentally measured with fNIRS and fMRI and those predicted by the model.
2. Methods
2.1. Experimental methods for coherent hemodynamics spectroscopy (CHS)
Near-infrared spectroscopy (NIRS) measurements were performed with a commercial tissue oximeter (OxiplexTS, ISS, Inc., Champaign, IL) at a detection sampling rate of 6.25 Hz. The optical probes featured two illumination optical fibers (delivering light at two wavelengths, 690 and 830 nm) and one collection optical fiber bundle. The source-detector separation, i.e. the distance between the pair of illumination optical fibers and the collection fiber bundle, was 3.5 cm. The optical data, namely the diffuse optical intensities at 690 and 830 nm, were translated into deoxy-hemoglobin (D) and oxy-hemoglobin (O) concentrations by utilizing the modified Beer-Lambert law (Delpy et al., 1988; Sassaroli and Fantini 2004). On all eleven measured subjects, one optical probe was placed on the right side of the forehead and held in place by a flexible headband. In a subset of four subjects (Nos. 1, 2, 3, 6), we also collected data on the right calf muscle using a second optical probe. A black cloth was used to cover the optical probes to guarantee that room light could not reach the detector optical fiber. To continuously monitor respiration, we used a strain gauge placed around the subject’s chest, and we connected its analog output to an auxiliary input port of the tissue spectrometer for simultaneous recording with the optical data. A schematic diagram of the experimental setup is shown in Fig. 1.
Fig. 1.
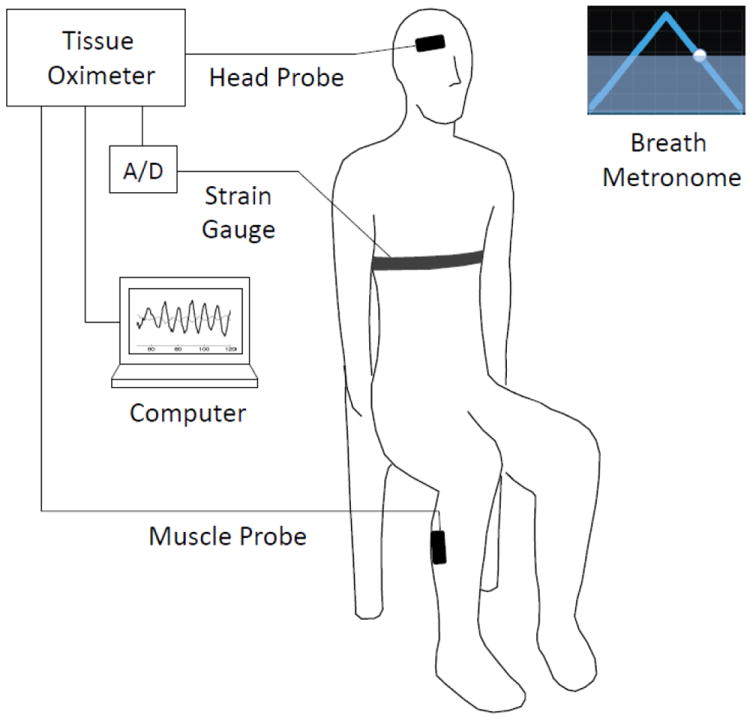
Schematic diagram of the experimental setup and protocol. Subjects were seated and performed paced breathing at specific frequencies within the range 0.07-0.25 Hz following the visual cue of a breath metronome (“Paced Breathing” Android™ application). Respiratory effort was monitored with a commercial strain gauge (Ambu Sleepmate Piezo Effort Sensor), digitized with an analog-to-digital converter (A/D), and displayed in real-time on a computer screen. Optical data were collected with optical probes placed on the right side of the subjects’ forehead (head probe) and right calf muscle (muscle probe). The optical probes were connected to a commercial tissue oximeter (OxiplexTS, ISS, Inc., Champaign, Illinois).
Eleven healthy adult volunteers (numbered 1-11), 5 males (subjects Nos. 1, 2, 3, 4, 6) and 6 females (subjects Nos. 5, 7, 8, 9, 10, 11), participated in the study. Average ± standard deviation of the subjects’ age was 32 ± 9 y. Five subjects (Nos. 1-5) performed paced breathing at eleven frequencies (0.071, 0.077, 0.083, 0.091, 0.100, 0.111, 0.125, 0.143, 0.167, 0.200, 0.250 Hz). In this case, there was an initial 30 s baseline acquisition, followed by a sequence of eleven 120 s paced breathing periods (one per each frequency) separated by 60 s of spontaneous breathing periods. The total measurement time for the eleven-frequency spectra was therefore ~33 min. Six subjects (Nos. 6-11) performed paced breathing at four frequencies (0.071, 0.100, 0.167, 0.250 Hz). In this case, there was an initial 2 min baseline period with spontaneous breathing, followed by a sequence of four 5 min paced breathing periods (one per each frequency) separated by 2 min of spontaneous breathing periods. The total measurement time for the four-frequency spectra was therefore 30 min. We observe that the relatively long measurement times used in this proof-of-principle study can be significantly shortened since we found that a few periods of paced breathing at each frequency are sufficient for accurate amplitude and phase hemodynamic measurements.
As a breathing metronome, we used the “Paced Breathing” Android™ application to guide the subjects through the inhalation and exhalation phases of paced breathing (see Fig. 1). Figure 2 displays a screen shot of the triangular breathing wave shown to the subjects, as well as the strain gauge signal that monitors the synchronous respiratory effort during paced breathing (at 0.1 Hz in the case of Fig. 2). This method helped the subjects to perform controlled paced breathing while following instruction to avoid breath holding and hyperventilation (all subjects were asked to maintain shallow breathing throughout the protocol). Each subject had a brief trial session under our supervision prior to the measurements in order to be trained to perform the paced breathing task correctly. The signal from the respiration strain gauge was also used as a real-time monitor of how well the paced breathing exercise was performed by the individual subjects. The experimental protocol was approved by the Tufts University Institutional Review Board (IRB) and written informed consent was obtained from all participants prior to the study.
Fig. 2.
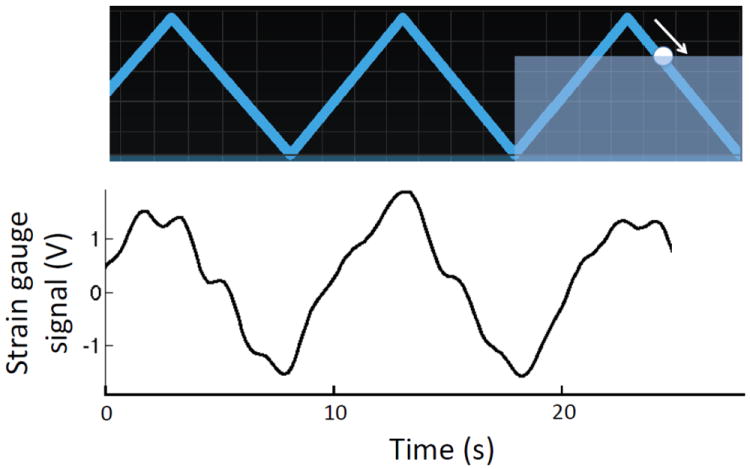
Illustration of the breathing metronome display as presented to the subject during paced breathing periods (top panel) and the corresponding strain gauge signal (bottom panel) collected on subject No. 3 during 0.1 Hz paced breathing. In this example, the moving circle (the arrow indicates its motion direction) is guiding the subject through the exhalation phase of paced breathing.
2.2. Data Analysis
2.2.1 Frequency-domain: coherent hemodynamics spectroscopy (CHS)
Slow temporal drifts were removed from all oxy-hemoglobin (O), deoxy-hemoglobin (D), and total hemoglobin (T) concentration traces by third-order polynomial detrending. The respiration belt signal is a continuously acquired voltage signal that reflects the subject’s respiratory effort and that is co-registered with NIRS data as described in Section 2.1. Coherence between the respiration belt signal and O was calculated with a built-in Matlab function (mscohere) during baseline (at the peak of the spontaneous respiration frequency band), and during paced breathing (at each of the paced breathing frequencies considered). Detrended D, O, and T temporal traces were then band-pass filtered by using a linear phase finite impulse response (FIR) filter based on the Parks–McClellan algorithm (Parks and McClellan, 1972). The filter center frequency was given by the paced breathing frequency, whereas its bandwidth was set to 0.02 Hz.
The band-pass filtered temporal traces of D(t) and O(t) were translated into frequency domain phasors D(ω) and O(ω) (Zheng et al., 2010) whose amplitude and phase were determined by analytic signal analysis (Gabor, 1946) as we have previously described (Pierro et al., 2012). The total hemoglobin concentration phasor T(ω) was then obtained by the phasor sum of the deoxy- and oxy-hemoglobin phasors, i.e. T(ω) = D(ω) + O(ω). The novel approach of coherent hemodynamics spectroscopy (CHS) (Fantini, 2013, this issue) is based on frequency-resolved measurements of the amplitude and phase of the hemoglobin concentration phasors D, O and T. In particular, we focus here on the amplitude ratios |D|/|O| and |O|/|T|, and on the phase differences Arg(D)-Arg(O) and Arg(O)-Arg(T). Instantaneous amplitude and phase values of D, O and T were obtained over the duration of each paced breathing task, resulting in associated mean values and standard deviations. Mean values and standard deviations for angular data were calculated by using circular statistics. Specifically, the angular standard deviation (in radians) was calculated as , where r is the magnitude of the resultant vector of the circular distribution of measured phase angles (Zar, 2010).
The novel hemodynamic model and its analytical expression for D, O and T, reported in the companion paper (Fantini, 2013, this issue), were used as a forward model to represent the coherent hemodynamics spectra. By assuming that paced breathing is not associated with significant synchronous cerebral oxygen consumption oscillations (null oxygen consumption phasor: ȯ = 0), the frequency-dependent phasor expressions for D, O and T are as follows (Fantini, 2013, this issue):
| (1) |
| (2) |
| (3) |
where the superscripts (a), (c), and (v) indicate the arterial, capillary, and venous compartments, respectively, for ϕ (blood volume fraction), S (hemoglobin saturation), t (blood transit time), v (blood volume phasor), and f(c) (flow velocity phasor). F(c) is the Fåhraeus factor (i.e. the ratio of capillary to large vessel hematocrit), ctHb is the concentration of hemoglobin in blood, αȯ is the rate constant of oxygen diffusion from blood to tissue, and, and are the transfer functions for the capillary (RC low-pass) and venous (Gaussian time-shifted low-pass) filters, respectively. We note that the hemoglobin concentration phasors O, D, T have absolute units of micromolar (as signified by the upper case notation), whereas blood volume (v(a), v(c), v(v)) and flow velocity phasors (f(c)) are dimensionless (as signified by the lower case notation) (Fantini, 2013, this issue). We introduce a relationship between flow and volume according to the high-pass filter model of autoregulation (Diehl et al., 1995) as follows:
| (4) |
where is the RC high-pass transfer function, and k is the asymptotic flow/volume amplitude ratio (which is related to the inverse of the modified Grubb’s exponent). The volume phasor (v) in Eq. (4) is in general a weighted average of the arterial, capillary, and venous volume phasors, and we consider here equal weights for the three compartments, so that v = (v(a) + v(c) + v(v))/3.
Equation (3) shows that the total hemoglobin phasor T is only affected by blood volume oscillations. In this work, we take the phase of volume oscillations (and therefore the phase of T) as the phase reference, so that Arg(T) = 0. By contrast, the deoxy- and oxy-hemoglobin phasors D and O result from the sum of two phasors. A first phasor is associated with volume oscillations, so that it has a zero phase, and has a different magnitude in the expressions for D and O. A second phasor is associated with flow velocity oscillations. Its phase results from negative phase contributions from the low-pass filter terms and , and positive phase contributions from the high-pass filter term [see Eq. (4)], and it has the same magnitude but opposite signs (or 180° phase difference) in the expressions for D and O.
To identify the best fits between the analytical expressions of Eqs. (1)-(4) and the measured coherent hemodynamics spectra, we have used a combination of manual parameter adjustments and a non-linear constrained fitting procedure (Matlab function lsqcurvefit). With the exception of ctHB, F(c), S(a), and αȯ, which we found to have negligible effects on the predicted spectra when varied within physiological ranges, we have modified all model parameters in our search for the best fits. Specifically, the fitting parameters were the capillary blood transit time (t(c)), the venous blood transit time (t(v)), the blood volume fractions (ϕ(a), ϕ(c), ϕ(v)), the blood volume phasors (v(a), v(c), v(v)), the high-pass autoregulation cutoff frequency and the asymptotic flow-to-volume amplitude ratio (k). The non-linear fitting procedure employed upper and lower constraints to fitted parameters based on assumed physiological/anatomical ranges.
2.2.2. Time domain: fNIRS and fMRI signals in response to brain activation
The hemodynamic model reported in the companion article (Fantini, 2013, this issue) also yields time-domain expressions for D(t) and O(t) that can be used to predict brain-activation signals measured with fNIRS and fMRI. The time-domain solutions of Fantini’s model, which are related to the frequency-domain solutions by Fourier transformation, lead to the following expressions for D(t) and O(t):
| (5) |
| (6) |
where the various parameters have already been defined in Eqs. (1)-(3), and instead of the phasors D, O, v(a), v(c), v(v), and f(c) that appear in Eqs. (1) and (2), Eqs. (5) and (6) contain the temporal functions D(t), O(t), v(a)(t), v(c)(t), v(v)(t), and f(c)(t). Similarly to the frequency-domain case, D(t) and O(t) have absolute units of micromolar, whereas v(a)(t), v(c)(t), v(v)(t), and f(c)(t) are dimensionless variations relative to background values. Furthermore, we have introduced the oxygen consumption ȯ (t) in Eqs. (5) and (6), and we have not assumed any relationship between flow and volume [as instead was done in the frequency-domain case via Eq. (4)]. The integrals in Eqs. (5) and (6) represent the convolutions of relative changes in flow velocity [f(c)(t)] and oxygen consumption [ȯ (t)] with the impulse response functions for the RC low-pass filter and the time-shifted Gaussian low-pass filter , which represent the low-pass effects of blood transit in the capillary and venous compartments, respectively.
The BOLD signal (SBOLD), which is measured in functional magnetic resonance imaging (fMRI) can also be determined by the model. SBOLD can be expressed in terms of the normalized voxel content of deoxy-hemoglobin (D(t)/D0, where D0 is the tissue concentration of deoxy-hemoglobin at baseline) and the normalized venous blood volume [1 + v(v)(t)] (Obata et al., 2004). If we modify the expression reported by Obata et al. (Obata et al., 2004) to consider all partially deoxygenated blood by introducing relative weights to the arterial, capillary, and venous compartments that reflect their deoxy-hemoglobin content, the BOLD signal can be written as follows (Fantini, 2013, this issue):
| (7) |
From a knowledge of the temporal shapes of the perturbations in blood volume [v(a) (t), v(c) (t), v(v) (t)], flow velocity [(f(c) (t)], and metabolic rate of oxygen [ȯ (t)], one can use Eqs. (5)-(7) to predict the absolute tissue hemoglobin concentrations D(t) and O(t), as well as the fMRI BOLD signal (SBOLD). We have used published data to evaluate the ability of Eqs. (5)-(7) to reproduce experimental fNIRS signals and BOLD fMRI signals. Two published studies have been chosen, one reporting fNIRS measurements and concurrent measurements of f(c) and ȯ (Durduran et al., 2004), and one reporting BOLD fMRI measurements as well as measurements of f(c) and v (Kida et al., 2007) (here, v represents the relative cerebral blood volume changes ΔCBV/CBV). The data reported in these manuscripts have been retraced and discretized to be used for the validation of Eqs. (5)-(7) in predicting fNIRS and BOLD fMRI signals. The methods from each of the two studies are briefly summarized here.
fNIRS study (Durduran et al., 2004)
Durduran et al. performed diffuse optical imaging and correlation spectroscopy on human subjects during sensorimotor stimulation. The sensorimotor stimulation was performed in a block design, with the subjects being instructed to tap the index and middle fingers against the thumb for 1 min at a frequency of 3 Hz. A 1-min rest period was recorded before and after each stimulus block. Simultaneous measurements of oxy-hemoglobin (O) and deoxy-hemoglobin (D) concentrations, as well as blood flow perturbations (f(c)) were reported. The perturbation in metabolic rate of oxygen (ȯ) was derived from the measured variation in blood flow, deoxy-hemoglobin concentration, and total hemoglobin concentration (Boas et al., 2003; Culver et al., 2003). The relative changes in f(c), ȯ and hemoglobin concentrations were corrected for partial volume effects. The results reported by Durduran et al. (Durduran et al., 2004) for f(c) and ȯ were complemented by our estimation of v on the basis of the reported relative changes in total hemoglobin concentration. We assumed the reported total hemoglobin changes to be proportional to the relative blood volume changes, and the proportionality factor, given by the total hemoglobin concentration in the activated tissue volume, was assumed to be 115 μM.
BOLD fMRI study (Kida et al., 2007)
Kida et al. performed fMRI experiments on rats involving different blocks of forepaw stimulation, with durations of 4, 8, 16, and 32 seconds (here, we consider the 4 s and 16 s forepaw stimulation blocks). All fMRI data were obtained on a modified 7.0 T horizontal-bore spectrometer. The goal of the study was to measure transient relationships between blood flow, blood volume, and BOLD signals with a temporal resolution of 500 ms. Transient blood flow changes (f(c)) were acquired with arterial spin labeling (ASL). Relative changes in blood volume (v) were measured by a super paramagnetic contrast agent after the f(c) and BOLD measurements were performed. We have complemented the results of Kida et al. (Kida et al., 2007), by deriving relative changes in metabolic rate of oxygen (ȯ) on the basis of the reported f(c), v, and BOLD changes, using the expression given by Hyder et al. (Hyder et al., 2001).
3. Results
3.1. Paced breathing induces coherent hemodynamic oscillations
Figure 3 shows representative data (collected on subject No. 3) of the strain gauge signal representing respiratory effort (Fig. 3A), and temporal variations in the cerebral tissue concentrations of oxy-hemoglobin (ΔO) and deoxy-hemoglobin (ΔD). The data in Fig. 3 have been de-trended but not band-pass filtered. The first minute in Fig. 3 refers to spontaneous breathing, whereas the second minute refers to 0.1 Hz paced breathing. The synchronization between ΔO, ΔD, and the strain gauge signal during paced breathing is evident, and this is reflected in a higher coherence between the respiratory signal (which represents an input physiological parameter for the new hemodynamic model) and the oxy-hemoglobin concentration (which represents an output parameter for the model). In fact, the coherence between the strain gauge signal and the unfiltered oxy-hemoglobin concentration was consistently higher during paced breathing than during spontaneous breathing. For all investigated subjects, we found coherence values at the peak of the spontaneous respiratory frequency band (~0.25-0.40 Hz) to be within the range 0.06-0.84. For all subjects and all paced breathing frequencies, we found higher coherence values at the paced breathing frequency within the range 0.85-1.00.
Fig. 3.
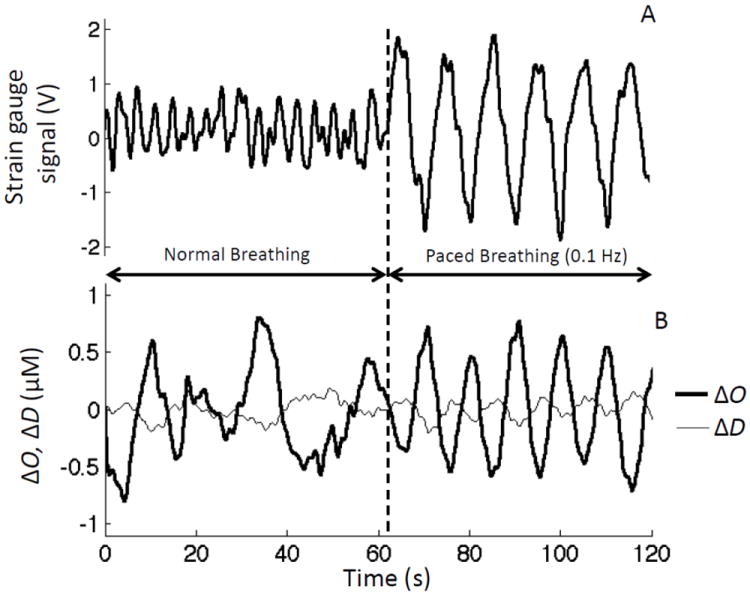
(A) Strain gauge signal used to monitor respiratory effort, and (B) temporal traces of changes in the concentrations of oxy-hemoglobin (ΔO) and deoxy-hemoglobin (ΔD) during 60 s baseline (normal breathing), and 60 s of paced breathing at 0.1 Hz.
3.2. Coherent hemodynamics spectroscopy (CHS)
We report frequency-resolved measurements of the amplitude ratios |D|/|O| and |O|/|T|, and of the phase differences Arg(D)-Arg(O) and Arg(O)-Arg(T) during paced breathing. These frequency-resolved measurements realize the newly proposed technique of coherent hemodynamics spectroscopy (CHS) (Fantini, 2013, this issue).
3.2.1. Brain measurements
The amplitude and phase spectra measured on the forehead of subject No. 3 are reported in Figs. 4A-D, and representative phasor diagrams at 0.2 Hz are shown in Figs. 4E-F. The symbols in Figs. 4A-D are the measured data points, whereas the lines represent the fits with the hemodynamic model equations [Eqs. (1)-(4)]. The theoretical spectra of Figs. 4A-D, which show an excellent agreement with the experimental data, highlight some basic features of the amplitude-ratio and phase-difference spectra considered here.
Fig. 4.
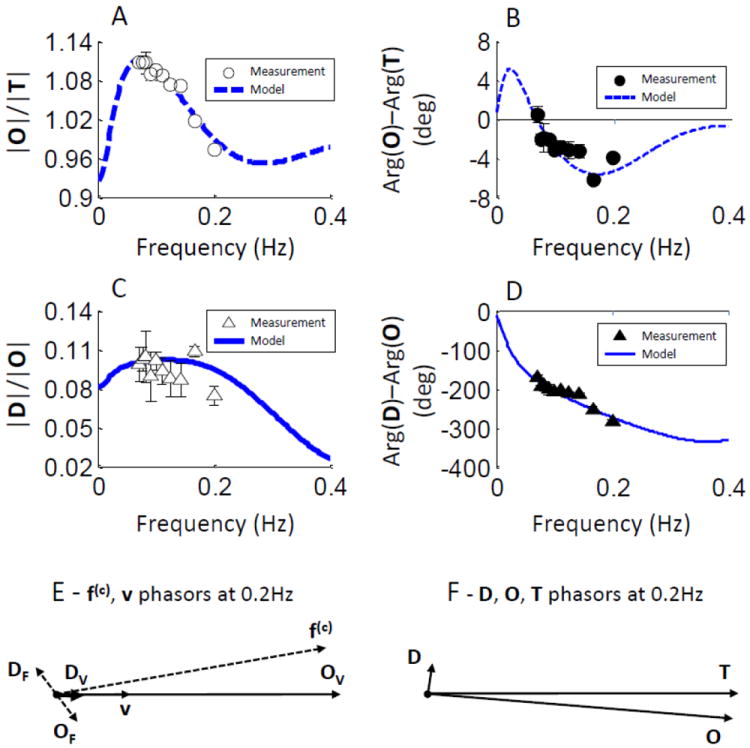
Representative CHS spectra measured on the forehead of subject No. 3 and associated phasor diagrams (at 0.2 Hz) on the basis of measured deoxy-hemoglobin (D), oxy-hemoglobin (O), and total hemoglobin (T) phasors. (A) Amplitude ratio |O|/|T|, (B) phase difference Arg(O)-Arg(T), (C) amplitude ratio |D|/|O|, (D) phase difference Arg(D)-Arg(O). Symbols represent experimental data (error bars are standard deviations), whereas the lines represent the best fits obtained with the hemodynamic model. The phasor diagrams for 0.2 Hz oscillations, as obtained with the hemodynamic model, are reported in panel (E) for the flow velocity (f(c)), blood volume (v), and associated hemoglobin concentration phasors (DF, OF, DV, OV), and in panel (F) for the tissue concentrations of deoxy-hemoglobin (D), oxy-hemoglobin (O), and total hemoglobin (T). Notice that while DV and OV (the hemoglobin oscillations determined by blood volume oscillations) are in phase with v, DF and OF (the hemoglobin oscillations determined by flow velocity oscillations) are not in phase with f(c).
Notable spectral features
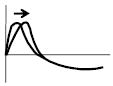
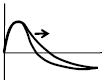
Figs. 4A and 4C show the amplitude-ratio spectra |O|/|T| and |D|/|O|, respectively. Key features of the |O|/|T| spectrum are the peak value (~1.11 in Fig. 4A) and the peak frequency (~0.07 Hz in Fig. 4A). Key features of the |D|/|O| spectra are the peak value (~0.1 in Fig. 4C) and whether the peak concavity is positive (convex spectrum), close to zero (linear spectrum), or negative (concave spectrum, the case of Fig. 4C).
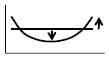
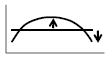
Figs. 4B and 4D show the phase-difference spectra Arg(O)-Arg(T) and Arg(D)-Arg(O), respectively. Key features of the Arg(O)-Arg(T) spectrum are the peak values of the positive and negative peaks (~±5° in Fig. 4B), the positive peak frequency (~0.025 Hz in Fig. 4B), and the zero-crossing frequency (~0.07 Hz in Fig. 4B). Key features of the Arg(D)-Arg(O) spectrum are the phase value around 0.1 Hz (~-200° in Fig. 4D), and the phase slope within a frequency band centered at 0.1 Hz (~0.8°/mHz in Fig. 4D).
Table I reports a visual summary of the key spectral features described above, and specifies how they are affected by each one of the model parameters that we have used as fitting parameters as described in Section 2.2.1. We observe that some of the effects reported in Table I [which apply to the case of the reference set of parameters values given in Table II of the companion article (Fantini, 2013, this issue)] do not hold in general, and may even be reversed under particular conditions. Nevertheless, Table I provides a valuable reference to guide the interpretation of the measured coherent hemodynamics spectra.
Table I.
Summary of the effects of the hemodynamic model parameters on the CHS spectral features of hemoglobin concentration phasors (D, O, T) within the frequency band 0 - 0.3 Hz. The arrows indicate whether an increase (↑) or decrease (↓) of each parameter induces the spectral change reported in the left column.
| Spectral features in the 0-0.3 Hz frequency band | ϕ(a) | ϕ(c) | ϕ(v) | t(c) | t(v) |
|
k | |v(a)| | |v(c)| | |v(v)| | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
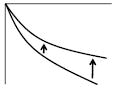
|
Phase increase of Arg(D)-Arg(O) (i.e. less negative) | ↑ | ↓ | ↓ | ↓ | ↑ | ↓ | ↓ | ↑ | |||
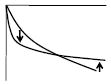
|
Shallower phase slope of Arg (D)-Arg(O) | ↑ | ↓ | ↓ | ↓ | ↓ | ↑ | ↑ | ↓ | |||
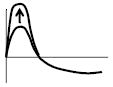
|
Peak amplitude increase of positive peak of Arg (O)-Arg(T) | ↓ | ↑ | ↑ | ↑ | ↓ | ||||||
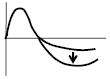
|
Absolute peak amplitude increase of negative peak of Arg (O)-Arg(T) | ↓ | ↓ | ↑ | ↑ | ↓ | ↑ | ↓ | ||||
|
Peak frequency increase of positive peak of Arg (O)-Arg(T) | ↑ | ||||||||||
|
Zero-crossing frequency increase of Arg (O)-Arg(T) | ↑ | ↓ | ↓ | ↓ | ↑ | ||||||

|
Increase of |D|/|O| | ↓ | ↑ | ↓ | ↓ | ↑ | ↑ | ↓ | ||||
|
Convex spectrum of |D|/|O| | ↓ | ↑ | ↑ | ↓ | ↑ | ↑ | |||||
|
Concave spectrum of |D|/|O| | ↑ | ↑ | |||||||||

|
Peak amplitude increase of |O|/|T| | ↓ | ↑ | ↓ | ↓ | ↑ | ↑ | ↓ | ||||

|
Peak frequency increase of |O|/|T| | ↑ | ↓ | ↓ | ↓ | ↑ | ||||||
Table II.
Values of the model parameters obtained by fitting the hemodynamic model equations to the CHS spectra measured on the forehead of eleven human subjects.
| Parameter | Common values |
|---|---|
| ctHB (mM) | 2.3 |
| F(c) | 0.8 |
| S(a) | 0.98 |
| αȯ (s-1) | 0.8 |
| Individual measured values on the eleven subjects | ||||||||||||
|
| ||||||||||||
| Subject No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|
| ||||||||||||
| t(c) (s) | 0.87 | 0.87 | 0.56 | 0.75 | 0.5 | 0.87 | 0.75 | 0.62 | 0.87 | 0.87 | 0.5 | |
| 5 | 5 | 5 | 5 | 5 | 5 | |||||||
| t(v) (s) | 1 | 2.2 | 2.6 | 1 | 2.3 | 2.5 | 2.8 | 2.6 | 2.6 | 2.3 | 2.2 | |
| ϕ(a) | 0.00 | 0.01 | 0.01 | 0.01 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 | 0.01 | |
| 4 | 3 | 6 | 5 | 1 | 2 | 6 | 3 | 6 | 5 | 5 | ||
| ϕ(c) | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.01 | 0.01 | 0.01 | 0.00 | |
| 1 | 7 | 4 | 4 | 4 | 7 | 3 | 6 | 1 | 5 | 5 | ||
| ϕ(v) | 0.01 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0 | 3 | 3 | 4 | 7 | 7 | 4 | 6 | 7 | 5 | 3 | ||
| |v(a)| | 0.01 | 0.04 | 0.04 | 0.05 | 0.01 | 0.02 | 0.02 | 0.04 | 0.02 | 0.01 | 0.04 | |
| 5 | 5 | 5 | ||||||||||
| |v(c)| | 0.02 | 0.03 | 0.04 | 0.06 | 0.01 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | |
| 1 | 5 | |||||||||||
| |v(v)| | 0.02 | 0.02 | 0.02 | 0.05 | 0.00 | 0.01 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | |
| 5 | 5 | 5 | 5 | 5 | ||||||||
|
|
0.08 | 0.03 | 0.03 | 0.00 | 0.13 | 0.07 | 0.00 | 0.06 | 0.07 | 0.04 | 0.02 | |
| 7 | 7 | 5 | 5 | 5 | 5 | 7 | 5 | |||||
| k | 3.8 | 4.2 | 4.1 | 2.5 | 5 | 3.7 | 8 | 3.5 | 5 | 5.6 | 5.2 | |
Phasor diagrams
Figures 4E-F report the phasor diagrams obtained at 0.2 Hz from the fit of the model to the experimental data (as shown in Figs. 4A-D). The blood volume (v) and flow velocity (f(c)) phasors are shown in Fig. 4E on the same scale, so that one can appreciate the larger magnitude of f(c) versus v (by a factor of ~4 in this case). The blood volume phasor v (which is the average of v(a), v(c), and v(v) as described in relation to Eq. (4) above) is obtained from the model fit to the experimental data, and the flow velocity phasor f(c) is then obtained from Eq. (4) using the fitted values of k (4.1 in this case) and (0.035 Hz in this case). The deoxy-hemoglobin and oxy-hemoglobin concentration phasors associated with v (DV, OV) and f(c) (DF, OF), as given by the first and second terms, respectively, of Eqs. (1) and (2), are also shown in Fig. 4E, from which one can observe that while volume oscillations induce in-phase (synchronous with v) hemoglobin oscillations, flow velocity oscillations induce, in general, out-of-phase (delayed with respect to f(c)) hemoglobin oscillations. The resultant deoxy-hemoglobin (D = DF + DV), oxy-hemoglobin (O = OF + OV), and total hemoglobin (T = D + O) concentration phasors reported in Fig. 4F show that T is in phase with volume oscillations, while D and O are, in general, out-of-phase with each other.
Fitting the measured spectra using the hemodynamic model
The hemodynamic model involves two time constants, namely τ(c) = t(c)/e and , which reflect the low-pass filter response of the capillary and venous saturation, respectively, to changes in the blood flow velocity (and oxygen consumption) (Fantini, 2013, this issue). These two time constants correspond to the two low-pass cutoff frequencies and , respectively (Fantini, 2013, this issue). A third, high-pass cutoff frequency describes the autoregulation, high-pass response of blood flow velocity to changes in blood volume (according to the transfer function of Eq. (4)). The interplay of these three cutoff frequencies plays a crucial role in determining the spectral features measured with coherent hemodynamics spectroscopy. Physiological ranges of these three cutoff frequencies are in the order of 0.4-1.2 Hz for , 0.2-1.0 Hz for , and 0-0.2 Hz for (for which a zero value indicates a lack of autoregulation), and are therefore within or just outside the range of paced-breathing frequencies considered here (0.07-0.25 Hz). The effects of t(c), t(v), and , as well as other relevant model parameters, on a number of spectral features of the phase and amplitude spectra of hemoglobin concentration phasors are summarized in Table I. We observe that frequency shifts (of the peak frequency and zero crossing frequency of Arg(O)-Arg(T), and the peak frequency of |O|/|T|) all mostly depend on t(c), t(v), and , as well as ϕ(c) and ϕ(v), which determine the relative weights of the capillary and venous low-pass filter contributions (see Table I).
The considerations above and the guiding information of Table I have been used to perform an initial manual adjustment of the model parameters to fit the experimental data using Eqs. (1)-(4). The set of parameter values obtained with this initial manual adjustment was used as the initial set of values for a nonlinear fitting procedure to improve the fit quality, and to identify the final set of model parameters associated with the measured CHS spectra. The results of the fits, which are reported in Fig. 5 for all subjects, show that the new hemodynamic model was able to reproduce the measured CHS spectra on all eleven subjects both qualitatively and quantitatively. The only exception is possibly the |D|/|O| spectral shape for subject No. 5. The excellent agreement between model and experimental results is particularly evident in the case of Fig. 4, where not only are the peak frequency of |O|/|T|, the zero-crossing frequency of Arg(O)-Arg(T), and the overall experimental spectral shapes reproduced, but it is remarkable that the absolute values of |O|/|T|, |D|/|O|, Arg(O)-Arg(T), and Arg(D)-Arg(O) are all closely reproduced by the new hemodynamic model. We stress that the fits did not include any adjustable scaling factor, so that the comparison between the model predictions of the experimental spectra applies to both the spectral shape and the absolute spectral values.
Fig. 5.
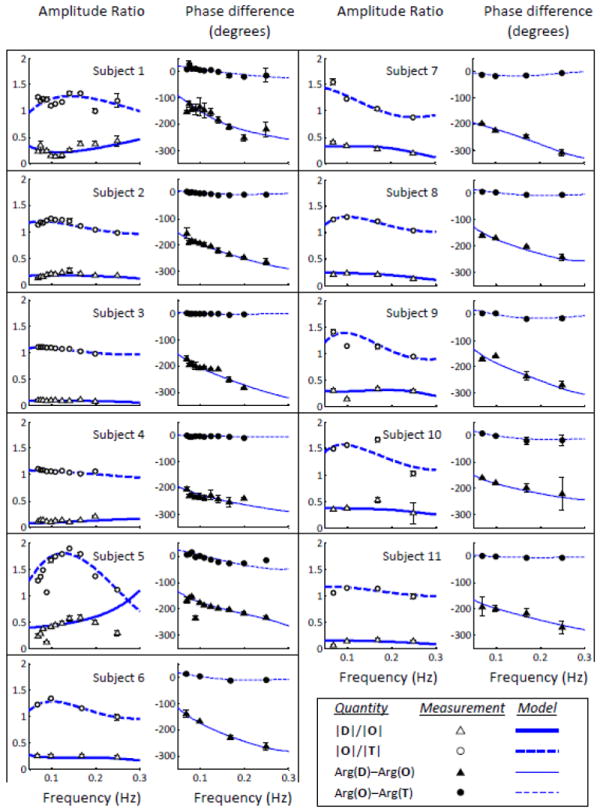
Measured CHS spectra on the forehead of all eleven subjects (symbols), and best fits with the hemodynamic model (lines) for all eleven subjects. For each subject, the left panel shows the amplitude ratio spectra (|O|/|T| and |D|/|O|), and the right panel shows the phase difference spectra (Arg(O)-Arg(T) and Arg(D)-Arg(O)).
The values of the fitting parameters corresponding to the CHS spectra of Fig. 5 are reported in Table II for all eleven subjects. As mentioned in the methods section 2.2.1, we have considered constant values (given in Table II) for ctHB, F(c), S(a), αȯ, and the fitting parameters were the capillary blood transit time (t(c)), the venous blood transit time (t(v)), the blood volume fractions (ϕ(a), ϕ(c), ϕ(v)), the blood volume phasors (v(a), v(c), v(v)), the high-pass autoregulation cutoff frequency and the asymptotic flow/volume amplitude ratio (k). Over the eleven subjects, t(c) ranges from 0.5-0.875 s, whereas t(v) ranges from 1-2.8 s. Assuming a capillary blood velocity of 0.8 mm/s, the measured t(c) values indicate red blood cells pathlengths within capillaries of 400-700 μm, which are consistent with capillary segment lengths reported in Table I and in the introduction of the companion article (Fantini, 2013, this issue). Assuming a venous blood velocity of 1 mm/s, the measured t(v) values indicate venous lengths of 1-2.8 mm, longer than typical venules since t(v) reflects transit times down the venule as well as larger veins in the venous system within the probed tissue volume. The measured arterial, capillary, and venous blood volume fractions (ϕ(a),ϕ(c), ϕ(v)) reflect different distributions of arterial and venous contributions in the eleven subjects, with a greater venous contribution (i.e. ϕ(v) > ϕ(a)) for subjects Nos. 1, 5, 6, 8, 9, and a greater arterial contribution (i.e. ϕ(v) < ϕ(a)) for subjects Nos. 2, 3, 4, 7, 11 (for subject No. 10, ϕ(v) = ϕ(a)). We have found an excellent correlation between the relative venous/arterial compartment contributions, and the autoregulation cutoff frequency . Specifically, subjects with ϕ(v) < ϕ(a) show lower values of , (<0.04 Hz), with respect to subjects with ϕ(v) > ϕ(a) for whom is in the range 0.06-0.13 Hz (subject No. 10, for which ϕ(v) = ϕ(a), has an of ~0.05 Hz, which falls in between the ranges for the other two groups). Such a good correlation between the relative venous and arterial contributions [expressed by the ratio (ϕ(v) – ϕ(a))/(ϕ(a) + ϕ(c) + ϕ(v))] and the autoregulation cutoff frequency is illustrated in Fig. 6. The autoregulation cutoff frequencies for the eleven subjects ranges from 0.005 Hz (indicating a lack of autoregulation) to 0.13 Hz [which is close to a reported typical value of 0.15 Hz (Blaber et al., 1997)]. We have not found a strong sensitivity of the CHS spectra on the amplitudes of the blood volume phasors v(a), v(c), v(v) (their phase is set to zero as they are taken as the phase reference), which are always in the order of a few percent. Finally, the asymptotic flow/volume amplitude ratio (k) for the eleven subjects is in the range 2.5-8, so that the range of values for its inverse (0.125-0.4) is in agreement with the range of values of the Grubb’s exponent reported in the literature (Leung et al., 2009, and references therein).
Fig. 6.
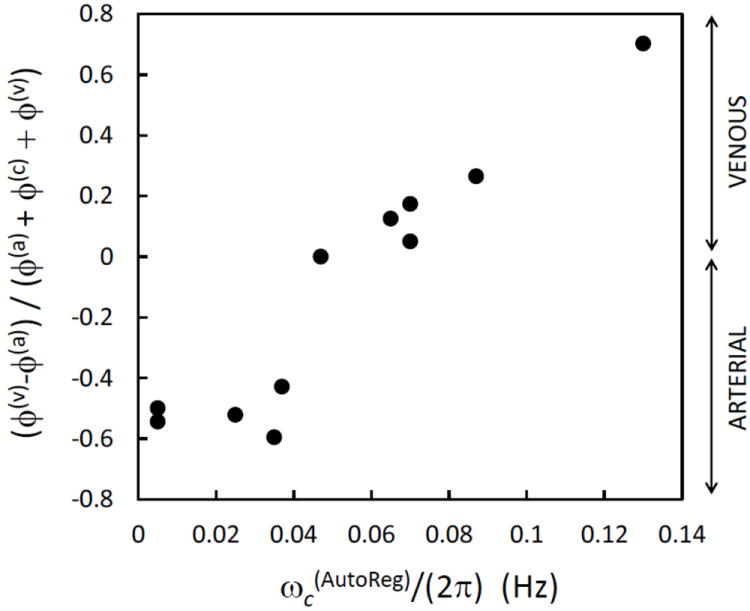
Correlation between the difference (ϕ(v) – (ϕ(a)) of venous and arterial partial volumes (normalized to the total blood partial volume) and the autoregulation cutoff frequency . The eleven points correspond to the measurements on the forehead of the eleven subjects, according to the parameter values given by the fits of the model equations to the measured CHS spectra (as reported in Table II).
3.2.2. Calf muscle measurements
We have also performed coherent hemodynamics spectroscopy (CHS) on the calf muscle of subjects Nos. 1, 2, 3 and 6. By contrast with brain measurements, we have found that amplitude ratio and phase difference spectra on the calf muscle do not show a frequency dependence. In particular, D, O, and T are in phase with each other at all frequencies. Therefore, we report in Fig. 7 the average over the four subjects of the four-point spectra (0.071, 0.100, 0.167, 0.250 Hz) of Arg(D)-Arg(O) and (|O|/|T|) measured on the calf muscle. Because the oscillations of oxy-hemoglobin and deoxy-hemoglobin concentrations are in phase with each other (Fig. 7A), the amplitude ratio of the oxy-hemoglobin to total hemoglobin oscillation represents the hemoglobin saturation of the volume-oscillating vascular compartment, which, at the respiratory frequency, is the venous compartment according to near-infrared spiroximetry (Franceschini et al., 2002). In our measurements, we found an average value of |O|/|T| of ~0.75, which is consistent with the venous saturation values (0.7-0.8) measured on the vastus medialis muscle with near-infrared spiroximetry (Franceschini et al., 2002). As discussed in the companion article (Fantini, 2013, this issue), this result of in-phase oscillations of D, O, and T, requires that the zero-phase contribution from the volume phasor term in Eqs. (1) and (2) dominate the frequency-dependent phase contribution of the flow velocity phasor term.
Fig. 7.
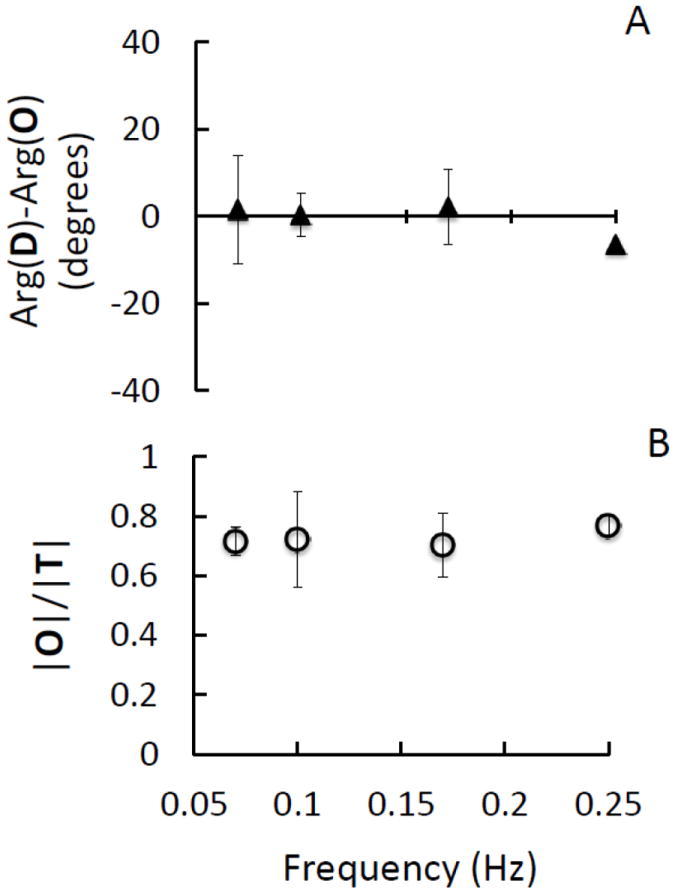
Calf muscle measurements at four paced-breathing frequencies (0.071, 0.100, 0.167 and 0.250 Hz). CHS spectra representing the average (symbols) and standard deviation (error bars) of the spectra measured on the calf muscle of four subjects (Nos. 1, 2, 3, 6). (A) Phase difference spectra of Arg(D)-Arg(O); (B) Amplitude ratio spectra of |O|/|T|.
3.3. Functional brain studies
fNIRS study
The input parameters for the hemodynamic model, namely f(c), ȯ, and v, obtained from Durduran et al. (Durduran et al., 2004) as described in section 2.2.2 are shown in Fig. 8. It was assumed that the relative volume change is the same in all vascular compartments, hence v(a)=v(c)=v(v)=v. Temporal courses of oxy-hemoglobin (O) and deoxy-hemoglobin (D) concentrations were calculated using Eqs. (5) and (6), where we have introduced the typical model parameter values reported in Table II of the companion article (Fantini, 2013, this issue). Figure 8 shows the relative changes ΔO and ΔD based on the hemodynamic model (dashed lines) as well as the measured values reported by Durduran et al. (Durduran et al., 2004) (solid lines). The agreement between the predictions of the hemodynamic model and the measured ΔO and ΔD traces is excellent both in shape and magnitude. In fact, the maximum deviations between model and experiment are ~±3 μM for ΔO and ~±0.5 μM for ΔD.
Figure 8.
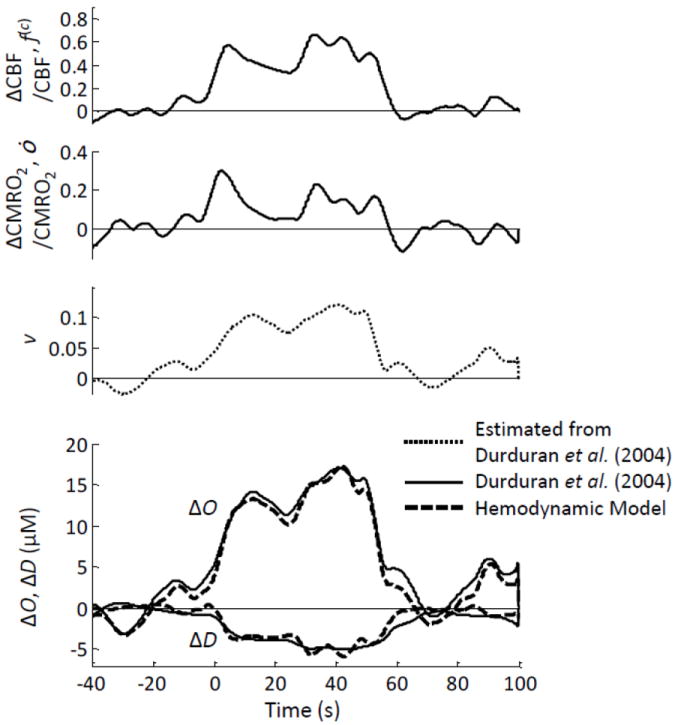
fNIRS study on human subjects during sensorimotor stimulation. The top three panels are the relative changes in cerebral blood flow (ΔCBF/CBF, f(c)), metabolic rate of oxygen (ΔCMRO2/CMRO2, ȯ), and blood volume (v) derived from the data reported by (Durduran et al., 2004) as described in the text. The bottom panel shows the oxy-hemoglobin and deoxy-hemoglobin concentration changes (ΔO and ΔD) measured by (Durduran et al., 2004) using fNIRS (solid line), and those predicted by the hemodynamic model (dashed lines).
We observe that because we have obtained the relative volume changes from the total hemoglobin traces reported by Durduran et al. (Durduran et al., 2004), by definition we obtain a perfect match between model and experiment for the total hemoglobin concentration (which is not shown in Fig. 8, being just the sum of ΔO + ΔD). However, the flow velocity and oxygen consumption terms in Eqs. (5) and (6) are the ones that determine the relative contributions of O and D, to the total hemoglobin concentration T, and they accurately predict the experimental traces by taking a reasonable value of 115 μM for the cerebral T value at the activated cortical area.
BOLD fMRI study
The input parameters for the hemodynamic model, namely f(c), ȯ and v, obtained from Kida et al. (Kida et al. 2007) as described in section 2.2.2 are shown in Fig. 9 for two stimulus durations (4 s and 16 s). Relative volume changes were assumed to be the same in all compartments, i.e. v(a)=v(c)=v(v)=v. The BOLD signal was calculated using Eq. (7), where we have introduced the typical model parameter values reported in Table II of the companion article (Fantini, 2013, this issue). The best agreement between the BOLD signal derived using the hemodynamic model [i.e. Eq. (7)] and the measured BOLD signal reported by Kida et al. (Kida et al. 2007) was achieved by using a value of 0.11 for the scaling factor Á, which is the physiological and magnetic field dependent constant that determines the relative contributions of f(c) and v to ȯ (Hyder et al., 2001). Figure 9 shows the BOLD signal calculated with the hemodynamic model (dashed lines), as well as the BOLD signal measured by Kida et al. (Kida et al., 2007) (solid lines). The calculated BOLD traces closely match the measured ones in terms of both shape and magnitude, except that the model predicts a slightly delayed onset in the BOLD signal.
Figure 9.
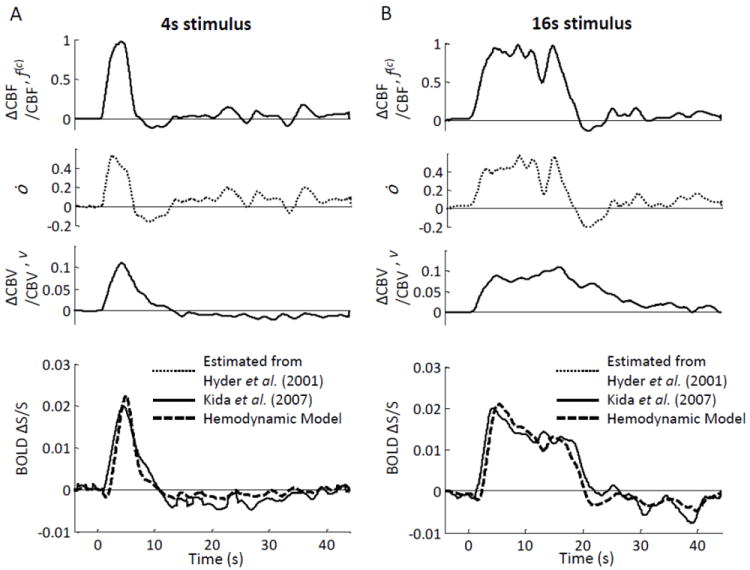
BOLD fMRI study on rats. (A) 4 s forepaw stimulation; (B) 16 s forepaw stimulation. The top three panels in (A) and (B) are the relative changes in cerebral blood flow (ΔCBF/CBF, f(c)), metabolic rate of oxygen (ȯ), and cerebral blood volume (ΔCBV/CBV, v) derived from the data reported by (Kida et al., 2007) as described in the text. The bottom panel in (A) and (B) shows the BOLD fMRI signal (ΔS/S) measured by (Kida et al., 2007) using fMRI (solid line), and those predicted by the hemodynamic model (dashed lines).
4. Discussion
This article has reported an experimental validation and applications of the new hemodynamic model presented in the companion article (Fantini, 2013, this issue). Both frequency-domain and time-domain solutions of the hemodynamic model have been considered.
In the frequency domain, frequency-resolved measurements of coherent hemodynamic oscillations induced by paced breathing were performed according to the newly proposed technique of coherent hemodynamics spectroscopy (CHS) (Fantini, 2013, this issue). The validation study on eleven subjects has demonstrated the ability of the new hemodynamic model to accurately reproduce the measured CHS spectra, and to identify relevant physiological parameters associated with them. The set of fitting parameters reported in Table II may be further refined by employing a more sophisticated fitting procedure for the determination of global minima for the fit residuals in the parameter space. Two major results are a broad range of autoregulation cutoff frequencies measured over the eleven subjects , and the strong correlation between and the relative venous/arterial contributions to the hemodynamic oscillations (see Fig. 6). The broad range of values indicates a distribution of cases from a lack of autoregulation to good autoregulation . Such a distribution of cases among the eleven subjects may be associated with differences in the specific investigated brain areas, differences in the relative venous/arterial partial volumes over the measured tissue regions, and/or differences in the relative contributions from cerebral and extracerebral tissue to the optical measurements. The present study is unable to identify the specific source of the correlation reported in Fig. 6, but the analytical tool provided by the new hemodynamic model lends itself to further investigations of this issue. It is worth noting that the physiological parameters introduced by us to describe autoregulation in Eq. (4), namely the capillary blood flow velocity and the microvasculature blood volume, are related to but not the same as the quantities typically used to describe autoregulation (i.e. blood flow and arterial blood pressure). As a result, our assessment of autoregulation may reflect microcirculation and vascular compliance effects, which may contribute to the large variability in the observed autoregulation cutoff frequencies reported in Table II and to the findings reported in Fig. 6.
In the time domain, the predictions of the model for cerebral hemodynamic perturbations associated with brain activation were found to agree well with reported brain activation signals measured with fNIRS and BOLD fMRI. Fantini’s model does not require any assumptions for the relationships among the input parameters, namely f(c), v(a), v(c), v(v), and ȯ, which are treated independently from each other. As a result, one can use the model to study the sensitivity of the fNIRS and BOLD fMRI signals to any of the input parameters, or, conversely, to identify the set of input parameters that is consistent with measured fNIRS or fMRI signals. It is important to observe that it is not just the magnitude of the input parameters that is modeled here, but their detailed temporal dynamics as well (for example: onset time, rise dynamics, overshoot/plateau level, decay dynamics, undershoot, etc.). In this respect, we observe that the temporal dynamics of the fNIRS and fMRI signals appear to be mostly dependent on the temporal evolution of the physiological inputs (oxygen consumption, blood volume, flow velocity), especially if they occur on a time scale that is significantly longer than the time constants of the microvascular impulse response functions [as determined by the blood transit times in the capillaries (t(c)) and veins t(v)]. However, other model parameters, especially the blood transit times (t(c), t(v)) and the blood volume fractions (ϕ(a), ϕ(c), ϕ(v)), do affect the model predictions as well and may be included in a fit of the model predictions to experimental hemodynamic neuroimaging signals. We have verified that the model predictions for the fNIRS and fMRI signals reported in Figs. 8 and 9, which are based on the typical parameter values reported in Table II of the companion paper (Fantini, 2013, this issue), are more strongly sensitive to the relative arterial/capillary/venous volume fractions than to the capillary and venous blood transit times, at least within the range of values observed in the eleven subjects of the paced breathing study (as reported in Table II of this article).
5. Conclusions
We have presented an experimental validation of a new hemodynamic model that can provide a valuable analytical tool for the newly proposed technique of coherent hemodynamics spectroscopy (CHS) and for functional brain studies based on fNIRS or fMRI. The results presented here are based on a novel hemodynamic model and on a new set of frequency-resolved measurements of hemodynamic oscillations that have been proposed for the first time in the companion article (Fantini, 2013, this issue) and that have been performed for the first time in this work. In this perspective, we are presenting initial findings using newly proposed methods. Future research will need to address a number of questions on the characterization and optimization of experimental protocols for the collection of CHS spectra, the refinement of fitting procedures to recover the model physiological parameters, the assessment of the reliability and reproducibility of the measurements of these parameters, the normal range of their values, and the identification of the potential of the proposed methods in research areas, medical diagnostics, and cerebral hemodynamic monitoring. Because of the critical importance of a quantitative spatio-temporal assessment of cerebral hemodynamics in research (functional brain imaging, neurovascular coupling, resting state functional connectivity, etc.) and clinical practice (stroke, traumatic brain injury, neurovascular disorders, anesthesia, hemodialysis treatment, etc.), the proposed methods may find applications in a variety of research and clinical areas.
Highlights.
We have validated a novel hemodynamic model in the frequency and time domains.
Frequency domain: Coherent Hemodynamics Spectroscopy (CHS) on brain and muscle.
Shape and absolute values of CHS spectra are accurately described by the model.
CHS spectra yield measures of autoregulation and other physiological parameters.
In the time domain, the model accurately predicts fNIRS and BOLD fMRI signals.
Acknowledgments
This research is supported by the National Institutes of Health (Grants No. R03-MH093846 and R01-CA154774) and by the National Science Foundation (Award No. IIS-1065154).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aaslid R, Blaha M, Sviri G, Douville CM, Newell DW. Asymmetric dynamic cerebral autoregulatory response to cyclic stimuli. Stroke. 2007;38:1465–1469. doi: 10.1161/STROKEAHA.106.473462. [DOI] [PubMed] [Google Scholar]
- Blaber AP, Bondar RL, Stein F, Dunphy PT, Moradshahi P, Kassam MS, Freeman R. Transfer function analysis of cerebral autoregulation dynamics in autonomic failure patients. Stroke. 1997;28:1686–1692. doi: 10.1161/01.str.28.9.1686. [DOI] [PubMed] [Google Scholar]
- Boas DA, Strangman G, Culver JP, Hoge RD, Jasdzewski G, Poldrack RA, Rosen BR, Mandeville JB. Can the cerebral metabolic rate of oxygen be estimated with near-infrared spectroscopy? Phys Med Biol. 2003;48:2405–2418. doi: 10.1088/0031-9155/48/15/311. [DOI] [PubMed] [Google Scholar]
- Boas DA, Jones SR, Devor A, Huppert TJ, Dale AM. A vascular anatomical network model of the spatio-temporal response to brain activation. NeuroImage. 2008;40:1116–1129. doi: 10.1016/j.neuroimage.2007.12.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buxton RB, Wong EC, Frank LR. Dynamics of blood flow and oxygenation changes during brain activation: The balloon model. Magn Res Med. 1998;39:855–864. doi: 10.1002/mrm.1910390602. [DOI] [PubMed] [Google Scholar]
- Buxton RB. Dynamic models of BOLD contrast. NeuroImage. 2012;62:953–961. doi: 10.1016/j.neuroimage.2012.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng R, Shang Y, Hayes D, Jr, Saha SP, Yu G. Noninvasive optical evaluation of spontaneous low frequency oscillations in cerebral hemodynamics. NeuroImage. 2012;62:1445–1454. doi: 10.1016/j.neuroimage.2012.05.069. [DOI] [PubMed] [Google Scholar]
- Claassen JAHR, Levine BD, Zhang R. Dynamic cerebral autoregulation during repeated squat-stand maneuvers. J Appl Physiol. 2009;106:153–160. doi: 10.1152/japplphysiol.90822.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Culver JP, Durduran T, Furuya D, Cheung C, Greenberg JH, Yodh AG. Diffuse optical tomography of cerebral blood flow, oxygenation, and metabolism in rat during focal ischemia. J Cereb Blood Flow Metab. 2003;23:911–924. doi: 10.1097/01.WCB.0000076703.71231.BB. [DOI] [PubMed] [Google Scholar]
- Delpy DT, Cope M, van der Zee P, Arridge S, Wray S, Wyatt J. Estimation of optical pathlength through tissue from direct time of flight measurement. Phys Med Biol. 1988;33:1433–1442. doi: 10.1088/0031-9155/33/12/008. [DOI] [PubMed] [Google Scholar]
- Diehl RR, Linden D, Lücke D, Berlit P. Phase relationship between cerebral blood-flow velocity and blood pressure: A clinical test of autoregulation. Stroke. 1995;26:1801–1804. doi: 10.1161/01.str.26.10.1801. [DOI] [PubMed] [Google Scholar]
- Durduran T, Yu G, Burnett MG, Detre JA, Greenberg JH, Wang J, Zhou C, Yodh AG. Diffuse optical measurement of blood flow, blood oxygenation, and metabolism in a human brain during sensorimotor cortex activation. Opt Lett. 2004;29:1766–1768. doi: 10.1364/ol.29.001766. [DOI] [PubMed] [Google Scholar]
- Eames PJ, Potter JF, Panerai RB. Influence of controlled breathing patterns on cerebrovascular autoregulation and cardiac baroreceptor sensitivity. Clin Sci. 2004;106:155–162. doi: 10.1042/CS20030194. [DOI] [PubMed] [Google Scholar]
- Fantini S. Dynamic model for the tissue concentration and oxygen saturation of hemoglobin in relation to blood volume, flow velocity, and oxygen consumption: Implications for functional neuroimaging and coherent hemodynamics spectroscopy (CHS) NeuroImage. doi: 10.1016/j.neuroimage.2013.03.065. this Issue (submitted 2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franceschini MA, Boas DA, Zourabian A, Diamond SG, Nadgir S, Lin DW, Moore JB, Fantini S. Near-Infrared Spiroximetry: Non-Invasive Measurement of Venous Saturation in Piglets and Human Subjects. J Appl Physiol. 2002;92:372–384. doi: 10.1152/jappl.2002.92.1.372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franceschini MA, Joseph DK, Huppert TJ, Diamond SG, Boas DA. Diffuse optical imaging of the whole head. J Biomed Opt. 2006;11:054007. doi: 10.1117/1.2363365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frederiks J, Swenne CA, TenVoorde BJ, Honzikova N, Levert JV, Maan AC, Schalij MJ, Bruschke AV. The importance of high-frequency paced breathing in spectral baroreflex sensitivity assessment. J Hypertens. 2000;18:1635–1644. doi: 10.1097/00004872-200018110-00015. [DOI] [PubMed] [Google Scholar]
- Gabor D. Theory of communication. J Inst Elect Eng (London) 1946;93:429–457. [Google Scholar]
- Hayashi T, Watabe H, Kudomi N, Kim KM, Enmi J-I, Hayashida K, Iida H. A theoretical model of oxygen delivery and metabolism for physiologic interpretation of quantitative cerebral blood flow and metabolic rate of oxygen. J Cereb Blood Flow Metab. 2003;23:1314–1323. doi: 10.1097/01.WCB.0000090506.76664.00. [DOI] [PubMed] [Google Scholar]
- Hyder F, Kida I, Behar KL, Kennan RP, Maciejewski PK, Rothman DL. Quantitative functional imaging of the brain: Towards mapping neuronal activity by BOLD fMRI. NMR Biomed. 2001;14:413–431. doi: 10.1002/nbm.733. [DOI] [PubMed] [Google Scholar]
- Kida I, Rothman DL, Hyder F. Dynamics of changes in blood flow, volume, and oxygenation: implications for dynamic functional magnetic resonance imaging calibration. J Cereb Blood Flow Metab. 2007;27:690–696. doi: 10.1038/sj.jcbfm.9600409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kong Y, Zheng Y, Johnston D, Martindale J, Jones M, Billings S, Mayhew J. A model for the dynamic relationship between blood flow and volume changes during brain activation. J Cereb Blood Flow Metab. 2004;24:1382–1392. doi: 10.1097/01.WCB.0000141500.74439.53. [DOI] [PubMed] [Google Scholar]
- Lang EW, Diehl RR, Mehdorn HM. Cerebral autoregulation testing after aneurysmal subarachnoid hemorrhage: The phase relationship between arterial blood pressure and cerebral blood flow velocity. Crit Care Med. 2001;29:158–163. doi: 10.1097/00003246-200101000-00031. [DOI] [PubMed] [Google Scholar]
- Lee S, Lee M, Koh D, Kim B-M, Choi JH. Cerebral hemodynamic responses to seizure in the mouse brain: simultaneous near-infrared spectroscopy-electroencephalography study. J Biomed Opt. 2010;15:037010. doi: 10.1117/1.3365952. [DOI] [PubMed] [Google Scholar]
- Leung TS, Tachtsidis I, Tisdall MM, Pritchard C, Smith M, Elwell CE. Estimating a modified Grubb’s exponent in healthy human brains with near infrared spectroscopy and transcranial Doppler. Physiol Meas. 2009;30:1–12. doi: 10.1088/0967-3334/30/1/001. [DOI] [PubMed] [Google Scholar]
- Mandeville JB, Marota JJA, Ayata C, Zaharchuk G, Moskowitz MA, Rosen BR, Weisskoff RM. Evidence of a cerebrovascular postarteriole windkessel with delayed compliance. J Cereb Blood Flow Monit. 1999;19:679–689. doi: 10.1097/00004647-199906000-00012. [DOI] [PubMed] [Google Scholar]
- Obata T, Liu TT, Miller KL, Luh W-M, Wong EC, Frank LR, Buxton RB. Discrepancies between BOLD and flow dynamics in primary and supplementary motor areas: application of the balloon model to the interpretation of BOLD transients. NeuroImage. 2004;21:144–153. doi: 10.1016/j.neuroimage.2003.08.040. [DOI] [PubMed] [Google Scholar]
- Obrig H, Neufang M, Wenzel R, Kohl M, Steinbrink J, Einhäupl K, Villringer A. Spontaneous low frequency oscillations of cerebral hemodynamics and metabolism in human adults. NeuroImage. 2000;12:623–639. doi: 10.1006/nimg.2000.0657. [DOI] [PubMed] [Google Scholar]
- Parks T, McClellan J. Chebyshev approximation for nonrecursive digital filters with linear phase. Circuit Theory, IEEE Trans Circuit Theory. 1972;19:189–194. [Google Scholar]
- Payne SJ. A model of the interaction between autoregulation and neural activation in the brain. Math Biosci. 2006;204:260–281. doi: 10.1016/j.mbs.2006.08.006. [DOI] [PubMed] [Google Scholar]
- Phillip D, Schytz HW, Selb J, Payne S, Iversen HK, Skovgaard LT, Boas DA, Ashina M. Low frequency oscillations in cephalic vessels assessed by near infrared spectroscopy. Eur J Clin Invest. 2012;42:1180–1188. doi: 10.1111/j.1365-2362.2012.02704.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pierro M, Sassaroli A, Bergethon PR, Ehrenberg BL, Fantini S. Phase-amplitude investigation of spontaneous low-frequency oscillations of cerebral hemodynamics with near-infrared spectroscopy: A sleep study in human subjects. NeuroImage. 2012;63:1571–1584. doi: 10.1016/j.neuroimage.2012.07.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reinhard M, Müller T, Guschlbauer B, Timmer J, Hetzel A. Transfer function analysis for clinical evaluation of dynamic cerebral autoregulation: a comparison between spontaneous and respiratory-induced oscillations. Physiol Meas. 2003;24:27–43. doi: 10.1088/0967-3334/24/1/303. [DOI] [PubMed] [Google Scholar]
- Reinhard M, Wehrle-Wieland E, Grabiak D, Roth M, Guschlbauer B, Timmer J, Weiller C, Hetzel A. Oscillatory cerebral hemodynamics: The macro- vs. microvascular level. J Neurol Sci. 2006;250:103–109. doi: 10.1016/j.jns.2006.07.011. [DOI] [PubMed] [Google Scholar]
- Sassaroli A, Fantini S. Comment on the modified beer-lambert law for scattering media. Phys Med Biol. 2004;49:N255–N257. doi: 10.1088/0031-9155/49/14/n07. [DOI] [PubMed] [Google Scholar]
- Sassaroli A, Pierro M, Bergethon PR, Fantini S. Low-frequency spontaneous oscillations of cerebral hemodynamics investigated with near-infrared spectroscopy: A review. IEEE J Sel Topics Quant Electron. 2012;18:1478–1492. [Google Scholar]
- Taga G, Konishi Y, Maki A, Tachibana T, Fujiwara M, Koizumi H. Spontaneous Oscillation of oxy- and deoxy-hemoglobin changes with a phase difference throughout the occipital cortex of newborn infants observed using non-invasive optical topography. Neurosci Lett. 2000;282:101–104. doi: 10.1016/s0304-3940(00)00874-0. [DOI] [PubMed] [Google Scholar]
- Tian F, Niu H, Khan B, Alexandrakis G, Behbehani K, Liu H. Enhanced functional brain imaging by using adaptive filtering and a depth compensation algorithm in diffuse optical tomography. IEEE Trans Med Imag. 2011;30:1239–1251. doi: 10.1109/TMI.2011.2111459. [DOI] [PubMed] [Google Scholar]
- Themelis G, D’Arceuil, Diamond SG, Thaker S, Huppert TJ, Boas DA, Franceschini MA. Near-infrared spectroscopy measurement of the pulsatile component of cerebral blood flow and volume from arterial oscillations. J Biomed Opt. 2007;12:014033. doi: 10.1117/1.2710250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zar JH. Biostatistical analysis. 5. Prentice Hall; Upper Saddle River, NJ: 2010. [Google Scholar]
- Zhang R, Zuckerman JH, Giller CA, Levine BD. Transfer function analysis of dynamic cerebral autoregulation in humans. Am J Physiol Heart Circ Physiol. 1998;274:H233–H241. doi: 10.1152/ajpheart.1998.274.1.h233. [DOI] [PubMed] [Google Scholar]
- Zheng F, Sassaroli A, Fantini S. Phasor representation of oxy- and deoxyhemoglobin concentrations: what is the meaning of out-of-phase oscillations as measured by near-infrared spectroscopy? J Biomed Opt. 2010;15:040512. doi: 10.1117/1.3483466. [DOI] [PMC free article] [PubMed] [Google Scholar]


